Kernel methods

Theory and scalable algorithms for kernel-based function approximation.

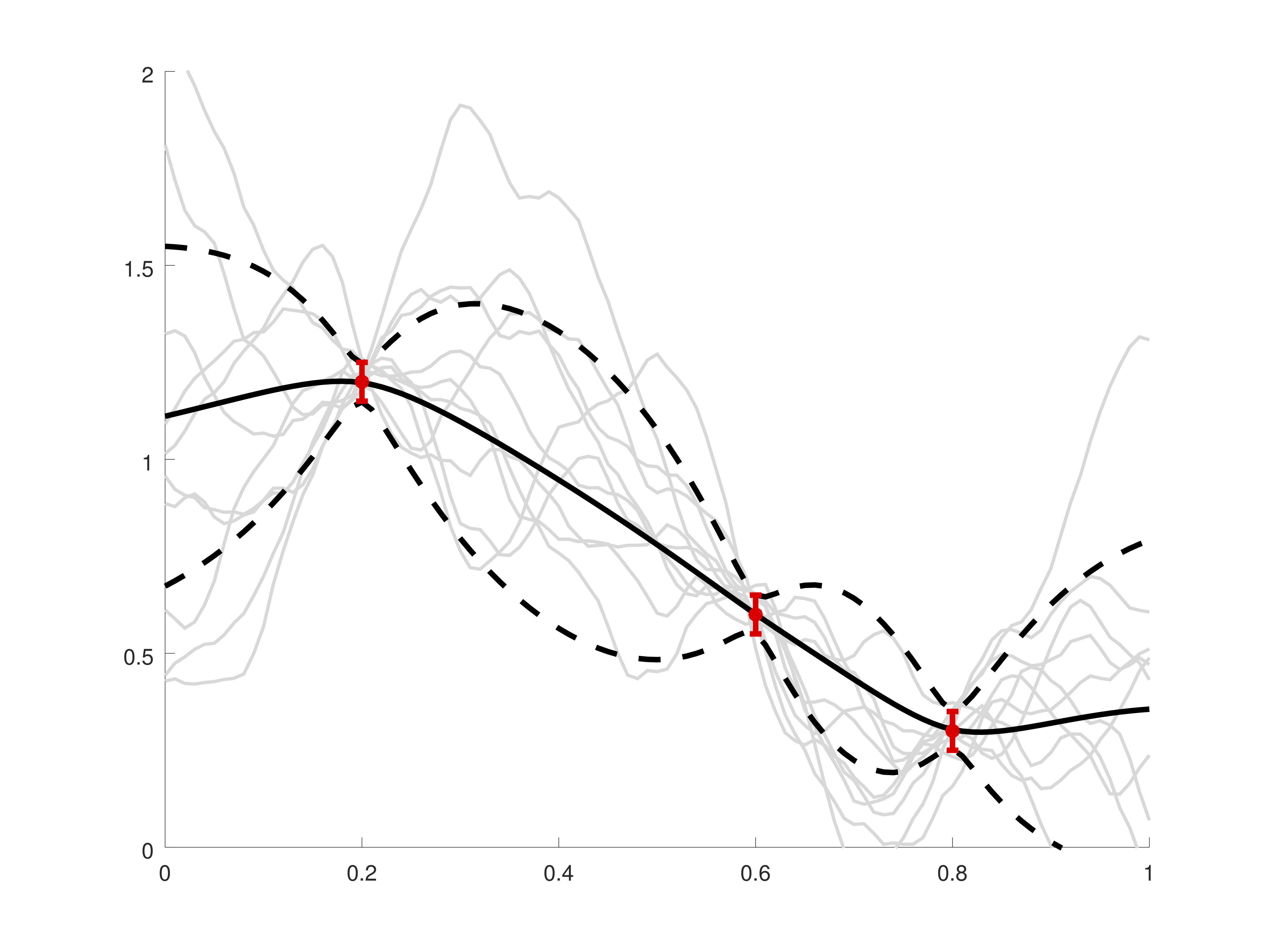
Summary

Kernel methods are a family of methods that involve a function $k(x,y)$ that describes the expected similarity of function values at points $x$ and $y$. These methods are sometimes interpreted probabilistically, with the kernel representing the covariance of random variables at different locations, and sometimes they are interpreted deterministically. These different interpretations provide distinct ways of thinking about kernel selection and error analysis. Independent of the interpretation, kernel methods tend to result in large, dense, highly-structured linear matrix problems; computations with these matrices are a serious bottleneck in scaling to large data sets. In this line of work, we consider both the theoretical aspects of kernel-based function approximation schemes and the nuts-and-bolts of algorithms that exploit matrix structure in order to scale to large data sets.

Related

Parallel surrogate optimization

Asynchronous parallel algorithms for finding minima fast by fitting functions to surrogate models.

Papers

X. Zhu, K. Wu, N. Maus, J. R. Gardner, and D. S. Bindel, “Variational Gaussian Processes with Decoupled Conditionals,” in Advances in Neural Information Processing Systems 2023, 2023. 
@inproceedings{2023-neurips,
  author = {Zhu, Xinran and Wu, Kaiwen and Maus, Natalie and Gardner, Jacob R. and Bindel, David S.},
  title = {Variational Gaussian Processes with Decoupled Conditionals},
  booktitle = {Advances in Neural Information Processing Systems 2023},
  year = {2023},
  month = dec,
  link = {https://openreview.net/forum?id=nwK8UkK3uB}
}

Abstract:

Variational Gaussian processes (GPs) approximate exact GP inference by using a small set of inducing points to form a sparse approximation of the true posterior, with the fidelity of the model increasing with additional inducing points. Although the approximation error in principle can be reduced through the use of more inducing points, this leads to scaling optimization challenges and computational complexity. To achieve scalability, inducing point methods typically introduce conditional independencies and then approximations to the training and test conditional distributions. In this paper, we consider an alternative approach to modifying the training and test conditionals, in which we make them more flexible. In particular, we investigate decoupling the parametric form of the predictive mean and covariance in the conditionals, and learn independent parameters for predictive mean and covariance. We derive new evidence lower bounds (ELBO) under these more flexible conditionals, and provide two concrete examples of applying the decoupled conditionals. Empirically, we find this additional flexibility leads to improved model performance on a variety of regression tasks and Bayesian optimization (BO) applications.

X. Zhu, L. Huang, E. H. Lee, C. A. Ibrahim, and D. Bindel, “Bayesian Transformed Gaussian Processes,” Transactions on Machine Learning Research, 2023. 
@article{2023-tmlr,
  title = {Bayesian Transformed Gaussian Processes},
  author = {Zhu, Xinran and Huang, Leo and Lee, Eric Hans and Ibrahim, Cameron Alexander and Bindel, David},
  journal = {Transactions on Machine Learning Research},
  issn = {2835-8856},
  year = {2023},
  link = {https://openreview.net/forum?id=4zCgjqjzAv},
  arxiv = {2210.10973}
}

Abstract:

The Bayesian transformed Gaussian (BTG) model, proposed by Kedem and Oliviera in 1997, was developed as a Bayesian approach to trans-Kriging in the spatial statistics community. In this paper, we revisit BTG in the context of modern Gaussian process literature by framing it as a fully Bayesian counterpart to the Warped Gaussian process that marginalizes out a joint prior over input warping and kernel hyperparameters. As with any other fully Bayesian approach, this treatment introduces prohibitively expensive computational overhead; unsurprisingly, the BTG posterior predictive distribution, itself estimated through high-dimensional integration, must be inverted in order to perform model prediction. To address these challenges, we introduce principled numerical techniques for computing with BTG efficiently using a combination of doubly sparse quadrature rules, tight quantile bounds, and rank-one matrix algebra to enable both fast model prediction and model selection. These efficient methods allow us to compute with higher-dimensional datasets and apply BTG with layered transformations that greatly improve its expressibility. We demonstrate that BTG achieves superior empirical performance over MLE-based models in the low-data regime —situations in which MLE tends to overfit.

X. Zhu, J. Gardner, and D. Bindel, “Efficient Variational Gaussian Processes Initialization via Kernel-based Least Squares Fitting,” in Proceedings of NeurIPS 2022 Workshop on Gaussian Processes, Spatiotemporal Modeling, and Decision-making Systems, 2022. 
@inproceedings{2022-neurips,
  author = {Zhu, Xinran and Gardner, Jacob and Bindel, David},
  title = {Efficient Variational {Gaussian} Processes Initialization via Kernel-based Least Squares Fitting},
  month = dec,
  year = {2022},
  booktitle = {Proceedings of NeurIPS 2022 Workshop on Gaussian Processes, Spatiotemporal Modeling, and Decision-making Systems},
  link = {https://gp-seminar-series.github.io/neurips-2022/assets/camera_ready/35.pdf}
}

Abstract:

Stochastic variational Gaussian processes (SVGP) scale Gaussian process inference to large datasets through inducing points and stochastic training. However, the training process involves hard multimodal optimization, and often suffers from slow and suboptimal convergence when initializing inducing points directly from training data. We provide a better initialization of inducing points from kernelbased least squares fitting. We show empirically that our approach consistently reaches better prediction performance. The total time cost of our method, including initialization, is comparable to the standard SVGP training.

X. Zhu, Y. Liu, P. Ghysels, D. Bindel, and X. S. Li, “GPTuneBand: Multi-task and Multi-fidelity Autotuning for Large-scale High Performance Computing Applications,” in Proceedings of the SIAM Conference on Parallel Processing, 2022. 
@inproceedings{2022-siam-pp,
  author = {Zhu, Xinran and Liu, Yang and Ghysels, Pieter and Bindel, David and Li, Xiaoye S.},
  title = {{GPTuneBand}: Multi-task and Multi-fidelity Autotuning for Large-scale High Performance Computing Applications},
  booktitle = {Proceedings of the SIAM Conference on Parallel Processing},
  month = feb,
  year = {2022},
  link = {https://crd.lbl.gov/assets/Uploads/GPTuneBand.pdf}
}

Abstract:

This work proposes a novel multi-task and multi-fidelity autotuning framework, GPTuneBand, for tuning large-scale expensive high performance computing (HPC) applications. GPTuneBand combines a multi-task Bayesian optimization algorithm with a multi-armed bandit strategy, well-suited for tuning expensive HPC applications such as numerical libraries, scientific simulation codes and machine learning (ML) models, particularly with a very limited tuning budget. Our numerical results show that compared to other stateof-the-art autotuners, which only allows single-task or single-fidelity tuning, GPTuneBand obtains significantly better performance for numerical libraries and simulation codes, and competitive validation accuracy for training ML models. When tuning the Hypre library with 12 parameters, GPTuneBand wins over its single-fidelity predecessor GPTune on 62.5% tasks, with a maximum speedup of 1.2x, and wins over a single-task, multi-fidelity tuner BOHB on 72.5% tasks. When tuning the MFEM library on large numbers of CPU cores, GPTuneBand obtains a 1.7x speedup when compared with the default code parameters.

M. Padidar, X. Zhu, L. Huang, J. Gardner, and D. Bindel, “Scaling Gaussian Processes with Derivative Information Using Variational Inference,” in Proceedings of NeurIPS 2021, 2021. 
@inproceedings{2021-neurips,
  author = {Padidar, Misha and Zhu, Xinran and Huang, Leo and Gardner, Jacob and Bindel, David},
  title = {Scaling {Gaussian} Processes with Derivative Information Using Variational Inference},
  month = dec,
  year = {2021},
  booktitle = {Proceedings of NeurIPS 2021},
  link = {https://proceedings.neurips.cc/paper/2021/file/32bbf7b2bc4ed14eb1e9c2580056a989-Paper.pdf}
}

Abstract:

Gaussian processes with derivative information are useful in many settings where derivative information is available, including numerous Bayesian optimization and regression tasks that arise in the natural sciences. Incorporating derivative observations, however, comes with a dominating $O(N^3 D^3)$ computational cost when training on $N$ points in $D$ input dimensions. This is intractable for even moderately sized problems. While recent work has addressed this intractability in the low-$D$ setting, the high-$N$, high-$D$ setting is still unexplored and of great value, particularly as machine learning problems increasingly become high dimensional. In this paper, we introduce methods to achieve fully scalable Gaussian process regression with derivatives using variational inference. Analogous to the use of inducing values to sparsify the labels of a training set, we introduce the concept of inducing directional derivatives to sparsify the partial derivative information of a training set. This enables us to construct a variational posterior that incorporates derivative information but whose size depends neither on the full dataset size $N$ nor the full dimensionality $D$. We demonstrate the full scalability of our approach on a variety of tasks, ranging from a high dimensional stellarator fusion regression task to training graph convolutional neural networks on Pubmed using Bayesian optimization. Surprisingly, we find that our approach can improve regression performance even in settings where only label data is available.

I. Delbridge, D. Bindel, and A. G. Wilson, “Randomly projected additive Gaussian processes for regression,” in Proceedings of Machine Learning and Systems 2020, 2020, pp. 7526–7536. 
@inproceedings{2020-icml,
  author = {Delbridge, Ian and Bindel, David and Wilson, Andrew Gordon},
  title = {Randomly projected additive {Gaussian} processes for regression},
  booktitle = {Proceedings of Machine Learning and Systems 2020},
  pages = {7526--7536},
  year = {2020},
  link = {https://proceedings.icml.cc/static/paper_files/icml/2020/4272-Paper.pdf},
  talk = {https://icml.cc/virtual/2020/poster/6248}
}

Abstract:

Gaussian processes (GPs) provide flexible distributions over functions, with inductive biases controlled by a kernel. However, in many applications Gaussian processes can struggle with even moderate input dimensionality. Learning a low dimensional projection can help alleviate this curse of dimensionality, but introduces many trainable hyperparameters, which can be cumbersome, especially in the small data regime. We use additive sums of kernels for GP regression, where each kernel operates on a different random projection of its inputs. Surprisingly, we find that as the number of random projections increases, the predictive performance of this approach quickly converges to the performance of a kernel operating on the original full dimensional inputs, over a wide range of data sets, even if we are projecting into a single dimension. As a consequence, many problems can remarkably be reduced to one dimensional input spaces, without learning a transformation. We prove this convergence and its rate, and additionally propose a deterministic approach that converges more quickly than purely random projections. Moreover, we demonstrate our approach can achieve faster inference and improved predictive accuracy for high-dimensional inputs compared to kernels in the original input space.

D. Eriksson, K. Dong, E. Lee, D. Bindel, and A. G. Wilson, “Scaling Gaussian Process Regression with Derivatives,” in Proceedings of NeurIPS 2018, 2018. 
@inproceedings{2018-nips-a,
  author = {Eriksson, David and Dong, Kun and Lee, Eric and Bindel, David and Wilson, Andrew Gordon},
  title = {Scaling {Gaussian} Process Regression with Derivatives},
  booktitle = {Proceedings of NeurIPS 2018},
  month = dec,
  year = {2018},
  arxiv = {1810.12283.pdf},
  link = {http://papers.nips.cc/paper/7919-scaling-gaussian-process-regression-with-derivatives}
}

Abstract:

Gaussian processes (GPs) with derivatives are useful in many applications, including Bayesian optimization, implicit surface reconstruction, and terrain reconstruction. Fitting a GP to function values and derivatives at $n$ points in $d$ dimensions requires linear solves and log determinants with an $n(d + 1) × n(d + 1)$ positive definite matrix – leading to prohibitive $O(n^3 d^3)$ computations for standard direct methods. We propose iterative solvers using fast $O(nd)$ matrix-vector multiplications (MVMs), together with pivoted Cholesky preconditioning that cuts the iterations to convergence by several orders of magnitude, allowing for fast kernel learning and prediction. Our approaches, together with dimensionality reduction, enables Bayesian optimization with derivatives to scale to high-dimensional problems and large evaluation budgets.

J. Gardner, G. Pleiss, K. Weinberger, D. Bindel, and A. G. Wilson, “GPyTorch: Blackbox Matrix-Matrix Gaussian Process Inference with GPU Acceleration,” in Proceedings of NeuroIPS 2018, 2018. 
@inproceedings{2018-nips-b,
  author = {Gardner, Jacob and Pleiss, Geoff and Weinberger, Killian and Bindel, David and Wilson, Andrew Gordon},
  title = {{GPyTorch}: Blackbox Matrix-Matrix {Gaussian} Process Inference with {GPU} Acceleration},
  booktitle = {Proceedings of NeuroIPS 2018},
  month = dec,
  year = {2018},
  arxiv = {1809.11165.pdf},
  link = {http://papers.nips.cc/paper/7985-gpytorch-blackbox-matrix-matrix-gaussian-process-inference-with-gpu-acceleration}
}

Abstract:

Despite advances in scalable models, the inference tools used for Gaussian processes (GPs) have yet to fully capitalize on developments in computing hardware. We present an efficient and general approach to GP inference based on Blackbox Matrix-Matrix multiplication (BBMM). BBMM inference uses a modified batched version of the conjugate gradients algorithm to derive all terms for training and inference in a single call. BBMM reduces the asymptotic complexity of exact GP inference from $O(n^3)$ to $O(n^2)$. Adapting this algorithm to scalable approximations and complex GP models simply requires a routine for efficient matrix-matrix multiplication with the kernel and its derivative. In addition, BBMM uses a specialized preconditioner to substantially speed up convergence. In experiments we show that BBMM effectively uses GPU hardware to dramatically accelerate both exact GP inference and scalable approximations. Additionally, we provide GPyTorch, a software platform for scalable GP inference via BBMM, built on PyTorch.

K. Dong, D. Eriksson, H. Nickisch, D. Bindel, and A. G. Wilson, “Scalable Log Determinants for Gaussian Process Kernel Learning,” in Proceedings of NIPS 2017, 2017. 
@inproceedings{2017-nips,
  author = {Dong, Kun and Eriksson, David and Nickisch, Hannes and Bindel, David and Wilson, Andrew Gordon},
  booktitle = {Proceedings of NIPS 2017},
  title = {Scalable Log Determinants for Gaussian Process Kernel Learning},
  year = {2017},
  month = dec,
  link = {https://arxiv.org/pdf/1711.03481.pdf},
  arxiv = {1711.03481.pdf}
}

Abstract:

For applications as varied as Bayesian neural networks, determinantal point processes, elliptical graphical models, and kernel learning for Gaussian processes (GPs), one must compute a log determinant of an $n \times n$ positive definite matrix, and its derivatives – leading to prohibitive $O(n^3)$ computations. We propose novel $O(n)$ approaches to estimating these quantities from only fast matrix vector multiplications (MVMs). These stochastic approximations are based on Chebyshev, Lanczos, and surrogate models, and converge quickly even for kernel matrices that have challenging spectra. We leverage these approximations to develop a scalable Gaussian process approach to kernel learning. We find that Lanczos is generally superior to Chebyshev for kernel learning, and that a surrogate approach can be highly efficient and accurate with popular kernels.

Talks

Inducing Point Approximations of Kernel Matrices

SIAM Annual Meeting 2022, Pittsburgh (hybrid)
kernel • meeting minisymposium external invited

Chebyshev Featurization

Householder Symposium XXI, Selva di Fasano
kernel • poster meeting external invited

Inducing Point Approximations of Kernel Matrices

eNLA seminar, online
kernel • seminar external invited

New Approaches to Computing with Kernels

Chelluri lecture, Cornell math colloquium series
kernel • colloquium invited

Structured Numerical Linear Algebra for Gaussian Process Modeling

SIAM Applied Linear Algebra 2021, online
gp kernel • meeting plenary external invited

Stochastic Linear Algebra for Scalable Gaussian Processes

Applied Mathematics Colloquium, Illinois Institute of Technology
gp kernel • colloquium external invited

Stochastic Linear Algebra for Scalable Gaussian Processes

CAM Colloquium, University of Chicago
gp kernel • colloquium external invited

Stochastic Linear Algebra for Scalable Gaussian Processes

IEMS Seminar, Northwestern University
gp kernel • seminar external invited

LA Support for Scalable Kernel Methods

Workshop on Approximation Theory and Machine Learning, Purdue
gp kernel • meeting external invited

Stochastic LA for Scaling GPs

International Workshop on Computational Math, Suzhou
gp kernel • meeting external invited

Scalable Algorithms for Kernel-Based Surrogates in Prediction and Optimization

Workshop on Surrogate Models and Coarsening Techniques, UCLA IPAM
gp kernel • meeting external invited

Stochastic LA for Scaling GPs

Cornell SCAN seminar
gp kernel • seminar local

Stochastic estimators in Gaussian process kernel learning

Householder Symposium
gp kernel • meeting external invited poster

RBF Response Surfaces with Inequality Constraints

SIAM CSE
rbf • minisymposium external organizer

Radial Basis Function Interpolation with Bound Constraints

Cornell SCAN Seminar
rbf • seminar local