Getting Started
Amazon EcoVistas is a graphical user interface for visualizing the Pareto-optimal frontier of proposed Amazon hydropower projects with respect to total energy capacity and a collection of a five environmental criteria—river connectivity, sediment transport, degree of regulation, fish biodiversity threat, and greenhouse gas emissions. For more details, see the paper:
Alexander S. Flecker, Qinru Shi, Rafael M. Almeida, Héctor Angarita, Jonathan M. Gomes-Selman, Roosevelt García-Villacorta, Suresh A. Sethi, Steven A. Thomas, N. LeRoy Poff, Bruce R. Forsberg, Sebastian A. Heilpern, Stephen K. Hamilton, Jorge D. Abad, Elizabeth P. Anderson, Nathan Barros, Isabel Carolina Bernal, Richard Bernstein, Carlos M. Cañas, Olivier Dangles, Andrea C. Encalada, Ayan S. Fleischmann, Michael Goulding, Jonathan Higgins, Céline Jezequel, Erin I. Larson, Peter B. McIntyre, John M. Melack, Mariana Montoya, Thierry Oberdorff, Rodrigo Paiva, Guillaume Perez, Brendan H. Rappazzo, Scott Steinschneider, Sandra Torres, Mariana Varese, M. Todd Walter, Xiaojian Wu, Yexiang Xue, Xavier E. Zapata-Ríos, Carla P. Gomes (2022). Reducing adverse impacts of Amazon hydropower expansion. Science, 375(6582): 753–760. https://doi.org/10.1126/science.abj4017
Pareto frontiers in the context of hydropower and strategic river basin planning
Strategic basin planning aims at maximizing benefits (e.g., hydropower production) while minimizing costs (e.g., socioenvironmental disruption). Considering these objectives is a difficult balancing act that inherently requires the evaluation of trade-offs among multiple—and often competing—objectives. The Pareto frontier represents a clear picture for analyzing and navigating these trade-offs in objective optimization.
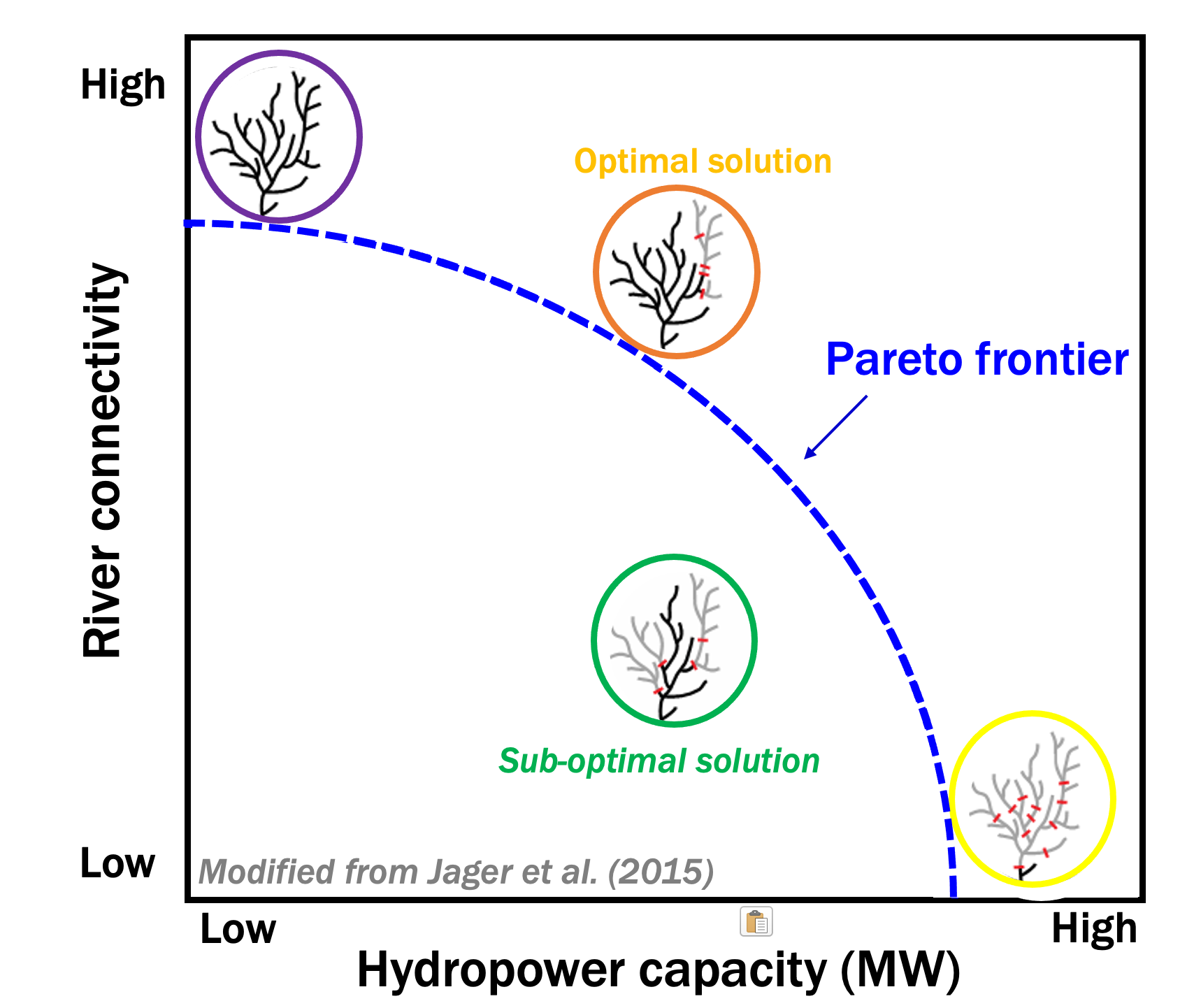
River network connectivity serves as an especially good metric for illustrating the Pareto-optimal frontier in the context of hydropower planning. Low river connectivity indicates that the river basin is highly fragmented by dams, which affects species migrations, navigation, and the movement of materials such as sediments; conversely, high connectivity indicates greater ecological integrity by maintaining a multitude of free-flowing rivers. In this conceptual diagram the horizontal axis represents hydropower installed capacity and the vertical axis represents river connectivity for different spatial configurations of dams in a river network. In the figure below, colored circles represent different river networks affected by hypothetical portfolios or build-outs of dams.
The purple circle on the top left shows a Pareto-optimal scenario with no dams built in the basin, resulting in no hydropower generation but a fully connected river network (i.e., high river connectivity). Conversely, on the opposite end, the yellow circle shows a Pareto-optimal scenario where all possible hypothetical dams have been built across the basin; thus, hydropower yield is at the highest possible value, yet little connectivity remains. Between these two extremes, there are many possible Pareto-optimal portfolios of dams (or “solutions”) that consider both objectives simultaneously. In other words, as one slides from right to left along the x-axis, the dashed blue line plots optimal dam configurations with the highest amount of connectivity for different hydropower generation targets. A Pareto-optimal solution is a portfolio of dams that is not outperformed—or dominated—by any other solution (portfolio of dams) with respect to every objective considered. In this hypothetical example, there are no solutions above the blue line, whereas the space below the blue line is full of sub-optimal solutions. For any given sub-optimal solution there exists at least one dominating solution that provides at least the same amount of energy with lower connectivity disruption—or conversely, at most the same amount of connectivity disruption with higher energy generation. The orange and green circles illustrate a Pareto-optimal and a sub-optimal solution respectively; both have the same hydropower installed capacity, but the top solution (orange) dominates the bottom solution (green) because it allows a larger fraction of the river network to remain free-flowing.
The example above considers only two objectives; however, we can frame much more complex multi-objective optimization problems by considering three or more objectives. In the context of our Amazon dams project, we work with six objectives—hydropower, river connectivity, sediment transport, degree of regulation, fish biodiversity threat, and greenhouse gas emissions. For example, if two solutions both provide 30 GW of installed capacity and have the same value in connectivity, degree of regulation, fish biodiversity, and greenhouse gas emissions, but solution A traps more river sediments than solution B, then solution B dominates solution A (i.e., because sediment is a criterion to be maximized). Conversely, if solution A provides 40 GW of installed capacity and solution B provides 30 GW of installed capacity, and the values of all other criteria remain unchanged, then solution A and B do not dominate each other.
More formally, we define a solution π (also referred to as a portfolio) as a subset of proposed dams that could potentially be built in the Amazon river basin. For a total of d objectives, we denote their values as z1(π), z2(π), …, zd(π). In the following example, we assume that all objectives are non-negative and are to be maximized, where objective functions that are to be minimized (e.g., greenhouse gas emissions, fish biodiversity threat, and degree of regulation) can be treated similarly. Given two solutions π and π', if for every objective i, zi(π) ≥ zi(π') and strict inequality holds for at least one objective, we consider that solution π dominates π'.
Computing the Pareto frontier
Computing the full Pareto frontier for a multi-objective optimization problem is a non-deterministic polynomial-time hard (NP-hard) problem, meaning that the runtime could be exponential in the number of dams in the worst case. Given the large number of proposed (n=351) and existing (n=158) Amazon dams (n=509 total) and possible dam combinations (2509, or 10153), computing the exact Pareto frontier for multiple criteria is intractable. Thus, our algorithm finds a set of solutions that approximate the Pareto frontier. Given two solutions π and π', we say that π ε-dominates π', if and only if, (1+ε) zi(π) ≥ zi(π') for every objective i. For a Pareto-optimal frontier P and a solution set P', we say that P' ε-approximates P, if and only if, for every Pareto-optimal solution π in P, there exists a solution π' in P' such that π' ε-dominates π. Finding an ε-approximation of a Pareto-optimal frontier for a fixed number of criteria can be solved in polynomial time, and we developed an efficient algorithm for it. See details in the paper.
Visualizing the multidimensional Pareto frontier with Amazon EcoVistas
Visualizing and understanding the Pareto frontier is in itself a major challenge. Given the inherent difficulty of visualizing high-dimensional spaces, simultaneously considering three or more criteria further adds great complexity to interpreting Pareto optimization outcomes. The task is further compounded by the fact that our methodology has the power to generate the unconstrained Pareto frontier for the full range of the different criteria at a fine grain, which typically translates into a vast number of Pareto-optimal solutions with diverse tradeoffs. So, for a gentle introduction to the Pareto frontier, we provide 2D Pareto frontiers, i.e., only considering two criteria at a time (hydropower and one environmental criterion). 2D Pareto frontiers are easier for humans to visualize and understand. Nevertheless, while 2D Pareto frontiers are user-friendly, they misrepresent our framework’s high-dimensional capabilities of truly reasoning and optimizing the Pareto frontier at much higher dimensions. Therefore, we also developed 6D parallel plot representations to capture the Pareto frontier considering all criteria simultaneously, with the capability to constrain the range for each criterion, eliminating solutions outside the selected ranges.
Map of dam locations
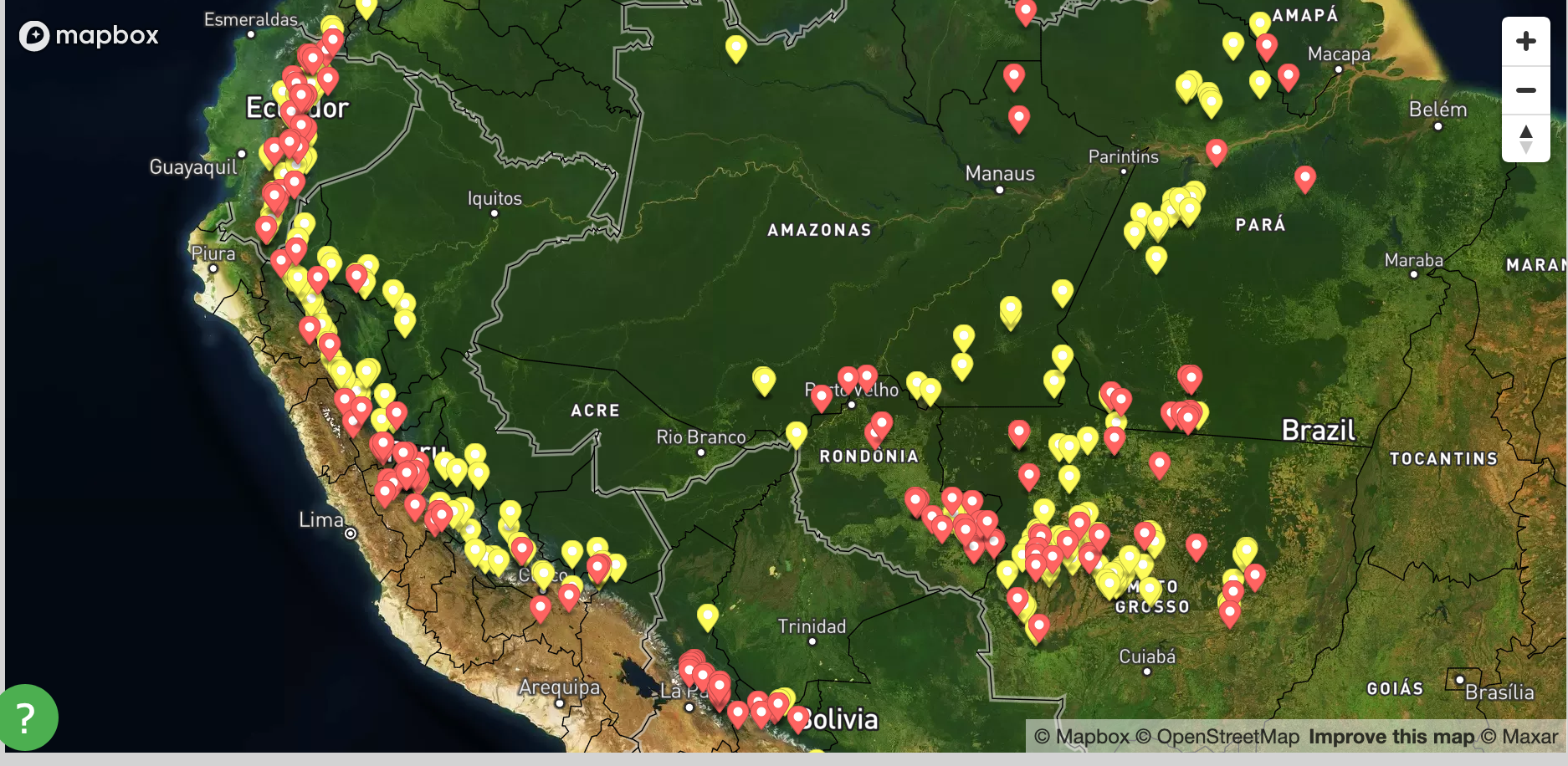
The interactive map shows the locations of dams in a given solution selected by clicking a specific point (yellow star) in the 2D scatter plots. The red dots represent the existing dams, and the yellow dots represent the proposed dams. The user can use the map toggles feature to display only existing or proposed dams, or both. By clicking on a specific dam pin, the user can see basic attribute data such as dam name, country, and installed capacity.
2D Pareto Frontier (single)
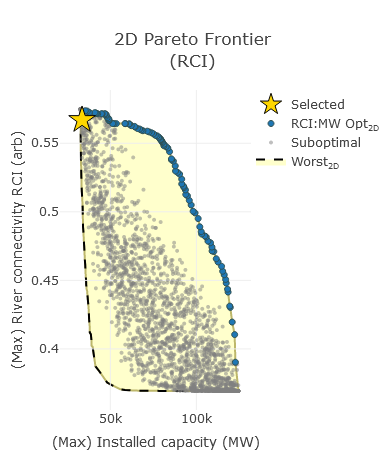
This plot illustrates an example of a 2D Pareto frontier with respect to two criteria: river connectivity (RCI) and hydropower installed capacity. Both criteria should be maximized. The Pareto frontier is given by the blue dotted curve. The plot also shows randomly sampled suboptimal (or dominated) solutions as gray dots and the worst possible 2D solutions as the black dashed line. To obtain more information on a specific solution, users can click on the solution in any 2D scatter plot to visualize its dams on the interactive map at the top of the page. The selected solution will also be automatically shown as a star in other 2D plots, with corresponding values for the other environmental criteria.
2D Pareto Frontier (compared)
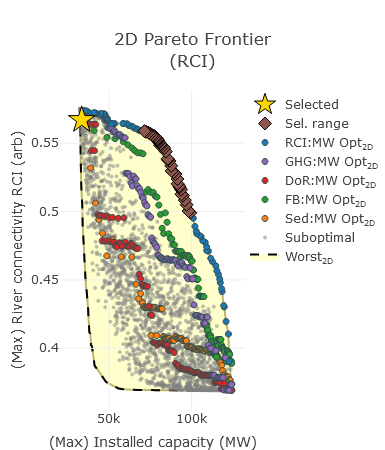
This plot illustrates an example of a 2D Pareto frontier optimized for energy and an environmental criterion and its comparisons with 2D Pareto frontiers optimized for energy and each of the other environmental criteria. In the example shown, aside from the blue dots that show the 2D Pareto frontier for river connectivity index (RCI) and installed capacity, which are the same as in 2D Pareto Frontier (single), the plot also provides comparisons in terms of RCI values with the solutions optimized for installed capacity and one of the other criteria. For example, the red dots represent the RCI outcomes of the Pareto frontier optimized for only energy and degree of regulation (DoR), and the purple dots represent the RCI outcomes of the Pareto frontier optimized for only installed capacity and greenhouse gas emissions (GHG). The plot also shows the selected range of solutions with brown diamonds. The selection of a range for a given criterion is made via the 6D parallel plot.
6D Pareto Frontiers
Given the inherent limitations of human cognition for visualizing high-dimensional spaces, Amazon EcoVistas is particularly helpful for navigating the 6D Pareto frontier and the multiple tradeoffs between hydropower capacity and the five environmental criteria. In the 6D mode, the user can constrain desired ranges for each criterion in a parallel coordinate plot, eliminating solutions outside of selected ranges. The user can also obtain more in-depth information and view the Pareto frontier from multiple perspectives through the 2D projections.
2D projection of a 6D Pareto Frontier

This plot illustrates an example of a 6D Pareto frontier plotted as a 2D projection with respect to two criteria: river connectivity (RCI) and installed capacity. The plot is not very intuitive because it is a 2D representation of a 6D space. Although similar in format, this plot is quite different from the 2D Pareto frontier plots because the displayed optimal solutions result from the optimization that considers all six criteria simultaneously. In particular, while some of the 6D Pareto optimal solutions are along the edge of the 2D plot (resembling the standard 2D Pareto frontier), other 6D Pareto-optimal solutions are interior solutions and, therefore, they seem to violate the notion of Pareto frontier. Nevertheless, these seemingly sub-optimal solutions are, in fact, Pareto-optimal solutions when considering all six criteria because the other criteria not shown in the plot make up for the optimality. In other words, though when only considering the two criteria (in this case, RCI and installed capacity), some solutions seem to be dominated dominated by others, they are optimal when considering all the six criteria.
The plot also shows the selected range of solutions with magenta diamonds. The selection of a range for a given criterion is made via the parallel plot described below.
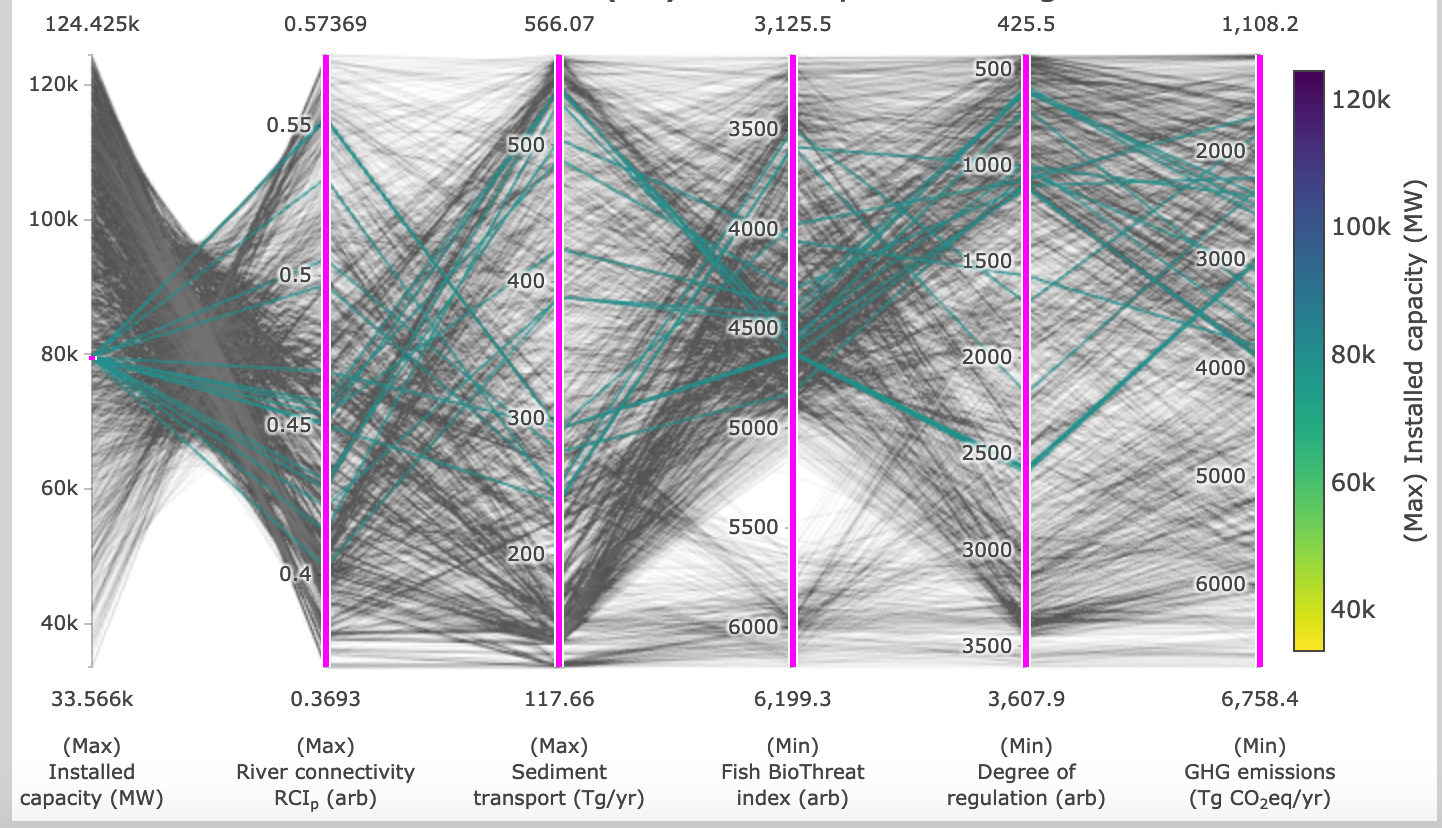
6D parallel coordinate plot
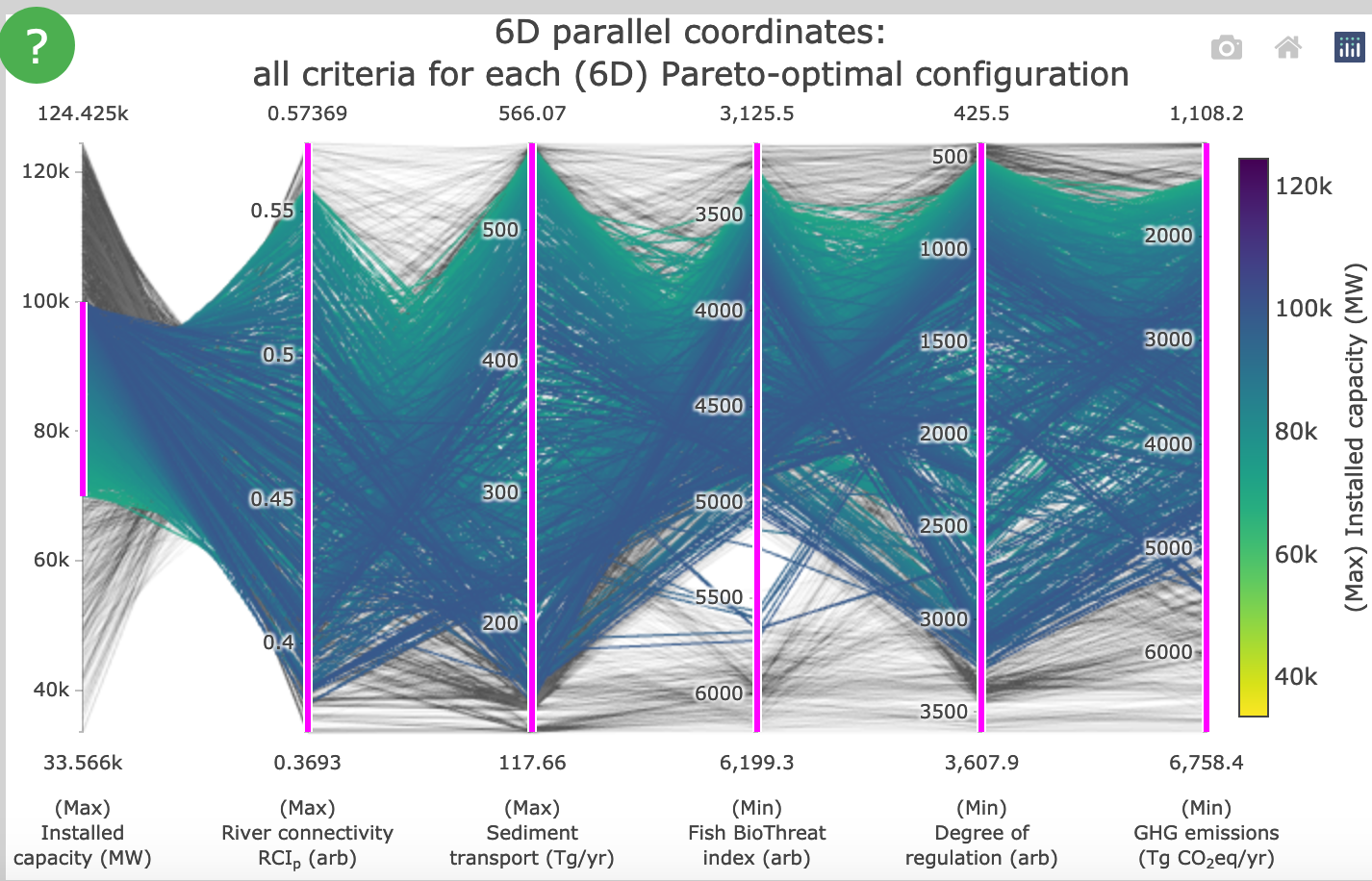
In the parallel coordinate plot, each parallel coordinate corresponds to a criterion, and each zigzag line connecting different values on the coordinates corresponds to a single Pareto-optimal solution. The user can constrain desired ranges for each criterion in the parallel coordinate plot, eliminating solutions outside of selected ranges and thus significantly reducing the number of solutions to be considered. The selected solutions are then displayed on the 2D projections as diamonds. To obtain more information on a specific solution, the user can click on the solution in any 2D scatter plot to visualize its dams on the interactive map at the top of the page. The selected solution will also be automatically shown as a star in other 2D projections.