CS465 Fall 2003 Homework 2

CS465 Homework 2

This homework has separate handouts for the written part:

and the programming part:

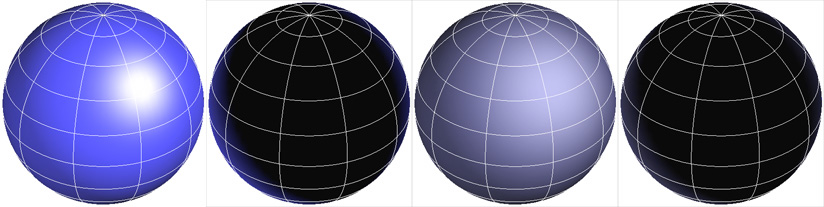
hw2b assignment handout | framework code
solution text | (solution code on CMS)

Some reasonable parameter values (used in images below):

spheroid: s_x = s_z = 1; s_y = 0.5
graph: s_x = s_z = 3; s_y = 0.5; s_r = 18; sigma = 0.3
torus: r_o = 1; r_i = 0.3
helicoid: s_y = 2; r = 1; n = 2
cruller: r_o = 1; r_i = 0.3; n = 3; m = 1; a = 0.2

Using the framework

To help make it easier for you to compile the framework in your favorite IDE, we have eliminated all packages from the code, so that all the .java files sit in a single directory.

You still need the support libraries. The documentation for the support libraries can be found here. Unlike the brush assignment, this assignment does depend on the vecmath library.

Implementation hints

There are some hints we've given to some people, so I'll post them here.

For the function graph: the square map is a good place to start.
For the torus: think about cylindrical coordinates.
For the rippled torus: really, you are just adding a more complicated definition for r_i.
If you set the normals to zero, you will get consistently black shading.
Here are images of a sphere rendered in the framework with (1) normals facing outward and surface oriented outward, (2) normals facing inward and surface oriented outward, (3) normals facing inward and surface oriented inward, and (4) normals facing outward and surface oriented inward.
The moral of the story is that shading works when the surface orientation agrees with the normals, showing you shiny blue on the front and dull gray-blue on the back, and shading breaks when the orientation and normals disagree.

Generally, when you're evaluating a complicated expression and also keeping track of its derivative, you should break the function evaluation down into manageable steps, giving names to the intermediate results. Then you can also compute the derivatives in the same steps, computing the derivatives of the intermediate results and using them in the chain rule down the line. This is vastly easier to debug than one huge formula that could have a typo anywhere.

For instance, suppose I want to evaluate sin(cos^2(sin(x)) + exp(x^3)). I could write out the whole derivative in one step, like this:

y = sin(cos^2(sin(x)) + exp(x^3)) dy_dx = cos(cos(sin(x))^2 + exp(x^3)) * (3 * exp(x^3) * x^2 - 2 * cos(sin(x)) * sin(sin(x)) * cos(x))

but I had to resort to Mathematica before I got that right. On the other hand I could rewrite the formula in steps, like this:

a = cos(sin(x)) da_dx = -sin(sin(x)) * cos(x) b = exp(x^3) db_dx = exp(x^3) * (3 * x^2) y = sin(a^2 + b) dy_dx = cos(a^2 + b) * (2 * a * da_dx + db_dx)

and this one is easy to verify by reading it through step by step.

Helpful pictures

Here are pictures of all the maps (with unspecified cameras) to help you understand what the surfaces are supposed to look like.

Cornell CS465 Fall 2003 (cs465-staff@cs.cornell.edu)