| Index |
| How our Iterative Search Algorithm Works |
| Other Applications of our Algorithm |
Our Model
First, all of the bonds must be length one, all of the bond angles must be 120 degrees (for example), and no two monomers can be overlapping. All of these constraints define positive energies, whose sum must go to zero. This condition is called the polymer constraint.
Second, the hydrophobic monomers are affected by an attractive potential, and the hydrophillic monomers are not attracted to any other monomers. This hydrophobic-hydrophobic attraction defines a negative energy, that must get below a certain pre-specified cutoff. This condition is called the monomer constraint.
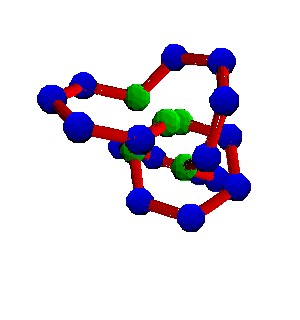
Here is a picture of a protein satisfying both the monomer and the polymer constraint. Notice all the bonds lengths are one, all of the bond angles are 120 degrees (in this example), and no two spheres are overlapping.
Notice also that the hydrophobic monomers (the green spheres) are close together, so the attractive potential energy is quite negative.
If one works within the polymer constraint (hard spheres with fixed bond angles and lengths), and simply does gradient descent with the above attractive potential, the protein will fold itself into a stable configuration with an energy significantly above the lowest energy possible, or the "ground state". The ground state corresponds to the "native fold" of the protein, to use biology terms. Finding the ground state in our model is very challenging, and a simplification of one of the central problems in computational biology: that of predicting the folded form of a real protein starting from it's sequence of amino acids.
movie of misfolding.
This protein is moving under the attractive hydrophobic-hydrophobic potential, within the polymer constraint. A local minimum in the energy is found, but this is not the global minimum. Notice while the proteins energy is decreasing, no bond length ever deviates from 1, no bong angle ever deviates from 120 degrees, and no two spheres ever overlap.
Our iterative search algorithm finds the ground state by searching for a folded form whose energy is below a certain specified amount. In this way, all misfolded forms whose energy are above the specified energy are ignored, and never found.
The iterate is a collection of monomer coordinates, or a potential protein. The succesive iterates are only functions of the previous iterates. In this manner, as the algorithm proceeds, the iterate jumps all over protein configuration space. It could be said that the iterate is acted upon by a dynamical system defined by the various energies mentioned above.
The remarkable thing about our algorithm, is that the iterate evolves, it rarely satisfies either constraint. The searching algorithm moves outside of both constraints, so energy barriers are avoided.
movie of proper folding.
As this protein evolves, each iterate satisfies neither constraint, until it gets close to a solution, at which point the iterate finds a fixed point.