| Home |
| How The Difference Map Works |
| Other Applications of the Difference Map |
Other Applications of the Difference Map
1. Phase retrieval
A complete review of the problem can be found here .
There are several related problems that are all called phase retrieval, but basically the problem is to find an object satisfying given Fourier modulus data. For example, imagine Alice has a secret binary vector, which she Fourier transforms, and gives Bob the Fourier component amplitudes (but keeps the phases secret). Can Bob find a binary vector whose Fourier modulii match Alices?
2. The knapsack problem
This is a very old problem, with a rich and interesting history. A brief review can be found here
Imagine Alice once again has a 20 long secret binary vector. There is a public list of 20 numbers, for example,
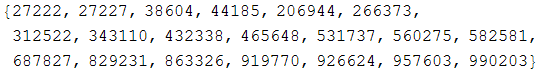 .
.Alice finds the dot product of her vector and this list, and it turns out to be 5958254.
Can you find out Alices secret binary vector? The answer is here .
3. Finding Ramsey numbers
Imagine 5 points in a plane, with every point connected with a line segment to every other point. There are thus 10 line segments. Can you color all these line segments with two colors so no solid-color-triangle is made? This is not too hard, a solution is given here .
Now try the same thing with 6 dots, 15 lines, and 2 colors. Don't try too long, it can't be done.
How about 3 colors? 6 dots, 15 lines, and 3 colors is easy to color so no solid-color-triangle is made. With 3 colors, additional dots can be added to about 15 total. With 14 dots, 91 lines, the difference map found this. Notice there is no solid-color-trangles in the entire picture!
15 dots, 105 lines, and 3 colors can be done, but it is very hard. 16 dots, 120 lines, and 3 colors is impossible. There will always be a solid-color-triangle
How about 4 colors? It can be shown that 65 dots, 2080 lines, and 4 colors is impossible, but how about 60 dots? Nobody knows if 60 dots, 1770 lines, and 4 colors can be done. It is certainly very difficult.