How our Iterative Search Algorithm Works

The Algorithm

Often the solution to a difficult problem can be represented as the intersection of two constraint spaces. In the context of the protein model outlined on the main page, the two constraint spaces are:

Constraint 1 --- Have all the bond lengths and bond angles correct, and have no spheres overlapping
Constraint 2 --- Have the attractive hydrophobic-hydrophobic energy below a specified amount

Assume for a moment you have a collection of monomers that satisfy neither constraint. It is relatively easy to minimally move the monomers so contraint 1 is satisfied, or to minimally move the monomers so contraint 2 is satisifed, but trying to satisfy both at the same time is very difficult. This is the purpose of the iterative search algorithm.

So if a problem can be phrased as searching for the intersection of two contraint spaces, and distance minimizing projections can be efficiently computed for these constraint spaces, then the iterative search algorithm will find their intersection fairly quickly.
A distance minimizing projection is defined as follows: given an collection of monomers (an iterate) that does not satisfy a constraint, find the smallest change to the position of the monomers so that the iterate does satisfy the constraint. The "smallest change" is that which minimizes the sum of euclidian distances moved by all the monomers.

In the context of protein folding, these projections are defined as follows:
For Constraint 1, Define an energy,

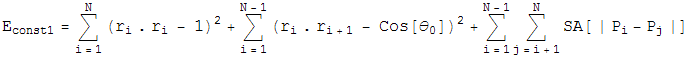
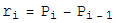
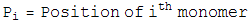
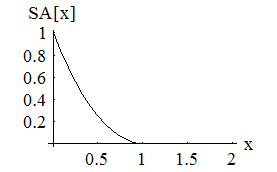
which is the sum of the bond lenth and bond angle constraints, and the self avoiding energy whose functional form is plotted. We simpliy let this energy be minimized by a greedy energy minimization scheme. All three energy terms go to zero for a protein satisfying constraint 1, so we let this energy be minimized until the total energy is sufficiently close to zero. In practice, these three energy terms are mild enough that frustration is not a problem.

For Constraint 2, Define an energy,

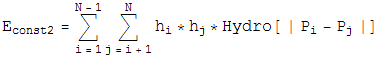
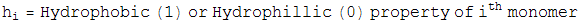
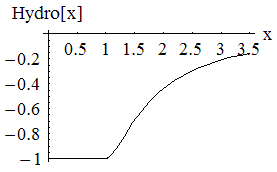
which is the attractive hydrophobic-hydrophobic interaction energy. Notice if a monomer is hyrdophillic, h=0, so the monomer contributes no energy to this sum. The only energies come from two hydrophobic balls, and the interaction energy is plotted. We also let this energy be minimized by a greedy energy minimization scheme. Since during this minimization, the bond length is allowed to vary from 1 unit, and the bond angle is allowed to be different from the specified amount, the minimization is not frustrated, and almost always finds the global minimum.

Once the two projections for the two constraint spaces have been worked out, the iterative search algorithm is defined in terms of these projections as:

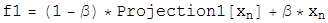
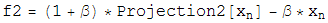
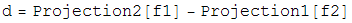
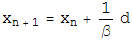
Beta is a dimensionless parameter that specifies the relative strength of the two contraints, that is, the optimum value for beta depends on how much work each projection on average does.
Notice that if d=0, then the iterate no longer evolves, a fixed point has been found. Notice also that if d=0, a point that lives on the first constraint space, P1(F2), is the same as a point on the second constraint space, P2(f1). So a point living on both constraint spaces has been found! Notice finally that the iterate will continue evolving utill this happens. There are no other fixed points except for the solution.

The various plus and minus signs in the above equation have been worked out so the solution is an attractive fixed point, and near-solutions are NOT fixed points.