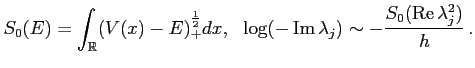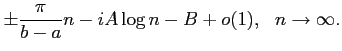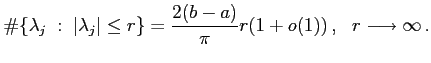Resonances and phase space geometry
![\includegraphics[width=16cm]{spl.eps}](img151.gif)
|
In this section we will give a qualitative description of
geometric origins of various types of resonances. This is
based on semiclassical analysis of the correspondence
between the phase space dynamics and the behaviour of
solutions of
![]() .
.
The phase space for problems in one dimensional scattering
is given by
![]() :
:
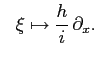
Here we will simply put ![]() and take a potential which is large
enough to exhibit some qualitative semiclassical phenomena. It is a
and take a potential which is large
enough to exhibit some qualitative semiclassical phenomena. It is a
![]() potential given in Fig.3. By an energy level we
mean the set
potential given in Fig.3. By an energy level we
mean the set
![\includegraphics[width=16cm]{rebd.eps}](img164.gif)
|
The bound states, that is solutions of
![]() ,
with
,
with
![]() ,
, ![]() , are well approximated by
WKB methods using Bohr-Sommerfeld rules - see [20]. That
correspondence is shown in colour in Fig.4.
, are well approximated by
WKB methods using Bohr-Sommerfeld rules - see [20]. That
correspondence is shown in colour in Fig.4.
![\includegraphics[width=16cm]{shre.eps}](img168.gif)
|
The closed components of energy levels ![]() with
with ![]() cannot
support bound states since
cannot
support bound states since ![]() cannot have positive eigenvalues.
However, they support shape resonances. The real parts are
semiclassically close to the energy levels given by Bohr-Sommerfeld rules,
while the imaginary parts are approximated using the tunneling distance
also known as the Agmon distance:
cannot have positive eigenvalues.
However, they support shape resonances. The real parts are
semiclassically close to the energy levels given by Bohr-Sommerfeld rules,
while the imaginary parts are approximated using the tunneling distance
also known as the Agmon distance:
In our example
|
|
|
| 7.9363 | 7.3281 |
| 3.7500 | 2.2884 |
![\includegraphics[width=16cm]{rehs.eps}](img174.gif)
|
It will be interesting to compare the more precise results of [13, Sect.10] with numerical results. For the moment, we show another example obtained using the following code (see Fig.6):
x = [-2.5,-2,-1,-0,75,-0.5,0,0.5,0.75,1,2,2.5] V = [0,0.2,[1,0.5625,0.25,0,0.25,0,0,5625,1]+0.1,0.2,0] splinepot(36*V,2*x)
![\includegraphics[width=16cm]{btre.eps}](img176.gif)
|
Fig.7 focuses on the barrier top resonances generated
by the two unstable equilibria. Semiclassicaly, a potential, ![]() , with a
nondegenerate global maximum at
, with a
nondegenerate global maximum at ![]() has resonances approximately given by
has resonances approximately given by
provided some other conditions are satisfied - see [6]. In Fig.7 we see that a nearly degenerate resonances are generated by the two ``barrier tops'' - they correspond to
![\includegraphics[width=16cm]{reck.eps}](img181.gif)
|
In Fig.8 we show a computation for a ![]() approximation
of the Eckart barrier potential,
approximation
of the Eckart barrier potential,
![]() . In that case
resonances are given exactly by
. In that case
resonances are given exactly by
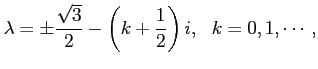
![\includegraphics[width=16cm]{rere.eps}](img186.gif)
|
In Fig.9 we show resonances with larger real parts. They dominate large energy asymptotics of resonances and are generated by the reflection by the singularities at the end points of the support of the potential. This heuristic analysis is known to be correct if the potential behaves as follows
The resonances then have the following asymptotic form
We will call them Regge resonances (as opposed to related but different Regge poles) since such asymptotic formulæ origin in the work of Tullio Regge [27]. For simple potentials satisfying (27) (see Fig.1), asymptotics (28) are visible almost immediately but for complicated potentials, large energies are necessary - see Fig.2 and Fig.10.
As was also observed by Regge, (28) gives a counting law for resonances
For arbitrary potentials (which may not satisfy (27)), (29) was proved in [34], and different new proofs were provided in [11] and [29].
![\includegraphics[width=16cm]{repa.eps}](img190.gif)
|
David Bindel 2006-10-04