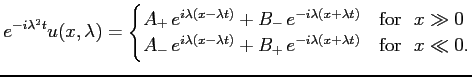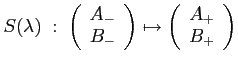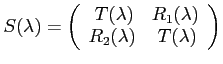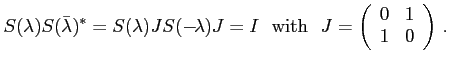Resonances as poles of the scattering matrix
We first have to define the scattering matrix. For that we will take a quantum mechanical point of view and consider the time dependent Schrödinger equation,
If
For
The scattering matrix is defined to be the operator which maps the incoming coefficients to the outgoing coefficients, that is
The matrix
![]() is meromorphic for
is meromorphic for
![]() where poles with
where poles with
![]() correspond to the square root
of the eigenvalues of
correspond to the square root
of the eigenvalues of ![]() . Its poles in the lower half plane
coincide with resonances.
. Its poles in the lower half plane
coincide with resonances.
The coefficients in
are the transmission,
We have the following general properties of
![]()
Since on the real axis
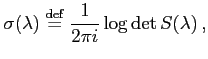
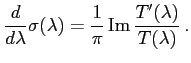
where for simplicity we assumed that there is no resonance at
The convergence is guaranteed by the following consequence of Carleman's formula (see [34]):
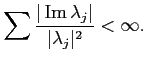
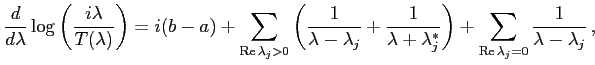
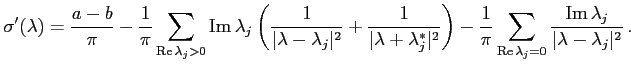
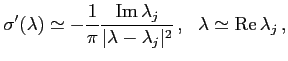
In particular, high energy behaviour of
![]() is
given by
is
given by
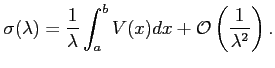
David Bindel 2006-10-04