Introduction

The simplest model of scattering/quantum resonances comes from considering compactly supported potentials on the real line,

$$V(x) \in \mathbb{R}, \vert V(x)\vert \leq C, V(x) = 0 \vert x\vert > L ,$$ (1)

and the corresponding Schrödinger operator,

$$H_V \stackrel{\rm {def}}{=}- \partial_x^2 + V(x).$$ (2)

The mathematical definition of resonances is simple and elegant: they are the poles of the resolvent/Green's function continued meromorphically from the physical half-plane to the lower/non-physical half plane. More precisely, consider the resolvent

$$R_V(\lambda) \stackrel{\rm {def}}{=}(H_V - \lambda^2)^{-1} \; : \... ...longrightarrow L^2(\mathbb{R}) , \ \mathop{\rm Im}\nolimits \lambda > 0,$$

(with poles at $\lambda$ for which $\lambda^2$ is an eigenvalues of $H_V$ - see §4). This operator is essentially the same as the outgoing Green's function, $G_V(\lambda, x, y)$:

$$R_V(\lambda) \varphi(x) = \int_\mathbb{R}G_V(\lambda, x, y) \varphi(y) dy.$$

The convention about outgoing/incoming is the choice of analyticity of $R_V(\lambda)$ and $G_V(\lambda)$ in $\pm \mathop{\rm Im}\nolimits \lambda > 0$.

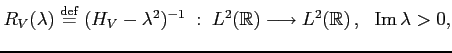
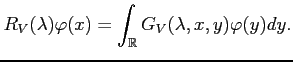
For fixed $x$ and $y$ the Green's function has a meromorphic continuation from $\mathop{\rm Im}\nolimits \lambda > 0$ to $\mathbb{C}$. That is essentially equivalent to the fact that

$$R_V(\lambda) \;:\; L^2_{\rm {comp}}(\mathbb{R}) \rightarrow L^2_{\rm {loc}}(\mathbb{R}),$$

has a meromorphic continuation. Note that we shrank the domain to a smaller space of $L^2$ functions vanishing outside a bounded set, $L^2_{\rm comp}$, and enlarged the range to a larger space of functions which are square integrable on bounded intervals only, $L^2_{\rm {loc}}$.

Resonances are now defined as poles of the meromorphic continuation of Green's function $G_V(\lambda)$, or equivalently of the resolvent, $R_V(\lambda)$. Since

$$R_V(\lambda) = R_V(-\bar \lambda)^*, \mathop{\rm Im}\nolimits \lambda > 0,$$

the same relation holds in $\mathbb{C}$, and resonances are symmetric with respect to the imaginary axis. Figure 1 is an example how they look for a simple potential.

Figure 1: Resonances of a square well potential computed with squarepot([0,-4,0],[-2,-1,1,2]).

This definition although very elegant is not very intuitive. Resonances manifest themselves very concretely in wave expansions, peaks of the scattering cross sections, and phase shift transitions. In §4 we will describe the wave expansion interpretation.

There are many conflicting conventions in the subject partly due to its independent emergence in different branches of science and mathematics. The convention above comes from electromagnetic/sound scattering where $\lambda$ is a frequency. In that context resonances are often called scattering poles. In quantum mechanics $\lambda^2$ rather than $\lambda$ would be called a resonance. In automorphic scattering, or scattering on hyperbolic manifolds of dimension $n + 1$, the convention names $s$ for which $s (n - s) = \lambda^2 + n^2/2$ to be resonances. In the context of black holes, resonances are called quasi-normal modes.

For a general account of resonances in one dimensional scattering we suggest [32]. Perhaps the first study of the distribution of resonances/scattering poles was conducted by Regge [27], though his motivation was very different. For mathematical results in one dimension see [1],[11],[14],[18],[24],[29],[34], and many other articles.

A lighthearted sketch of the general theory is provided in [35], while for a proper introduction and many references one should consult [30]. The expansion of solutions of the wave equation in terms of scattering poles was emphasized early by Lax and Phillips - see [25]. In fact, these expansions explained in §4 have even been used to compute scattering poles numerically [21]. For a broader context of geometric scattering theory [23] is a nice introduction.