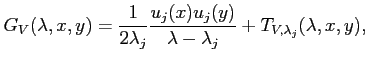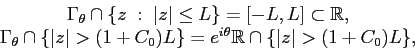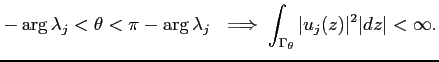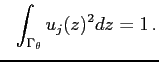How to normalize resonant states?
What is not provided in (11) is a formula for the coefficients
![]() (the formulæ for
(the formulæ for ![]() 's an
's an ![]() 's are the same as in
(6)). If
's are the same as in
(6)). If ![]() is a resonant state then the
assumption of compact support on initial data in (7) shows
that the integrals
is a resonant state then the
assumption of compact support on initial data in (7) shows
that the integrals
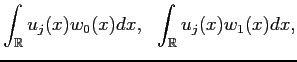
One possibility is to use the Lax-Phillips semigroup, ![]() -
see [25],[23], and also [31] for a concise treatment in a
very general setting. The semigroup
-
see [25],[23], and also [31] for a concise treatment in a
very general setting. The semigroup ![]() not only provides the most elegant
way of defining resonances, but is in fact the only purely dynamical
definition: resonances are simply the eigenvalues of its generator.
However, it is perhaps the beauty of this definition that makes its
applicability limited (even in one dimension some modifications have to
be made [22]). It is also rather cumbersome numerically.
not only provides the most elegant
way of defining resonances, but is in fact the only purely dynamical
definition: resonances are simply the eigenvalues of its generator.
However, it is perhaps the beauty of this definition that makes its
applicability limited (even in one dimension some modifications have to
be made [22]). It is also rather cumbersome numerically.
Instead, let us go back to Green's function,
Near a simple pole, that is near a simple resonance,
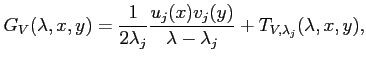
with the resonant state
Suppose for simplicity that
![]() in the initial
value problem (7). Then in the expansion (11)
we can choose the resonant functions to be given by
in the initial
value problem (7). Then in the expansion (11)
we can choose the resonant functions to be given by ![]() 's
and we have
's
and we have
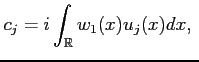 with the resonant state with the resonant state |
(15) |
That provides a preferred choice of a resonant state but not a normalization.
To find a normalization of ![]() we observe that (9)
and (10) shows that we can continue
we observe that (9)
and (10) shows that we can continue ![]() analytically to
analytically to
for some
It turns out that the normalization which determines ![]() in
(14) and (15) is
in
(14) and (15) is
Contour deformation shows that this condition is independent of the choice of
We cannot fully explain the origin of the normalization given in (18). It comes from the celebrated complex scaling method discovered by Aguilar-Combes and Balslev-Combes in the early 70s, and greatly developed in mathematics, computational physics, and chemistry - see [30] and [35] for a discussion and references.
Roughly speaking, we can restrict the operator ![]() to the
contour
to the
contour
![]() . It then acts (as an unbounded
operator) on
. It then acts (as an unbounded
operator) on
![]() rather than
rather than
![]() .
The resonances with
.
The resonances with
![]() are the eigenvalues of this
new non-self-adjoint operator, denoted by
are the eigenvalues of this
new non-self-adjoint operator, denoted by
![]() .
Its resolvent,
.
Its resolvent,
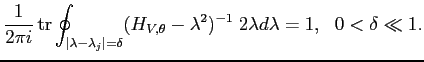
David Bindel 2006-10-04