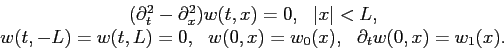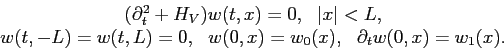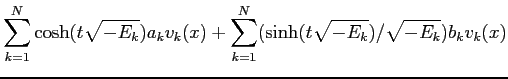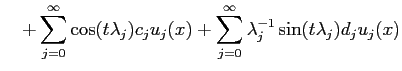Eigenvalues of Schrödinger operators on bounded intervals
Before explaining how resonances defined in §1 are related to
the long time behaviour of scattered waves we discuss the more familiar
case of eigenvalues and eigenfuctions.
The displacement, ![]() , of a point
, of a point ![]() on vibrating string,
on vibrating string,
![]() , at time
, at time ![]() , is approximately given by the solution of
the wave equation:
, is approximately given by the solution of
the wave equation:
We can generalize this by introducing a potential and considering the wave equation for a Schrödinger operator,
The Dirichlet (zero boundary condition) realization of the operator
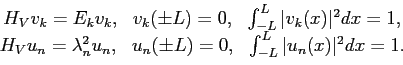
where
This decomposition is the basis of harmonic analysis, signal processing, and many other things.
David Bindel 2006-10-04