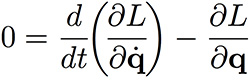
• V.I. Arnold, Mathematical Methods of Classical Mechanics, Springer, 2nd edition, 1989. (more mathematical text)
  
• H. Goldstein et al., Classical Mechanics, Addison Wesley, 3rd edition, 2001. (standard ugrad physics text)
  
• S.T. Thornton and J.B. Marion, Classical Dynamics of Particles and Systems, Brooks Cole, 5th edition, 2003. (easier ugrad physics text)
  

• N-body problems (all-pairs complexity)
• Reduced-coordinate deformable bodies (spatial/integration complexity)
• 2D serial manipulator (recursive complexity)

Read for next class:

• Rotational and rigid motion;  kinematics and dynamics
  
• SO(3), Special Orthogonal group in 3D
• SE(3), Special Euclidean group in 3D
• Rigid-body motion
• Spatial velocity vectors (contravariant twists);  se(3); transformation
  
• Kinetic energy; inertia, principal axes
  
• Spatial forces (covariant wrenches); se*(3); transformation
• Velocity of contact points, and relation to twists
  
• Forces at contact points, and relation to wrenches
• Newton-Euler equations of motion
• Integrating rigid-body dynamics
• Deformable bodies;  mode matrix, U;  extensions to framework
  

• David Baraff and Andrew Witkin, Physically Based Modeling, Online SIGGRAPH 2001 Course Notes, 2001.
• Rigid Body Simulation (slides)
  

• Murray, R. M., Sastry, S. S., and Zexiang, Li, A Mathematical Introduction to Robotic Manipulation. 1st. CRC Press, Inc., 1994.
• See summary in appendix of: 
  
• Danny M. Kaufman, Timothy Edmunds and Dinesh K. Pai, Fast Frictional Dynamics for Rigid Bodies, ACM Transactions on Graphics (SIGGRAPH 2005), 24(3), August 2005.
• Ball's screw theory
• Ahmed A. Shabana, Dynamics of Multibody Systems, Cambridge, 3rd ed, 2005.

• Roy Featherstone and David Orin, Robot Dynamics: Equations and Algorithms, Proc. IEEE Int. Conf. Robotics & Automation, San Francisco, CA, 2000, pp. 826–834. (an excellent review)

• Algorithms overview
• Forward and inverse kinematics
  
• Inverse dynamics (control)
  
• Forward dynamics (simulation)
• Notation
• Recurrence relations
• Recursive Newton-Euler Algorithm (RNEA)
• O(N) inverse dynamics
• Composite-Rigid-Body Algorithm (CRBA)
• O(n^2)  mass matrix 
  
• Usage in O(N^3) forward dynamics (CRBA + RNEA + dense solve)
• Articulated-Body Algorithm (ABA)
• a.k.a. "Featherstone's algorithm"
• O(N) forward dynamics
• Closed-loop systems
• Constraints and fast solution methods
  
• Global analysis techniques
• Fast robot algorithms as sparse matrix methods

• Roy Featherstone and David Orin, Robot Dynamics: Equations and Algorithms, Proc. IEEE Int. Conf. Robotics & Automation, San Francisco, CA, 2000, pp. 826–834. (an excellent review)
  
• Roy Featherstone, Robot Dynamics Algorithms, Kluwer Academic Publishers, 1987. (classic book--highly readable)
• Roy Featherstone, A Divide-and-Conquer Articulated-Body Algorithm for Parallel O(log(n)) Calculation of Rigid-Body Dynamics. Part 1: Basic Algorithm, The International Journal of Robotics Research, Vol. 18, No. 9, 867-875, 1999.  (has good appendix on spatial notation)
  
• Roy Featherstone, Rigid Body Dynamics Algorithms, Boston: Springer, 2007.
• E. Kokkevis, Practical Physics for Articulated Characters, Proc. of Game Developers Conference (GDC), 2004. (good overview of system integration issues for ABA, e.g., handling contact and constraints)
  
• David Baraff, Linear-Time Dynamics using Lagrange Multipliers, Proceedings of SIGGRAPH 96, Computer Graphics Proceedings, Annual Conference Series, August 1996, pp. 137-146.
• Robot dynamics, Scholarpedia page.
  
• D.K. Pai, STRANDS: Interactive Simulation of Thin Solids using Cosserat Models, Computer Graphics Forum, 21(3), pp. 347-352, 2002.

• James Melfi leads discussion of
• E. Kokkevis, Practical Physics for Articulated Characters, Proc. of Game Developers Conference (GDC), 2004.
• Submit comments before class to Piazza forum.

Topics discussed:

• Elastic rods, and recursive algorithm for evaluation of quasistatic stress, strain and configuration
• D.K. Pai, STRANDS: Interactive Simulation of Thin Solids using Cosserat Models, Computer Graphics Forum, 21(3), pp. 347-352, 2002.
• Miklós Bergou, Max Wardetzky, Stephen Robinson, Basile Audoly, Eitan Grinspun, "Discrete Elastic Rods," ACM Transactions on Graphics (SIGGRAPH) 2008.
  

• Deniz Gunceler leads discussion of 

Kiran S. Bhat, Steven M. Seitz, Jovan Popovic & Pradeep K. Khosla, Computing the Physical Parameters of Rigid-body Motion from Video, ECCV 2002. Submit comments before class to Piazza forum.

Topics discussed:

• Miklós Bergou, Max Wardetzky, Stephen Robinson, Basile Audoly, Eitan Grinspun, "Discrete Elastic Rods," ACM Transactions on Graphics (SIGGRAPH) 2008.

• Patrick Berens leads discussion of
  
• Matthias Müller, Nuttapong Chentanez, Tae-Yong Kim, Real time dynamic fracture with volumetric approximate convex decompositions. ACM Trans. Graph. 32(4): 115 (2013)  
• Submit comments before class to Piazza forum.

Relevant Papers:

• Demetri Terzopoulos, Kurt Fleischer, Modeling Inelastic Deformation: Viscoelasticity, Plasticity, Fracture, Computer Graphics (Proceedings of SIGGRAPH 88), August 1988, pp. 269-278.
  
• James F. O'Brien, Jessica K. Hodgins, Graphical Modeling and Animation of Brittle Fracture, Proceedings of SIGGRAPH 99, Computer Graphics Proceedings, Annual Conference Series, August 1999, pp. 137-146.
• James F. O'Brien, Adam W. Bargteil, Jessica K. Hodgins, Graphical Modeling and Animation of Ductile Fracture, ACM Transactions on Graphics, 21(3), July 2002, pp. 291-294.
• Neil Molino, Zhaosheng Bao, Ron Fedkiw, A virtual node algorithm for changing mesh topology during simulation, ACM Transactions on Graphics, 23(3), August 2004, pp. 385-392.
  
• M. Müller, M. Gross, Interactive Virtual Materials, in Proceedings of Graphics Interface (GI 2004), pp 239-246, London, Ontario, Canada, May 17-19, 2004. (Video)
  
• Mark Pauly, Richard Keiser, Bart Adams, Philip Dutré, Markus Gross, Leonidas J. Guibas, Meshless animation of fracturing solids, ACM Transactions on Graphics, 24(3), August 2005, pp. 957-964. (Video)
  
• Hayley N. Iben, James F. O'Brien, Generating Surface Crack Patterns, 2006 ACM SIGGRAPH / Eurographics Symposium on Computer Animation, September 2006, pp. 177-186.
• Denis Steinemann, Miguel A. Otaduy, Markus Gross, Fast Arbitrary Splitting of Deforming Objects, 2006 ACM SIGGRAPH / Eurographics Symposium on Computer Animation, September 2006, pp. 63-72. (Video)
  
• Bao, Z., Hong, J.-M., Teran, J. and Fedkiw, R., Fracturing Rigid Materials, IEEE TVCG 13, 370-378 (2007).
  
• Eftychios Sifakis, Kevin G. Der, Ronald Fedkiw, Arbitrary Cutting of Deformable Tetrahedralized Objects, 2007 ACM SIGGRAPH / Eurographics Symposium on Computer Animation, August 2007, pp. 73-80.
• Eric G. Parker and James F. O'Brien, Real-Time Deformation and Fracture in a Game Environment, In Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation, pages 156–166, August 2009.
• Su, J., Schroeder, C. and Fedkiw, R., Energy Stability and Fracture for Frame Rate Rigid Body Simulations, ACM SIGGRAPH/Eurographics Symposium on Computer Animation (SCA), edited by Eitan Grinspun and Jessica Hodgins, pp. 155-164 (2009).
  
• Changxi Zheng, Doug L. James, Rigid-Body Fracture Sound with Precomputed Soundbanks, ACM Transactions on Graphics, 29(4), July 2010, pp. 69:1-69:13.

• Please use the template found here (LaTeX) or similar style.
  
• Submit your proposal (in PDF format) via CMS.
• Submit anytime -- CMS deadline (Oct 31)
• Work alone or in pairs.
• Please talk with me about possible project ideas, or for feedback.

• Yining Karl Li leads discussion of
  
• K. Museth, “VDB: High-Resolution Sparse Volumes With Dynamic Topology”. ACM Transactions on Graphics, Volume 32, Issue 3, Pages 27:1-27:22, June 2013. [PDF]
  
• Submit comments before class to Piazza forum.
• Eston Schweickart leads discussion of
  
• Reconstructing Surfaces of Particle-Based Fluids Using Anisotropic Kernels   Jihun Yu (Industrial Light and Magic), Greg Turk (Georgia Institute of Technology)
• Submit comments before class to Piazza forum.

Topics discussed: On handling holonomic constraints for elastic rods in the first programming assignment:

• Holonomic constraints
• Constrained Lagrangian Dynamics (CLD)
  
• Constraint projection methods
• (More details on constrained systems in a future lecture)
• References:
• U.M. Ascher and L.R. Petzold, Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations, SIAM.
• David Baraff and Andrew Witkin, Physically Based Modeling, Online SIGGRAPH 2001 Course Notes, 2001.
• Constrained Dynamics (slides)
• Examples from Cloth Simulation:
• Rony Goldenthal, David Harmon, Raanan Fattal, Michel Bercovier, Eitan Grinspun, Efficient Simulation of Inextensible Cloth, ACM Transactions on Graphics, 26(3), July 2007, pp. 49:1-49:7.  [ACM Digital Library link]
• Jonathan M. Kaldor, Doug L. James, Steve Marschner, Simulating Knitted Cloth at the Yarn Level, ACM Transactions on Graphics, 27(3), August 2008, pp. 65:1-65:9.

• Daniel Knowlton leads discussion of
  
• MultiFLIP for Energetic Two-Phase Fluid Simulation    
  Landon Boyd, Robert Bridson (University of British Columbia)
• Submit comments before class to Piazza forum.

• Advection;  upwind differencing;  ENO schemes
• Incompressibility constraint
• Navier-Stokes equation
• MAC grid discretization;  interpolation and averaging;  upwinding
  
• Time-stepping schemes (Eulerian, and semi-Lagrangian)
• Projection to divergence-free velocity
  
• Poisson equation; discretization;  compatibility condition;  PCG solution
  
• DAE view of incompressible flow
• Higher-order semi-Lagrangian schemes;  monotone interpolation;  BFECC;  CIP and USCIP
  

• S. Osher and R. Fedkiw, Level Set Methods and Dynamic Implicit Surfaces, Applied Mathematical Sciences, volume 153, Springer-Verlag, 2003.
  
• U.M. Ascher and L.R. Petzold, Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations, SIAM.
• Jos Stam, Stable Fluids, Proceedings of SIGGRAPH 99, Computer Graphics Proceedings, Annual Conference Series, August 1999, pp. 121-128.
  
• Slides and notes
• Ronald Fedkiw, Jos Stam, Henrik Wann Jensen, Visual Simulation of Smoke, Proceedings of ACM SIGGRAPH 2001, Computer Graphics Proceedings, Annual Conference Series, August 2001, pp. 15-22.  (introduces vorticity confinement forces)
• Bridson, R., Fedkiw, R., and Muller-Fischer, M. 2006. Fluid simulation: SIGGRAPH 2006 course notes, In ACM SIGGRAPH 2006 Courses (Boston, Massachusetts, July 30 - August 03, 2006). SIGGRAPH '06. ACM Press, New York, NY, 1-87.  [Slides]
• 2007 course [ACM Digital Library Link --- with video of presentations]
  
• Foster, N. and Fedkiw, R., Practical Animation of Liquids, SIGGRAPH 2001, 15-22 (2001).
• Enright, D., Marschner, S. and Fedkiw, R., Animation and Rendering of Complex Water Surfaces, SIGGRAPH 2002, ACM TOG 21, 736-744 (2002).
• Yongning Zhu , Robert Bridson, Animating sand as a fluid, ACM Transactions on Graphics (TOG), v.24 n.3, July 2005. (Discusses PIC and FLIP hybrid particle/grid methods)
• Higher-order advection schemes: 
• BFECC and MacCormack methods: 
  
• Byungmoon Kim, Yingjie Liu, Ignacio Llamas, Jarek Rossignac,
  Advections with Significantly Reduced Dissipation and Diffusion, IEEE Transactions on Visualization and Computer Graphics, Volume 13, Issue 1, Pages 135-144, 2007. video(DivX)
• Selle, A., Fedkiw, R., Kim, B., Liu, Y., and Rossignac, J. 2008. An Unconditionally Stable MacCormack Method. J. Sci. Comput. 35, 2-3 (Jun. 2008), 350-371.
  
• Methods with small stencils (constrained interpolation profile (CIP)):
• Doyub Kim, Oh-young Song, Hyeong-Seok Ko, A Semi-Lagrangian CIP Fluid Solver without Dimensional Splitting, Computer Graphics Forum, 27(2), April 2008, pp. 467-475. (project page with videos)
• A projection method to approximate complex boundaries:
• Jeroen Molemaker, Jonathan M. Cohen, Sanjit Patel, Jun-yong Noh. Low Viscosity Flow Simulations for Animation. Symposium on Computer Animation 2008. [video (mpeg4)]
• Multigrid Poisson solver
• A. McAdams, E. Sifakis, J. Teran, A Parallel Multigrid Poisson Solver for Fluids Simulation on Large Grids, ACM SIGGRAPH/Eurographics Symposium on Computer Animation (SCA) edited by M. Otaduy and Z. Popovic, pp.1-10, 2010. [PDF] [Video+Code]
• A coarse-grid Poisson solver
• Lentine, M., Zheng, W., and Fedkiw, R., A Novel Algorithm for Incompressible Flow Using Only A Coarse Grid Projection, SIGGRAPH 2010, ACM TOG 29, 4 (2010). [Video]

• Theodore Kim, Nils Thürey, Doug James, and Markus Gross. 2008. Wavelet turbulence for fluid simulation. ACM Trans. Graph. 27, 3, Article 50 (August 2008), 6 pages. [Project Webpage]
  
• Christopher Horvath and Willi Geiger. 2009. Directable, high-resolution simulation of fire on the GPU. In ACM SIGGRAPH 2009 papers (SIGGRAPH '09), Hugues Hoppe (Ed.). ACM, New York, NY, USA, , Article 41 , 8 pages.
  
• Jie Tan, Yuting Gu, Greg Turk, and C. Karen Liu. 2011. Articulated swimming creatures. ACM Trans. Graph. 30, 4, Article 58 (July 2011), 12 pages. [Project Page]
  

• Matthias Müller and Nuttapong Chentanez. 2011. Solid simulation with oriented particles. ACM Trans. Graph. 30, 4, Article 92 (July 2011), 10 pages. [YouTube Video]
  
• Shinjiro Sueda, Garrett L. Jones, David I. W. Levin, and Dinesh K. Pai. 2011. Large-scale dynamic simulation of highly constrained strands. In ACM SIGGRAPH 2011 papers (SIGGRAPH '11), Hugues Hoppe (Ed.). ACM, New York, NY, USA, , Article 39 , 10 pages. [Project Webpage]
  
• Breannan Smith, Danny M. Kaufman, Etienne Vouga, Rasmus Tamstorf, Eitan Grinspun, Reflections on simultaneous impact, ACM Transactions on Graphics (TOG), Volume 31 Issue 4, July 2012. [Project Webpage]
  

• Changxi Zheng and Doug L. James. 2009. Harmonic fluids. ACM Trans. Graph. 28, 3, Article 37 (July 2009), 12 pages. [Project Webpage]
  
• Changxi Zheng and Doug L. James. 2010. Rigid-body fracture sound with precomputed soundbanks. ACM Trans. Graph. 29, 4, Article 69 (July 2010), 13 pages. [Project Webpage]
  
• Jeffrey N. Chadwick, Changxi Zheng, and Doug L. James. 2012. Precomputed acceleration noise for improved rigid-body sound. ACM Trans. Graph. 31, 4, Article 103 (July 2012), 9 pages. [Project Webpage]
  

• Tim Langlois leads discussion of
  
• Real-time rendering of aerodynamic sound using sound textures based on computational fluid dynamics. Yoshinori Dobashi, Tsuyoshi Yamamoto, and Tomoyuki Nishita. 2003. ACM Trans. Graph. 22, 3 (July 2003), 732-740. DOI=10.1145/882262.882339 http://doi.acm.org/10.1145/882262.882339 
   (images) (movie) (pdf) (ppt)
• Submit comments before class to Piazza forum.

Project Demos

• Megan Comins leads discussion of
  
• Jeffrey Chadwick and Doug L. James, Animating Fire with Sound, ACM Transactions on Graphics, 30(4), August 2011.
• Submit comments before class to Piazza forum.

Topics discussed:

• Fluid equations (continuity, momentum, energy)
• Equations of linear acoustics; velocity potential; wave equations; sources
  
• Incompressible fluid case; pulsating sphere
  
• Free-space Green's function

Reference:

• M. S. Howe, Theory of Vortex Sound, Cambridge University Press, 2003. (Chapter 1 & 2)
  

• Phaedon Sinis & Arthur Sams lead discussion of
  
• Changxi Zheng and Doug L. James, Harmonic Fluids, ACM Transaction on Graphics, 28(3), July 2009, pp. 37:1-37:12. (or alternate fluid sound paper)
• Submit comments before class to Piazza forum.

Topics discussed [Nov07-Nov14]:

• Monopoles, dipoles, quadrupoles
• Acoustic energy and power
• Acoustic far field approximation
• Dipole and quadrupole source distributions
• Lighthill's acoustic analogy
• Curle's theory
• Helmholtz equation
• Frequency-domain sound sources; multipole expansions
  
• Acoustic energy & power
• Wave equation solvers

• Pedro Rittner leads discussion of
  
• Andrews, Steven S., and Dennis Bray. Stochastic simulation of chemical reactions with spatial resolution and single molecule detail. Physical biology, 1(3), 2004.
• Submit comments before class to Piazza forum.

• John DeCorato leads discussion of
  
• Stretchable and Twistable Bones for Skeletal Shape Deformation    
  Alec Jacobson, Olga Sorkine (ETH Zurich)
• Submit comments before class to Piazza forum.

• Caleb Woo leads discussion of
  
• [Shiratori et al. 2011] Motion Capture From Body-Mounted Cameras    
  
  
• Submit comments before class to Piazza forum.

References:

• J. E. Chadwick, D. R. Haumann, R. E. Parent, Layered construction for deformable animated characters, ACM SIGGRAPH Computer Graphics, v.23 n.3, p.243-252, July 1989. 
  
• N. Magnenat-Thalmann , R. Laperrière , D. Thalmann, Joint-dependent local deformations for hand animation and object grasping, Proceedings on Graphics interface '88, p.26-33, December 1989, Edmonton, Alberta, Canada.
• Ferdi Scheepers, Richard E. Parent, Wayne E. Carlson, Stephen F. May, Anatomy-based modeling of the human musculature, Proceedings of the 24th annual conference on Computer graphics and interactive techniques, p.163-172, August 1997.
• Tony DeRose, Michael Kass, Tien Truong, Subdivision surfaces in character animation, Proceedings of the 25th annual conference on Computer graphics and interactive techniques, p.85-94, July 1998.
• J. P. Lewis, Matt Cordner and Nickson Fong, Pose Space Deformations: A Unified Approach to Shape Interpolation and Skeleton-Driven Deformation, Proceedings of ACM SIGGRAPH 2000. pp. 165-172, 2000. 
  
• Peter-Pike J. Sloan, Charles F. Rose III and Michael F. Cohen, Shape by Example, 2001 ACM Symposium on Interactive 3D Graphics. pp. 135-144, 2001.
  
• Xiaohuan Corina Wang and Cary Phillips, Multi-Weight Enveloping: Least-Squares Approximation Techniques for Skin Animation, ACM SIGGRAPH Symposium on Computer Animation. pp. 129-138, 2002.
• Doug L. James, Dinesh K. Pai, DyRT: dynamic response textures for real time deformation simulation with graphics hardware, ACM Transactions on Graphics (TOG), v.21 n.3, July 2002.
• Paul G. Kry, Doug L. James and Dinesh K. Pai, EigenSkin: Real Time Large Deformation Character Skinning in Hardware, ACM SIGGRAPH Symposium on Computer Animation. pp. 153-160, 2002.
• Steve Capell, Seth Green, Brian Curless, Tom Duchamp, Zoran Popović, Interactive skeleton-driven dynamic deformations, ACM Transactions on Graphics (TOG), v.21 n.3, July 2002.
• Brett Allen, Brian Curless, Zoran Popović, The space of human body shapes: reconstruction and parameterization from range scans, ACM Transactions on Graphics (TOG), v.22 n.3, July 2003.
• Alex Mohr and Michael Gleicher, Building Efficient, Accurate Character Skins From Examples, ACM Transactions on Graphics. 22(3), pp. 562-568, 2003.
• Ladislav Kavan, Jiří Žára, Spherical blend skinning: a real-time deformation of articulated models, Proceedings of the 2005 symposium on Interactive 3D graphics and games, April 03-06, 2005, Washington, District of Columbia.
• Doug L. James, Christopher D. Twigg, Skinning mesh animations, ACM Transactions on Graphics (TOG), v.24 n.3, July 2005.
• Sang Il Park, Jessica K. Hodgins, Capturing and animating skin deformation in human motion, ACM Transactions on Graphics (TOG), v.25 n.3, July 2006
• Joseph Teran, Eftychios Sifakis, Geoffrey Irving, Ronald Fedkiw, Robust quasistatic finite elements and flesh simulation, Proceedings of the 2005 ACM SIGGRAPH/Eurographics symposium on Computer animation, July 29-31, 2005, Los Angeles, California.
• Robert Y. Wang, Kari Pulli, and Jovan Popović. 2007. Real-time enveloping with rotational regression. In ACM SIGGRAPH 2007 papers (SIGGRAPH '07). ACM, New York, NY, USA, Article 73. [YouTube Video]
• Ladislav Kavan, Steven Collins, Jiri Zara and Carol O'Sullivan, Skinning with Dual Quaternions, 2007 ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games, ACM Press, pages 39-46, April/May, 2007.
• ...
• Modern production example: Weta's "Tissue" software system; YouTube video for AMPAS award; 2
  

• John Oliver leads discussion of
  
• Synthesis of Detailed Hand Manipulations Using Contact Sampling
  Yuting Ye, Karen Liu (Georgia Institute of Technology)
  ACM Trans. Graph. (SIGGRAPH 2012) 31(4), Article 41.
• Submit comments before class to Piazza forum.

References:

• Mark Meyer and John Anderson, Key Point Subspace Acceleration and soft caching. In ACM SIGGRAPH 2007 papers (SIGGRAPH '07). ACM, New York, NY, USA, , Article 74, 2007. [webpage]
  
• Tao Ju, Scott Schaefer, and Joe Warren, Mean value coordinates for closed triangular meshes. In ACM SIGGRAPH 2005 Papers (SIGGRAPH '05), Markus Gross (Ed.). ACM, New York, NY, USA, 561-566, 2005.
• Pushkar Joshi, Mark Meyer, Tony DeRose, Brian Green, and Tom Sanocki. 2007. Harmonic coordinates for character articulation. ACM Trans. Graph. 26, 3, Article 71 (July 2007). [webpage]
• Yaron Lipman, David Levin, and Daniel Cohen-Or. Green Coordinates. ACM Trans. Graph. 27, 3, Article 78 (August 2008), 10 pages, 2008. 
• Ofir Weber, Roi Poranne and Craig Gotsman, Biharmonic Coordinates, Computer Graphics Forum Vol.31, No. 8, 2012.
  
  

• Bounding volumes (spheres, boxes, k-DOPs, etc)
• Separating axis theorem
• Space-time bounds
• Bounding moving points
• Bounding subspace deformations; 
  
• Bounded Deformation Trees
• O(r) and O(1) updates
• Spheres, boxes, k-DOPs
• Translational and affine/rotational models
• Self-collision culling
• Subspace and energy-based bounds
• Representative triangles
• Precomputed inter-object penetration depth approximations
  

• Philip M. Hubbard. 1996. Approximating polyhedra with spheres for time-critical collision detection. ACM Trans. Graph. 15, 3 (July 1996), 179-210. DOI=10.1145/231731.231732 http://doi.acm.org/10.1145/231731.231732
• B. Gaertner, Fast and Robust Smallest Enclosing Balls, Lecture Notes in Computer Science, Springer, pp. 325-338, 1999.
• Miniball software, Smallest Enclosing Balls of Points - Fast and Robust in C++.
• Doug L. James, Dinesh K. Pai, BD-Tree: Output-sensitive collision detection for reduced deformable models, ACM Transactions on Graphics, 23(3), August 2004, pp. 393-398. [SIGGRAPH Talk]
  
• M. Teschner et al., Collision Detection for Deformable Objects, Eurographics State-of-the-Art Report (EG-STAR), Eurographics Association, pages 119-139, 2004.
• Jernej Barbič and Doug L. James, Six-DoF haptic rendering of contact between geometrically complex reduced deformable models, IEEE Transactions on Haptics, 1(1):39–52, 2008. [Project page]
• Sean Curtis, Rasmus Tamstorf, and Dinesh Manocha. 2008. Fast collision detection for deformable models using representative-triangles. In Proceedings of the 2008 symposium on Interactive 3D graphics and games (I3D '08). ACM, New York, NY, USA, 61-69.
  
• Jernej Barbic and Doug L. James, Subspace Self-Collision Culling, ACM Transactions on Graphics (SIGGRAPH 2010), 29(3), July 2010, pp. 81:1-81:9.
  
• Changxi Zheng and Doug L. James, Energy-based Self-Collision Culling for Arbitrary Mesh Deformations, ACM Transaction on Graphics (SIGGRAPH 2012), 31(4), August, 2012.
• Jia Pan, Xinyu Zhang, and Dinesh Manocha. 2013. Efficient penetration depth approximation using active learning. Pattern Recogn. Lett. 34, 13, Article 191 (November 2013), 12 pages.

• Eston
• John & John
• Karl
• James
• Deniz

• Caleb
• Pedro
• Tim
• Dan
• Patrick