Computational Motion
Read for next class:
WedFeb2
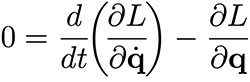
References for Lagrangian dynamics:
- V.I. Arnold, Mathematical
Methods
of
Classical
Mechanics, Springer, 2nd edition, 1989. (more
mathematical text)
- H. Goldstein et al., Classical
Mechanics, Addison Wesley, 3rd edition, 2001. (standard ugrad
physics text)
- S.T. Thornton and J.B. Marion, Classical Dynamics of Particles and Systems,
Brooks
Cole,
5th
edition,
2003.
(easier
ugrad
physics
text)
- N-body problems (all-pairs complexity)
- Reduced-coordinate deformable bodies (spatial/integration complexity)
- 2D serial manipulator (recursive complexity)
- Post discussion comments on group before class.
Assignment #1 for Wed Feb 9 (homework due in class):
Regarding the simplified N-body planar serial manipulator from class: Given joint angles and velocities, what is the complexity of naive evaluation of joint accelerations from the expanded Euler-Lagrange equations? Provide evidence to support your claim using the equations.
Cloth Motion
![From [Baraff and Witkin 1998]](images/thumb_BarWit98.jpg)
- Modeling cloth with energy terms
- Implicit integration
- Tensor calculus recap:
Discussed
differentiating the
following quantities with respect to particle position vectors, p_i:
- constant, c
- position, p_j
- vectors, (p_j-p_k)
- distances, ||p_j-p_k||
- distance powers, ||p_j-p_k||^n
- dot products, (p_1-p_0)^T (p_3-p_2)
- cross products
- ...
- Baraff, D. and Witkin, A. 1998. Large steps in cloth simulation. In Proceedings of the 25th Annual Conference on Computer Graphics and interactive Techniques SIGGRAPH '98. ACM, New York, NY, 43-54.
- Jonathan Richard Shewchuk, An Introduction to the Conjugate Gradient Method Without the Agonizing Pain, August 1994. PDF (516k, 58 pages)
- Discussion group posts
Assignment #2 for Mon Feb 21 class (homework due in class): Derive forces/Jacobians for [Baraff & Witkin 1998] (assignment (PDF)).
MonFeb14
![Diagram of SE(3) from [Kaufman et al. 2005]](images/thumb_SE%283%29.jpg)
- Rotational and rigid motion; kinematics and dynamics
- SO(3), Special Orthogonal group in 3D
- SE(3), Special Euclidean group in 3D
- Rigid-body motion
- Spatial velocity vectors (contravariant twists);
se(3); transformation
- Kinetic energy; inertia, principal axes
- Spatial forces (covariant wrenches); se*(3); transformation
- Velocity of contact points, and relation to twists
- Forces at contact points, and relation to wrenches
- Newton-Euler equations of motion
- Integrating rigid-body dynamics
- Deformable bodies; mode matrix, U; extensions
to framework
- David Baraff and Andrew Witkin, Physically Based Modeling, Online SIGGRAPH 2001 Course Notes, 2001.
- Murray, R. M., Sastry, S. S., and Zexiang, Li, A Mathematical Introduction to Robotic Manipulation. 1st. CRC Press, Inc., 1994.
- See summary in appendix of:
- Danny M. Kaufman, Timothy Edmunds and Dinesh K. Pai, Fast Frictional Dynamics for Rigid Bodies, ACM Transactions on Graphics (SIGGRAPH 2005), 24(3), August 2005.
- Ball's screw theory
- Ahmed A. Shabana, Dynamics of Multibody Systems, Cambridge, 3rd ed, 2005.
Parallel Rigid-Body Dynamics
- Takahiro Harada, Real-Time Rigid Body Simulation on GPUs, GPU Gems 3, 2007.
- A simple parallel method for RB dynamics with penalty
contact.
WedFeb16
- Algorithms overview
- Forward and inverse kinematics
- Inverse dynamics (control)
- Forward dynamics (simulation)
- Notation
- Recurrence relations
- Recursive Newton-Euler Algorithm (RNEA)
- O(N) inverse dynamics
- Composite-Rigid-Body Algorithm (CRBA)
- O(n^2) mass matrix
- Usage in O(N^3) forward dynamics (CRBA + RNEA + dense solve)
- Articulated-Body Algorithm (ABA)
- a.k.a. "Featherstone's algorithm"
- O(N) forward dynamics
- Closed-loop systems
- Constraints and fast solution methods
- Global analysis techniques
- Fast robot algorithms as sparse matrix methods
- Roy Featherstone and David Orin, Robot Dynamics: Equations and Algorithms,
Proc.
IEEE
Int.
Conf.
Robotics
&
Automation,
San
Francisco,
CA,
2000,
pp.
826–834.
(an
excellent
review)
- Roy Featherstone, Robot Dynamics Algorithms, Kluwer Academic Publishers, 1987. (classic book--highly readable)
- Roy Featherstone, A Divide-and-Conquer Articulated-Body
Algorithm for Parallel O(log(n)) Calculation of Rigid-Body Dynamics.
Part 1: Basic Algorithm, The International Journal of
Robotics Research, Vol. 18, No. 9, 867-875, 1999. (has good
appendix on spatial notation)
- Roy Featherstone, Rigid Body Dynamics Algorithms, Boston: Springer, 2007.
- E. Kokkevis, Practical Physics for Articulated Characters,
Proc.
of
Game
Developers
Conference
(GDC),
2004.
(good
overview
of
system
integration
issues
for
ABA,
e.g.,
handling
contact
and
constraints)
- David Baraff, Linear-Time Dynamics using Lagrange Multipliers, Proceedings of SIGGRAPH 96, Computer Graphics Proceedings, Annual Conference Series, August 1996, pp. 137-146.
- Robot
dynamics, Scholarpedia page.
- D.K. Pai, STRANDS: Interactive Simulation of Thin Solids using Cosserat Models, Computer Graphics Forum, 21(3), pp. 347-352, 2002.
Articulated Body Algorithm (ABA)
- E. Kokkevis, Practical Physics for Articulated Characters, Proc. of Game Developers Conference (GDC), 2004. (good overview of system integration issues for ABA, e.g., handling contact and constraints)
![From [Hairer and Wanner]](images/thumb_constraints.jpg)
- U.M. Ascher and L.R. Petzold, Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations, SIAM.
- E. Hairer and G. Wanner, Solving Ordinary Differential Equations II:
Stiff and Differential-Algebraic Problems, 2nd edition,
Springer, 1996.
- See Chapter VII.(1-2) Differential-Algebraic Equations of Higher Index
- Constrained Lagrangian dynamics
(CLD)
- Holonomic constraints
- Constraint-augmented Lagrangian
- Examples, e.g., pendulum
- DAE systems
- Differentiation index
- Structure of index-1, -2, and -3 DAE systems
- Index reduction by differentiation
- Drift-off phenomena
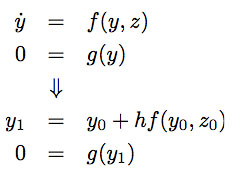
- Constrained Lagrangian dynamics in index-1, -2, -3 and GGL DAE forms
- Solving for Lagrange multiplier from index-1 form.
- Constraint stabilization:
- Baumgarte's method; modified Lagrange multiplier
- Projection (position, velocity)
- Implicit integration of DAEs (for stiff problems)
- General DAEs, and semi-explicit index-1 DAEs
- Backwards Euler
- BDF and multistep methods
- Half-explicit Runge-Kutta methods
- Methods for ODEs on manifolds
- Poststabilization
- Coordinate projection (c.f. coordinate resetting)
- Hamiltonian dynamics; energy conservation
- Symplectic integrators w/ constraints (SHAKE & RATTLE)
David Baraff and Andrew Witkin, Physically Based Modeling, Online SIGGRAPH 2001 Course Notes, 2001.
![[Iben et al. 2009]](http://graphics.eecs.berkeley.edu/site_root/papers/Iben-RPP-2009-04/thumb.jpg)
- Hayley N. Iben, James F. O'Brien, and Erik D. Demaine. "Refolding Planar Polygons". Discrete and Computational Geometry, 41(3):444–460, April 2009.
![House of cards from [Kaufman et al. 2008]](images/thumb_SP.jpg)
- Impact models; restitution coefficient
- Nonpenetration constraints
- Linear complementarity problems (LCP); QP formulations; Dantzig's algorithm
- Friction
- Painleve's paradox; frictional indeterminacy; frictional inconsistency; the importance of impulses
- Velocity-level contact formulation
- The myth of "contact points"; distributed friction forces; planar sliding; center of friction
- Contacting multibody systems
- Nonpenetration constraints; Signorini-Fichera condition
- Maximal dissipation principle
- "Staggered Projections" contact algorithm
- Iterative solvers; projected Gauss-Seidel methods
- D.E. Stewart, Rigid-Body Dynamics with Friction and Impact, SIAM Review, 42(1), pp. 3-39, 2000.
- D. Baraff, Fast contact force computation for nonpenetrating rigid bodies, Computer Graphics Proceedings, Annual Conference Series: 23-34, 1994. (cover's Dantzig's algorithm)
- D. Baraff, Coping with friction for non-penetrating rigid body simulation, Computer Graphics 25(4): 31-40, 1991. (cover's frictional indeterminacy & inconsistency)
- Danny M. Kaufman, Shinjiro Sueda, Doug L. James and Dinesh K. Pai, Staggered Projections for Frictional Contact in Multibody Systems, ACM Trans. Graph.(Proc. SIGGRAPH Asia), 27, 2008.
- Brian Mirtich, Impulse-based Dynamic Simulation of Rigid Body Systems, Ph.D. thesis, UC Berkeley, 1996.
- Eran Guendelman , Robert Bridson , Ronald Fedkiw, Nonconvex
rigid
bodies
with
stacking, ACM Transactions on Graphics (TOG),
v.22 n.3, July 2003 [doi>10.1145/882262.882358] (good example of a velocity-level
iterative contact solver)
- Kenny Erleben, Velocity-based shock
propagation for multibody dynamics animation, ACM Transactions on Graphics, 26(2), June 2007, pp. 12:1-12:20. (good summary of a velocity-level
projected Gauss-Seidel contact solver)
- Christopher D. Twigg, Doug L. James, Backward Steps in Rigid Body Simulation, ACM Transactions on Graphics, 27(3), August 2008, pp. 25:1-25:10.
(see for summary of
velocity-level contact problem)

![[Molino et al. 2004]](images/thumb_VNode.jpg)
--> Project planning day
- Hand in proposal in Wednesday Feb 9 class.
- Get feedback then get
cracking.
- Discussion of [Parker and O'Brien 2009]
- Submit project proposals
- Informal discussion of proposed course projects; revisions
- BOOM
Showcase at 4pm
- Eric G. Parker and James F. O'Brien. "Real-Time Deformation and Fracture in a Game Environment". In Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation, pages 156–166, August 2009.
Staggered Projections
MonMar28
WedMar30
![From [Enright et al. 2002]](http://graphics.stanford.edu/papers/water-sg02/sm_f0057.jpg)
- Advection; upwind differencing; ENO schemes
- Incompressibility constraint
- Navier-Stokes equation
- MAC grid discretization; interpolation and
averaging; upwinding
- Time-stepping schemes (Eulerian, and semi-Lagrangian)
- Projection to divergence-free velocity
- Poisson equation; discretization; compatibility
condition; PCG solution
- DAE view of incompressible flow
- Higher-order semi-Lagrangian schemes; monotone
interpolation; BFECC; CIP and USCIP
- S. Osher and R. Fedkiw, Level Set Methods and Dynamic Implicit
Surfaces, Applied Mathematical Sciences, volume 153,
Springer-Verlag, 2003.
- U.M. Ascher and L.R. Petzold, Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations, SIAM.
- Jos Stam,
Stable Fluids, Proceedings of
SIGGRAPH 99, Computer Graphics Proceedings, Annual Conference Series,
August 1999, pp. 121-128.
- Ronald Fedkiw, Jos Stam, Henrik Wann Jensen, Visual Simulation of Smoke, Proceedings of ACM SIGGRAPH 2001, Computer Graphics Proceedings, Annual Conference Series, August 2001, pp. 15-22. (introduces vorticity confinement forces)
- Bridson, R., Fedkiw, R., and Muller-Fischer, M. 2006. Fluid simulation: SIGGRAPH 2006 course notes, In ACM SIGGRAPH 2006 Courses (Boston, Massachusetts, July 30 - August 03, 2006). SIGGRAPH '06. ACM Press, New York, NY, 1-87. [Slides]
- Foster, N. and Fedkiw, R., Practical Animation of Liquids, SIGGRAPH 2001, 15-22 (2001).
- Enright, D., Marschner, S. and Fedkiw, R., Animation and Rendering of Complex Water Surfaces, SIGGRAPH 2002, ACM TOG 21, 736-744 (2002).
- Yongning Zhu , Robert Bridson, Animating sand as a fluid, ACM Transactions on Graphics (TOG), v.24 n.3, July 2005. (Discusses PIC and FLIP hybrid particle/grid methods)
- Higher-order advection schemes:
- BFECC and MacCormack methods:
- Byungmoon Kim, Yingjie Liu, Ignacio Llamas, Jarek
Rossignac,
Advections with Significantly Reduced Dissipation and Diffusion, IEEE Transactions on Visualization and Computer Graphics, Volume 13, Issue 1, Pages 135-144, 2007. video(DivX) - Selle, A., Fedkiw, R., Kim, B., Liu, Y., and Rossignac,
J. 2008. An Unconditionally Stable MacCormack Method.
J. Sci. Comput. 35, 2-3 (Jun. 2008), 350-371.
- Methods with small stencils (constrained interpolation profile (CIP)):
- Doyub Kim, Oh-young Song, Hyeong-Seok Ko, A Semi-Lagrangian CIP Fluid Solver without Dimensional Splitting, Computer Graphics Forum, 27(2), April 2008, pp. 467-475. (project page with videos)
- A projection method to approximate complex boundaries:
- Jeroen Molemaker, Jonathan M. Cohen, Sanjit Patel, Jun-yong Noh. Low Viscosity Flow Simulations for Animation. Symposium on Computer Animation 2008. [video (mpeg4)]
- Multigrid Poisson solver
- A. McAdams, E. Sifakis, J. Teran, A Parallel Multigrid Poisson Solver for Fluids Simulation on Large Grids, ACM SIGGRAPH/Eurographics Symposium on Computer Animation (SCA) edited by M. Otaduy and Z. Popovic, pp.1-10, 2010. [PDF] [Video+Code]
- A coarse-grid Poisson solver
- Lentine, M., Zheng, W., and Fedkiw, R., A Novel Algorithm for Incompressible Flow Using Only A Coarse Grid Projection, SIGGRAPH 2010, ACM TOG 29, 4 (2010). [Video]
WedMar23
- Each project group will give a short 5-minute presentation on their project topic, current results/progress, and goals for the remaining month.
Mon11Apr
![From [Sumner and Popovic 2004]](images/thumb_defoTransfer.jpg)
- Robert W. Sumner, Jovan Popović, Deformation transfer for triangle meshes, ACM Transactions on Graphics, 23(3), August 2004, pp. 399-405.
- Robert W. Sumner, Matthias Zwicker, Craig Gotsman, Jovan
Popović, Mesh-based Inverse Kinematics,
ACM Transactions on Graphics, 24(3), August 2005, pp. 488-495.

L. Kharevych, Weiwei, Y. Tong, E. Kanso, J. E. Marsden, P. Schröder, and Mathieu Desbrun
ACM/EG Symposium on Computer Animation 2006, pp. 43-51

- Mark Meyer, John Anderson, Key Point Subspace Acceleration and Soft Caching, ACM Transactions on Graphics, 26(3), July 2007, pp. 74:1-74:8.
- Pushkar Joshi, Mark Meyer, Tony DeRose, Brian Green, Tom Sanocki, Harmonic Coordinates for Character Articulation, ACM Transactions on Graphics, 26(3), July 2007, pp. 71:1-71:9.
Mon18Apr
Subspace Deformation Bounds
![3601 plastic chairs from [James and Pai 2004]](http://graphics.cs.cmu.edu/projects/bdtree/BDTreeChairs.gif)
- Bounding volumes (spheres, boxes, k-DOPs, etc)
- Separating axis theorem
- Space-time bounds
- Bounding moving points
- Bounding subspace deformations;
- Bounded Deformation Trees
- O(r) and O(1) updates
- Spheres, boxes, k-DOPs
- Translational and affine/rotational models
- Philip M. Hubbard. 1996. Approximating polyhedra with spheres for time-critical collision detection. ACM Trans. Graph. 15, 3 (July 1996), 179-210. DOI=10.1145/231731.231732 http://doi.acm.org/10.1145/231731.231732
- B. Gaertner, Fast and Robust Smallest Enclosing Balls, Lecture Notes in Computer Science, Springer, pp. 325-338, 1999.
- Miniball software, Smallest Enclosing Balls of Points - Fast and Robust in C++.
- Doug L. James, Dinesh K. Pai, BD-Tree: Output-sensitive collision
detection for reduced deformable models, ACM Transactions on
Graphics, 23(3), August 2004, pp. 393-398. [SIGGRAPH
Talk]
- M. Teschner et al., Collision Detection for Deformable Objects, Eurographics State-of-the-Art Report (EG-STAR), Eurographics Association, pages 119-139, 2004.
- Jernej Barbič and Doug L. James, Six-DoF haptic rendering of contact between
geometrically complex reduced deformable models, IEEE
Transactions on Haptics, 1(1):39–52, 2008. [Project page]

![[Ozgen et al. 2010] [Ozgen et al. 2010]](http://graphics.ucmerced.edu/%7Eoozgen/paper-tog-10/ex.png)
Physics-Based Sound Rendering
- Dimensional model reduction
- linear & nonlinear dynamics
- linear integration; IIR digital filter
- generalized eigenvalue problem; mass normalization
- Newmark integration
- full vs subspace
- explicit & implicit
- Reduced-order deformation force models
- exact reductions (linear, StVK)
- approximations (cubature)
- Reduced-order fluids
- Sound rendering
- rigid bodies
- nonlinear thin shells; mode coupling
- S. R. Idelsohn and A. Cardona, A Reduction Method for Nonlinear Structural
Dynamic Analysis, Computer Methods in Applied Mechanics and
Engineering 49, 253-279, 1985.
- A. A. Shabana, Theory of
Vibration (Volume II: Discrete and Continuous Systems),
Springer-Verlag, New York, NY, 1990.
- P. Krysl, S. Lall, and J.E. Marsden, Dimensional model reduction in non-linear finite element dynamics of solids and structures, Int. J. for Numerical Methods in Engineering, 51, 479-504, 2001.
- Doug L. James, Dinesh K. Pai, DyRT: Dynamic Response Textures for Real Time Deformation Simulation With Graphics Hardware, ACM Transactions on Graphics, 21(3), July 2002, pp. 582-585.
- Jernej Barbič and Doug L. James, Real-Time Subspace Integration of St.Venant-Kirchhoff Deformable Models, ACM Transactions on Graphics (ACM SIGGRAPH 2005), 24(3), pp. 982-990, August 2005, pp. 982-990.
- Adrien Treuille, Andrew Lewis, Zoran Popović, Model reduction for real-time fluids,
ACM
Transactions
on
Graphics, 25(3), July 2006, pp. 826-834.
- Steven An, Theodore Kim and Doug L. James, Optimizing Cubature for Efficient Integration of Subspace Deformations, ACM Transactions on Graphics (SIGGRAPH ASIA Conference Proceedings), 27(5), December 2008, pp. 165:1-165:10.
- Theodore Kim and Doug L. James, Skipping Steps in Deformable Simulation with Online Model Reduction, ACM Transactions on Graphics (SIGGRAPH ASIA Conference Proceedings), 28(5), December 2009, pp. 123:1-123:9.
- Jeffrey Chadwick, Steven An, and Doug L. James, Harmonic Shells: A Practical Nonlinear
Sound Model for Near-Rigid Thin Shells, ACM Transactions on
Graphics (SIGGRAPH ASIA Conference Proceedings), 28(5), December 2009,
pp. 119:1-119:10.

- Sound rendering problems
- Acoustic radiation problems
- Sound waves
- Derivation of wave equation
- Approximation
- Application to solids and fluids
- Case study: Harmonic Fluids
- K. van den Doel and D. K. Pai, The Sounds of Physical Shapes, Presence: Teleoperators and Virtual Environments, 7:4, The MIT Press, 1998. pp. 382--395.
- Kees van den Doel, Paul G. Kry, Dinesh K. Pai, FoleyAutomatic: Physically-Based Sound
Effects for Interactive Simulation and Animation,
Proceedings of
ACM SIGGRAPH 2001, Computer Graphics Proceedings, Annual Conference
Series, August 2001, pp. 537-544. [Video]
- Dinesh K. Pai, Kees van den Doel, Doug L. James, Jochen
Lang, John E. Lloyd, Joshua L. Richmond, Som H. Yau, Scanning Physical Interaction Behavior of
3D Objects, Proceedings of ACM SIGGRAPH 2001, Computer
Graphics
Proceedings, Annual Conference Series, August 2001, pp. 87-96. [Video]
- James F. O'Brien, Perry R. Cook, Georg Essl, Synthesizing Sounds From Physically Based Motion, Proceedings of ACM SIGGRAPH 2001, Computer Graphics Proceedings, Annual Conference Series, August 2001, pp. 529-536.
- Perry R. Cook, Sound Production and Modeling, IEEE Computer Graphics & Applications, 22(4), July-August 2002, pp. 23-27.
- Yoshinori Dobashi, Tsuyoshi Yamamoto, Tomoyuki Nishita, Real-Time Rendering of Aerodynamic Sound
Using Sound Textures Based on Computational Fluid Dynamics,
ACM Transactions on Graphics, 22(3), July 2003, pp. 732-740. [project
page]
- Doug L. James, Jernej Barbić and Dinesh K. Pai, Precomputed Acoustic Transfer:
Output-sensitive, accurate sound generation for geometrically complex
vibration sources, ACM Transactions on Graphics, 25(3), pp.
987-995, July 2006, pp. 987-995.
- Changxi Zheng and Doug L. James, Harmonic Fluids, ACM Transaction on Graphics (SIGGRAPH 2009), 28(3), August 2009, pp. 37:1-37:12.
- Jeffrey Chadwick, Steven An, and Doug L. James, Harmonic Shells: A Practical Nonlinear Sound Model for Near-Rigid Thin Shells, ACM Transactions on Graphics (SIGGRAPH ASIA Conference Proceedings), 28(5), December 2009, pp. 119:1-119:10.
- Changxi Zheng and Doug L. James, Rigid-Body Fracture Sound with Precomputed Soundbanks, ACM Transactions on Graphics (SIGGRAPH 2010), 29(3), July 2010, pp. 69:1-69:13.
- Changxi Zheng and Doug L. James, Toward High-Quality Modal Contact Sound, SIGGRAPH 2011 (to appear)
Huamin Wang, Gavin Miller and Greg Turk. 2007. "Solving General Shallow Wave Equations on Surfaces". In Proceedings of ACM SIGGRAPH/Eurographics Symposium on Computer Animation (SCA) 2007, pp. 229 -- 238, San Diego, USA. [PDF 2.3MB], [AVI in DivX 46MB] [BibTex]
Project Presentations (Part I)
- Kevin & Ivo
- Greg & Nathan
- Albert
- Chuck & Mark
- Himanshu & Jonathan
Project Presentations (Part II)
- Jeff
- Andy
- Ian
- Yunfeng
- Jiexun
Due Date
![[Parker et al. 2009] [Parker et al. 2009]](http://graphics.cs.berkeley.edu/papers/Parker-RTD-2009-08/video_thumb.png)
![[Lentine et al. 2010] [Lentine et al. 2010]](http://physbam.stanford.edu/%7Emlentine/images/refinement-small.png)

![Pouring water with thousands of acoustic bubbles [Zheng and James 2009]](http://www.cs.cornell.edu/%7Edjames/research/pics/thumb_harmonicFluids.jpg)
