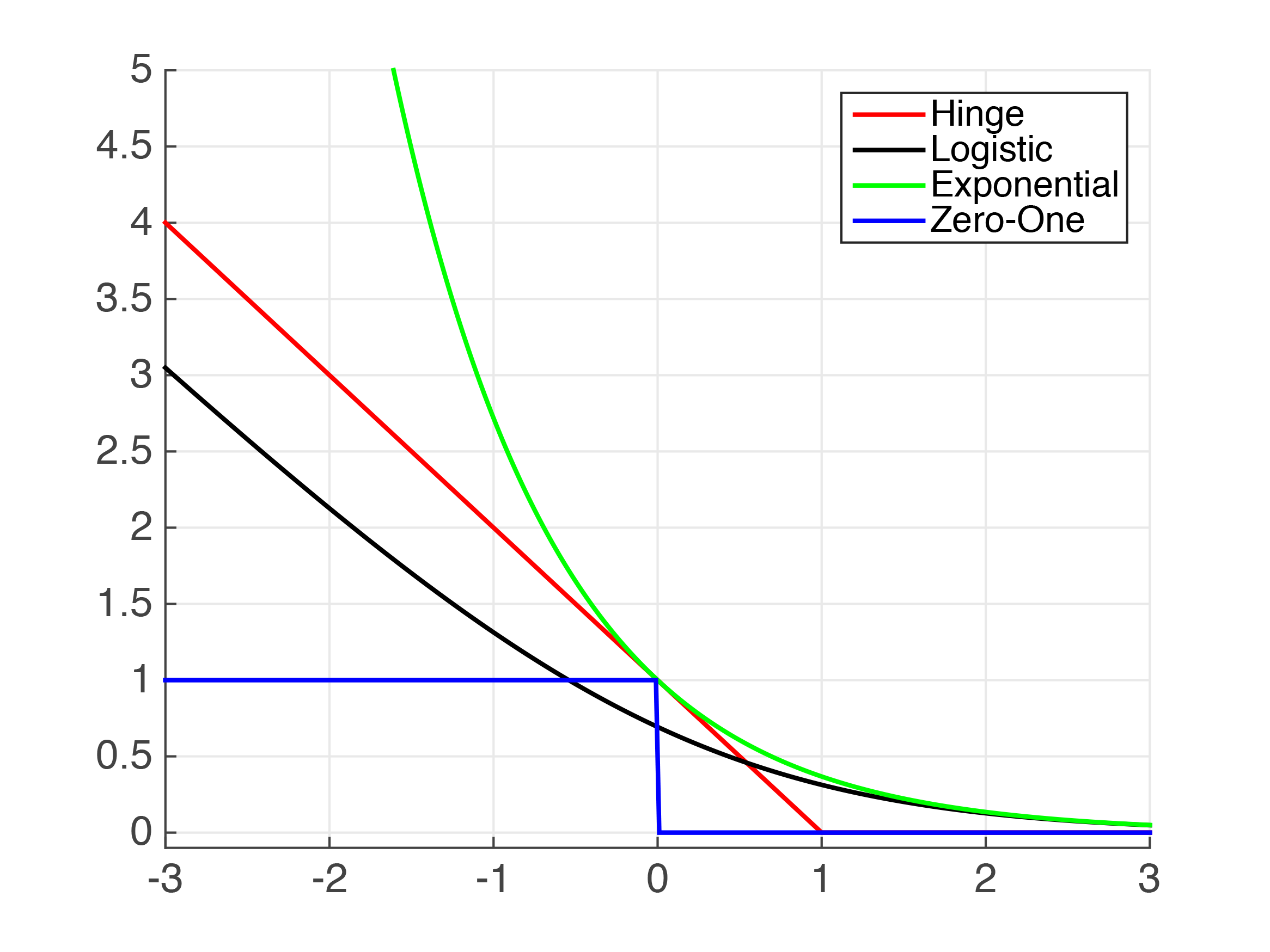
Figure 4.1: Plots of Common Classification Loss Functions - x-axis: $\left.h(\mathbf{x}_{i})y_{i}\right.$, or "correctness" of prediction; y-axis: loss value
| Loss $\ell(h_{\mathbf{w}}(\mathbf{x}_i,y_i))$ | Usage | Comments | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hinge-Loss$\max\left[1-h_{\mathbf{w}}(\mathbf{x}_{i})y_{i},0\right]^{p}$ | When used for Standard SVM, the loss function denotes the size of the margin between linear separator and its closest points in either class. Only differentiable everywhere with $\left.p=2\right.$. | ||||||||||||||||
| Log-Loss $\left.\log(1+e^{-h_{\mathbf{w}}(\mathbf{x}_{i})y_{i}})\right.$ | Logistic Regression | One of the most popular loss functions in Machine Learning, since its outputs are well-calibrated probabilities. | |||||||||||||||
| Exponential Loss $\left. e^{-h_{\mathbf{w}}(\mathbf{x}_{i})y_{i}}\right.$ | AdaBoost | This function is very aggressive. The loss of a mis-prediction increases exponentially with the value of $-h_{\mathbf{w}}(\mathbf{x}_i)y_i$. This can lead to nice convergence results, for example in the case of Adaboost, but it can also cause problems with noisy data. | |||||||||||||||
| Zero-One Loss $\left.\delta(\textrm{sign}(h_{\mathbf{w}}(\mathbf{x}_{i}))\neq y_{i})\right.$ | Actual Classification Loss | Non-continuous and thus impractical to optimize. |
Some questions about the loss functions:
Figure 4.1: Plots of Common Classification Loss Functions - x-axis: $\left.h(\mathbf{x}_{i})y_{i}\right.$, or "correctness" of prediction; y-axis: loss value
| Loss $\ell(h_{\mathbf{w}}(\mathbf{x}_i,y_i))$ | Comments | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Squared Loss $\left.(h(\mathbf{x}_{i})-y_{i})^{2}\right.$ |
|
||||||||||
| Absolute Loss $\left.|h(\mathbf{x}_{i})-y_{i}|\right.$ |
|
||||||||||
Huber Loss
|
|
||||||||||
| Log-Cosh Loss $\left.log(cosh(h(\mathbf{x}_{i})-y_{i}))\right.$, $\left.cosh(x)=\frac{e^{x}+e^{-x}}{2}\right.$ | ADVANTAGE: Similar to Huber Loss, but twice differentiable everywhere |
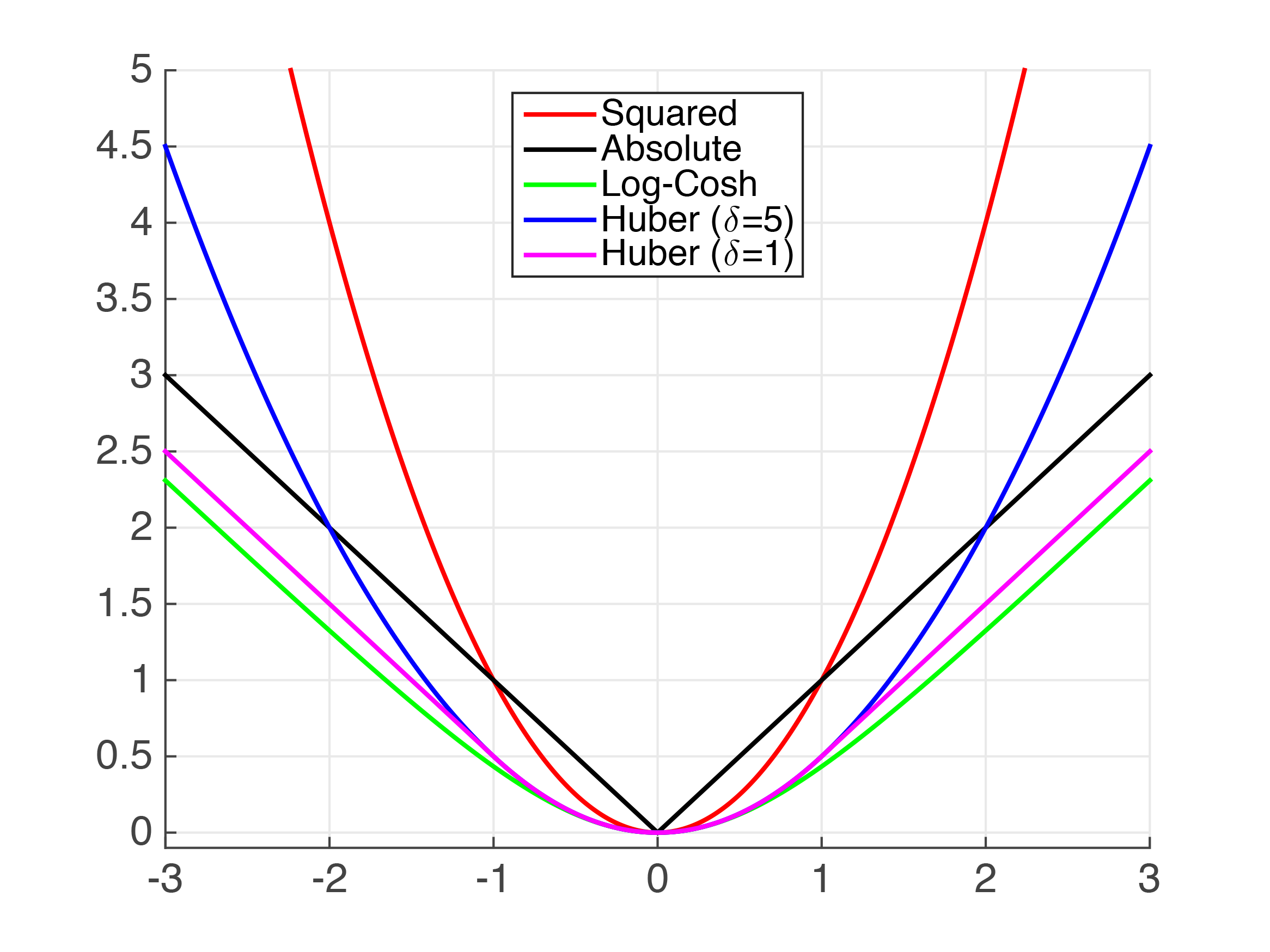
Figure 4.2: Plots of Common Regression Loss Functions - x-axis: $\left.h(\mathbf{x}_{i})y_{i}\right.$, or "error" of prediction; y-axis: loss value
| Regularizer $r(\mathbf{w})$ | Properties | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| $l_{2}$-Regularization $\left.r(\mathbf{w}) = \mathbf{w}^{\top}\mathbf{w} = \|{\mathbf{w}}\|_{2}^{2}\right.$ |
|
||||||||||
| $l_{1}$-Regularization $\left.r(\mathbf{w}) = \|\mathbf{w}\|_{1}\right.$ |
|
||||||||||
| Elastic Net $\left.\alpha\|\mathbf{w}\|_{1}+(1-\alpha)\|{\mathbf{w}}\|_{2}^{2}\right.$ $\left.\alpha\in[0, 1)\right.$ |
|
||||||||||
| $l_p$-Norm $\left.\|{\mathbf{w}}\|_{p} = (\sum\limits_{i=1}^d v_{i}^{p})^{1/p}\right.$ |
|

Figure 4.3: Plots of Common Regularizers
| Loss and Regularizer | Comments | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ordinary Least Squares $\min_{\mathbf{w}} \frac{1}{n}\sum\limits_{i=1}^n (\mathbf{w}^{\top}x_{i}-y_{i})^{2}$ |
|
||||||||||
| Ridge Regression $\min_{\mathbf{w}} \frac{1}{n}\sum\limits_{i=1}^n (\mathbf{w}^{\top}x_{i}-y_{i})^{2}+\lambda\|{w}\|_{2}^{2}$ |
|
||||||||||
| Lasso $\min_{\mathbf{w}} \frac{1}{n}\sum\limits_{i=1}^n (\mathbf{w}^{\top}\mathbf{x}_{i}-{y}_{i})^{2}+\lambda\|\mathbf{w}\|_{1}$ |
|
||||||||||
| Logistic Regression $\min_{\mathbf{w},b} \frac{1}{n}\sum\limits_{i=1}^n \log{(1+e^{-y_i(\mathbf{w}^{\top}\mathbf{x}_{i}+b)})}$ |
|
||||||||||
| Linear Support Vector Machine $\min_{\mathbf{w},b} C\sum\limits_{i=1}^n \max[1-y_{i}\mathbf{w}^\top{\mathbf{x}_i})]+\|\mathbf{w}\|_2^2$ |
|
||||||||||