Chapter 13 One-sided Matchings: House Allocation Problems

In this chapter, mirroring our treatment of voting, we revisit the matching market problem in a setting without money transfers; we refer to these type of problems as one-sided matchings as only nodes on one “side” of the bipartite graph (namely, individuals on the “left”) have preferences over the nodes on the other side (namely, the items on the “right”). These type of problems are often also called house allocation problems. (Later on in chapter 14, we turn to considering also a “two-sided” version of the problem where nodes on both sides have preferences over one another.)

13.1 (One-sided) Matching Contexts

Recall that a matching market frame $(n, Y, v)$ specifies a set $[n]$ of players, a set $Y$ of objects (e.g., “houses”) such that $| Y | = n$ , and a player valuation function $v : Y \to ℕ$ . Recall that from such a matching market frame, we defined a notion of a matching market context $(n, Ω, T, v)$ :

$Ω$ (the set of states) is the set of possible matchings $M$ in the complete bipartite graph over $[n] \cup Y$ ;
for each player $i$ , $T_{i}$ is the set of possible valuation functions $v : Y \to ℕ$ ;
$v_{i} (t, M) = t (M (i))$ .

As we saw in chapter 10, for every matching market context, we can use the VCG mechanism to DST-implement social value maximization.

In this section, following the voting paradigm discussed in chapter 11, we consider a different type of mechanism design context where players’ types simply specify preference ordering over the possible objects. Additionally, given that items now do not have prices, we restrict the state space $Ω$ to the set of perfect matchings in the complete bipartite graph over $[n] \cup Y$ (i.e., matchings where all players get allocated an item).

More formally, consider a mechanism design context $(n, Ω, T, v)$ where:

$Ω$ is the set of all possible perfect matchings $M$ in the complete bipartite graph over $[n] \cup Y$ , where $Y$ is some finite set such that $| Y | = n$ ;
for each player $i$ , the type space $T_{i}$ is a set of preferences over the objects $Y$ (i.e., each $μ \in T_{i}$ is a ranking $μ = (y_{1}, \dots, y_{n})$ of the elements in $Y$ ).
for every player $i$ , $μ \in T_{i}$ , $v_{i} (μ, M) \geq v_{i} (μ, M^{'})$ if $M (i) >_{μ} M^{'} (i)$ (i.e., player $i$ is happier if they get allocated an object they prefer).

We refer to such a context as a (one-sided) matching context (as opposed to a “matching market context”); if it always holds that $v_{i} (t, x) > v_{i} (t, x^{'})$ (i.e., we have strict inequality) when $x$ is higher ranked than $x^{'}$ according to $t$ , we refer to the context as a matching context with strict preferences. Furthermore, if for each player $i$ , $T_{i}$ is the full set of preferences over $Y$ (i.e., all orderings over $Y$ are possible), we refer to the context as a complete matching context.

As with voting, we restrict our attention to payment-free mechanisms: We refer to a payment-free mechanism $𝒱$ for a matching context as a matching rule $𝒱$ , and refer to DST matching rules as strategy-proof matching rules.

13.2 Strategy-proof Matching Rules: Serial Dictatorship

At first one may think that the Gibbard–Satterthwaite theorem directly applies also to strategy-proof matching rules. Indeed, there is a sense in which it does: if players had strict preferences over all of $Ω$ (i.e., the set of all possible allocations $M$ ), then by the Gibbard–Satterthwaite theorem, we would directly have that every strategy-proof matching mechanism (over at least 3 possible allocations) must be dictatorial. But, in a matching context, players cannot have strict preferences over the full set of allocations; rather, a player $i$ can only have strict preferences over objects the player get allocated—their utility is independent of what objects are allocated to players $- i$ . Thus, a matching context can be viewed as a restricted (as opposed to a complete) social-choice context, and we may thus hope to overcome the Gibbard–Satterthwaite impossibility result.

Indeed, as we now show, a nontrivial (and actually quite useful) mechanism is possible! Given a matching context $Γ = (n, Ω, T, v)$ , and given some permutation $π$ of the players $[n]$ (i.e., an ordering of the players), consider the following “serial dictatorship mechanism” $𝒱$ . Start with player $π (1)$ (the “first dictator”) and let that player be allocated their top choice; next, move on to player $π (2)$ (the “second dictator”), and let that player pick their top unallocated choice, and so on. (See Figure 13.1 for an illustration.)

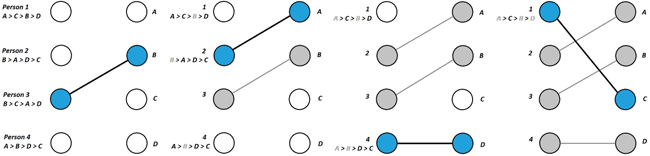
**Figure 13.1:** An example of the process of serial dictatorship in a matching between four players and four items. The ordering of dictators in this case is $(3, 2, 4, 1)$ ; each player’s preferences are shown in the illustration, and at each step the current dictator selects their most preferred remaining choice (highlighted in blue).

We refer to this mechanism as the Serial Dictator Mechanism (SDM) with respect to the ordering $π$ and denote it by $S D M_{π}$ ; this mechanism is sometimes also referred to as the priority mechanism.

Theorem 13.1. For any matching context $Γ = (n, Ω, T, v)$ and any ordering $π$ of the players $[n]$ , we have that the SDM with respect to $π$ is strategy-proof for $Γ$ .

Proof. Consider the “first dictator” $π (1)$ ; clearly this player gets their first choice, so can never gain anything by not truthfully reporting their preferences.

Now consider instead some later dictator $π (i)$ that gets to pick in the $i$ th iteration of the mechanism. By reporting their preferences truthfully this player gets their top choice of the currently unallocated items. By deviating, it can never get an item that has already been allocated (since the mechanism never reallocates items); thus, by deviating, the player can only get allocated an item that is less (or as) desirable.

■

When preferences are strict, this simple mechanism also produces an allocation that is “optimal” in the sense no subset of the players can improve their utility without hurting some other player:

Definition 13.1. Given a matching context $Γ = (n, Ω, T, v)$ , we say that an allocation $M \in Ω$ is Pareto-optimal with respect to $\vec{μ} \in T$ if there does not exist some $M^{'} \in Ω$ such that:

For all $i \in [n]$ , $v_{i} (μ_{i}, M^{'} (i)) \geq v_{i} (μ_{i}, M (i))$ (i.e., every player is at least as well off);
There exists some $i \in [n]$ such that $v_{i} (μ_{i}, M^{'} (i)) > v_{i} (μ_{i}, M (i))$ (i.e., some player is strictly better off).

Theorem 13.2. For any matching context $Γ = (n, Ω, T, v)$ with strict preferences, any ordering $π$ of the players $[n]$ , any $\vec{μ} \in T$ , we have that $S D M_{π} (\vec{t})$ is Pareto-optimal with respect to $\vec{μ}$ .

Proof. Consider some type profile $\vec{μ}$ , and let $a = S D M_{π} (\vec{μ})$ . Consider any matching $M^{'}$ where all players $i$ get allocated an item $M^{'} (i)$ that they like as much as $M (i)$ (i.e., no player is worse off). As we now show, then it must hold that $M^{'} = M$ , which concludes the proof.

First, note that clearly $M^{'} (π (1)) = M (π (1))$ since the first dictator gets their top choice (which is unique by the strict preference assumption). It inductively follows that $M^{'} (π (i)) = M (π (i))$ for every $i \in [n]$ since dictator $i$ gets it first choice of the currently unallocated items (which again is unique). Thus, $M^{'} = M$ .

■

Note that in the above proof, we crucially rely on the fact that preferences are strict; without this restrictions the SDM may output an allocation that is not Pareto-optimal (show it!).

The SDM mechanism is commonly used in practice: for instance, for office allocations for professors, for the New York City school choice system, university housing allocations, and so on. For all these examples, we typically select the dictatorship order $π$ at random.

13.3 Uniqueness of Serial Dictatorship [Advanced]

Despite all of the above-mentioned the nice features of the SDM, there is something unappealing about it—once the order is fixed, the mechanism is very unfair. A natural question is whether this unfairness is needed. As we shall not see, there is a sense in which it is: We present a variant of the Gibbard–Satterthwaite theorem that shows that the only strategy-proof mechanism satisfying two natural properties—neutrality and non-bossiness—is the SDM:

We say that a matching rule $𝒱$ is neutral if the allocation it produces is independent of the names of the objects; that is, the outcome would be the same if the objects were renamed. More precisely, for any permutation $σ$ over the outcomes $X$ , and any preference profile $\vec{μ}$ , we have: $𝒱 (σ (\vec{μ})) = σ (𝒱 (\vec{μ})),$
where $σ (\vec{μ})$ denotes the preference profile obtained by applying the permutation $σ$ to every component of $\vec{μ}$ .

We say that a matching rule

𝒱

is non-bossy if a player cannot change the allocation of others without changing their own allocation. More precisely, for every preference profile

\vec{μ}

, every player

i

, and every preference ordering

μ_{i}^{'}

for player

i

, if

𝒱 (\vec{μ}) \neq 𝒱 (μ_{i}^{'}, {\vec{μ}}_{- i})

, then

𝒱 (\vec{μ}) (i) \neq 𝒱 (μ_{i}^{'}, {\vec{μ}}_{- i}) (i)

Clearly, SDM satisfies both of these properties.

We are now ready to state the uniqueness theorem. As for voting contexts, we restrict our attention to complete matching contexts with strict preferences.

Theorem 13.3. Let $𝒱$ be a neutral and non-bossy matching rule for a complete matching context with strict preferences $(n, Ω, T, v)$ . Then there exists some permutation $π$ over $[n]$ such that $𝒱 = S D M_{π}$ .

13.4 Proof of the Uniqueness Theorem [Advanced]

In this section, we prove Theorem 13.3. The proof follows a similar (but actually simpler) structure as the proof of the Gibbard-Satterthwaite theorem. Again, for simplicity of notation, in the remainder of this section, we always have some fixed complete matching context $Γ$ with strict preferences in mind (and as such, whenever we write, for instance, strategy-proof, neutral, or non-bossy, we mean with respect to this matching market context).

We start by defining the analog of monotonicity for matching mechanisms.

Definition 13.2. A matching rule $𝒱$ is monotone if for every two preference profiles $\vec{μ}$ and ${\vec{μ}}^{'}$ , if $𝒱 (\vec{μ}) = M$ , and for every player $i$ and every choice $y$ such that $M (i) >_{μ_{i}} y$ it is also true that $M (i) >_{μ_{i}^{'}} y$ , it follows that $𝒱 ({\vec{μ}}^{'}) = M$ .

In other words, if a matching rule is monotone, then a winning allocation $M$ will continue to win as long as for every player $i$ , all candidates that are dominated by $i$ ’s allocation, $M (i)$ , continue to be dominated by $M (i)$ .

Essentially the same proof that shows that strategy-proof voting rules are monotone shows that strategy-proof and non-bossy matching rules are monotone—the only minor difference is that we need non-bossiness to deal with the fact that player preferences are not strict over the full set of allocations (but rather only strict over each players’ own choices). For convenience, we repeat the proof and highlight (in italics) where non-bossiness is used.

Lemma 13.1. If a strategy-proof matching rule $𝒱$ is non-bossy, then it is also monotone.

Proof. Assume for the sake of contradiction that $𝒱$ is not monotone; then, there exist profiles of preferences $\vec{μ}$ and ${\vec{μ}}^{'}$ so that $𝒱 (\vec{μ}) = M$ and for every player $i$ and every choice $y$ such that $M (i) >_{μ_{i}} y$ it is also true that $M (i) >_{μ_{i}^{'}} y$ , yet $𝒱 ({\vec{μ}}^{'}) \neq M$ .

As in the proof of Lemma 12.1, we construct a sequence of “hybrid” preferences ${\vec{μ}}^{k}$ where we move from $\vec{μ}$ to ${\vec{μ}}^{'}$ one player at a time:

$μ_{i}^{k} = μ_{i}$ if $i > k$ , and
$μ_{i}^{k} = μ_{i}^{'}$ if $i \leq k$ .

Thus, ${\vec{μ}}^{0} = \vec{μ}$ and ${\vec{μ}}^{n} = {\vec{μ}}^{'}$ . Now, let $k^{*}$ denote the smallest index where $𝒱 ({\vec{μ}}^{k^{*}}) = M$ but $𝒱 ({\vec{μ}}^{k^{*} + 1}) \neq M$ . Clearly such an index must exist, since $𝒱 ({\vec{μ}}^{n}) \neq M$ by assumption.

Furthermore, note that the only difference between ${\vec{μ}}^{k^{*}}$ and ${\vec{μ}}^{k^{*} + 1}$ is that player $k^{*} + 1$ is switching from $μ_{k^{*} + 1}$ to $μ_{k^{*} + 1}^{'}$ . By non-bossiness, we thus must have that $M^{'} (k^{*} + 1) \neq M (k^{*} + 1)$ ; that is, the allocation of player $k^{*} + 1$ changes to some $z \neq M (k^{*} + 1)$ when he switches strategies.

Since $𝒱$ is strategy-proof, we must have that $M (k^{*} + 1) >_{μ_{k^{*} + 1}} z$ , or else, given the preference profile ${\vec{μ}}^{k *}$ , player $k^{*} + 1$ would prefer to report $μ_{k^{*} + 1}^{'}$ , which would lead to the outcome $z$ that they strictly prefer to $M (k^{*} + 1)$ (by our assumption that preferences are strict). Since by the choice of $\vec{μ^{'}}$ , we have that for every player $i$ and every choice $y$ , if $M (i) >_{μ_{i}} y$ then $M (i) >_{μ_{i}^{'}} y$ , it follows that $M (k^{*} + 1) >_{μ_{k^{*} + 1}^{'}} z$ .

But, by the same argument, we have that $z >_{μ_{k^{*} + 1}^{'}} M (k^{*} + 1)$ (or else player $k^{*} + 1$ would prefer to report $μ_{k^{*} + 1}$ given the preference profile ${\vec{μ}}^{k * + 1}$ ); this is a contradiction (since preferences are strict).

■

We are now ready to prove Theorem 13.3.

Proof of Theorem 13.3. Consider some neutral and non-bossy matching rule $𝒱$ for $n$ players over some set of objects $X = {x_{1}, x_{2}, \dots x_{n}}$ . We show the existence of a permutation $π$ over $[n]$ such that $𝒱$ actually implements SDM with respect to $π$ .

To construct $π$ , consider the “lexicographic” preference profile $\vec{ν}$ where for every player $i$ , $ν_{i} = (x_{1}, x_{2}, x_{3}, \dots, x_{n})$ ; that is, they all prefer $x_{1} > x_{2} > x_{3} > \dots > x_{n}$ . Define $π$ as follows: let $π (i) = j$ if $𝒱 (\vec{ν}) (j) = x_{i}$ ; that is, let the player $j$ who receives object $i$ (i.e., $x_{i}$ ) in the matching output by $𝒱 (\vec{ν})$ be the “ $i^{th}$ dictator.” Since every player receives a different object in the matching, this uniquely defines $π$ .

We now show that $𝒱$ actually implements $S D M_{π}$ . Consider any preference profile $\vec{μ}$ . We aim to show that $𝒱 (\vec{μ}) = S D M_{π} (\vec{μ})$ . Let ${\vec{ν}}^{'}$ be the preference profile where for every player $i$ , $ν_{i}^{'} = (y_{1}, y_{2}, \dots, y_{n})$ where

y_{i} = S D M_{π} (\vec{μ}) (π (i)) .

That is, $y_{i}$ is the object received by the $i^{th}$ dictator if running $S D M_{π} (\vec{μ})$ .

By neutrality (renaming $x_{i}$ to $y_{i}$ ), it directly follows that for every $i$ ,

𝒱 ({\vec{ν}}^{'}) (π (i)) = y_{i} = S D M_{π} (\vec{μ}) (π (i))

and thus,

𝒱 ({\vec{ν}}^{'}) = S D M_{π} (\vec{μ}) .

As we now shall argue, by monotonicity (which follows from Lemma 13.1), it also holds that

𝒱 ({\vec{ν}}^{'}) = 𝒱 (\vec{μ}),

which will conclude the proof.

Consider the allocation $M = 𝒱 ({\vec{ν}}^{'})$ and for any $i$ , the $i^{th}$ dictator, player $π (i)$ . As argued above, this player is currently receiving object $M (π (i)) = y_{i}$ . To use monotonicity (to conclude that $𝒱 ({\vec{ν}}^{'}) = 𝒱 (\vec{μ})$ ) we need to argue that every object $y$ that is dominated by $y_{i}$ with respect to $\vec{ν}$ (i.e., objects $y_{j}$ such that $j > i)$ remain dominated by $y_{i}$ with respect to $\vec{μ}$ .

Assume for contradiction that this is not the case; that is, there exists some $y_{j}$ where $j > i$ that player $π (i)$ prefers to $y_{i}$ with respect to $\vec{μ}$ . Then, the $i^{th}$ dictator (i.e., player $π (i)$ ) in the execution $S D M_{π} (\vec{μ})$ would be assigned $y_{j}$ (since when it was their turn to choose, $y_{j}$ is still unassigned), which contradicts the definition of $y_{i}$ .

■

Notes

Shapley and Scarf were the first to study one-sided matching problems without payment [SS74]; the model we considered here—which typically is called the housing allocation model—is due to Hylland and Zeckhauser [HZ79]. The serial dictatorship mechanism and the notion of “non-bossiness” were introduced and studied by Satterthwaite and Sonnenschein [SS81]. The impossibility of non-serial dictatorship mechanisms is due to Svensson [Sve99]; our proof, however, is a simplified version of his proof (due to the fact that we have restricted our attention to bipartite graphs where $| X | = | Y |$ ).