Summarizing Diverging String Sequences, with Applications to Chain-Letter Petitions

Abstract

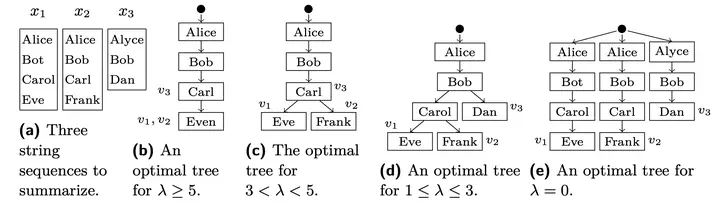
Algorithms to find optimal alignments among strings, or to find a parsimonious summary of a collection of strings, are well studied in a variety of contexts, addressing a wide range of interesting applications. In this paper, we consider chain letters, which contain a growing sequence of signatories added as the letter propagates. The unusual constellation of features exhibited by chain letters (one-ended growth, divergence, and mutation) make their propagation, and thus the corresponding reconstruction problem, both distinctive and rich. Here, inspired by these chain letters, we formally define the problem of computing an optimal summary of a set of diverging string sequences. From a collection of these sequences of names, with each sequence noisily corresponding to a branch of the unknown tree $T$ representing the letter’s true dissemination, can we efficiently and accurately reconstruct a tree $T’ \approx T$? In this paper, we give efficient exact algorithms for this summarization problem when the number of sequences is small; for larger sets of sequences, we prove hardness and provide an efficient heuristic algorithm. We evaluate this heuristic on synthetic data sets chosen to emulate real chain letters, showing that our algorithm is competitive with or better than previous approaches, and that it also comes close to finding the true trees in these synthetic datasets.