|
Octant provides a framework for aggressively extracting geographical
constraints from various sources of information, for efficiently representing
and operating on these constraints as a set of Bezier curves, and for providing
an error resilient way to combine constraints with questionable verity.
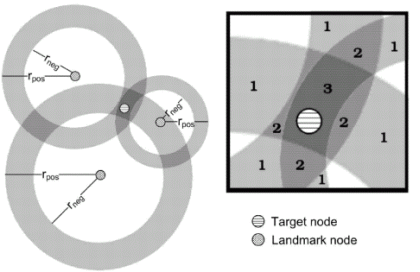
Latency measurements from known landmarks
Octant uses latency measurements from landmarks with known geographic
coordinates to the target as its primary source of geographical constraints.
The latency to distance mapping from a landmark to a target is calibrated
by the inter-landmark latency measurements. The goal of the calibration is
to compute two bounds from a given RTT to the target; the outer bound that
determines the maximum distance the target may be from the landmark
(positive information), and the inner bound that determines the minimum
distance the target may be from the landmark (negative information).
Intermediate routers as additional landmarks
|
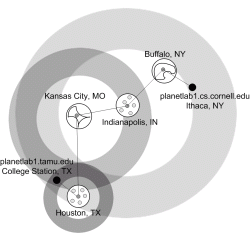
Intermediate routers between the landmarks and the target are also used
as additional landmarks. Octant uses the
undns
database to determine the rough geographic location of many of the
intermediate routers. For routers that are not found in the database,
Octant can still use their estimated location as inexact landmarks that
may not have a large effect on the precision of the result, but is effective
at providing additional redundancy for handling measurement uncertainties.
|
|
Using geographic and demographic information
Geographic and demographic constraints are also used in Octant to further
reduce the region size where the target may be located. For example, only
landmasses and areas with non-zero population are considered as possible
target locations.
Handling uncertainty
The above constraints, defined as regions bounded by a set of Bezier curves,
are each given weights based on Octant's estimate of their accuracies. When two
constraint regions overlap, the weights are added together. Weights enable
Octant to integrate constraints of questionable verity into the system.
Conflicting information can be introduced into the system at little risk of
overconstraining the final system and reducing its effectiveness.
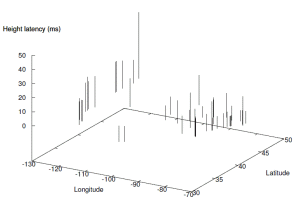
Queuing delays
To handle the effects of queuing delays on the accuracy of the
latency to distance mappings, a height metric is computed for each node
which represents its relative queuing delays and can be used to adjust
the size and value of the constraint regions that it contributes.
A node that consistently has a round-trip time (RTT) to other nodes that is
significantly higher than the minimum RTT will be assigned a higher height
than a node that has RTT values closer to the minimum. The minimum RTT
between two nodes is defined as the time light takes to travel twice the
great circle distance of the two nodes.
|
Vertical bars represent landmarks, their position corresponds to their
physical location, while the length of the bars corresponds to their
assigned heights.
|
Point selection
The final estimated region for a target is the union of the constraints with
the highest weights. Some applications can use such area estimates directly.
Yet many legacy applications are designed to accept target locations as single
points. In order to support legacy applications, Octant uses a Monte-Carlo
algorithm to pick a single point that represents the best estimate of the
target's location. The system initially selects thousands of random points
that lie within the estimated region. Each point is assigned a weight based
on the sum of its distances to the other selected points. After some number
of trials, the point with the least weight is chosen as the best estimate
of the target's location. Note that this point is guaranteed to be within the
estimated location area by definition, even if the area consists of disjoint
regions.
|