Upgrading Shortest Paths in Networks
We introduce a new general network improvement problem relevant. Many applications in areas as diverse as VLSI circuit design, QoS routing, and traffic engineering involve designing networks under constrained shortest paths and budget limits. For example, in a transportation network, a key goal is to connect major cities via short routes to better serve the bulk of the traffic. In a multicast communication setting where a single node is broadcasting to a set of subscribers, it is important to minimize the latency, or the shortest path delays between the source node and all the subscribers. In wildlife conservation, our motivating application from computational sustainability, the landscape connectivity between important habitat patches is measured as the length of the shortest path in terms of landscape resistance to animal movement. Maintaining good landscape connectivity, i.e. short resistance paths, is key to resilient wildlife populations in an increasingly fragmented habitat matrix.
In this work, we introduce a new general network improvement problem relevant in such settings. The problem is defined with respect to a network with node delays where the delay between a pair of nodes is the shortest path delay in the network, while the overall delay of the network is measured as the average delay among a designated set of node pairs. Given a set of node upgrade actions with respective costs and upgraded node delays, we seek to choose the best possible upgrade strategy in terms of minimizing total upgrade cost and resulting overall network delay. We refer to this problem as the Upgrading Shortest Paths Problem. We consider two optimization settings. In the budget-constrained setting, the goal is to find an upgrade strategy such that the total upgrade cost does not exceed a given budget B, and the resulting upgraded network has minimum overall delay over all possible strategies which obey the budget constraint. On the other hand, in the delay-constrained setting, the goal is to find a minimumcost set of nodes to be upgraded so that the overall delay in the resulting network meets a given bound D.
Conservation Planning for Landscape Connectivity
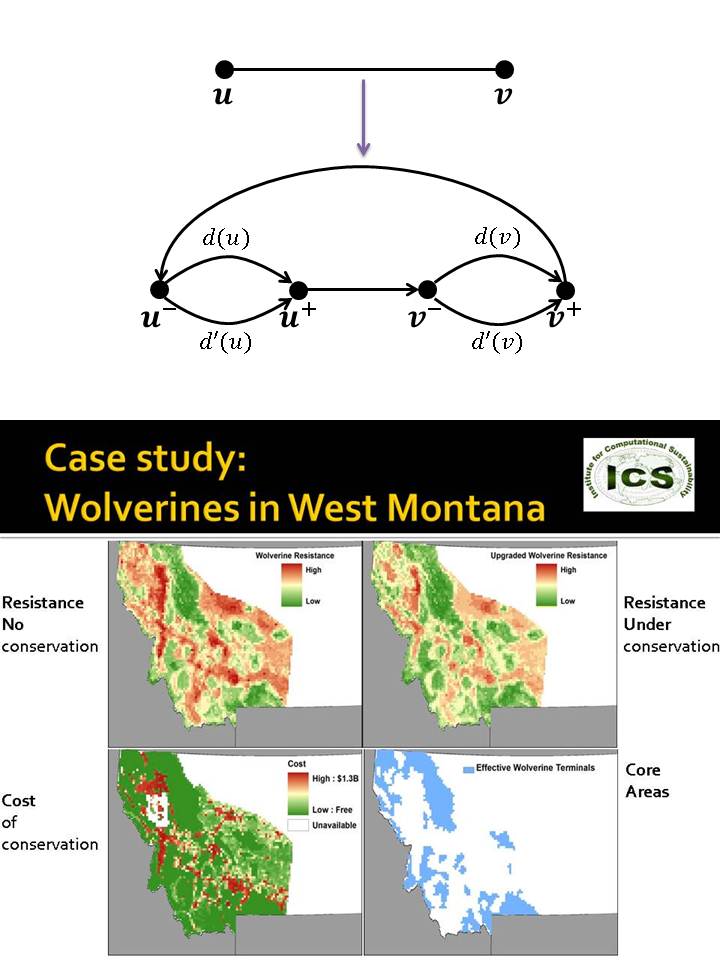
Habitat fragmentation is one of the principal threats to biodiversity. The focus of much ecology research is to quantify landscape connectivity, a measure of the degree to which the landscape facilitates or impedes movement among habitat patches. The landscape is represented as a set of small parcels or pixels, each of which has a resistance value that gives the species-specific cost of moving through particular landscape features. Under the Least-Cost Path model, the connectivity between two designated habitat patches is measured as the length of the shortest resistance-weighted path between them. Decision-support tools to design efficient budget-constrained conservation strategies are needed and yet still largely lacking.
In Wildlife Corridor Design, one conserves a set of parcels that form a network of protected land between designated reserves. In reality, choosing not to buy a piece of land may not significantly impact whether wildlife will still be able to use the land. In the landscape connectivity conservation problem, each land parcel may contribute to the connectivity of the terminals, whether or not it has been bought. The benefit of buying a piece of land is reflected by decreasing the landís effective resistance.
By reducing the problem of improving landscape connectivity to the Upgrading Shortest Paths problem, we provide conservation planners with a tool to evaluate trade offs between costs and connectivity benefits as well as generate conservation plans with formal optimality guarantees.
In an ongoing collaboration with USGS Rocky Mountain Research Station and Oregon State University, we are applying this methodology to consevration planning in Montana involving wolverines.
Publications
Upgrading Shortest Paths in Networks
Bistra Dilkina, Katherine Lai, Carla Gomes.
CPAIOR-11: International Conference on Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems, Berlin, Germany, May 2011.
[ PDF | BiBTeX ]
Extended talk presented at INFORMS Annual Meeting 2011 as:
Cost-effective Conservation Planning for Improved Landscape Connectivity (awarded Best Talk in the INFORMS 2011 Forestry Sessions)