Cornell University Department of Computer Science

Connected Subgraph Problem with Node Costs and Node Profits

A large class of decision and optimization problems can be captured as finding a connected subgraph of a larger graph satisfying certain cost and revenue requirements. In different realizations of the Connection Subgraph Problem costs and profits are associated with either edges, nodes or both. Examples of this family of problems are the Minimum Steiner Tree, Maximum-Weighted Connected Subgraph and Point-to-Point Connection Problem. Such problems arise in a large number of applications – e.g. network design, system biology, social networks and facility location planning.

Here, we are concerned with a variant of the Connected Subgraph Problem where we are given a graph with costs and profits associated with nodes and one or more designated nodes called terminals and we seek to find a connected subgraph that includes the terminals with maximal profit and total cost within a specified budget which we refer to as the Budget-Constrained Steiner Connected Subgraph Problem with Node Profits and Node Costs.

We adapted the directed Dantzig-Fulkerson-Johnson (DFJ) formulation with subtour elimination constraints, proposed for problems with edge costs. This formulation involves an exponential number of connectivity constraints that cannot be represented explicitly for real life sized instances. To address this, we developed a Bender’s decomposition approach that iteratively adds connectivity constraints to a relaxed master problem.

We show that, for critically constrained budgets, the DFJ encoding proposed here can find optimal or close to optimal solutions, dramatically speeding up runtime. For the same problem instances and budget levels, the previous state-of-the-art single flow encoding could only find considerably worse feasible solutions and much worse objective upper bounds.

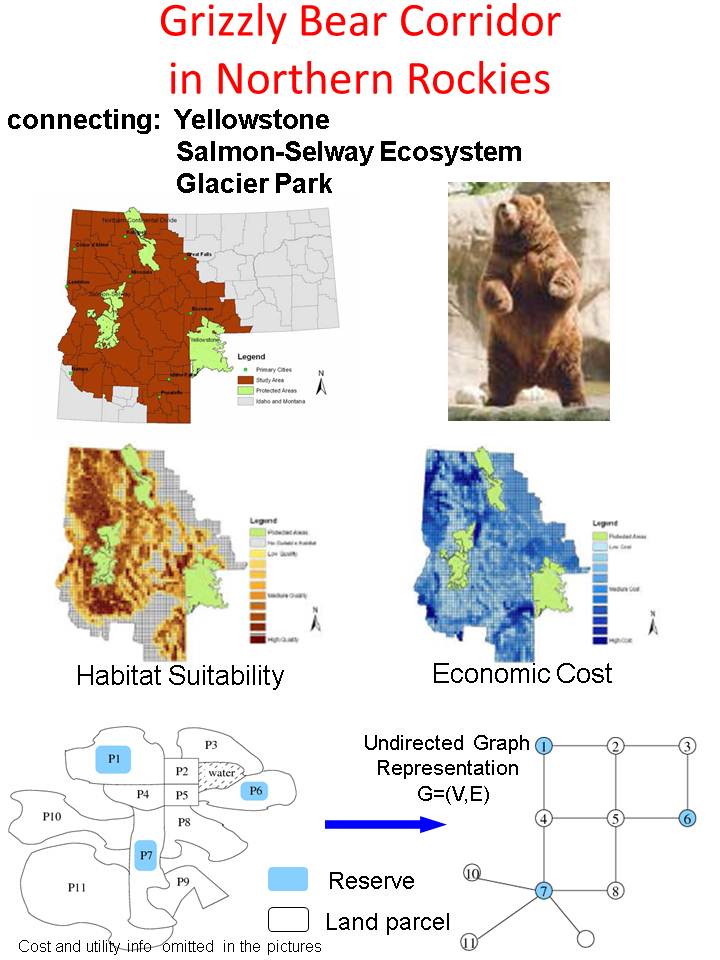
Wildlife Corridor Design

Our work is motivated by an important instance of this problem that arises in Conservation Planning. Biologists have highlighted the importance of addressing the negative ecological impacts of habitat fragmentation when selecting parcels for conservation. We look at the problem of designing so-called wildlife corridors to connect areas of biological significance (e.g. established reserves). Wildlife corridors are an important conservation method in that they increase the genetic diversity and allow for greater mobility (and hence better response to predation and stochastic events such as fire, as well as long term climate change). Specifically, in the wildlife corridor design problem, we are given a set of land parcels, a set of reserves (land parcels that correspond to biologically significant areas), and the cost (e.g. land value) and utility (e.g. habitat suitability) of each parcel. The goal is to select a subset of the parcels that forms a connected network including all reserves. This problem is clearly an instance of the Connected Subgraph Problem with node profits and node costs, where the nodes correspond to parcels, the terminal nodes correspond to the reserves and the edges correspond to adjacency of parcels. Conservation and land use planners generally operate with a limited budget while striving to secure the land that results in the corridor with best habitat suitability. This results in the budget-constrained version of the connected subgraph problem.