Bistra Dilkina, Postdoctoral Associate [Home]

Maximizing Cascades in Networks

Many natural processes — such as the diffusion of information in a social network or the spread of animals through a fragmented landscape—can be described as a network diffusion process or cascade. Diffusion processes are modeled by a network, where edges are associated with transmission probabilities. One would often like to intervene to steer the course of a cascade toward some goal, e.g., to maximize its spread through the network. However, typical interventions (e.g., choosing where to initiate a cascade) do not directly affect the cascade outcome; the cascade is a complex stochastic process that depends only probabilistically on the choices made. Previous work on cascades has only considered the question of selecting the set of k nodes to initiate a new cascade that will maximize its eventual spread.

We introduce a much more general optimization framework for cascades. In our model, one may choose from a rich set of management actions to manipulate a cascade: in addition to choosing where to initiate the cascade, these actions may also intervene directly in the network to change cascade dynamics by adding nodes. The model is general enough to also capture adding edges, or increasing the local probability of propagating the cascade.

We develop an approach based on Sample Average Approximation and Mixed Integer Programming, which provides solutions with stochastic optimality guarantees. Our results show that the optimal solutions generated by the SAA approach can be qualitatively different than the ones obtained by a myopic greedy approach.

Conservation Planning with Stochastic (meta)population models

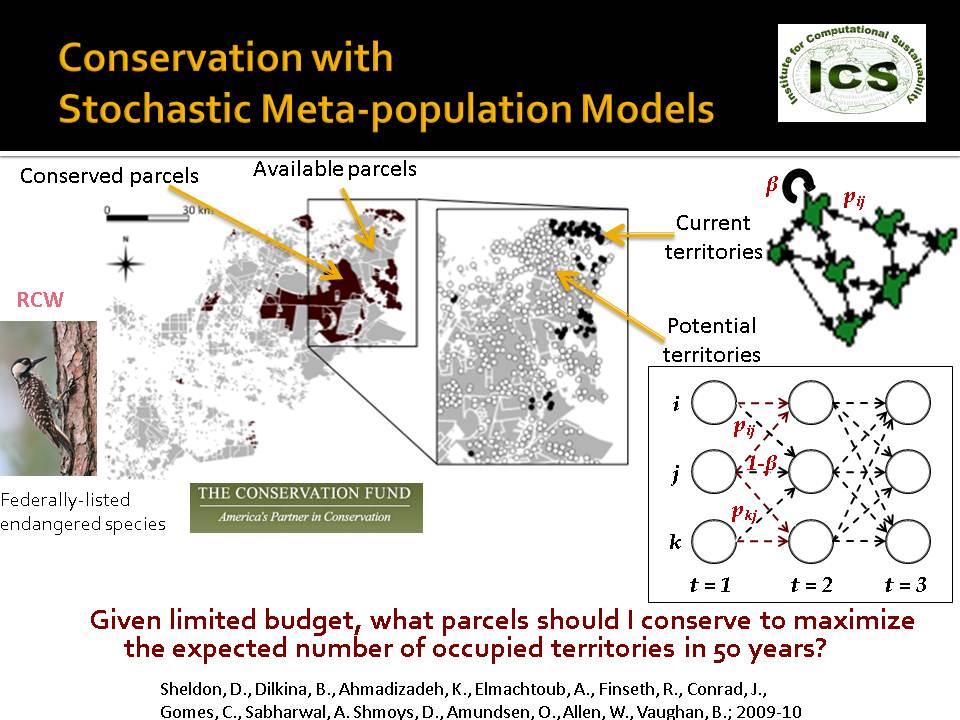
Meta-population models or spatially-explicit population models are often used to describe the population dynamics of species. For two patches i and j, the activation or colonization probability p(i,j) represents the probability that an individual from patch i will colonize unoccupied patch j in one time step. The extinction probability q(i) is the probability that the local population in patch i goes extinct in one time step. A metapopulation model is equivalent to a non-progressive cascade model that describes the occupancy of different habitat patches over some time horizon T, where node v(i,t) represents habitat patch i at time t.

Patches are grouped into non-overlapping parcels; some are already conserved, and the others are available for purchase at time 0 at a given cost. Assuming that the target species may only occupy conserved patchs and given a limited budget, the goal is to select a set of parcels to conserve such that the expected number of occupied patches at a given time horizon is maximized.

In a collaboration with The Conservation Fund, we applied this methodology to land conservation to assist the recovery of the Red-cockaded Woodpecker (RCW), a federally listed rare and endangered species. RCW are a “keystone species” in the southeastern US: they excavate tree cavities used by at least 27 other vertebrate species. However, habitat degradation has led to severe population declines, and existing populations are highly fragmented. As a result, habitat conservation and management are crucial to the continued viability of RCW.