CS631 Final Project
 
3D Morphing
 
Suwat Chitphakdibodin
 
Glen C Chang
 
Thibet Rungrotkitiyot
 
 
 
   
  6. Face Tracing
 
The edges can be adjusted in real-time when adding new vertexes and the related edges are splited if necessary.  However, the face information is lost after the process.  Although a topology can be described only by the network of vertexes and edges, the face information comes to handy when implementing the algorithm on popular graphic libraries, such as OpenGL.  This project uses OpenGL as the main resource for constructing the visual interface, so a special algorithm is created to reconstruct the entire face lists from the set of vertexes and edges provided after the PM1 and PM2 are merged on the common model with the Weiler’s algorithm.
 
Face Tracing : 3 Steps

1. Find the vertex list of all the polygon faces
2. Adjust Vertex list order of the face to be counter-clockwise
3. Reduce all polygons to triangles
 

1.  Face Tracing Algorithm
 
 
       
    For Each Egde 
      Use an iterative deepening search to find the minimum number of edge required to form a polygon face. 
      Repeat if desired (until each edge is marked exactly twice)
         
 

Figure 8 : Psuedocode for Face Tracing Algorithm
This is an abbreviated version of the actual algorithm.  Some special cases need to be considered, such as a polygon forming inside another polygon with same number of edges.  Breadth-first search can be used instead of iterative deepening search.  It’s faster at the cost of memory space required.
 
2.  Face adjustment

For rendering purposes, we would like to have the normals of all faces facing outward.  We use the right-hand rule (counter-clockwise) to determine the direction of the normal.  Using the vertices of one of the mapped model, we can calculate the normal of a polygon face and the vector from the center of the model to the face.  Calculate the dot product of the two, we can determine if the polygon is facing outward or inward.  If the polygon is facing inward, we simply reverse the order of the vertex list of the polygon face.
 
3.  Triangles-only club

We need to make sure all polygon faces are triangles since a triangle is always flat.  This is done for rendering purpose also.  We used a very simple method of reducing polygon to triangles.  Take any vertex of a face and draw a line to the rest of the vertices.  We can use this method since we are guaranteed to have convex polygon faces.
 
 

 
   7. Polygon Interpolation
 
Once all correspondence is established.  Both objects will have the same number of vertices and faces.  Faces in PM1 are mapped to faces in PM2.  The next step is just to interpolate from one to the other.  We explore 3 schemes of interpolation.
 
1.  Linear Symmetric Interpolation

This is the simplest scheme.  The coordinates X, Y and Z are linearly interpolated from PM1 to PM2 with the same rate.  The result is similar to putting the air to one object and it inflates to become the other.

2.  Non-Linear Symmetric Interpolation

The variant of this scheme is that the coordinates X, Y and Z are non-linearly (exponentially) interpolated from PM1 to PM2, but still with the same rate.  The result is similar to putting the air to one object and it inflates to become the other.  The different is that the object morph slowly at the beginning and fast at the end. 
 
3.  Non-Linear Non-Symmetric Interpolation

The variant of this scheme is that the coordinates X, Y and Z are not interpolated with the same rate.  The result is non-symmetric transformation.
 
 

 
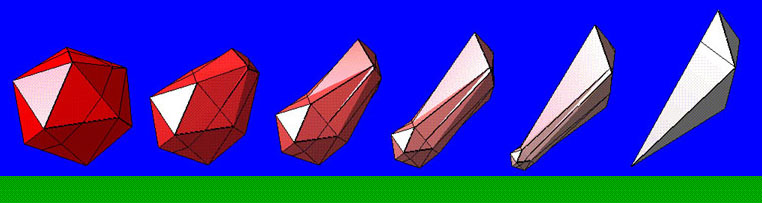Figure 9 : Linear Symmetric Interpolation
 
 
 
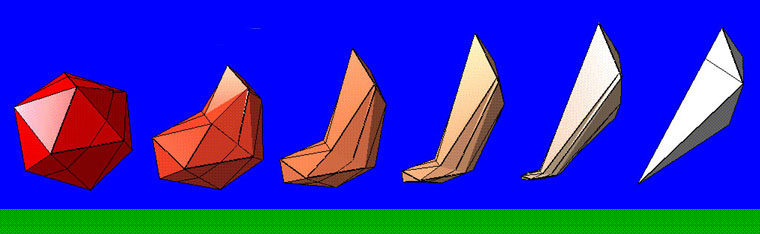Figure 10 : Non-Linear Symmetric Interpolation
 
 
 
 
   8. Applications
 
All examples can be downloaded.  The following keys are needed to activate the morphing.  Press "O" to indicate the object.  Press "F" to forward the morphing sequence.  Press "R" to reverse the morphing sequence.
 
 
 
Figure 11 : Complex Object Morphing
(Download Animation Program)
 
 
 
 
Figure 12 : Morph Across Window
(Download Animation Program)
 
 
 
 
Figure 13 : Object Integration and Disintegration
(Download Animation Program)
 
 
 
   9. Source Code Distribution
 
White Paper version can be downloaded from 3DMorph.doc file.  All sources are stored in 3DMorph.zip file.  They are tested on WinNT4.0 and Win95 platform.  OPenGL1.0 which usually come with WinNT and Win95 is needed for graphic library.  Although Microsoft Developer Studio VC++ version5 is used, any C compilers such as GNU or BORLAND should be able to use and developer platform.
 
 
 
   10. Summary
 
Future research need to be done to develop projections for general concave polyhedra with holes.   The new algorithm which can work under discontinuity  of object surface need to be explored.  The idea would be that the desired projection of the objects and subsequence polygon mapping could be carried out for the objects with the same number of holes.
 
This project is a part of Multimedia class - CS631 at Cornell University.  Any comments on the paper will be very much appreciated.  For more information, please contact the author.
 
 
 
   References
Back to Previous Page
 
 Created and  maintained by Suwat Chitphakdibodin.
This page was last modified on Friday May 1, 1998.
Contact the author suwatch@cs.cornell.edu
 
 Back to Top