Finding Redundant Structures in Data Flow Graphs

by Oliver Richardson, Alexa VanHattum, Gregory Yauney December 18, 2019

The source code for this project and our profiling analysis can be found here.

In a conventional von Neumann architecture, we might think of computation at a high level as our computers faithfully carrying out a series of steps. Like dominoes in a line, the program counter runs through each instruction once its predecessor completes.

Of course, this mental model is far from the truth—in modern out-of-order processors, instructions are aggressively reordered to take advantage of multiple processing elements at once. The major caveat here is that reordering must respect the original program's data flow. That is, if an instruction needs to use data that is generated by a previous instruction, then it cannot be reordered to happen beforehand. From this perspective, we can think of computation as dictating the flow of data through operations. Each instruction is a node, and dependencies form edges that flows along. These dependencies form a data flow graph (DFG) for the program.

Go with the flow 🌊

Analyzing the data flow graphs of programs allows us to think about the shape of the computation, independent of the literal order a programmer used to specify it. In particular, two separate programs are more likely to share data flow structure than literal source code redundancy (since many reorderings can maintain the same data flow). Even within the same source program, shared structure in the data flow graph may indicate core computational patterns.

Data flow graphs for computational acceleration

If our goal is to compile faster or more energy-efficient code, data flow graphs can help show us where to focus. By identifying redundant subgraphs in the structure of data flow graphs, we can find groupings of operations that we expect to occur frequently enough to benefit from additional optimization effort. What's more, the shape of the subgraphs is also a signal for how useful the acceleration might be: subgraphs that are wider, rather than simply linear chains, indicate more opportunity for fine-grained parallelism. Our goals in this project are shaped by the domain of hardware acceleration with heterogeneous computing, where a compiler's goal is to target multiple processors, each with differing strengths and weaknesses.

For this project, we build on the LLVM compiler infrastructure to find redundant structures in programs' static data flow graphs. Our goal is to find a fixed number of subgraph structures that occur the most frequently (that is, cover the highest number of instructions) throughout the program. We focus on finding candidate subgraphs with high frequency, and leave analysis and heterogeneous compilation of those subgraphs to later work.

Building data flow graphs from LLVM

Data flow graphs exist at multiple levels of abstraction in a compiler toolchain, and there are trade-offs to targeting any particular choice.

First, data flow graphs can either represent a program statically, purely from the program's source code, or dynamically, from a program execution trace. A static DFG has a one-to-one relation to the source code: each operation and its dependencies are directly translated. The control flow of the program exists only implicitly: if a data value's flow depends on the branching structure of the program, the DFG would have back edges and cycles. A dynamic DFG captures a single trace throughout the program, where operations are repeated each time they are executed. In this case, the data flow graph remains acyclic (with values only flowing "down"), and loops in the control flow repeat in the subgraph for each time the loop is executed. However, dynamic data flow graphs only represent a single execution of the program and may not even cover the full program behavior. They also may be infeasible to generate ahead of time for long-running applications, and they tend in practice to be so large as to limit analysis to fragments of the full dynamic DFGs.

In addition, DFGs can target either the intermediate representation level, with LLVM-level operations, or at the machine code level, with operations corresponding to the exact instruction set architecture. The machine code data flow graph corresponds more directly to the program's actual execution, but is not as general across different targets.

For this project, we use LLVM to target the static DFG at the intermediate representation level of abstraction. LLVM translates the program source to static single assignment (SSA) form, where every variable name can only be assigned to once. Because LLVM's in-memory intermediate representation stores pointers to instructions' operands, we can build a program's static data flow graph by inserting edges to an instruction and from each of its operands. We narrow the project's scope to only consider acyclic subgraphs by considering subgraphs only within basic block boundaries, which lack branching control flow.

Matching fixed DFG stencils

To begin, let's imagine we already have some oracle that has given us a great candidate subgraph (which we'll call a stencil), and our job is to find all the redundant instantiations of that stencil. If we consider a large program DFG G and a smaller stencil DFG H, the task is to find as many subgraph isomorphisms of H and G. Here, the larger program DFG G is generated directly from the LLVM in-memory representation as described above, but does not include edges across control flow boundaries. Rather, G is a collection of DFG components per basic block. In addition, we focus on operations that consume and produce values directly (such as arithmetic and shift operations) rather than those that read or write from memory or modify control flow (load, store, branch, and return).

While graph isomorphism is a notoriously tricky problem, it is also a common one, and we make heavy use of out-of-the-box graph algorithms. We employ the networkx.isomorphism Python package, which provides tools for iterating over matches (subgraph isomorphisms) between the program DFG G and a stencil DFG H. There are two features of a matching which distinguish it from a subgraph isomorphism: (1) nodes must be matched to nodes of the same opcode, which technically makes the problem a colored subgraph isomorphism (which fortunately makes the problem easier), and (2) we need to select mutually exclusive subgraphs, where each node can be assigned to at most once isomorphic instance (to model actual hardware acceleration). In the case of a single stencil, we use a greedy heuristic to randomly choose isomorphisms until there are no longer any remaining choices that are mutually exclusive. When trying to match multiple stencils, our heuristic tries to find the largest stencils first. We describe this search process in more detail in our implementation section.

We started our testing by hand-picking chains of instructions found in our benchmarking code. From the Embench embedded programming benchmarking suite, we used matmult-int.c to chose a few common chains of operations:

mul → add → srem

shl → add

sdiv → mul → add

As we expected, these small human-selected stencils subgraphs performed especially poorly. On the original program, matmult-int.c, these stencils only matched less than 4% of instructions.

Identifying common DFG stencils

Of course, finding the common subgraphs by hand is pretty antithetical to a reasonable approach at compiling code. Our real goal is to automate the process of finding the common DFG stencils to accelerate.

Formal description of the task

In this context of ignoring control flow and considering data flows within basic blocks, we can look at the problem purely graph-theoretically. For a single trace through the program, the data flow graph $G$ is acyclic, and we would like to cover as much of it as possible with subgraphs corresponding to the stencils that we accelerate. Statically, we do not know what the final data flow graph is, but we do know that we will be able to assemble one by connecting dangling edges from control-flow-free components: basic blocks.

We would like to find a small collection of graph components $\mathcal H = {H_i, \ldots, H_k}$, which we can use to replace parts of and accelerate programs having basic blocks $\mathcal G = {G_1,\ldots,G_n}$, that maximizes the total saved time:

$$\mathcal S_{\mathcal H}(\mathcal G) := \max_{\mathcal C \in \text{Cov}(\mathcal G, \mathcal H)}~ \sum_{G \in \mathcal G} w_G \cdot \sum_{H \in \mathcal C_G} f_H \cdot |H|$$

where:

• $\text{Cov}(\mathcal G, \mathcal H)$ is the set of all valid (partial) coverings of basic blocks with at most one stencil, that is, injective graph morphisms $\varphi: (\cup \mathcal G) \to \cup \mathcal H$.
• $\mathcal C_G$ is the component of the covering $\mathcal C$ of the total covering on the particular basic block graph $G$.
• $w_G$ is independent of $\mathcal H$ and proportional to the expected number of times $G$ is executed.
• $f_H$ is the expected speedup factor from accelerating the component $H$.

Now supposing that $f_H$ was roughly constant, we could achieve the maximum savings by trivially choosing $\mathcal H := \mathcal G$. There are a few problems with this:

1. $|\mathcal H|$ is large; there are many of these sub-graphs, which makes the search process substantially less efficient.
2. Each $H_i \in \mathcal H$ is also large, making the specialized component more expensive.
3. There is now a dependency between $\mathcal H$ and $\mathcal G$, and so we need to know our program in order to build the components we use to accelerate.

The third issue is the most important; to a first approximation, the first two are heuristics which help solve it. This intuition suggests an alternative framing as a statistical learning problem: you're given some training data in the form of pieces of program DFGs ($\mathcal G$), and the objective is to find a collection of snippets $\mathcal H$ that not only covers this program, but also can be re-configured to accelerate other programs in the future. We might imagine that there's some underlying distribution $\mathtt{Programs}$ of programs that people write, in which case the work we present here can be seen as a solution to the following optimization problem:

$$ \arg\max_{\mathcal H}\left( \mathop{\mathbb E}\limits_{\mathcal G\sim \texttt{Programs}}~ \mathcal S_{\mathcal H}(\mathcal G) - \text{Cost}(\mathcal H) \right)$$

where $\text{Cost}(\mathcal H)$ is the additional cost incurred by choosing to accelerate the subgraph stencil $\mathcal H$, which is higher for larger subgraphs. Note that in this presentation, we can no longer choose $\mathcal H$ based on $\mathcal G$, which resolves issue (3); issues (1) and (2) are partially incorporated into the $\text{Cost}(\mathcal H)$ term, effectively regularizing the search space by artificially imposing a cost for larger or more sub-graphs. Just like $\ell^1$ regularization, we are explicitly adding a preference for short descriptions, to avoid overfitting to a single program (like setting $\mathcal H:= \mathcal G$ as discussed above).

Rather than solve this optimization problem in closed form, we explicitly look for a given number of subgraphs (issue 1) and of a pre-selected size (issue 2). In doing so, we are using the regularization knobs to explicitly avoid over-fitting to the program at hand, which is necessary because our held-out evaluation (below) shows that generalizing to unseen programs is considerably more difficult.

Implementation strategy

We first instrument an LLVM module pass that writes out a JSON representation of the DFG. Our Python module then explores candidate subgraphs using a combination of our heuristics and the out-of-the-box graph isomorphism tooling.

We implemented and compared two separate algorithms for finding the stencils from static DFGs generated per-basic-block from LLVM programs.

In both cases, the general idea is to iterate over the DFG's connected components, successively building larger subgraphs. Our first approach is node-based, and exhaustively considers node subsets up to some size. The second approach is edge-based, and uses smaller subgraph components to build graphs of the desired size. In preliminary experiments we found the edge-based approach to be slightly faster, so we used that approach for our evaluation.

More specifically, the edge-based subgraph stencil generation iteratively grows connected subgraphs. For each $k$-edge subgraph in the DFG, the algorithm considers adding every edge in the DFG, keeping the new ($k+1$)-edge subgraphs that are connected. It then finds which of these subgraphs are isomorphic to each other, and constructs a canonical stencil name for each isomorphic set. These ($k+1$)-edge subgraphs are used for the next iteration of the algorithm.

Mutually exclusive matches

To generate a valid choice of subgraph stencils, we need more than simply an enumeration of all subgraphs in a program and a way to match them: we also have to make sure the matches don't step on one another's toes—that is, we need to throw out matches until each instruction is only covered by at most a single component.

Finding the optimal one is difficult: it is related to the weighted optimal scheduling problem (which can be solved with dynamic programming in $O(n \log n)$ time, but on a general directed graph, we get an exponential factor in the branching coefficient). Rather than solve this problem optimally in the general case, we implement the greedy biggest-first strategy, and focus instead on searching for collections of matches which have higher coverage in the first place.

After generating possible subgraph stencils, we choose a combination that achieves the highest static coverage of the DFG using only mutually exclusive matches.

Search

Ultimately, we do not need to search the space exhaustively if we have reasonable heuristics that might cause us to believe that we're going in the right direction with certain stencils. We can then do our search traversal in a different order, guided by the objective function. This can be done in the form of a beam search: we only keep around the $k$ best subgraphs in the search frontier, and at each step try to expand one to a random neighboring node. Though not used in our evaluation, beam search can speed up generating larger subgraphs in the future.

Evaluation

We primarily look at what coverage (percent of instructions matched by some subgraph over total instructions) we can get on a given source program. We consider both static and dynamic coverage. In both cases, 100% coverage is impossible because we exclude instructions with control-flow implications (phi, branch, return) and those that read and write from memory (load and store).

Dynamic coverage instrumentation

To generate dynamic coverage information, we instrument our LLVM pass. The pass adds annotation to each instruction that is matched specifying which stencil it was covered by, along with the node-isomorphism. Because basic blocks execute atomically (ignoring exceptions), we generate the count of matched and total instructions per-block at compile time. We then link a C profiling module with state for these dynamic counters. At the end of each basic block, our pass adds a call to a function to increment the profiling counters by the statically-determined amounts. We add a final function call to LLVM's global destructors list to write the final profiling values both to standard out and an auxiliary file. For convenience, we also save the static coverage the same way.

Embench evaluation

We chose to use the Embench embedded programming benchmarking suite because it represents a small but fairly diverse set of programs that can be easily compiled and executed with LLVM tooling.

For each benchmark, we generated all allowable three-node subgraphs and chose the two that statically covered the most instructions in that benchmark's DFG. Three-node stencil generation took between a few seconds and 17 minutes for each benchmark on a 2017 MacBook Pro (2.3 GHz Intel Core i5, 8 GB RAM).

The following graphs show static and dynamic code coverage for each benchmark. Note that each benchmark's coverage was calculated with the subgraphs generated from that benchmark (and coverages are deterministic, rendering error bars unnecessary).

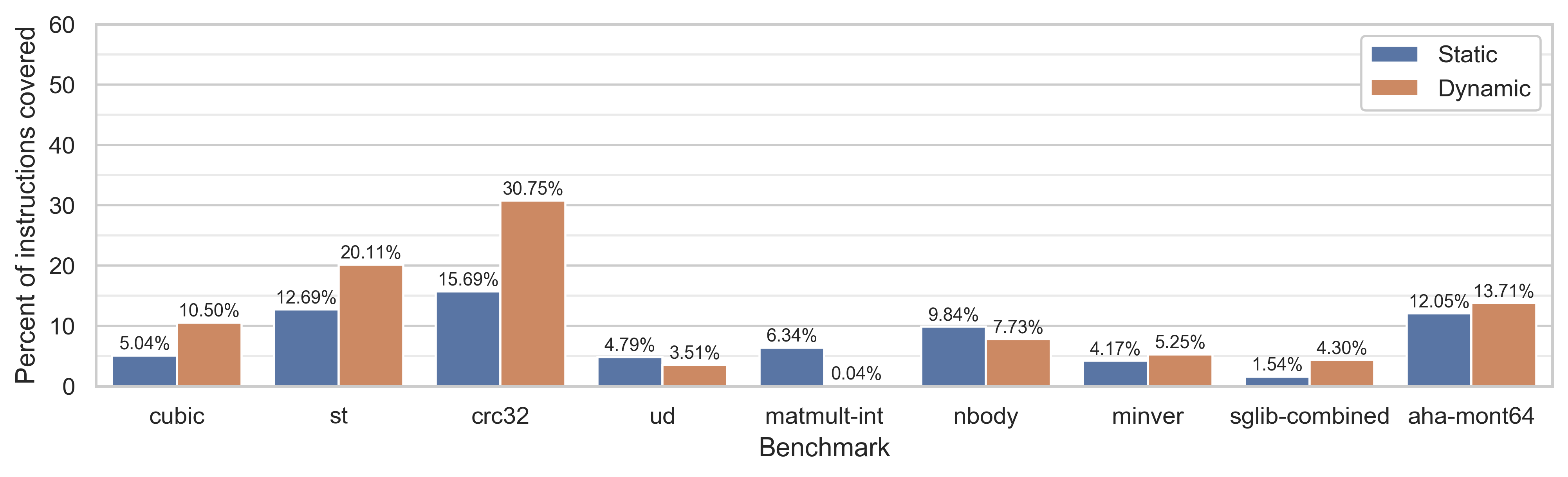
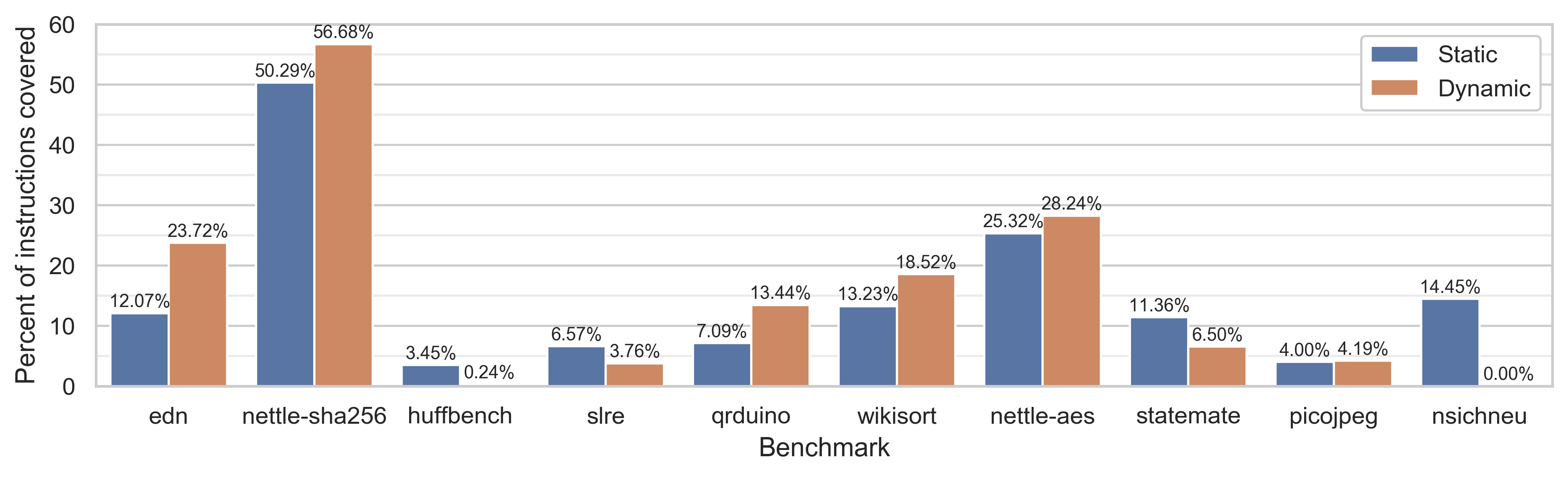
As stated above, a coverage of 100% is elusive because of our restrictions on what instructions we consider. An interesting component of this profiling data is that as expected, static and dynamic coverage correlate, but which is better depends on the particular benchmark. From smaller scale experimentation, the coverage also varies based on the compiler flags used to generate the original LLVM IR. In particular, running at a more aggressive -03 optimization level (rather than the -01 used here) changes the coverage metrics as loops are statically unrolled, introducing more redundancy.

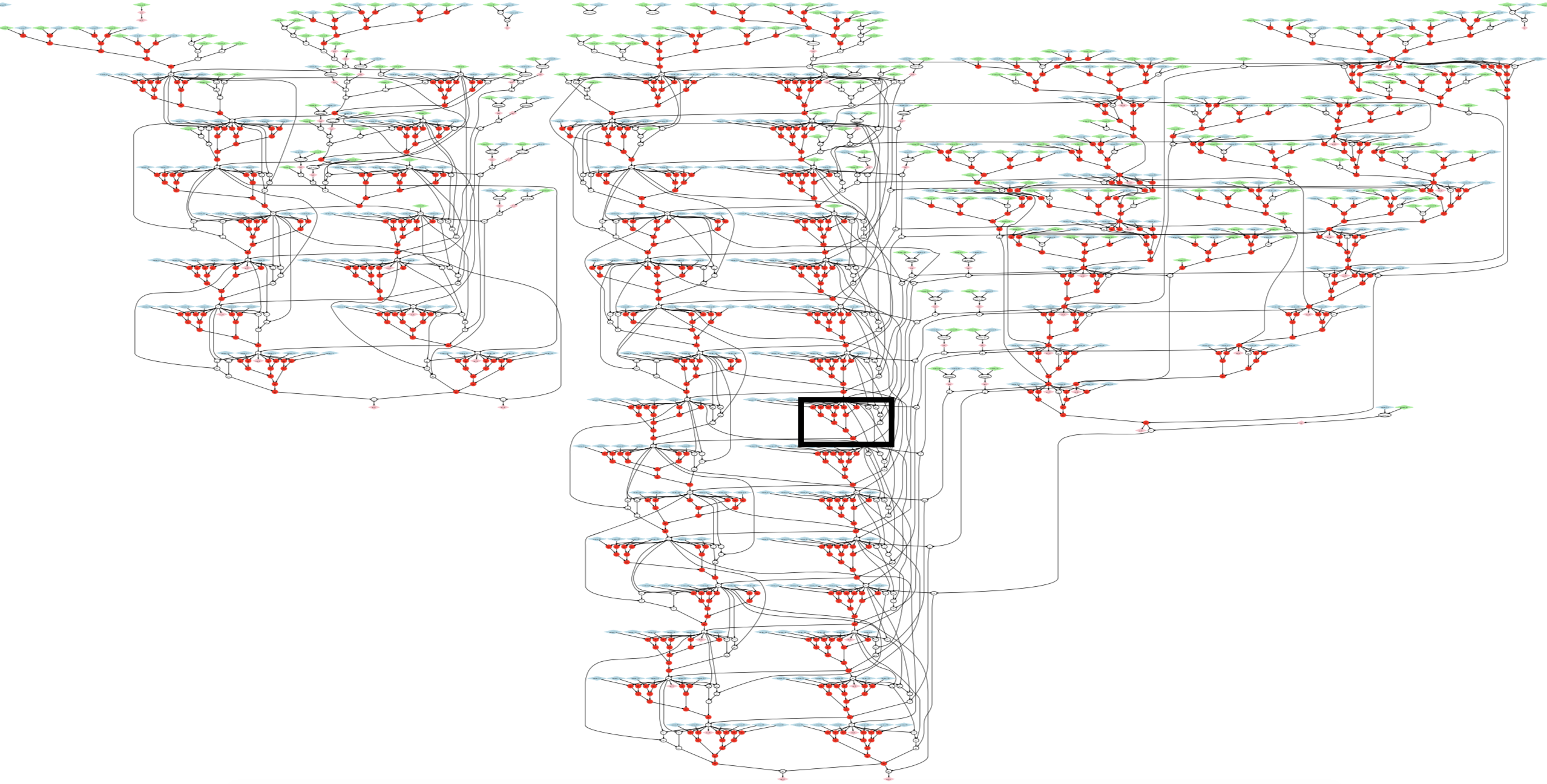
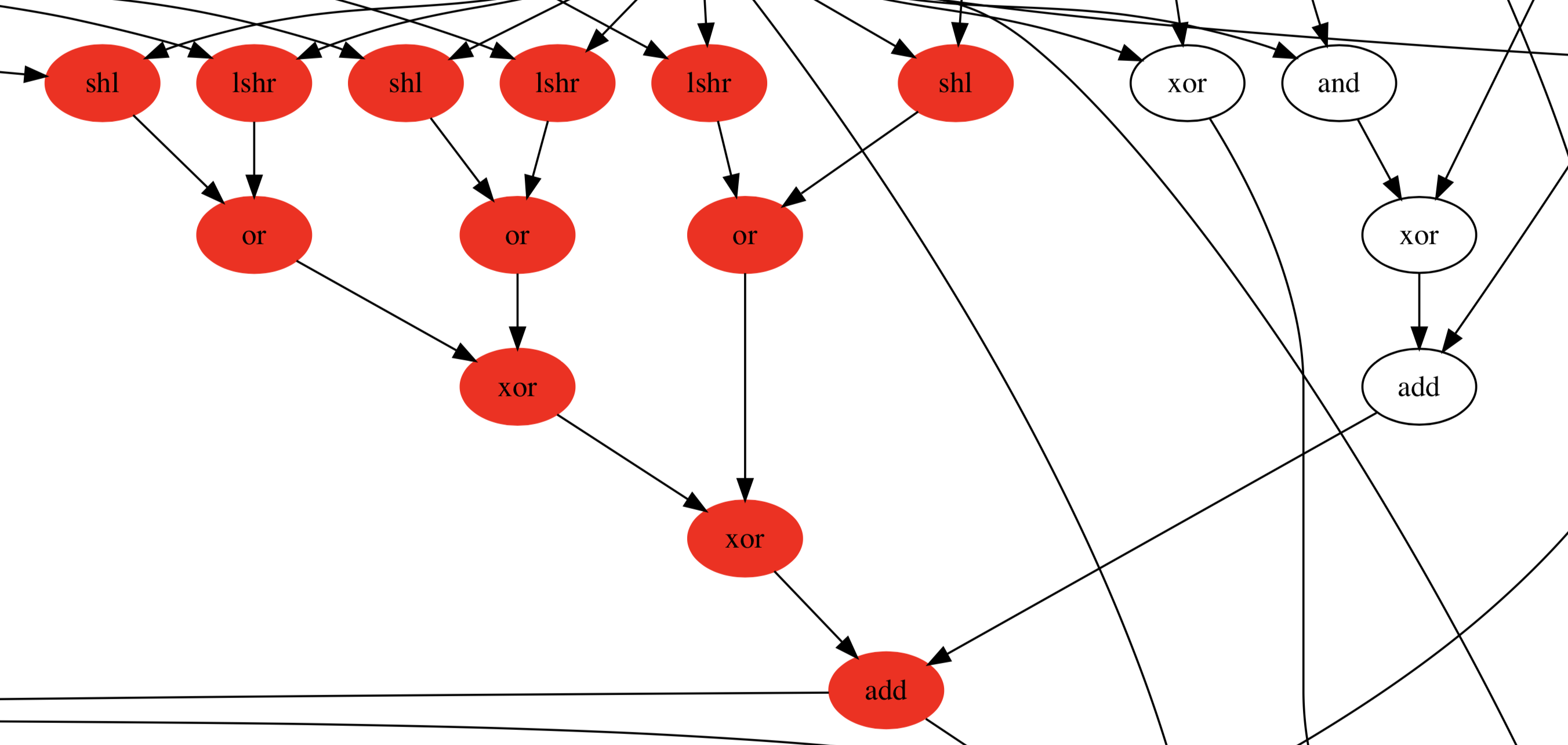
Embench case study: nettle-256sha

Digging into nettle-256sha, the benchmark with the best coverage, we can see that the following combination of three-node subgraph stencils was chosen out of 66 possible three-node subgraphs:

Here are a close-up and a closer-up (marked with a heavy black rectangle) view of the DFG, with vertices matched to a stencil shown in bright red. The latter shows three matches of the first stencil and one of the second.

Stencil generalization

We also explored generating stencils from one benchmark and testing how well they generalized to the other benchmarks. The three-node stencils generated and chosen from minver:

1. fcmp → select ← fsub
2. getelementptr ← pointer → getelementptr

were found at least once in all but five of the other Embench benchmarks, producing dynamic coverage ratios between 0 and 7.68% (with an average of 1.45% ± 2.35).

Stencils generated from other benchmarks achieved even less coverage on the rest of the benchmarks. For example, stencils generated from edn, libwiki, and nbody were not matched in any other benchmarks.

Ongoing directions

While finding redundancies in DFGs within each basic block is a good initial approach, this project could be extended in several directions.

We could build on existing literature in extended basic blocks to find subgraphs that speculatively occur. That is, in extended basic blocks, we consider control flows that are likely to jump from one block to another in the common case, and only fall back to different branches in the case that our guess of the next block was wrong. In the context of hardware acceleration, we can imagine building accelerators that handle these larger speculative subgraphs when possible, and fall back to slower CPU execution if the control flow differs.

In addition, it would be interesting to compare this project against dynamic data flow graphs. For example, the Redux paper essentially introduced the formulation of dynamic data flow graphs as we describe them here, and outlines how to efficiently generate them. From the perspective of hardware acceleration, the RADISH project (“Iterative Search for Reconfigurable Accelerator Blocks with a Compiler in the Loop”) uses Python wrappers to generate dynamic data flow graphs, and heuristic genetic algorithms to "fuse" similar dynamic graphs together.

Like RADISH, we could extend our application to target groups of applications instead of single programs. The scale of this undertaking would require more clever heuristics than our current search strategies, but would ideally help us find more general subgraphs to accelerate.

Finally, the impact of this project could be more clearly explicated by evaluating our subgraph identification with actual computational acceleration. In particular, we hope this strategy will prove useful in conjunction with other work that uses compile-time analysis for heterogeneous targets.