Instructions

High-Level Tasks

• Implement missing code in Mat2DH.ts
• Implement linear interpolation in SplineModel.ts (note that you will come back to this file later for the functions that deal with cubic bezier interpolation)
• Position and orient the car on the track to make it drive (in VehicleModel.ts)
• Implement Cubic Bezier interpolation in SplineModel.ts

caution

Before you begin, verify that you are able to run the starter code properly (see demo video on the setup page)

You will also want to read through the Anatomy of a Spline page before you proceed as well.

Part 1: Implement 2D Transformations with Homogeneous Coordinates

First, let's implement some convenience code to help us work in homogeneous coordinates. The file [Mat2DH.ts] for building 3x3 matrices that represent common 2D transformations in homogeneous coordinates. We will focus on translation, rotation, and scale.

For this, you will need to use the Vec3 and Mat3 classes to represent 2D geometry and transforms in homogeneous coordinates.

Mat2DH.ts Tasks

• Implement _Vec2DH(x:number, y:number):Vec3, which should take a Vec2 and return a Vec3 representing the corresponding 2D vector in homogeneous coordinates
• Implement _Point2DH(x:number, y:number):Vec3, which should take a Vec2 and return a Vec3 representing the corresponding 2D point in homogeneous coordinates
• Implement Mat2DH._Scale2D(scaleX:number, scaleY:number):Mat3 which should take separate scale values for x and y dimensions, and return the corresponding 3x3 scale matrix for 2D homogeneous coordinates
• Implement Mat2DH._Translation2D(x:number, y:number):Mat3 which should take separate offset values for x and y dimensions, and return the corresponding 3x3 scale matrix for 2D homogeneous coordinates
• Implement Mat2DH.Rotation2D(radians:number):Mat3 which should take an angle expressed in radians and return the corresponding 3x3 (counter-clockwise) rotation matrix for 2D homogeneous coordinates

How to test:

There are two ways to check your work here. The first is unit tests; we have provided some to get you started, but you may want to write some more of your own to make sure your implementation is robust. The second way is to see what happens when you apply a matrix to a car. When you press v ir b while running the demo, a VehicleModel repesenting a car will be added to the scene. The update(currentTime:number) function defined in VehicleModel.ts will then be called to update the car each frame. Eventually, you will write this function so that the car drives along a track. But, for now, you can use it to test out your Mat2DH.ts functions.

Part 2: Counting Spline Properties

If you haven't already, read through the Anatomy of a Spline page. Then, fill in the getters listed below for SplineModel. Note that get nControlPoints():number is provided for you.

SplineModel.ts Tasks

• Implement get nInterpolatedControlPoints():number, which returns the number of interpolated control points in the current spline if we interpret the control points as defining a cubic Bezier spline.
• Implement get nBezierSegments():number, which returns the number of bezier segments.
• Implement continuousSegmentIndexForProgress(progress:number):number, which maps global progress along the complete spline to an index, with the integer part referring to the current segment index and the decimal part indicating progress along that segment.
• Implement getControlPointIndexForInterpolatedControlPoint(interpolatedControlPointIndex:number):number, which returns the control point index of the interpolatedControlPointIndex'th interpolated control point.

Try running the Assignment tests at this point to see if you pass any tests that cover these functions.

Part 3: Linear Interpolation

Next we will implement linear interpolation. By the end of this step, our track should take on the shape of our control polygon. You will implement linear interpolation for both the position of the spline and for the color of the spline. The functions getControlPointLocation(index:number):Vec2 and getControlPointColor(index:number):Color may prove useful here if you would prefer not to deal directly with the model's vertex array.

SplineModel.ts Tasks

• Implement getLinearInterpolationPoint(progress:number):Vec2
• Implement getLinearInterpolationColor(progress:number):Color

Below is a demo of what things look like after you have completed linear interpolation. You should be able to draw linear tracks now, and you can change the colors of those tracks, but cars will still just spawn in the center of the screen:

Part 4: Smooth Spline Interpolation

Now we want to use cubic Bezier splines to make our roads smooth. Refer to Anatomy of the Spline for a refresher if you need it. You will need to implement code in both CubicBezierFunctions.ts and SplineModel.ts.

NOTE: You can choose to implement function GetSplineSegmentValueForAlphaAndMatrix(...), which can be used to implement the other functions in CubicBezierFunctions.ts more compactly. This is optional; you can also choose implement the other functions with vector operations (e.g., .plus() and .times()).

CubicBezierFunctions.ts Tasks

• Implement function GetCubicBezierSplineSegmentValueForAlpha

SplineModel.ts Tasks

• Implement getCubicBezierInterpolationPoint(progress:number):Vec2
• Implement getCubicBezierInterpolationColor(progress:number):Color

Part 5: Putting Cars on the Road

The next step will be to put the cars on the track. For this, we will use the awesome power of homogeneous coordinates.

To position and orient cars, edit the update(currentTime:number) function in VehicleModel.ts. For starters, we recommend just trying to position the car on the track. If you have implemented the previous steps correctly, you will want to center the origin of the car's coordinate system at the point returned by getPositionForTime(currentTime). Next try to scale the car according to vehicleModel.scale. If you are doing these correctly, you should get some sick sideways drifting behavior:

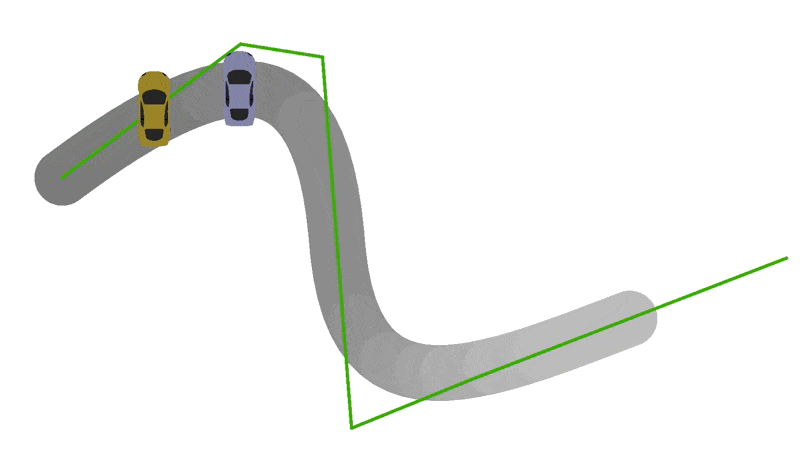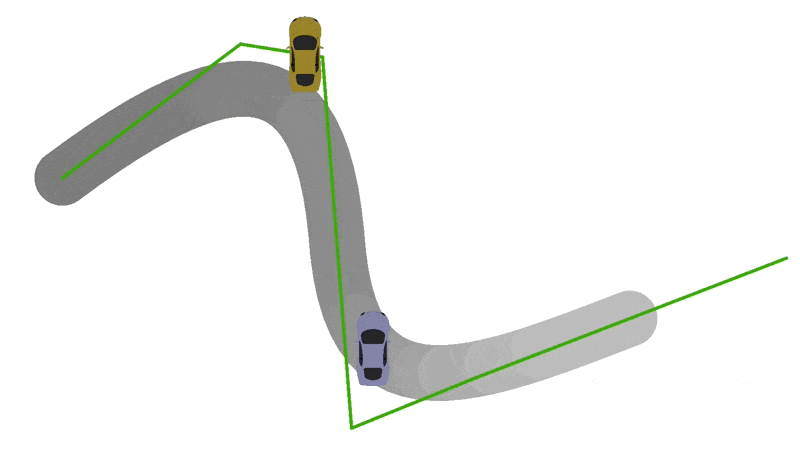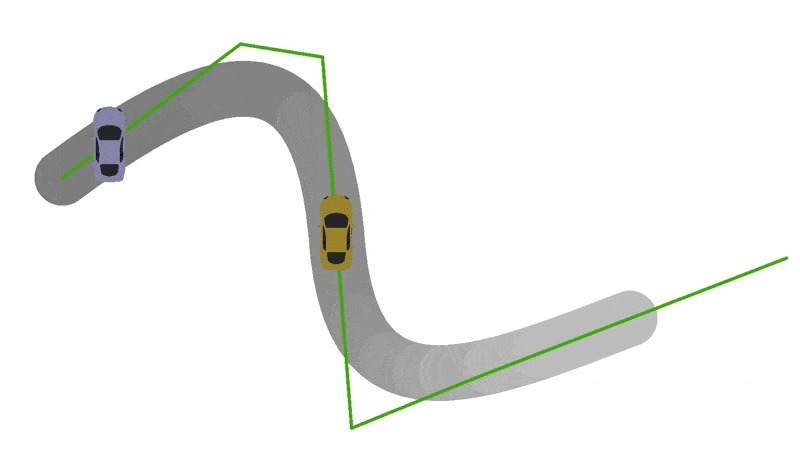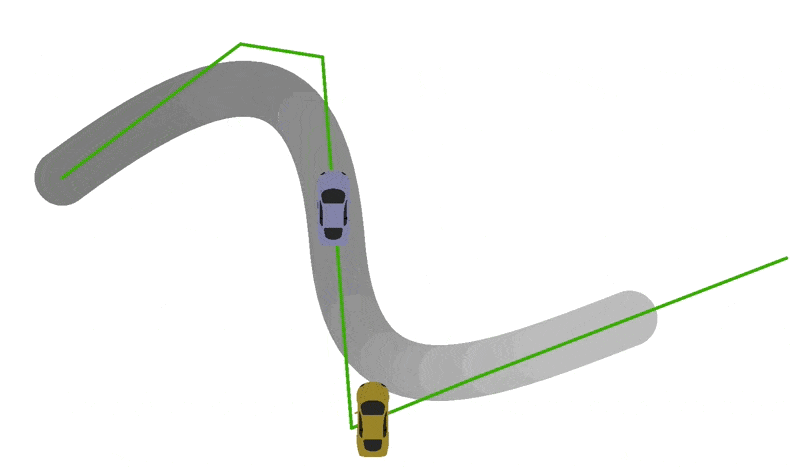
Part 5: Vroom Vroom...

Now for the final step: getting the cars to point forward. We need orient each car so that its front (for our car model, the positive y-axis) points in the direction it is driving. To do this, we will have to calculate the velocity vector for each car, which we can do by differentiating our spline curves with respect to spline progress. Specifically, we will calculate the derivatives of our curves with respect to the alpha parameters of each segment.

First, complete the function getLinearInterpolationVelocity(progress:number):Vec2, which should calculate the velocity vector for the linearly interpolated path. Linear interpolation will not usually be differentiable at vertices of the control polygon, so behavior there may be undefined. For these points, just make sure you return a valid unit vector pointing in some direction.

At this point, you can go back to the update(currentTime:number) function in VehicleModel.ts and orient your cars so that they point in the direction returned by getVelocityForTime. They should

Finally, complete the function getCubicBezierVelocityVector(progress:number):Vec2. For this, you will need to find the derivative of a cubic Bezier segment with respect to its alpha parameter. Remember that we can express these segments as cubic polynomial functions of alpha. You will want to take the derivative of that polynomial with respect to alpha to find the velocity.

CubicBezierFunctions.ts Tasks

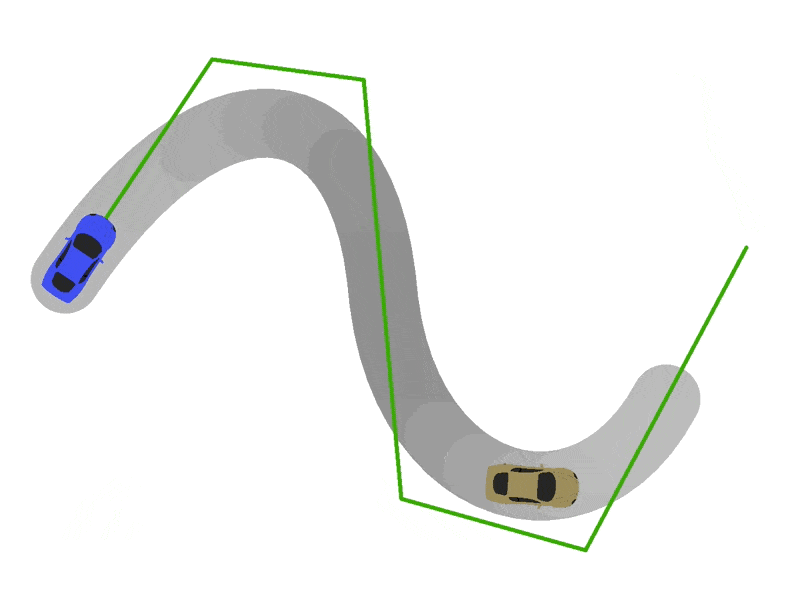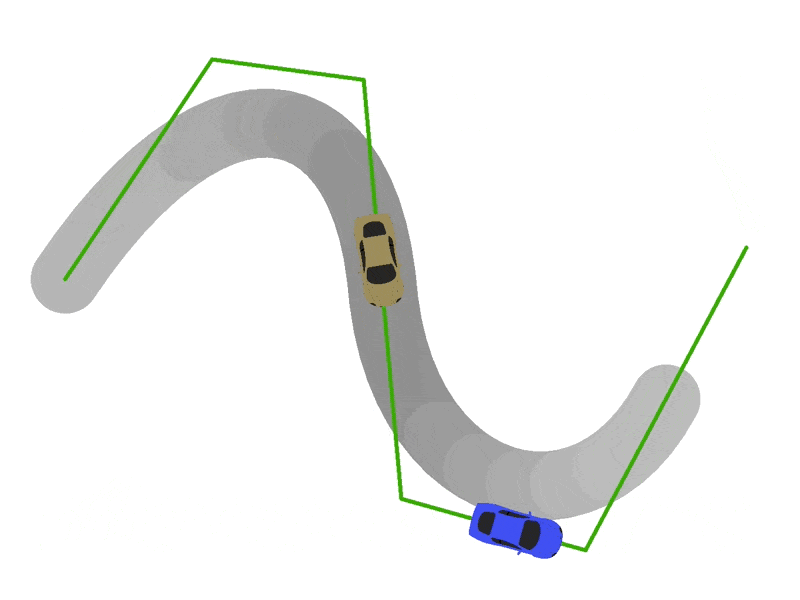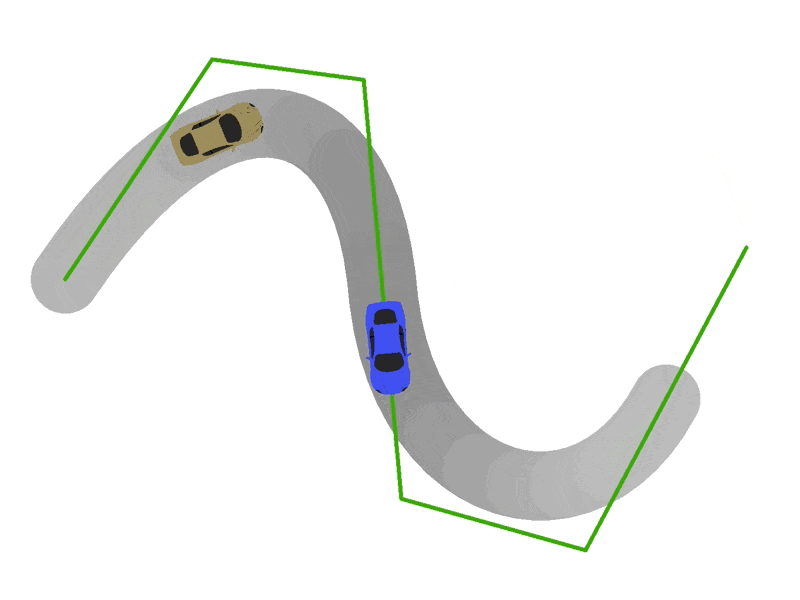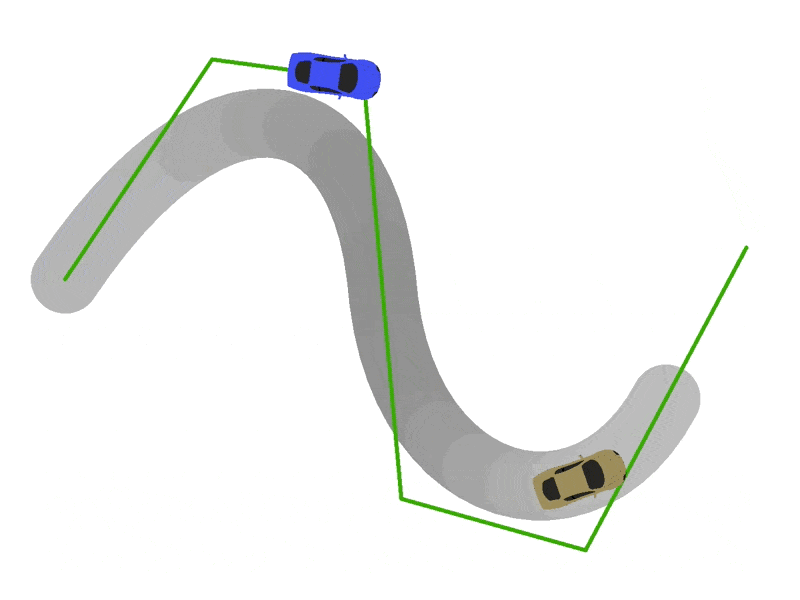
• Implement function GetCubicBezierSplineSegmentDerivativeForAlpha

SplineModel.ts Tasks

• Implement getLinearInterpolationVelocity(progress:number):Vec2
• Implement getCubicBezierVelocityVector(progress:number):Vec2

VehicleModel.ts Tasks

• Finish update(currentTime:number)