CS 4120: Introduction to Compilers
Fall 2013

Problem Set 5: Program Analysis and Advanced Language Features

due: Tuesday, November 26, 11:59PM - No Late Days!

1. Bounding intervals

   We want to design a dataflow analysis that computes conservative intervals bounding the values of all integer variables. An analysis along these lines could be used for eliminating bounds checks, for example. We extend the set Z of integers with plus and minus infinity: Z^* = Z ∪ {+∞, -∞}, such that -∞ < n, and n < +∞ for any integer n. We then define a preorder over the set L = {[a, b] | a, b ∈ Z^* ∧ a ≤ b} ∪ {⊥}.

   1. Explain what the element ⊥ represents and why we need it for this analysis. Define the preorder and the join operator for elements in this preorder (including ⊥).
   2. Using this preorder to compute ranges of variables will fail in general. Explain why.
   3. To solve the problems from part (b), we define a preorder L′ = {[a, b] | a, b ∈ {∞, -k, ..., k, +∞} ∧ a ≤ b } ∪ {⊥} (with the same preorder as before, and for some constant k, and build a dataflow analysis that computes ranges in L′ . Show the flow functions for the following nodes:
      • assignment to a constant x := n;
      • addition x := y + z;
      • multiplication x := y * z;
   4. This is an example of an analysis where it makes sense to propagate different information along different out edges from a node. Give a suitable flow function for each of the out edges of a comparison x < n, and show that with this analysis we can derive a bound [10, 10] for variable i at the exit from the following example:

      i := 0;
      while (i < 10) {
          i := i + 1;
      }
      

2. Defending against zombies with dataflow analysis

   Let us define "undead" code as code that depends on a variable that is always uninitialized. When such undead code is removed, additional program regions may become undead due to the disappearance of variable declarations. The goal of this exercise is to remove all undead code from a function using only a single analysis pass.

   1. Design a dataflow analysis that can be used for cascading undead-code removal. Describe its preorder, the join operator, the bottom element, as well as the flow function. Where necessary, be conservative. You only need to specify the flow function for assignments x:=expr;.
   2. Show that the flow functions you defined are monotonic, and either show that they preserve joins or construct a counterexample.
   3. Show that one run of your analysis leads to the removal of the following grayed-out undead code (remember that joins are used at merge points in the CFG):
      1. a := 1;
      2. if (f(a) > 0) {
      3.   c := c+1;
      4.   d := 5;
      5. }
      6. d := a+c;
      7. g := a+d;
3. Object layout

   Consider the following class declarations in a Java-like language with subtyping, inheritance, and method overriding, but with a simple type hierarchy in which no class has two parents:

   class A {
       int a;
       int f() { code 1 }
   }
   
   class B extends A {
       int b;
       int f() { code 2 }
       int g() { code 3 }
       int h() { code 4 }
   }
   
   class C extends A {
       int c;
       int f() { code 5 }
       int j() { code 6 }
       int g() { code 7 }
   }
   

   Using vtables with sequentially assigned method indices (i.e. indices for methods introduced by inheriting classes start after last index for methods introduced by inherited classes), draw the memory layout of instances of classes A, B, and C, including the objects themselves, their vtables and the code for all their methods. Here there is only single inheritance, so there is no need for an interface table.

   Now, suppose instead that the language supports multiple inheritance of interfaces and we had the following:

   interface A {
       int a();
   }
   interface B {
       int b();
   }
   interface C {
       int c();
   }
   class X extends C, B {
       int c() { code 1 }
       int x() { code 3 }
       int b() { code 2 }
   }
   class Y extends X, A {
       int y() { code 4 }
       int x() { code 5 }
       int a() { code 6 }
   }
   class Z extends A, C {
       int a() { code 7 }
       int c() { code 8 }
   }
   

   Assuming the language implementation is based on vtables and interface tables with offsets, draw the memory layout of instances of classes X, Y, and Z, including the objects themselves, their vtables and interface tables, and the code for all their methods.

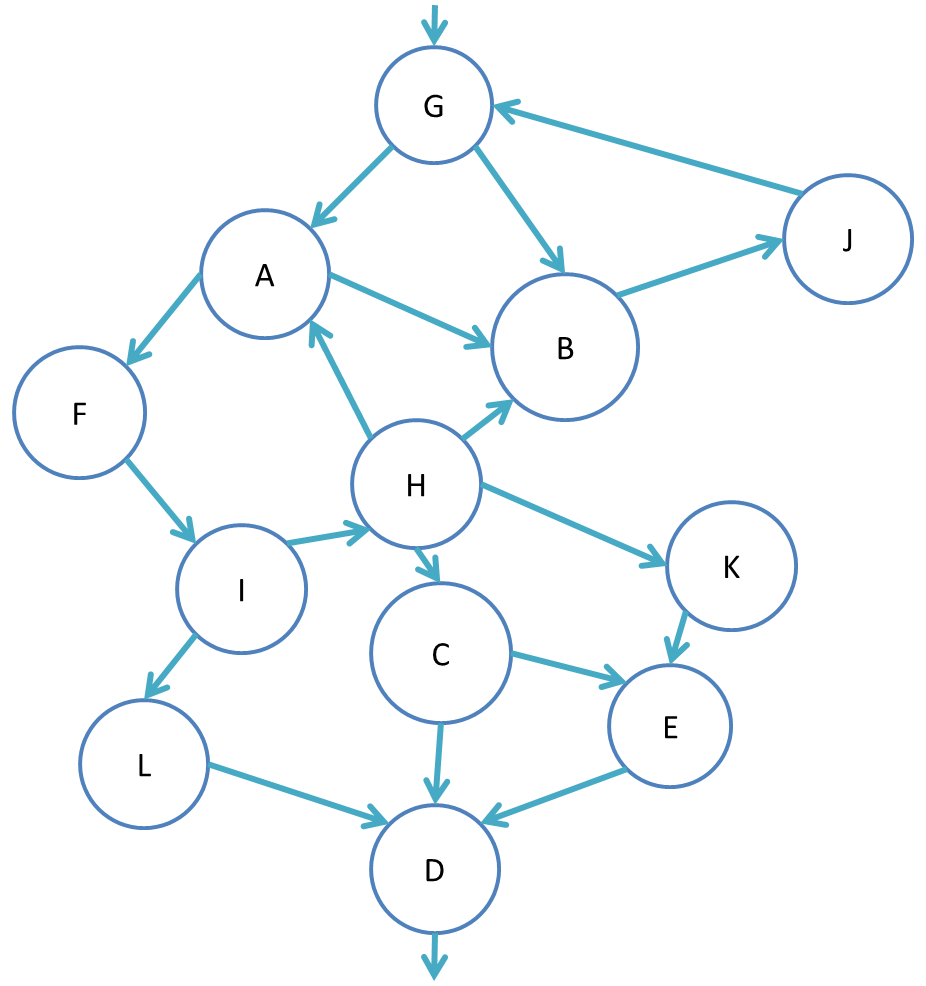
4. Control-Flow Analysis (CS 5120 only)

   For the following control-flow graph, present the dominator tree (plus back edges shown in dashed), identify the loops and the control tree, and for each loop indicate its set of nodes, its header node, and its exit edges: