Crowdsampling the Plenoptic Function


Crowdsampling the Plenoptic Function
ECCV 2020
Learning the Depths of Moving People by Watching Frozen People


Learning the Depths of Moving People by Watching Frozen People
CVPR 2019
Learning Material-Aware Local Descriptors for 3D Shapes
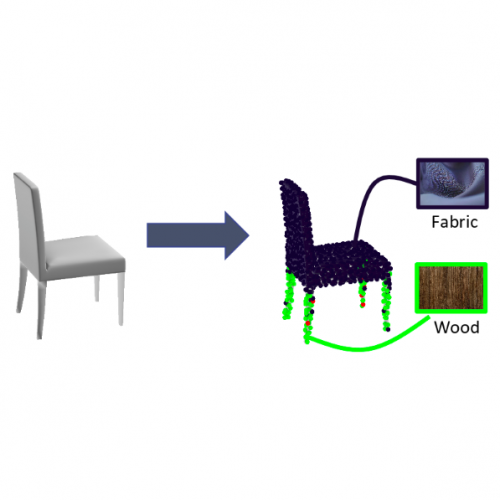

Learning Material-Aware Local Descriptors for 3D Shapes
3DV 2018
MegaDepth: Learning Single-View Depth Prediction from Internet Photos


MegaDepth: Learning Single-View Depth Prediction from Internet Photos
CVPR 2018
Low-shot Learning from Imaginary Data


Low-shot Learning from Imaginary Data
CVPR 2018
Animating Elastic Rods with Sound


Animating Elastic Rods with Sound
SIGGRAPH 2017
