Chapter 10 Mechanism Design and Auctions

In our earlier study of matching markets, we demonstrated that market-clearing prices exist and that the market can adjust its prices over time to reach them. We now turn to a “single-shot” version of this problem: We still have a set of buyers and a set of items for sale, but this time we consider a situation where the sale of the items is being administered by a central entity (“the auctioneer”) as opposed to it happening in a decentralized way in a market.

We are interested in studying mechanisms that such an auctioneer can use to assign items to buyers in a way that maximizes social value (and thus, by Corollary 8.1, also social welfare). (As an aside, in many situations the auctioneer may also be the seller of the items [e.g., in the context of Google selling advertising slots]; in such situations, the auctioneer may instead want to choose a mechanism that maximizes their own revenue rather than social welfare. This leads to a separate question that can be considered in the same framework. We here focus on “ideal” mechanisms adopted by a “benevolent” auctioneer and thus only consider social value maximization.)

To enable the mechanism to find an assignment that maximizes social value, the buyers need to report their valuations to the mechanism. An issue that arises here is that buyers may be trying to “game the system” and misreport their valuations in order to get a more advantagous assignment. The mechanism must appropriately set prices so as to incentivize the buyers to truthfully report their valuations.

To consider this question, and generalizations of it, let us begin by introducing a general framework for mechanism design.

10.1 The Mechanism Design Model

Consider a scenario where we have:

A set of

n

players.

A finite set of states

Ω

from which the mechanism will select the one. (For instance, in the case of matching markets, the state

ω \in Ω

will specify an allocation of items to buyers.)

T = T_{1} \times T_{2} \times \dots \times T_{n}

is the product of sets

T_{i}

; we refer to

T

as the type space, and

T_{i}

as the type space for player

i

. Intuitively, the type

t_{i} \in T_{i}

of a player describes the “personality” of a player. (For instance, in the case of matching markets, the type of a player specifies the player’s value for each item.)

Each player $i$ is also associated with a valuation function $v_{i} : T_{i} \times Ω \to ℕ$ , where $v_{i} (t_{i}, ω)$ describes how a player $i$ having type $t_{i} \in T_{i}$ values a state $ω \in Ω$ . (For instance, in the case of matching markets, $v_{i}$ is a function which uses $ω$ to determine which item player $i$ gets, and then uses $t_{i}$ to determine $i$ ’s value for the item.)¹

We refer to such a tuple $(n, Ω, T, \vec{v})$ as a mechanism design context, or simply a context.

Let us now consider the following process induced by a mechanism $ℳ$ :

Each player $i$ submits a “report” $r_{i} \in T_{i}$ to the mechanism $ℳ$ . Ideally, the players submit their true type—that is, $r_{i} = t_{i}$ —but players need not necessarily be “truthful.”
$ℳ (\vec{r})$ outputs a state $ω \in Ω$ and a profile of prices/payments $\vec{p} \in ℝ^{n}$ ; we refer to the tuple $(ω, \vec{p})$ as the outcome.
The utility of a player $i$ with type $t_{i}$ in an outcome $(ω, \vec{p})$ is defined as: $u_{i} (t_{i}, ω, \vec{p}) = v_{i} (t_{i}, ω) - p_{i} .$

In other words, player $i$ receives as utility its value of the outcome $ω$ minus the payment $p_{i}$ it is charged by the mechanism. This type of a utility function is referred to as a quasi-linear utility function: note that it generalizes the utility function used in our study of matching markets.²

To better understand the notion of a context and the above-described process, let us consider some basic examples, starting with the concept of an auction.

First- and Second-price auctions Consider the following setting:

We have a set of $n$ buyers, and a single item for sale.
The states $Ω = [n] \cup ⊥$ determine which of the $n$ players will receive the object (where $⊥$ represents no player winning).
Player $i$ ’s type $t_{i} \in T_{i} = ℕ$ describes $i$ ’s valuation for the object.
The valuations function $v_{i} (t_{i}, ω) = t_{i}$ if $ω = i$ (i.e., $i$ gets the object) and 0 otherwise.³

We refer to a context $Γ = (n, Ω, T, \vec{v})$ as above as a single-item auction context.

Now, consider the following first-price auction mechanism $ℳ$ for any such single-item auction context: The mechanism $ℳ$ —run by the auctioneer, upon receiving reports (i.e., bids) $r_{i} \in ℕ$ from each player $i$ —returns $ℳ (\vec{r}) = (i^{*}, \vec{p})$ , where:

$i^{*} = arg max_{i} r_{i}$ (i.e., the winner is the player who bids the highest value); in the case of ties, break ties lexicographically (i.e., according to their player identities, so that player 1 gets precedence over player 2 who gets precedence over player 3 and so on).
$p_{i} = 0$ if $i \neq i^{*}$ (i.e., only the winner should pay for the item).
$p_{i^{*}} = r_{i^{*}}$ (the winner should pay the amount that they bid).

We can similarly define a second-price auction, where the winner is still the highest bidder, but they instead need only pay the second-highest bid; that is,

p_{i^{*}} = max_{j \in [n] ∖ i^{*}} r_{j} .

10.2 Goals of Mechanism Design

The goal of mechanism design is to, given some context $Γ = (n, Ω, T, \vec{v})$ , design a mechanism $ℳ$ for this context that ensures that “rational play” leads to some “desirable” outcome, no matter what types the players have.

Desirability of outcomes As mentioned above, in our study of mechanism design, the notion of desirability will be to maximize social value (but as mentioned, other notions of desirability are also useful—for instance, in the setting of an auction, we may consider the notion of maximizing the seller’s revenue). Given a context $Γ$ , let the social value be given by

S V^{Γ} (\vec{t}, ω) = \sum_{i \in [n]} v_{i} (t_{i}, ω) .

Given a context $Γ = (n, Ω, T, \vec{v})$ and a type profile $\vec{t} \in T$ , we say that a state $ω$ maximizes social value with respect to $Γ$ and $\vec{t}$ if

ω = arg max_{ω^{'} \in Ω} S V^{Γ} (\vec{t}, ω^{'}) .

We additionally say that an outcome $(ω, \vec{p})$ maximizes social value if $ω$ maximizes social value.

We can also define social welfare as we did in chapter 8 by additionally incorporating the prices paid by the players as well as the profit made by the mechanism operator (e.g., the “seller” in the setting of an auction); by the same argument as in Claim 8.1, these prices will cancel out with the mechanism operator’s profit, and so social welfare will be equal to social value.

Rational play and truthful implementation Let us now turn to defining what we mean by “rational play.” Several interpretations of this are possible. Ideally, we would like to have a mechanism where “rational” players will truthfully report their types. For instance, in an auction, this would mean that players truthfully submit their actual valuations to the auctioneer (and do not attempt to manipulate the mechanism). To formalize this using notions from game theory, we must first view the process as a game: Given a context $Γ = (n, Ω, T, \vec{v})$ a type profile $\vec{t} \in T$ , and a mechanism $ℳ$ , let $𝒢^{Γ, \vec{t}, ℳ}$ denote the game induced by $Γ, \vec{t}$ , and $ℳ$ , where each player $i$ chooses some report $r_{i}$ (as their action) and their utility is defined as above, based on the state and prices ultimately chosen by $ℳ (\vec{r})$ . (More precisely, the actions space for each player $i$ is $T_{i}$ and the utility $u^{'}$ for player $i$ is defined as $u_{i}^{'} (\vec{r}) = v_{i} (t_{i}, ω) - p_{i}$ where $(ω, \vec{p})$ is the output of $ℳ (\vec{r})$ .)

We now have the following natural notion of what it means for a mechanism to be truthful.

Definition 10.1. A mechanism $ℳ$ is dominant-strategy truthful (DST) for the context $Γ = (n, Ω, T, \vec{v})$ if, for every $\vec{t} \in T$ , $t_{i}$ is a dominant strategy for player $i$ in $𝒢^{Γ, \vec{t}, ℳ}$ .

So, if $ℳ$ is DST, then players are incentivized to report their true type (e.g., for auctions, their true valuation of the object) regardless of what other players choose to do! This is a relatively strong notion of truthful implementation; we may also consider a seemingly weaker notion, which simply requires that the action profile where all players truthfully report their types is a Nash equilibrium:

Definition 10.2. A mechanism $ℳ$ is Nash truthful (NT) for the context $Γ = (n, Ω, T, \vec{v})$ if, for every $\vec{t} \in T$ , $\vec{t}$ is a Nash equilibrium in $𝒢^{Γ, \vec{t}, ℳ}$ .

As it turns out, these notions are equivalent:

Claim 10.1. A mechanism $ℳ$ is DST if and only if it is NT.

Proof. If $ℳ$ is DST, then it is clearly NT. Conversely, let us assume for the sake of contradiction that $ℳ$ is NT and not DST; that is, there exist some types $\vec{t}$ , some player $i$ and reports $r_{- i}$ , such that $t_{i}$ is not a best response with respect to $r_{- i}$ assuming players have the types $\vec{t}$ . We then claim that $t_{i}$ is not a best response with respect to $r_{- i}$ assuming players have the types $(t_{i}, r_{- i})$ —this directly follows from the fact that the utility function of player $i$ only depends on $i$ ’s valuation and payment and is independent of other players’ types. It follows that $ℳ$ is not NT since $i$ wants to deviate given the types ${\vec{t}}^{'} = (t_{i}, r_{- i})$ , which is a contradiction.

■

Given the notion of DST, we can now define what it means for a mechanism to implement social value maximization.

Definition 10.3. A mechanism $ℳ$ is said to DST-implement social value maximization for the context $Γ = (n, Ω, T, \vec{v})$ if $ℳ$ is DST for $Γ$ and, for every $\vec{t} \in T$ , $ℳ (\vec{t})$ maximizes social value with respect to $Γ$ and $\vec{t}$ .

Nash implementation We may also consider a weaker notion of implementation, which we refer to as Nash implementation (in contrast to Nash-truthful implementation). This notion only requires the existence of some social value maximizing PNE; this PNE need not, however, be truthful (as in the notion of Nash-truthful implementation).

Definition 10.4. A mechanism $ℳ$ is said to Nash-implement social value maximization for the context $Γ = (n, Ω, T, \vec{v})$ if, for every $\vec{t} \in T$ , there exists a PNE $\vec{t^{'}}$ for $𝒢^{Γ, \vec{t}, ℳ}$ such that $ℳ (\vec{t^{'}})$ maximizes social value with respect to $Γ$ and $\vec{t}$ .

Revisiting the first- and second-price auctions Let us now examine whether the examples of first-price and second-price auctions satisfy our desiderata. Clearly, the simple first-price auction is not truthful; if everyone else values an object at 0, and you value it at 100, you would clearly be better off bidding something less than your actual value (say, 1), thereby saving a lot of money buying the item! Generally, bidding your true value always provides a utility of 0 (since you pay what you bid), so underbidding can never be worse. However, for the second-price auction, we have the following beautiful result.

Theorem 10.1. The second-price auction mechanism DST-implements social value maximization.

Proof. We start by showing that the second-price auction is DST. By Claim 10.1, it actually suffices to show that it is NT, which we now show.

Consider some type (i.e., valuation) profile $\vec{t}$ . We need to show that $\vec{t}$ is a PNE. Consider some player $i$ with valuation $t_{i}$ , and let $t^{*}$ be the highest valuation of all the players, excluding $i$ ; that is:

t^{*} = max_{j \neq i} t_{j} .

First, note that by bidding $t_{i}$ (i.e., by bidding truthfully), player $i$ can never end up with negative utility—either the bid is losing (and he gets 0 utility) or he gets the item for the second highest bid, which is at most $t_{i}$ . We next argue that $i$ cannot improve their utility by either overbidding (bidding above $t_{i}$ ) or underbidding (bidding below $t_{i}$ ), by considering the following cases:

Case 1: $t_{i} < t^{*}$ . As long as $i$ bids below $t^{*}$ (or at $t^{*}$ while losing the tie-break), his utility remains 0. In contrast, if he bids above $t^{*}$ (or at $t^{*}$ while winning the tie-break), his utility becomes negative—he needs to pay $t^{*}$ for an item that he values at $t_{i} < t^{*}$ .

Case 2: $t_{i} > t^{*}$ . As long as $i$ bids above $t^{*}$ (or at $t^{*}$ while winning the tie-break), his utility remains unchanged—he still needs to pay $t^{*}$ . In contrast, if $i$ bids below $t^{*}$ (or at $t^{*}$ while losing the tie-break), his utility becomes 0.

Case 3: $t_{i} = t^{*}$ . If $i$ loses the auction his utility is 0, and if he wins, he needs to pay $t^{*} = t_{i}$ , so again his utility is 0.

Thus, $\vec{t}$ is a PNE, and so the second-price auction is NT and thus also DST. Finally, by construction, if everyone bids truthfully, then the player (or one of the players, in the case of ties) who values the item the most will win the auction; thus, the auction chooses an outcome that maximizes social value.

■

First-price auctions, while not truthful, still turn out to Nash-implement social value maximization.

Theorem 10.2. The first-price auction mechanism Nash-implements social value maximization.

Proof. Given any type (valuation) profile $\vec{t}$ , let $i^{*}$ be the player (or in the case of ties, the player with the smallest identity) with the highest valuation; in other words, $i^{*}$ is the player that would have won the auction if everyone were to bid truthfully. Let $t^{* *}$ be the “second-highest” valuation; that is,

t^{* *} = max_{i \in [n] ∖ i^{*}} t_{i},

and let $I^{* *}$ be the set of players having valuation $t^{* *}$ . We consider two cases:

Case 1: For all

i \in I^{* *}

i^{*} < i

. That is,

i^{*}

would win a tie-break against everyone in

I^{* *}

. In this case, consider the bids

r_{i} = t_{i}

i \neq i^{*}

and

r_{i^{*}} = t^{* *}

(i.e., the player with the highest valuation bids the second highest valuation, and everyone else bids their true valuation). We aim to show that

\vec{r}

is a PNE. First, note that if everyone plays

\vec{r}

, then due to the tie-break, player

i^{*}

will win the auction and pay price

t^{* *}

. Next, note that by deviating, players other than

i^{*}

can never increase their utility as they would need to pay at least

t^{* *}

for the item. Meanwhile,

i^{*}

(who wins the item if everyone plays

\vec{r}

) loses utility by bidding above

t^{* *}

, and receives 0 (losing the item) by bidding below

t^{* *}

. We conclude that

\vec{r}

is a PNE.

Case 2: There exist some $i^{* *} \in I^{* *}$ such that $i^{* *} > i^{*}$ . That is, $i^{*}$ would lose a tie-break against some $i^{* *} \in I^{* *}$ . Note that in this case, $i^{*}$ must be the unique player with the highest valuation (since by definition they wins all tie-breaks against players having the same valuation), and thus $t_{i^{*}} > t^{* *}$ . Consider the bids $r_{i} = t_{i}$ if $i \neq i^{*}$ and $r_{i^{*}} = t^{* *} + 1$ . Again, note that if everyone plays $\vec{r}$ , then player $i^{*}$ will clearly win the auction (since they bid strictly higher than everyone else) and will pay price $t^{* *} + 1 \leq t_{i^{*}}$ (since valuations are integers). As before, players besides $i^{*}$ can never increase their utility as they would need to pay at least $t^{* *} + 1$ for the item. $i^{*}$ (who wins the item if everyone plays $\vec{r}$ ) still loses utility by overbidding; additionally, player $i^{*}$ will still receive 0 (losing the item) by underbidding, since by assumption player $i^{*}$ will lose the tie-break if they bid $t^{* *}$ .

So in either case $\vec{r}$ is a PNE. Additionally, in both cases, since the object is assigned to the player who values it the most, the auction also implements social value maximization. (Perhaps surprisingly, notice that in this Nash equilibrium the pricing is essentially identical to that in a second-price auction: the player with the highest valuation either bids the second-highest valuation or just slightly above it.)

■

Nash-implementation vs. DST implementation Notice that in the case of a first-price auction, in order for the players to figure out what the Nash equilibrium strategy actually is, they need to know each others’ valuations! While this may be reasonable to assume in a world where the auction is run repeatedly (among the same set of players), it would be difficult to believe that this equilibrium could occur in a single-shot auction. Instead, it seems more likely that players would “shade” their bids (i.e., underbid) based on their beliefs about the other players’ valuations. (Formalizing this requires assumptions about the distributions of players’ valuations; we briefly discuss this setting in the notes at the end of the chapter.)

In contrast, if we have a DST mechanism, everyone knows hows to bid, independent of their beliefs about the other players valuations (and strategies); indeed, this is why DST implementations are so desirable.

10.3 The VCG Mechanism

A natural question following the above discussion is whether we can find a mechanism that implements social value maximization in any context (and not just for single-good auctions). In fact, the Vickrey–Clarke–Groves (VCG) mechanism shows that this is possible; in particular, as we shall later see, we can use this mechanism to design an auction mechanism for matching markets.

Theorem 10.3. For every context $Γ$ , there exists a mechanism $ℳ$ that DST-implements social value maximization for $Γ$ .

Proof. Given a context $Γ = (n, Ω, T, \vec{v})$ , the mechanism $ℳ (\vec{r})$ —which we refer to as the plain VCG mechanism—outputs an outcome $(ω^{*}, \vec{p})$ such that:

$ω^{*} = arg max_{ω \in Ω} S V^{Γ} (\vec{r}, ω)$ (i.e., let $ω^{*}$ be the state that maximizes social value, $S V^{Γ} (\vec{r}, \cdot)$ , given reports $\vec{r}$ );

p_{i} = - \sum_{j \neq i} v_{j} (r_{j}, ω^{*})

. (That is, player

i

gets paid the total value the outcome generates to the remaining players

- i

assuming they actually have types

r_{- i}

If every player truthfully reports their type, then by the definition of $ω^{*}$ , this mechanism will select an outcome that maximizes social value. Let us now argue that $ℳ$ is DST. Consider some player $i$ with type $t_{i}$ ; assume the other players submit $r_{- i}$ . Then, if the mechanism selects the outcome $(ω^{*}, \vec{p})$ , player $i$ obtains utility

v_{i} (t_{i}, ω^{*}) - p_{i} = v_{i} (t_{i}, ω^{*}) + \sum_{j \neq i} v_{j} (r_{j}, ω^{*}) = S V^{Γ} ((t_{i}, r_{- i}), ω^{*}) .

So, player $i$ should submit a report $r_{i}$ such that $ℳ$ chooses $ω^{*}$ to maximize this expression. But, by submitting $t_{i}$ , $ℳ$ will, by construction, pick such a state. Thus, $t_{i}$ is a dominant strategy for player $i$ ; hence, $ℳ$ is DST and DST-implements social value maximization.

■

Note that if all players truthfully report their types, then all players get exactly the same utility, namely $S V^{Γ} (\vec{t}, ω^{*})$ , where $ω^{*}$ is the state selected by the mechanism $ℳ$ .

Computational efficiency of the plain VCG mechanism Note that if we can efficiently find the socially optimal outcome, then the plain VCG mechanism becomes computationally efficient.

The Clarke pivot rule: paying your “externality” In the plain VCG mechanism described above, the operator has to pay the players, which often is not desirable. We can modify the mechanism so that the players instead need to pay the operator. Specifically, if we shift the price of player $i$ in a manner that is independent of $i$ ’s report, the resulting mechanism will remain DST, since the price adjustment does not affect $i$ ’s preference between actions; that is, we now let

p_{i} = V_{i} (r_{- i}) - \sum_{j \neq i} v_{j} (r_{j}, ω^{*})

for any function $V_{i} (\cdot)$ . We refer to any such mechanism (obtained by shifting the prices in the plain VCG mechanism by $V_{i}$ ) as a VCG mechanism. A particularly useful instance—referred to as the Clarke pivot rule—is specified by letting

V_{i} (r_{- i}) = max_{ω \in Ω} \sum_{j \neq i} v_{j} (r_{j}, ω) .

That is, we are adjusting the prices by the “maximum social value if we were to exclude player $i$ from the game.” (As such, just as for the “plain VCG mechanism,” the VCG mechanism with the Clarke pivot rule is computationally efficient if we can efficiently find outcomes maximizing social value.)

Thus, player $i$ now needs to pay:

p_{i} = max_{ω \in Ω} \sum_{j \neq i} v_{j} (r_{j}, ω) - \sum_{j \neq i} v_{j} (r_{j}, ω^{*}) .

Note that this is always a non-negative amount, since the social value excluding $i$ at the state $ω^{*}$ can clearly never be higher than the maximum social value excluding $i$ .

A natural interpretation of the VCG mechanism with the Clarke pivot rule is that each player $i$ pays for the “harm” in value they cause the other players by being present in the game; this is called the player’s externality. With $i$ present, the other players get a total of $\sum_{j \neq i} v_{j} (r_{j}, ω^{*})$ ; without $i$ present, they would get $max_{ω \in Ω} \sum_{j \neq i} v_{j} (r_{j}, ω)$ . In other words,

p_{i} = max_{ω} S V_{- i} (\vec{r}, ω) - S V_{- i} (\vec{r}, ω^{*}),

where $S V_{- i} (\vec{r}, ω)$ denotes the social value of all players except $i$ , assuming that the player types are $\vec{r}$ , and where $ω^{*}$ is the outcome that maximizes social welfare for everyone including $i$ (given the player types $\vec{r}$ ).

Let us look at two brief examples of a VCG mechanism.

Example: Airport or train station A small town needs to decide whether to build an airport or a train station; let $Ω = {A, T}$ ( $A$ corresponds to building the airport and $T$ to building the train station.) For every inhabitant of the town (i.e., each player) $i$ , let the type space $T_{i}$ be a finite set of functions from $Ω$ to $ℕ$ , representing the monetary value they have for each outcome, and let the valuation function for each player $i$ be $v_{i} (t_{i}, ω) = t_{i} (ω)$ .

For instance, consider a situation where we only have 2 players, and let $t_{1} (A) = 10, t_{1} (T) = 0$ (i.e., player 1 strongly needs an airport and but has no need for a train station), and let $t_{2} (A) = 4$ , $t_{2} (T) = 6$ (i.e., player 2 weakly prefers a train station). Consider applying the VCG mechanism with the Clarke pivot rule to this context, assuming the players have types $t_{1}, t_{2}$ , and they truthfully report their types to the mechanism (as proven above, doing so is a dominant strategy). Clearly, the outcome $ω^{*}$ , which maximizes social value, is $A$ (with a social value of $10 + 4 = 14$ as opposed to $0 + 6 = 6$ for the outcome $T$ ); thus, the VCG mechanism will pick this outcome assuming players truthfully report their types.

Now, consider the externality of each player. Without player 1 present, $T$ would be the best outcome, and player 2 would receive 6 in utility. However, in the outcome $ω^{*}$ , player 2 receives only 4; thus, player 1’s externality is 2. Player 2’s externality is 0, since the outcome is the same regardless of whether player 2 is present or not. Thus, player 1 would be charged a price of 2, whereas player 2 would not be charged anything.

Example: Single-item auctions (recovering the second-price auction) Consider applying the VCG mechanism with the Clarke pivot rule for single-item auction contexts. Clearly, the item will be assigned to the player $i^{*}$ with the highest bid (as this maximizes social value).

The externality of player $i^{*}$ is equal to the second-highest bid: if $i^{*}$ were not present, the second-highest bidder $i^{* *}$ would win and receive value equal to their bid, but if $i^{*}$ is present, $i^{* *}$ gets nothing in value. None of the other players’ value is affected by $i^{*}$ showing up or not (they still do not get it), so the externality of player $i^{*}$ is exactly the second-highest bid. (Note that it is important that we consider the value and not utility for players when computing the externality!)

No other players have externalities, since their presence or absence does not affect the outcome ( $i^{*}$ will win either way). So they pay nothing. Hence, the VCG mechanism with the Clarke pivot rule gives us exactly a second-price auction when applied to single-item auction contexts!

10.4 VCG and Matching Markets

Let us now apply the VCG mechanism to the problem of designing a matching market auction. Recall that a matching market $(n, Y, \vec{v})$ specifies a set $[n]$ of players, a set $Y$ of objects, and for each player $i$ , a valuation function $v_{i} : Y \to ℕ$ . To view this as a mechanism design problem, we define a matching market context $(n, Ω, T, \vec{v})$ as follows:

$Ω$ (the set of states) is the set of all possible matchings $M$ in the complete bipartite graph over $[n] \cup Y$ (i.e., all possible allocations of items to players);
for each $i$ , $T_{i}$ is the set of all possible valuation functions $t_{i} : Y \to ℕ$ ;
$v_{i} (t_{i}, M) = t_{i} (M (i))$ if $M (i) \neq ⊥$ and 0 otherwise.

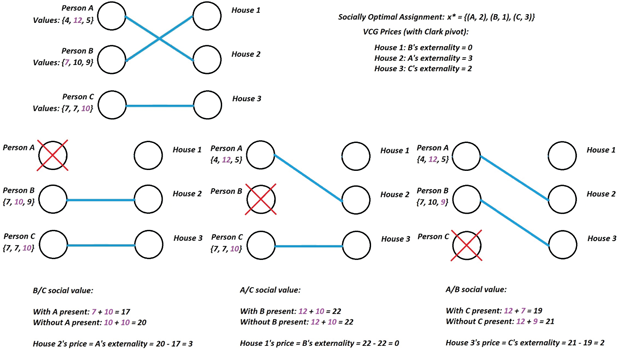
**Figure 10.2:** An illustration of VCG pricing using the Clarke pivot rule. The price each player pays is their externality, or the amount by which their presence in the auction decreases the other players’ social value. Notice that the Clarke VCG price for a player is equal to the standard VCG price plus the other players’ social value with that player absent.

We can now directly use VCG mechanisms on the social-choice context to get a matching market auction that DST-implements social value maximization (and hence social welfare maximization). See Figures 10.1 and 10.2 for an illustration of both the plain VCG and VCG with the Clarke pivot rule in the context of matching markets. For concreteness, the VCG mechanism with the Clarke pivot rule proceeds as follows:

Pick the allocation $M^{*}$ that maximizes $\sum_{i \in [n]} r_{i} (M^{*} (i))$ .
Set prices $p_{i} = max_{M \in Ω} \sum_{j \neq i} r_{j} (M (j)) - \sum_{j \neq i} r_{j} (M^{*} (j))$ (i.e., $p_{i}$ is $i$ ’s externality).

Computational efficiency Notice that to efficiently implement this mechanism, we need a way to efficiently find the matching (i.e., allocation) $M^{*}$ that maximizes social value. If we think of $v_{i} (t_{i}, y)$ as the weight of the edge $(i, y)$ in the bipartite graph over $[n] \times Y$ , this amounts to finding the maximum-weight bipartite matching of this graph. There are various direct ways of doing this; here, we simply remark that a combination of the market-clearing theorems we have already demonstrated shows how to efficiently find a matching $M^{*}$ that maximizes social value: Theorem 8.2 gives us a polynomial-time algorithm for finding a market equilibrium $(M^{*}, p)$ , which by Theorem 8.1 maximizes social welfare, and thus by Corollary 8.1, $M^{*}$ also maximizes also social value.

Revisiting bundles of identical goods Let us return to the case where we have a matching market in which the items are bundles of identical goods; recall that bundle $i$ contains $c_{i}$ goods, and we assume without loss of generality that $c_{1} > c_{2} > \dots > c_{n}$ . We can again specify this as a mechanism design context $(n, Ω, T, \vec{v})$ :

$Ω$ (the set of states) is the set of all possible matchings $M$ in the complete bipartite graph over $[n] \cup Y$ ;
for each $i$ , $T_{i} = ℕ$ —that is, each player’s type is now simply an integer (their value per individual object);
$v_{i} (t_{i}, M) = c_{M (i)} t_{i}$ .

We will refer to such a context as a market-for-bundles context. Let us again consider the VCG mechanism with the Clarke pivot rule for this context. Then $ℳ (\vec{r})$ proceeds as follows:

Pick an allocation

M^{*}

that maximizes social value (i.e.,

\sum_{i \in [n]} c_{M^{*} (i)} r_{j}

) as follow: Let

k (i)

be the

i^{th}

ranked player—that is, the player with the

i^{th}

highest bid, breaking ties lexicographically—and let

M^{*}

assign the

i^{th}

bundle to player

k (i)

Then, we need to charge the $i^{th}$ ranked player, $k (i)$ , its externality. Assuming truthful reporting, the optimal allocation for players ranked $j$ such that $j < i$ does not change if we remove player $k (i)$ , so it suffices to consider the change in value for players ranked $j > i$ . If player $k (i)$ is present, these players receive total value $\sum_{j > i} c_{j} r_{k (j)} .$
But if player $i$ is absent, each of these players gets the next-larger bundle, for a total value of
$\sum_{j > i} c_{j - 1} r_{k (j)} .$
So, the $i^{th}$ ranked player’s externality (and thus the price charged to them) is the difference between these values:
$p_{k (i)} = \sum_{j > i} (c_{j - 1} - c_{j}) r_{k (j)} .$

Note that a seemingly curious property of this auction is that the last ranked player gets the smallest bundle for free. This seems unrealistic. It turns out that this is not a real issue: If the seller also has some value for the items, as already discussed in chapter 8, we could add an “extra buyer” representing the seller’s interests (i.e., the extra buyer’s value would be the seller’s value for an item). If the seller’s value is the lowest one, this values will serve as a reserve price, and the lowest ranked “actual” buyer will always have to pay at least this reserve price.

10.5 Generalized Second-price (GSP) Auctions

While the VCG pricing for matching markets for bundles is relatively simple to compute, the mechanism is still a lot more complicated than the “simple” first- and second-price auctions for the case of single-item auction. As we have seen, in the case of a single-item auction, VCG (with the Clarke pivot rule) actually reduces down to a second-price auction. A natural question is whether we can get a similarly simple mechanism also for multi-item auctions. We restrict our attention to markets for bundles context.

Consider, now, the following natural generalization of the second-price mechanism: assign the $i^{th}$ bundle to the $i^{th}$ ranked player, $k (i)$ , and let them pay the ${(i + 1)}^{st}$ ranked bid per item—that is,

p_{k (i)} = c_{i} r_{k (i + 1)}

if $i < n$ and $p_{k (n)} = 0$ . This mechanism, which was introduced by Google, is referred to as the generalized second-price (GSP) mechanism.

GSP is not DST Despite the fact that the GSP seems like a natural generalization of the second-price auction (which we know is DST for the case of single-item auctions), GSP is not DST when considering multiple bundles! To see this, consider the following example: let us say we have three bundles of items with $c_{1} = 10$ , $c_{2} = 4$ , $c_{3} = 0$ and three players with unit values $t_{1} = 7$ , $t_{2} = 6$ , $t_{3} = 1$ . If the players bid truthfully, player 1 gets the largest bundle ( $10$ ) for the second-highest price ( $6$ ), thus earning utility $7 (10) - 6 (10) = 10$ . But if player 1 were to deviate and report their valuation at $5$ , they would get the second-largest bundle ( $4$ ) at the third-highest price ( $1$ ), earning utility $7 (4) - 1 (4) = 24$ . So in this case, bidding truthfully is not a PNE!

GSP Nash-implements social value maximization However, despite the fact that GSP is not truthful, it is actually the mechanism that Google and other sellers of advertising slots use for sponsored search advertisements! Among other factors, this may be because the simplicity of the auction is appealing—bidders can easily understand how much they will have to pay. In addition, as we now show, GSP does Nash-implement social value maximization:

Theorem 10.4. The GSP mechanism Nash-implements social value maximization in any market-for-bundles context.

Proof. It suffices to show that there is some Nash equilibrium in the induced game that maximizes social value. Let us start by considering the case that player $k$ has the $k^{th}$ ranked valuation for the items being sold (i.e., the players are ordered according to their valuations).

By Theorem 8.2, there exists a market equilibrium in the matching market corresponding to this social choice context. By Theorem 8.1, this equilibrium maximizes social value, and so we can assume, without loss of generality, that in this equilibrium player $k$ is assigned bundle $k$ (since we ordered players by decreasing valuation and bundles by decreasing size; if a tie causes players to be assigned bundles out of order, we can reorder them accordingly while still maintaining the equilibrium property). Additionally, by the construction in Theorem 8.1, there exists some market equilibrium where the price of the cheapest bundle is 0.

Now, let $α_{i}$ be the price per item in bundle $i$ ; by Theorem 8.3, we have that $α_{1} \geq α_{2} \geq \dots \geq α_{n} = 0$ . Consider the bidding strategy where $r_{i} = α_{i - 1}$ if $i > 1$ and $r_{1} = α_{1} + 1$ . Since $r_{k} \geq r_{k + 1}$ for any $k$ , and because we have assumed ties to be broken lexicographically, the GSP mechanism will assign player $k$ to bundle $k$ , and so $\vec{r}$ maximizes social value by the above. It remains to show that $\vec{r}$ is a PNE.

Notice that, by construction of $\vec{r}$ , player $i$ will receive the same bundle as in the market equilibrium (i.e., bundle $i$ ) and at the market-clearing price $α_{i}$ . (Note that player $n$ receives it at price $0$ , which by construction of the market equilibrium, is equal to $α_{n}$ .)

Let us now argue that player $i$ has no incentives to deviate. Consider some deviation by player $i$ . If the deviation leads to the same assignment for $i$ , their utility remains the same, so the deviation is not profitable. Let us thus consider some deviation where $i$ gets assigned a different bundle $j$ . We distinguish two cases:

Overbidding: If player $i$ overbids so that they now gets assigned a bigger bundle $j < i$ , they “push down” player $j$ (to position $j + 1$ ) and will thus have to pay the bid $r_{j} \geq α_{j}$ of player $j$ per item.
Underbidding: If player $i$ underbids so that they now gets assigned a smaller bundle $j > i$ , they “push up” player $j$ (to position $j - 1$ ) and will thus have to pay the bid $r_{j + 1} = α_{j}$ of player $j + 1$ per item (just as player $j$ previously did).

Thus, in both cases, $i$ gets assigned a bundle $j$ and has to pay at least $α_{j}$ for it. By the market-clearing property of $\vec{α}$ , player $i$ cannot prefer getting bundle $j$ at price $α_{j}$ to getting its current bundle $i$ at price $α_{j}$ , so in neither case, the deviation can be profitable for $i$ . This concludes the proof that $\vec{r}$ is a PNE.

So far, however, we have only considered the case when the players are ordered according to their valuations. To deal with the general case, it suffices to note that the above argument applies unchanged if we replace “player $i$ ” with “the $i^{th}$ ranked player” (where ranking is defined in terms of players’ valuations).

■

10.6 Applications to Sponsored Search

An important real-life example of a matching market auction is the market for sponsored search. Here, a search engine (e.g., Google) sells advertising “slots” for search terms. For instance, when a user makes a search for “learn programming,” Google has four advertisements that appear before the actual search results; see Figure 10.3. To determine which ads to show, Google uses an auction for bundles of identical goods. The items being sold are “clicks” (i.e., instances of a user clicking on the ad), and the “size” of each of the bundles (slots) is the number of clicks an advertiser would expect to get from each of them—the clickthrough rate. (We are incorrectly assuming that clickthrough rates are the same no matter who the advertiser is; this will be discussed shortly.) Each advertisers $i$ ’s type, $t_{i}$ , is its value for a click.

In such a scenario, we can use either the VCG mechanism or the GSP mechanism to sell these advertising slots, and charge the buyers accordingly. Our previous analysis applies directly if we charge the advertiser for each search taking place—that is, we charge per impression of the ad—the (expected) value for advertiser $i$ for a slot $j$ with clickthrough rate $c_{j}$ is $c_{j} t_{i}$ , just as in a market-for-bundles context.

Charging per click Search engines typically no longer charge per impression of an ad, but instead charge by the click. The auctions can easily be modified to capture this setting by instead charging a user $i$ placed on slot $j$ $p_{i} / c_{j}$ per click; in the case of GSP, this simplifies the auction even further, as we can now simply charge the $i^{th}$ ranked user the ${(i + 1)}^{st}$ ranked bid!

Dealing with ad quality So far in this discussion, we have assumed that the clickthrough rate per slot is independent of the advertiser (or ad) being placed there. This is clearly unrealistic—a relevant ad, for instance, is far more likely to get more clicks than an irrelevant “spam” advertisement. To model this, we assume that each advertiser $i$ has a “quality” or discount parameter $q_{i}$ —an “optimal advertiser” has $q_{i} = 1$ , but a spammer may have a significantly lower value of $q_{i}$ —and an advertisement by player $i$ placed on slot $j$ is assumed to get $c_{j} q_{i}$ clicks. We can again model this as a market for bundles; each bundle of $c_{j}$ items is now a bundle of “fictitious clicks,” where each fictitious click leads to (in expectation) $q_{i}$ actual clicks to an advertiser $i$ . In other words, the (expected) value for player $i$ for a fictitious click is $t_{i} q_{i}$ (assuming that $q_{i}$ is correct).

The quality $q_{i}$ of an advertiser $i$ is estimated by the search engine, and we thus assume that mechanism is aware of it. If we assume the search engine’s estimates are actually correct, the following mechanism can be used in this setting:

As before, each player $i$ submits a bid $r_{i}$ for a click. (The bid is supposed to be their value for an “actual” click.)
The mechanism first computes a “discounted bid” $r_{i}^{'} = r_{i} q_{i}$ ; think of $r_{i}^{'}$ as player $i$ ’s value for a “fictitious click.”
We next run the VCG or GSP mechanisms for bundles assuming player $i$ ’s bid is $r_{i}^{'}$ to get an allocation-pricing pair $(M, \vec{p})$ .
Finally, let $p_{i}^{'} = \frac{p_{i}}{q_{i} c_{M (i)}}$
and output $(M, {\vec{p}}^{'})$ . (Recall that $p_{i}$ is the price for the impression; thus, $\frac{p_{i}}{c_{M (i)}}$ is the price per fictitious click, and $\frac{p_{i}}{q_{i} c_{M (i)}}$ becomes the price per actual click assuming the quality estimate is correct.)

Notes

The development of mechanism design theory began with the work of Hurwicz [Hur60]. The VCG mechanism was introduced and analyzed in the works of Vickrey [Vic61], Clarke [Cla71], and Groves [Gro73]. The generalized second-price auction was introduced and analyzed in [EOS07].

Let us also mention that the literature on mechanism design often also considers a setting, referred to as Bayesian, where players’ types come from a probability distribution $D$ (typically, we assume that player types are independent). In such a setting we may then consider a weaker notion of a “Bayes–Nash truthful” mechanism, where every player’s expected utility (where the expectation is over the distribution of other players’ types) is maximized by truthfully reporting their type; this is formalized by defining a generalized version of a normal-form game called a Bayesian Game, where players first receive a type sampled from $D$ and then need to choose their action (without knowing the actual type that was sampled for the other players.) The notion of a Bayes–Nash truthful implementation is no longer equivalent to DST; optimal Bayes–Nash truthful auctions were studied in work of Myerson [Mye81]. Leonid Hurwicz, Eric S. Maskin, and Roger B. Myerson received the Nobel Prize in Economic Sciences (for laying the foundation of mechanism design theory) in 2007.

As mentioned above, the VCG mechanism is computationally efficient as long as we have a computationally efficient method for finding socially optimal outcomes. For many optimization problems, however, it is computationally hard to find the socially optimal state (even if people truthfully report the preferences); consequently, the computer science literature has focused on studying so-called approximation algorithms, where we contend ourselves with finding a “close-to-optimal” outcome. Can we simply plug in such an approximation algorithm into the VCG mechanism? It turns out that the resulting mechanism no longer is DST. In fact (assuming the existence of “secure encryption schemes”), no computationally efficient “general-purpose” mechanisms (like VCG)—which simply use some underlying approximation algorithm as a “black-box”—can be DST [PS14, CIL12]. Consequently, the computer science literature has focused on directly designing DST mechanism that attempt that guarantee “close-to-optimal” outcomes: this study—referred to as algorithmic mechanism design—was initiated by Nisan and Ronen [NR99]. See [NRTV07] for a detailed study of this area.

¹It may seem redundant for players to be associated with both a type $t_{i}$ as well as an individualized valuation function $v_{i}$ (which depends on the player identity $i$ ). Indeed, formally, it suffices to consider a single valuation function $v$ and assume that the type $t_{i}^{'}$ contains information about who the player is (e.g., let $t_{i}^{'} = (i, t_{i})$ ), but this makes notation more cumbersome, and makes the notion of a type less intuitive.

²Let us point out that, while this way of defining utility is seemingly the most natural and simple way to capture the preferences of a player, there are some situations where the use of quasi-linear utilities are not appropriate—for instance, the fact that utility is linear in the payment $p_{i}$ does not capture the phenomena that people treat a price gap of $10 very differently depending whether they are buying, say, laundry detergent or a car. Nevertheless, in situations where the payments $p_{i}$ are “small” compared to the wealth of the players, this “quasi-linear” model seems reasonable.

³Note that we here are making use of the fact that $v_{i}$ is parametrized by the player identity $i$ to determine whether $i$ is actually receiving the object.