Component 1 - Final Report

Appendix A: Simulator

Goal

draw conclusions about network loss and delay characteristics

determine the suitability of a link for the transmission of audio data

determine the effectiveness of our proposed FEC algorithm in terms of the number of additional samples played

determine optimal values for the parameters to the adaptive playout and adaptive FEC algorithms. This includes (i) examining the relationship between the parameters and (ii) choosing values for the parameters in order to "save" as many delayed or lost packets as possible while keeping the buffering delay to a minimum.

Experimental Design

Our data were collected at five specific times in a day; these are:
Fri Nov 20 00:06:52 EST 1998
Fri Nov 20 05:07:01 EST 1998
Fri Nov 20 10:07:13 EST 1998
Fri Nov 20 15:07:17 EST 1998
Fri Nov 20 20:07:05 EST 1998

In particular, we used ping packets of the same size as the packets generated by our component software. These packets are transmitted by a modified version of the ping(1) program. From the trace files we obtain the sequence number and the round-trip time of every ping packet we receive.

Assumptions

Packets of fixed size are generated and sent at the sending host at fixed time intervals. Precisely, a packet of X bytes is sent every (X*1000000/11025) microseconds.

The transmission time is half of the round-trip time and packet loss rates are determined based on packet sequence numbers we obtain from the ping trace-files.

The clocks of the sending host and the receiving hosts are perfectly synchronized. As a consequence, the reception time of a packet is simply the sum of the send time and the transmission delay of the packet. (With modern hardware it is reasonable to assume that the clocks of the sending and receiving hosts differ by a constant over time, i.e., clock drifts are negligible. Hence without this assumption we only need to add a constant factor when we calculate the reception time of a packet. As we shall see, the absence of this constant factor will not affect our determination of optimal values for the parameters.)

Links are lossy, so packets may be lost.

The receiving host has infinite buffering capacity. (At the very least its capacity is large enough to hold all the out-of-order packets.)

Special features of the simulator

Talkspurt generation

A source's audio is typically divided into "talkspurts" (periods of audio activity) and "silence periods" (periods of audio inactivity, during which no audio packets are generated). In order to faithfully reconstruct the audio at the receiving host, data in packets within a talkspurt must be played out in the same periodic manner in which they are generated. In order to model the existence of talkspurts in audio, we artificially divide our ping packets into talkspurts using a function that has an exponential distribution with a mean of 1.6. This function is widely accepted to be an accurate model of talkspurts in human speech.

Talkspurt-based adaptive playout

The principal reason for buffering received audio packets (delaying their playouts) is to provide synchronous playout of audio packets in the face of stochastic end-to-end network delays. That is, we hope that by buffering received packets for enough time most of them will have been received before their scheduled playout times. This additional artificial delay until playout can either be fixed throughout the duration of an audio call, or may vary adaptively during a call lifetime. Previous research confirms that adaptive playout algorithms outperform their non-adaptive counterparts; hence we choose to implement one of the adaptive playout algorithms proposed in [5].

Before presenting the algorithm, we first give an intuitive idea of how to choose the optimal delay. We are primarily concerned with two sources of delay: transmission delay and buffering delay. Let p_hat be the sum of transmission delay and buffering delay. Clearly, for each packet,

playout time = p_hat + send time

Now, suppose we know the send time and reception time of every audio packet in a call in advance. Then a reasonable value for p_hat is the maximum of the difference between the reception time and send time over all packets, since every packet will have been received by its scheduled playtime given this choice of p_hat. There are two ceveats: (1) We do not know the reception time of a packet in advance and (2) We want to make p_hat as small as possible, since excessively long playout delays can significantly impair human conversations. So the goal of adaptive playout is to choose p_hat based on past performance.

The following is a sketch of the algorithm for choosing p_hat. Note that p_hat is changed once per talkspurt (hence the name talkspurt-based adaptive playout). Let

SAFETY_FACTOR = minimum packet buffering delay enabling us to combine adaptive playout and adaptive FEC by specifying a "smallest time" that packets will be buffered before playout
n = transmission delay + SAFETY_FACTOR
d = the exponential average of the n's
v = the exponential average of the variance(d)Æs
Alpha = 0.998002
Beta = 4 (variation coeffient that provides slack in playout delay for arriving packets)

in NORMAL mode:
d = (1.0-Alpha) * n + Alpha * d;

in SPIKE mode:
d = d + (n of current packet) û (n of previous packet);

v = (1.0-Alpha) * abs(n û d) + Alpha * v;

if (we reach the start of a talkspurt) then
p_hat = d + Beta * v;

Exact simulation of the ring buffer from the point of view of an application

In our component software every audio packet is stored in a data structure called a ring buffer upon receipt. Needless to say, this data structure must permit timely location (and hence delivery) of any packets stored in it. With a complementary indexing structure into the ring buffer, which is implemented as a circular array, we are able to retrieve each packet stored in the ring buffer in asymptotic constant time. From an application standpoint, all it is concerned about is whether it can get an audio packet by the time it needs to be played out. Besides providing the abstraction that packets arrive in order, the ring buffer satisfies the needs of an application by determining whether a packet arrives before its scheduled play time and substituting a delayed packet for the corresponding FEC packet automatically if the FEC packet is in the ring buffer. In essence, the simulator provides the same functionality as the ring buffer by classifying each packet p sent by the sending host as belonging to one of the following three groups:

p arrives on time, meaning that it can be played out normally
p does not arrive on time, but the corresponding FEC packet p has been received by the time p needs to be played out and hence can be used to substitute p
p does not arrive on time, and the corresponding FEC packet p has not been received by the time p needs to be played out.

Adaptive FEC

The simulator provides the option of adaptively changing fec_delta per talkspurt, where fec_delta is defined to be the difference between the sequence numbers of the two packets carrying the same audio data. Our experiments show that, with the same buffering delay, changing fec_delta adaptively enables us to save more delayed/lost packets. The determination of the optimal fec_delta at a given point in time is based on Wes's Contention Theorem, which describes a receiver-side method for calculating the highest usable fec_delta for the receiver on a per-source basis.

Wes's Contention Theorem:

The highest usable fec_delta is the minimum of w1, w2 and w3, where
w1 = the maximum number of packets lost/delayed consecutively
w2 = the maximum number of packets consecutively received in time for playout
w3 = the quotient of the current buffering delay and the sender-side sampling interval

Proof. For 3), we estimate the buffering delay as follows:
By definition,
scheduled play time = send time + p_hat. (i)
p_hat = d + Beta * v (ii)
reception time = send time + transmission delay (iii)
n = transmission delay + SAFETY_FACTOR (iv)

So, buffering delay
= scheduled play time û reception time (def of buffing delay)
= send time + p_hat û reception time (by (i))
= send time + d + Beta * v û reception time (by (ii))
= d + Beta * v û transmission delay (by (iii))
= SAFETY_FACTOR + Beta * v (assume d ~ n and by (iv))

The transmission delay pattern of packets can be captured by the following graph.

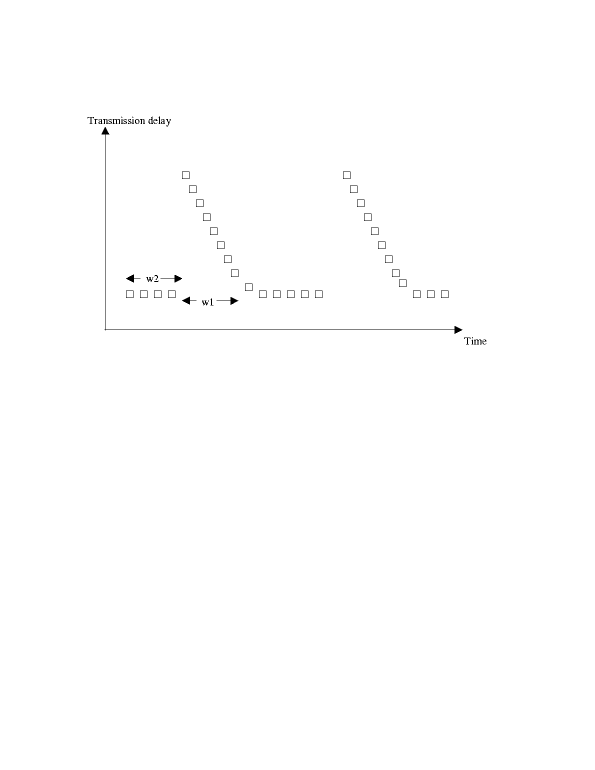
In general, a sequence of packets arriving at the receiving host before the scheduled playout time is followed by a burst of delayed packets, and the same pattern repeats over time. If w1 > w2, then w2 out of the w1 delayed packets can be saved by FEC in the best case. This is achieved by setting fec_delta to be w2. If w2 > w1, then it is possible for us to save all the w1 delayed packets by setting fec_delta to be w1. This implies fec_delta = min(w1, w2). Now, note that w3 is an upper bound on fec_delta, since for any packet p with sequence number x, packets with sequence number greater than x + w3 will not have been received before the scheduled playout time of p and hence cannot be used as FEC packets of p. Hence, the optimal fec_delta is min(w1, w2, w3). (Q.E.D.)