Factorization Method
Our algorithm to recover the 3D shape of the target object is based on the Factorization method proposed by Tomasi and Kanade[Tomasi and Kanade, 1992]. This method attempts to recover both the 3D shape of a target object and the motion of the camera from a sequence of images under orthographic projection. The input to the factorization method is a measurement matrix W, representing image positions of tracked feature points over the image frames.
If we have tracked P feature points over F frames, then let U be a FxP matrix such that each column of U contains all the observations for a single point, while each row of the first F rows contains all the observed x-coordinates; similarly, let V be a FxP containing the observed y-coordinates. We will call the combined matrix of U and V the measurement matrix W of size 2FxP.
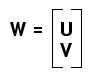
Under orthography, W is theoretically the product of the 2Fx3 camera motion matrix M and the 3xP shape matrix S. M is composed of orthonormal vectors if and jf, which correspond to the x-axis and y-axis of each image plane f. S is the collection of 3D coordinates sp of each feature point in a fixed world coordinate system. Notice that W is at most rank 3.
The procedure of the factorization method consists of two steps. First, decompose W into two matrices M' and S' using Singular Value Decomposition. The product of M'xS' is the best possible rank three approximation to W. However, this decomposition is not unique, because there can exist any 3x3 non-singular matrix Q such that
W = M'S' = (M'Q)(Q-1S') = M''S''
The second step of the method is to find the right Q which transforms M' and S' to the true solutions M and S. Observing that the rows if and jf of M must satisfy the normalization and orthogonality constraints, we can obtain the system of 3xF overdetermined equations such that
ifT QTQ if = 1
jfT QTQ jf = 1
ifT QTQ jf = 0
This involves solving a quadratic matrix system which is non-trivial. Instead, we solve for the symmetric matrix L = QTQ using some data fitting techniques. The real solution for L has been proved by ourselves to be positive definite; therefore, we can take the cholesky factorization of the approximated solution assuming that it will be closely positive definite to get Q.