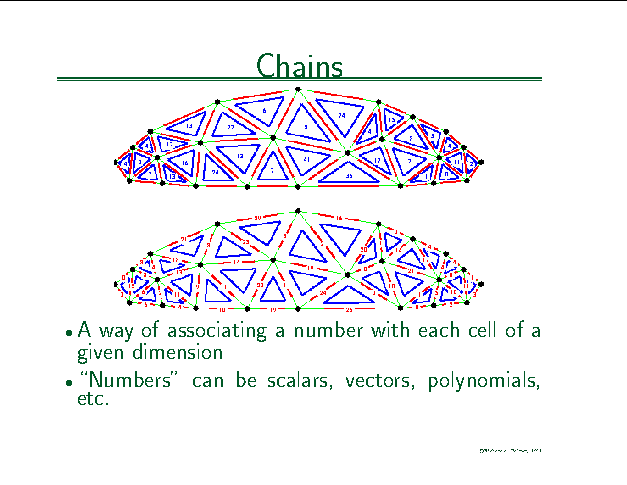
Where cells and cell complexes provide the mathematical machinery for decomposing space into simple regions, with sufficient structure to represent the relationships between these regions, chains are used to associate physical quantities with these regions. For computer representations, we use finite chains, i.e., chains defined over finite cell complexes.
This slide illustrates a pair of chains whose coefficients are integers. The top illustration denotes a 2-chain. The number displayed at the center of each 2-cell represents the coefficient of that cell. AAn an example, aa 2-chain could be used to represent the mass or area contained in aa 2-cell. Similarly, the bottom illustration denotes a 1-chain. The number displayed at the center of each 1-cell represents the coefficient of that cell in the chain.
There is an important relationship between the notion of a chain and that of a measurement: associated with each measurement is a dimension. For instance, displacement is measured at a point, while distance is measured along a path, and flux is measured through a surface. For this reason, a 0-chain is used to represent displacement, a 1-chain for distance, and a 2-chain for flux (in a three dimensional region).