![[image]](images/fig1-1.jpg)
Actual Causality
The MIT Press
Cambridge, Massachusetts
London, England
© 2016 Massachusetts Institute of Technology
All rights reserved. No part of this book may be reproduced in any form by any electronic or mechanical means (including photocopying, recording, or information storage and retrieval) without permission in writing from the publisher.
This book was set in LATEX by Joseph Y. Halpern. Printed and bound in the United States of America.
Library of Congress Cataloging-in-Publication Data
Names: Halpern, Joseph Y., 1953
Title: Actual causality / Joseph Y. Halpern.
Description: Cambridge, MA : The MIT Press, [2016] — Includes bibliographical references and index.
Identifiers: LCCN 2016007205 — ISBN 9780262035026 (hardcover : alk. paper)
Subjects: LCSH: Functional analysis. — Probabilities. — Causation.
Classification: LCC QA320 .H325 2016 — DDC 122dc23 LC record available at http://lccn.loc.gov/2016007205
10987654321
For David, Sara, and Daniel (yet again). It’s hard to believe that you’re all old enough now to read and understand what I write (although I’m not sure you will want to!). The theory of causality presented here allows there to be more than one cause, and for blame to be shared. You’re all causes of my happiness (and have, at various times, been causes of other states of mind). I’m happy to share some blame with Mom for how you turned out.
Contents
2The HP Definition of Causality
2.2A Formal Definition of Actual Cause
2.2.1A language for describing causality
2.2.2The HP definition of actual causality
2.7Causality in Nonrecursive Models
2.10.2Proof of Proposition 2.4.6
2.10.3Proof of Proposition 2.9.2
3Graded Causation and Normality
3.1Defaults, Typicality, and Normality
3.4.5Legal doctrines of intervening causes
3.5An Alternative Approach to Incorporating Normality
4.1Adding Variables to Structure a Causal Scenario
4.3Using the Original HP Definition Instead of the Updated Definition
4.4The Stability of (Non-)Causality
4.6Dependence and Independence
4.7Dealing With Normality and Typicality
4.8.3Proofs and example for Section 4.4
5Complexity and Axiomatization
5.1Compact Representations of Structural Equations
5.2Compact Representations of the Normality Ordering
5.2.1Algebraic plausibility measures: the big picture
5.2.2Piggy-backing on the causal model
5.3The Complexity of Determining Causality
5.4Axiomatizing Causal Reasoning
5.5Technical Details and Proofs
5.5.1Algebraic plausibility measures: the details
5.5.2Proof of Theorems 5.3.1 (c) and 5.3.2 (b)
5.5.3Proof of Theorems 5.4.1, 5.4.2, and 5.4.4
6.1A Naive Definition of Responsibility
6.3Responsibility, Normality, and Blame
7.1Explanation: The Basic Definition
7.2Partial Explanations and Explanatory Power
7.3The General Definition of Explanation
In The Graduate, Benjamin Braddock (Dustin Hoffman) is told that the future can be summed up in one word: “Plastics”. I still recall that in roughly 1990, Judea Pearl told me (and anyone else who would listen!) that the future was in causality. I credit Judea with inspiring my interest in causality. We ended up writing a paper on actual causality that forms the basis of this book. I was fortunate to have other coauthors who helped me on my (still ongoing) journey to a deeper understanding of causality and related notions, particularly Hana Chockler, Chris Hitchcock, and Tobi Gerstenberg. Our joint work features prominently in this book as well.
I thank Sander Beckers for extended email discussions on causality, Robert Maxton for his careful proofreading, and Chris Hitchcock, David Lagnado, Jonathan Livengood, Robert Maxton, and Laurie Paul for their terrific comments on earlier drafts of the book. Of course, I am completely responsible for any errors that remain.
My work on causality has been funded in part by the NSF, AFOSR, and ARO; an NSF grant for work on Causal Databases was particularly helpful.
Introduction and Overview
Felix qui potuit rerum cognoscere causas. (Happy is one who could understand the causes of things.)
Virgil, Georgics ii.490
Causality plays a central role in the way people structure the world. People constantly seek causal explanations for their observations. Why is my friend depressed? Why won’t that file display properly on my computer? Why are the bees suddenly dying?
Philosophers have typically distinguished two notions of causality, which they have called type causality (sometimes called general causality) and actual causality (sometimes called token causality or specific causality; I use the term “actual causality” throughout the book). Type causality is perhaps what scientists are most concerned with. These are general statements, such as “smoking causes lung cancer” and “printing money causes inflation”. By way of contrast, actual causality focuses on particular events: “the fact that David smoked like a chimney for 30 years caused him to get cancer last year”; “the fact that an asteroid struck the Yucatan Peninsula roughly 66 million years ago caused the extinction of the dinosaurs”; “the car’s faulty brakes caused the accident (not the pouring rain or the driver’s drunkenness)”.
The reason that scientists are interested in type causality is that a statement of type causality allows them to make predictions: “if you smoke a lot, you will get (or, perhaps better, are likely to get) lung cancer”; “if a government prints $1 billion, they are likely to see 3% inflation”. Because actual causality talks about specific instances, it is less useful for making predictions, although it still may be useful in understanding how we can prevent outcomes similar to that specific instance in the future. We may be interested in knowing that Robert’s sleeping in caused him to miss the appointment, because it suggests that getting him a good alarm clock would be useful.
Actual causality is also a critical component of blame and responsibility assignment. That is perhaps why it arises so frequently in the law. In the law, we often know the relevant facts but still need to determine causality. David really did smoke and he really did die of lung cancer; the question is whether David’s smoking was the cause of him dying of lung cancer. Similarly, the car had faulty brakes, it was pouring rain, and the driver was drunk. Were the faulty brakes the cause of the accident? Or was it the rain or the driver’s drunkenness? Of course, as the dinosaur-extinction example shows, questions of actual causality can also be of great interest to scientists. And issues of type causality are clearly relevant in the law as well. A jury is hardly likely to award large damages to David’s wife if they do not believe that smoking causes cancer.
As these examples show, type causality is typically forward-looking and used for prediction. Actual causality, in contrast, is more often backward-looking. With actual causality, we know the outcome (David died of lung cancer; there was a car accident), and we retrospectively ask why it occurred. Type causality and actual causality are both of great interest and are clearly intertwined; however, as its title suggests, in this book, I focus almost exclusively on actual causality and notions related to it.
Most of the book focuses on how to define these notions. What does it mean to say that the faulty brakes were the cause of the accident and not the driver’s drunkenness? What does it mean to say that one voter is more responsible than another for the outcome of an election? Defining causality is surprisingly difficult; there have been many attempts to do so, going back to Aristotle. The goal is to get a definition that matches our natural language usage of the word “causality” (and related words such as “responsibility” and “blame”) and is also useful, so that it can be used, for example, to provide guidance to a jury when deciding a legal case, to help a computer scientist decide which line in a program is the cause of the program crashing, and to help an economist in determining whether instituting an austerity program caused a depression a year later.
The modern view of causality arguably dates back to Hume. (For the exact citation, see the notes at the end of this chapter.) Hume wrote:
We may define a cause to be an object followed by another, and where all the objects, similar to the first, are followed by objects similar to the second. Or, in other words, where, if the first object had not been, the second never had existed.
Although Hume says “in other words”, he seems to be conflating two quite different notions of causality here. The first has been called the regularity definition. According to this definition, we can discern causality by considering just what actually happens, specifically, which events precede others. Roughly speaking, A causes B if As typically precede Bs. (Note that this is type causality.)
By way of contrast, the second notion involves counterfactuals, statements counter to fact. It does not consider just what actually happened but also what might have happened, had things been different. Research in psychology has shown that such counterfactual thinking plays a key role in determining causality. People really do consider “what might have been” as well as “what was”.
A recent experiment illustrates this nicely. Compare Figures 1.1(a) and (b). In both, ball A is heading toward a goal. In Figure 1.1(a), its path is blocked by a brick; in Figure 1.1(b), it is not blocked. Now ball B hits A. As a result, instead of going straight toward the goal, A banks off the wall and goes into the goal. In both figures, the same thing happens: B hits A, then A banks off the wall and goes into the goal. But when people are asked whether B hitting A caused A to go into the goal, they typically answer “yes” for Figure 1.1(a) and “no” for Figure 1.1(b). Thus, they are clearly taking the counterfactual (what would have happened had A not hit B) into account when they answer the question.
![[image]](images/fig1-1.jpg)
Figure 1.1: Considering counterfactuals.
There have been many definitions of causality that involve counterfactuals. In this book, I consider only one of them (although it comes in three variants), which Judea Pearl and I developed; this has been called the Halpern-Pearl definition; I call it simply the “HP definition” throughout this book. I focus on this definition partly because it is the one that I like best and am most familiar with. But it has a further advantage that is quite relevant to the purposes of this book: it has been extended to deal with notions such as responsibility, blame, and explanation. That said, many of the points that I make for the HP definition can be extended to other approaches to causality involving counterfactuals.
Pretty much all approaches involving counterfactuals take as their starting point what has been called in the law the “but-for” test. A is a cause of B if, but for A, B would not have happened. Put another way, this says that the occurrence of A is necessary for the occurrence of B. Had A not occurred, B would not have occurred. When we say that A caused B, we invariably require (among other things) that A and B both occurred, so when we contemplate A not happening, we are considering a counterfactual. This kind of counterfactual reasoning clearly applies in the example above. In Figure 1.1(a), had A not hit B, B would not have landed in the goal, so A hitting B is viewed as a cause of B going in the goal. In contrast, in Figure 1.1(b), B would have gone in the goal even if it had not been hit by A, so A hitting B is not viewed as a cause of B going in the goal.
But the but-for test is not always enough to determine causality. Consider the following story, to which I will return frequently:
Suzy and Billy both pick up rocks and throw them at a bottle. Suzy’s rock gets there first, shattering the bottle. Because both throws are perfectly accurate, Billy’s would have shattered the bottle had it not been preempted by Suzy’s throw.
Here the but-for test fails. Even if Suzy hadn’t thrown, the bottle would have shattered. Nevertheless, we want to call Suzy’s throw a cause of the bottle shattering and do not want to call Billy’s throw a cause.
The HP definition deals with this problem by allowing the but-for test to be applied under certain contingencies. In the case of Suzy and Billy, we consider the contingency where Billy does not throw a rock. Clearly, if Billy does not throw, then had Suzy not thrown, the bottle would not have shattered.
There is an obvious problem with this solution: we can also consider the contingency where Suzy does not throw. Then the but-for definition would say that Billy’s throw is also a cause of the bottle shattering. But this is certainly not what most people would say. After all, it was Suzy’s rock that hit the bottle (duh … ). To capture the “duh” reaction, the definition of causality needs another clause. Roughly speaking, it says that, under the appropriate contingencies, Suzy’s throw is sufficient for the bottle to shatter. By requiring sufficiency to hold under an appropriate set of contingencies, which takes into account what actually happened (in particular, that Billy’s rock didn’t hit the bottle), we can declare Suzy’s throw to be a cause but not Billy’s throw. Making this precise in a way that does not fall prey to numerous counterexamples is surprisingly difficult.
I conclude this introduction with a brief overview of the rest of the book. In the next chapter, I carefully formalize the HP definition. Doing so requires me to introduce the notion of structural equations. The definition involves a number of technical details; I try to introduce them as gently as possible. I then show how the definition handles the rock-throwing example and a number of other subtle examples that have come up in the philosophy and law literatures. I also show how it deals with issues of transitivity, and how it can be extended to deal with situations where we have probabilities on outcomes.
There are several examples that the basic HP definition does not handle well. It is well known in the psychology literature that when people evaluate causality, they take into account considerations of normality and typicality. As Kahneman and Miller have pointed out, “[in determining causality], an event is more likely to be undone by altering exceptional than routine aspects of the causal chain that led to it”. In Chapter 3, I present an extension of the basic HP definition that takes normality into account and show that the extension deals with some of the problematic cases mentioned in Chapter 2.
The HP definition of causality is model-relative. A can be a cause of B in one model but not in another. As a result, two opposing lawyers can disagree about whether A is a cause of B even if they are both working with the HP definition; they are simply using different models. This suggests that it is important to have techniques for distinguishing whether one model is more appropriate than another. More generally, we need techniques for deciding what makes a model “good”. These issues are the focus of Chapter 4.
For an approach to causality to be psychologically plausible, humans need to be able to represent causal information in a reasonably compact way. For an approach to be computationally feasible, the questions asked must be computable in some reasonable time. Issues of compact representations and computational questions are discussed in Chapter 5. In addition, I discuss an axiomatization of the language of causality.
Causality is an all-or-nothing concept; either A is a cause of B or it is not. The HP definition would declare each voter in an 11–0 vote a cause of the outcome; it would also call each of the six people who voted in favor of the outcome a cause in a 6–5 victory. But people tend to view the degree of responsibility as being much lower in the first case than the second. In Chapter 6, I show how the HP definition can be extended to provide notions of responsibility and blame that arguably capture our intuitions in these cases.
Causality and explanation are clearly closely related. If A is a cause of B, then we think of A as providing an explanation as to why B happened. In Chapter 7, I extend the structural-model approach to causality to provide a definition of explanation.
I conclude in Chapter 8 with some discussion of where we stand and some examples of applications of causality.
I have tried to write this book in as modular a fashion as possible. In particular, all the chapters following Chapter 2 can be read independently of each other, in any order, except that Sections 4.4, 4.7, 5.2, and 6.3 depend on Section 3.2. Even in Chapter 2, the only material that is really critical in later chapters is Sections 2.1–2.3. I have tried to make the main text in each chapter as readable as possible. Thus, I have deferred technical proofs to a final section in each chapter (which can be skipped without loss of continuity) and have avoided in some cases a careful discussion of the many viewpoints on some of the more subtle issues. There are a few proofs in the main text; these are ones that I would encourage even non-mathematical readers to try reading, just to get comfortable with the notation and concepts. However, they can also be skipped with no loss of continuity.
Each chapter ends with a section of notes, which provides references to material discussed in the chapter, pointers to where more detailed discussions of the issues can be found, and, occasionally, more detail on some material not covered in the chapter.
There has been a great deal of work on causality in philosophy, law, economics, and psychology. Although I have tried to cover the highlights, the bibliography is by no means exhaustive. Still, I hope that there is enough material there to guide the interested reader’s exploration of the literature.
The hypothesis that the dinosaur extinction was due to a meteor striking the earth was proposed by Luis and Walter Alvarez [Alvarez et al. 1980]. While originally viewed as quite radical, this hypothesis is getting increasing support from the evidence, including evidence of a meteor strike in Chicxulub in the Yucatan Peninsula at the appropriate time. Pälike [2013] provides a summary of research on the topic.
The distinction between actual causality and type causality has been related to the distinction between causes of effects—that is, the possible causes of a particular outcome—and effects of causes—that is, the possible effects of a given event. Some have claimed that reasoning about actual causality is equivalent to reasoning about causes of effects, because both typically focus on individual events (e.g., the particular outcome of interest), whereas reasoning about type causality is equivalent to reasoning about effects of causes, because when thinking of effects of causes, we are typically interested in understanding whether a certain type of behavior brings about a certain type of outcome. Although this may typically be the case, it is clearly not always the case; Livengood [2015] gives a number of examples that illustrate this point. Dawid [2007] argued that reasoning about effects of causes is typically forward-looking and reasoning about causes of effects is typically backward-looking. The idea that type causality is forward-looking and actual causality is backward-looking seems to have been first published by Hitchcock [2013], although as the work of Dawid [2007] shows, it seems to have been in the air for a while.
The exact relationship between actual and type causality has been a matter of some debate. Some have argued that two separate theories are needed (see, e.g., [Eells 1991; Good 1961a; Good 1961b; Sober 1984]); others (e.g., [Hitchcock 1995]) have argued for one basic notion. Statisticians have largely focused on type causality and effects of causes; Dawid, Faigman, and Fienberg [2014] discuss how statistical techniques can be used for causes of effects. My current feeling is that type causation arises from many instances of actual causation, so that actual causation is more fundamental, but nothing in this book hinges on that.
Work on causality goes back to Aristotle [Falcon 2014]. Hume [1748] arguably started more modern work on causality. Robinson [1962] discusses Hume’s two definitions of causality in more detail. Perhaps the best-known definition involving regularity (in the spirit of the first sentence in the earlier Hume quotation) is due to Mackie [1974], who introduced what has been called the INUS condition: A is a cause of B if A is an insufficient but necessary part of a condition that is itself unnecessary but sufficient for B. The basic intuition behind this condition is that A should be a cause of B if A is necessary and sufficient for B to happen, but there are many counterexamples to this simple claim. Ball A hitting B is not necessary for B to go into the goal, even in Figure 1.1(b); removing the brick would also work. Mackie modified this basic intuition by taking A to be a cause of B if there exist X and Y such that adding (A∧X) ∨Y is necessary and sufficient for B, but neither A nor X by itself is sufficient to entail B. If this definition is taken apart carefully, it gives us INUS:
Note that the notion of necessity and sufficiency used here is related to, but different from, that used when considering counterfactual theories of causality. While Mackie’s INUS condition is no longer viewed as an appropriate definition of causality (e.g., it has trouble with cases of preemption such as the rock-throwing example, where there is a backup ready to bring about the outcome in case what we would like to call the actual cause fails to do so), work on defining causality in terms of regularity still continues; Baumgartner [2013] and Strevens [2009] are recent exemplars.
I make no attempt to do justice to all the alternative approaches to defining causality; my focus is just the HP definition, which was introduced in [Halpern and Pearl 2001; Halpern and Pearl 2005a]. As I said, the HP definition is formalized carefully in Chapter 2. There is some discussion of alternative approaches to defining causality in the notes to Chapter 2. Paul and Hall [2013] provide a good overview of work on causality, along with a critical analysis of the strengths and weaknesses of various approaches.
The experiment with ball B hitting ball A is discussed by Gerstenberg, Goodman, Lagnado, and Tenenbaum [2014]. Figure 1.1 is taken from their paper (which also reports on a number of other related experiments).
The rock-throwing example is due to Lewis [2000]. It is but one of many examples of preemption in both the law and philosophy literatures.
Hart and Honoré [1985] discuss the but-for condition and, more generally, the use of actual causality in the law; it is the classic reference on the topic. Honoré [2010] and Moore [2009] provide more recent discussions. Lewis [1973a] initiated modern work in philosophy on counterfactual theories of causation; Menzies [2014] provides an overview of the work on the counterfactual approach to causation in philosophy. Sloman [2009] discusses how people ascribe causality, taking counterfactuals into account.
Although the focus in this book is on work on causality in philosophy, law, and psychology, causality also has a long tradition in other fields. The seminal work of Adam Smith [1994], considered a foundation of economics, is titled “An Inquiry into the Nature and Causes of the Wealth of Nations”. Hoover [2008] provides an overview of work on causality in economics. Statistics is, of course, very concerned with causal influence; Pearl [2009] provides an overview of work in statistics on causation. Discussion of causality in physics comes up frequently, particularly in the context of the Einstein-Podolsky-Rosen paradox, where the question is whether A can be a cause of B even though B happened so shortly after A that a signal traveling at the speed of light from A could not have reached B (see [Bell 1964]). More recently, (the HP definition of) causality has been applied in computer science; I discuss some of these applications in Chapter 8. The volume edited by Illari, Russo, and Williamson [2011] provides a broad overview of the role of causality in the social sciences, health sciences, and physical sciences.
The HP Definition of Causality
The fluttering of a butterfly’s wing in Rio de Janeiro, amplified by atmospheric currents, could cause a tornado in Texas two weeks later.
Edward Lorenz
There is only one constant, one universal. It is the only real truth. Causality. Action, reaction. Cause and effect.
Merovingian, The Matrix Reloaded
In this chapter, I go through the HP definition in detail. The HP definition is a formal, mathematical definition. Although this does add some initial overhead, it has an important advantage: it prevents ambiguity about whether A counts as a cause of B. There is no need, as in many other definitions, to try to understand how to interpret the words. For example, recall the INUS condition from the notes in Chapter 1. For A to be a cause of B under this definition, A has to be a necessary part of a condition that is itself unnecessary but insufficient for B. But what is a “condition”? The formalization of INUS suggests that it is a formula or set of formulas. Is there any constraint on this set? What language is it expressed in?
This lack of ambiguity is obviously critical if we want to apply causal reasoning in the law. But as we shall see in Chapter 8, it is equally important in other applications of causality, such as program verification, auditing, and database queries. However, even if there is no ambiguity about the definition, it does not follow that there can be no disagreement about whether A is a cause of B.
To understand how this can be the case, it is best to outline the general approach. The first step in the HP definition involves building a formal model in which causality can be determined unambiguously. Among other things, the model determines the language that is used to describe the world. We then define only what it means for A to be a cause of B in model M. It is possible to construct two closely related models M1 and M2 such that A is a cause of B in M1 but not in M2. I do not believe that there is, in general, a “right” model; in any case, the definition is silent on what makes one model better than another. (This is an important issue, however. I do think that there are criteria that can help judge whether one model is better than another; see below and Chapter 4 for more on this point.) Here we already see one instance where, even if there is agreement regarding the definition of causality, we can get disagreements regarding causality: there may be disagreement about which model better describes the real world. This is arguably a feature of the definition. It moves the question of actual causality to the right arena—debating which of two (or more) models of the world is a better representation of those aspects of the world that one wishes to capture and reason about. This, indeed, is the type of debate that goes on in informal (and legal) arguments all the time.
The model assumes that the world is described in terms of variables; these variables can take on various values. For example, if we are trying to determine whether a forest fire was caused by lightning or an arsonist, we can take the world to be described by three variables:
If we are considering a voting scenario where there are eleven voters voting for either Billy or Suzy, we can describe the world using twelve variables, V1, …, V11, W, where Vi = 0 if voter i voted for Billy and V1 = 1 if voter i voted for Suzy, for i = 1,…, 11, W = 0 if Billy wins, and W = 1 if Suzy wins.
In these two examples, all the variables are binary, that is, they take on only two values. There is no problem allowing a variable to have more than two possible values. For example, the variable Vi could be either 0, 1, or 2, where Vi = 2 if i does not vote; similarly, we could take W = 2 if the vote is tied, so neither Billy nor Suzy wins.
The choice of variables determines the language used to frame the situation. Although there is no “right” choice, clearly some choices are more appropriate than others. For example, if there is no variable corresponding to smoking in model M, then in M, smoking cannot be a cause of Sam’s lung cancer. Thus, if we want to consider smoking as a potential cause of lung cancer, M is an inappropriate model. (As an aside, the reader may note that here and elsewhere I put “right” in quotes; that is because it is not clear to me that the notion of being “right” is even well defined.)
Some variables may have a causal influence on others. This influence is modeled by a set of structural equations. For example, if we want to model the fact that if the arsonist drops a match or lightning strikes then a fire starts, we could use the variables MD, FF, and L as above, with the equation FF = max(L, MD); that is, the value of the variable FF is the maximum of the values of the variables MD and L. This equation says, among other things, that if MD = 0 and L = 1, then FF = 1. The equality sign in this equation should be thought of more like an assignment statement in programming languages; once we set the values of MD and L, the value of FF is set to their maximum. However, despite the equality, a forest fire starting some other way does not force the value of either MD or L to be 1.
Alternatively, if we want to model the fact that a fire requires both a lightning strike and a dropped match (perhaps the wood is so wet that it needs two sources of fire to get going), then the only change in the model is that the equation for FF becomes FF = min(L, MD); the value of FF is the minimum of the values of MD and L. The only way that FF = 1 is if both L = 1 and MD = 1.
Just a notational aside before going on: I sometimes identify binary variables with primitive propositions in propositional logic. And, as in propositional logic, the symbols ∧,∨, and ¬ are used to denote conjunction, disjunction, and negation, respectively. With that identification, instead of writing max(L, MD ), I write L ∨ MD; instead of writing min(L, MD), I write L ∧ MD; and instead of writing 1 − L or 1 − MD, I write L or MD. Most people seem to find the logic notation easier to absorb. I hope that the intention will be clear from context.
Going on with the forest-fire example, it is clear that both of these models are somewhat simplistic. Lightning does not always result in a fire, nor does dropping a lit match. One way of dealing with this would be to make the assignment statements probabilistic. For example, we could say that the probability that FF = 1 conditional on L = 1 is .8. I discuss this approach in more detail in Section 2.5. It is much simpler to think of all the equations as being deterministic and then use enough variables to capture all the conditions that determine whether there is a forest fire. One way to do this is simply to add those variables explicitly. For example, we could add variables that talk about the dryness of the wood, the amount of undergrowth, the presence of sufficient oxygen (fires do not start so easily on the top of high mountains), and so on. If a modeler does not want to add all these variables explicitly (the details may simply not be relevant to the analysis), then another alternative is to use a single variable, say U, which intuitively incorporates all the relevant factors, without describing them explicitly. The value of U would determine whether the lightning strikes and whether the match is dropped by the arsonist.
The value of U could also determine whether both the match and lightning are needed to start a fire or just one of them suffices. For simplicity, rather than using U in this way, I consider two causal models. In one, called the conjunctive model, both the match and lightning are needed to start the forest fire; in the other, called the disjunctive model, only one is needed. In each of these models, U determines only whether the lightning strakes and whether the match is dropped. Thus, I assume that U can take on four possible values of the form (i, j), where i and j are each either 0 or 1. Intuitively, i describes whether the external conditions are such that the lightning strikes (and encapsulates all such conditions, e.g., humidity and temperature), and j describes whether the arsonist drops the match (and thus encapsulates all the psychological conditions that determine this). For future reference, let U1 and U2 denote the components of the value of U in this example, so that if U = (i, j), then U1 = i and U2 = j.
Here I have assumed a single variable U that determines the values of both L and MD. I could have split U into two variables, say UL and UMD, where UL determines the value of L and UMD determines the value of MD. It turns out that whether we use a single variable with four possible values or two variables, each with two values, makes no real difference. (Other modeling choices can make a big difference—I return to this point below.)
It is reasonable to ask why I have chosen to describe the world in terms of variables and their values, related via structural equations. Using variables and their values is quite standard in fields such as statistics and econometrics for good reason; it is a natural way to describe situations. The examples later in this section should help make that point. It is also quite close to propositional logic; we can think of a primitive proposition in classical logic as a binary variable, whose values are either true or false. Although there may well be other reasonable ways of representing the world, this seems like a useful approach.
As for the use of structural equations, recall that my goal is to give a definition of actual causality in terms of counterfactuals. Certainly if the but-for test applies, so that, but for A, B would not have happened, I want the definition to declare that A is a cause of B. That means I need a model rich enough to capture the fact that, but for A, B would not have happened. Because I model the world in terms of variables and their values, the A and the B in the definition will be statements such as X = x and Y = y. Thus, I want to say that if X had taken on some value x′ different from x, then Y would not have had value y. To do this, I need a model that makes it possible to consider the effect of intervening on X and changing its value from x to x′. Describing the world in terms of variables and their values makes it easy to describe such interventions; using structural equations makes it easy to define the effect of an intervention.
This can be seen already in the forest-fire example. In the conjunctive model, if we see a forest fire, then we can say that if the arsonist hadn’t dropped a match, there would have been no forest fire. This follows in the model because setting MD = 0 makes FF = min(L, MD ) = 0.
Before going into further details, I give an example of the power of structural equations. Suppose that we are interested in the relationship between education, an employee’s skill level, and his salary. Suppose that education can affect skill level (but does not necessarily always do so, since a student may not pay attention or have poor teachers) and skill level affects salary. We can give a simplified model of this situation using four variables:
There are two relevant equations. The first says that education determines skill level, provided that the external conditions (determined by U) are favorable, and otherwise has no impact:
![[image]](images/dcleq0001.jpg)
The second says that skill level determines salary:
![[image]](images/dcleq0002.jpg)
Although this model significantly simplifies some complicated relationships, we can already use it to answer interesting questions. Suppose that, in fact, we observe that Fred has salary level 1. We can thus infer that U = E = SL = 1. We can ask what Fred’s salary level would have been had he attained education level 2. This amounts to intervening and setting E = 2. Since U = 1, it follows that SL = 2 and thus S = 2; Fred would have a high salary. Similarly, if we observe that Fred’s education level is 1 but his salary is low, then we can infer that U = 0 and SL = 0, and we can say that his salary would still be low even if he had an extra year of education.
A more sophisticated model would doubtless include extra factors and more sensitive dependencies. Still, even at this level, I hope it is clear that the structural equations framework can give reasonable answers.
When working with structural equations, it turns out to be conceptually useful to split the variables into two sets: the exogenous variables, whose values are determined by factors outside the model, and the endogenous variables, whose values are ultimately determined by the exogenous variables. In the forest-fire example, the variable U, which determines whether the lightning strikes and whether the arsonist drops a match, is exogenous; the variables FF, L, and MD are endogenous. The value of U determines the values of L and MD, which in turn determine the value of FF. We have structural equations for the three endogenous variables that describe how this is done. In general, there is a structural equation for each endogenous variable, but there are no equations for the exogenous variables; as I said, their values are determined by factors outside the model. That is, the model does not try to “explain” the values of the exogenous variables; they are treated as given.
The split between exogenous and endogenous variables has another advantage. The structural equations are all deterministic. As we shall see in Section 2.5, when we want to talk about the probability that A is a cause of B, we can do so quite easily by putting a probability distribution on the values of the exogenous variables. This gives us a way of talking about the probability of there being a fire if lightning strikes, while still using deterministic equations.
In any case, with this background, we can formally define a causal model M as a pair ![[image]](images/dcleq0003.jpg) , where
, where ![[image]](images/dcleq0004.jpg) is a signature, which explicitly lists the endogenous and exogenous variables and characterizes their possible values, and
is a signature, which explicitly lists the endogenous and exogenous variables and characterizes their possible values, and ![[image]](images/dcleq0005.jpg) defines a set of structural equations, relating the values of the variables. In the next two paragraphs, I define
defines a set of structural equations, relating the values of the variables. In the next two paragraphs, I define ![[image]](images/dcleq0006.jpg) and
and ![[image]](images/dcleq0007.jpg) formally; the definitions can be skipped by the less mathematically inclined reader.
formally; the definitions can be skipped by the less mathematically inclined reader.
A signature ![[image]](images/dcleq0008.jpg) is a tuple
is a tuple ![[image]](images/dcleq0009.jpg) , where
, where ![[image]](images/dcleq0010.jpg) is a set of exogenous variables,
is a set of exogenous variables, ![[image]](images/dcleq0011.jpg) is a set of endogenous variables, and
is a set of endogenous variables, and ![[image]](images/dcleq0012.jpg) associates with every variable Y
associates with every variable Y ![[image]](images/dcleq0013.jpg) a nonempty set
a nonempty set ![[image]](images/dcleq0014.jpg) of possible values for Y (i.e., the set of values over which Y ranges). As suggested earlier, in the forest-fire example, we can take
of possible values for Y (i.e., the set of values over which Y ranges). As suggested earlier, in the forest-fire example, we can take ![[image]](images/dcleq0015.jpg) ; that is, U is exogenous,
; that is, U is exogenous, ![[image]](images/dcleq0016.jpg) consists of the four possible values of U discussed earlier,
consists of the four possible values of U discussed earlier, ![[image]](images/dcleq0017.jpg) , and
, and ![[image]](images/dcleq0018.jpg) .
.
The function ![[image]](images/dcleq0019.jpg) associates with each endogenous variable
associates with each endogenous variable ![[image]](images/dcleq0020.jpg) a function denoted FX such that FX maps
a function denoted FX such that FX maps ![[image]](images/dcleq0021.jpg) to
to ![[image]](images/dcleq0022.jpg) . (Recall that
. (Recall that ![[image]](images/dcleq0023.jpg) is the set consisting of all the variables in either
is the set consisting of all the variables in either ![[image]](images/dcleq0024.jpg) or
or ![[image]](images/dcleq0025.jpg) that are not in {X}. The notation
that are not in {X}. The notation ![[image]](images/dcleq0026.jpg) denotes the cross-product of
denotes the cross-product of ![[image]](images/dcleq0027.jpg) , where Z ranges over the variables in
, where Z ranges over the variables in ![[image]](images/dcleq0028.jpg) ; thus, if
; thus, if ![[image]](images/dcleq0029.jpg) , then
, then ![[image]](images/dcleq0030.jpg) consists of tuples of the form (z1, …, zk), where zi is a possible value of Zi, for i = 1, …, k.) This mathematical notation just makes precise the fact that FX determines the value of X, given the values of all the other variables in
consists of tuples of the form (z1, …, zk), where zi is a possible value of Zi, for i = 1, …, k.) This mathematical notation just makes precise the fact that FX determines the value of X, given the values of all the other variables in ![[image]](images/dcleq0031.jpg) . In the running forest-fire example, FFF would depend on whether we are considering the conjunctive model (where both the lightning strike and dropped match are needed for the fire) or the disjunctive model (where only one of the two is needed). In the conjunctive model, as I have already noted, FFF (L, MD, U) = 1 iff (“iff” means “if and only if”—this standard abbreviation is used throughout the book) min(L, MD ) = 1; in the disjunctive model, FFF (L, MD, U ) = 1 iff max(L, MD) = 1. Note that, in both cases, the value of FFF is independent of U; it depends only on the values of L and MD. Put another way, this means that when we hold the values of L and MD fixed, changing the value of U has no effect on the value of FFF. While the values of MD and L do depend on the value of U, writing things in this way allows us to consider the effects of external interventions that may override U. For example, we can consider FFF (0, 1, (1, 1)); this tells us what happens if the lightning does not strike and the match is dropped, even if the value of U is such that L = 1. In what follows, we will be interested only in interventions on endogenous variables. As I said, we take the values of the exogenous variables as given, so do not intervene on them.
. In the running forest-fire example, FFF would depend on whether we are considering the conjunctive model (where both the lightning strike and dropped match are needed for the fire) or the disjunctive model (where only one of the two is needed). In the conjunctive model, as I have already noted, FFF (L, MD, U) = 1 iff (“iff” means “if and only if”—this standard abbreviation is used throughout the book) min(L, MD ) = 1; in the disjunctive model, FFF (L, MD, U ) = 1 iff max(L, MD) = 1. Note that, in both cases, the value of FFF is independent of U; it depends only on the values of L and MD. Put another way, this means that when we hold the values of L and MD fixed, changing the value of U has no effect on the value of FFF. While the values of MD and L do depend on the value of U, writing things in this way allows us to consider the effects of external interventions that may override U. For example, we can consider FFF (0, 1, (1, 1)); this tells us what happens if the lightning does not strike and the match is dropped, even if the value of U is such that L = 1. In what follows, we will be interested only in interventions on endogenous variables. As I said, we take the values of the exogenous variables as given, so do not intervene on them.
The notation FX (Y, Y′, U ) for the equation describing how the value of X depends on Y, Y′, and U is not terribly user-friendly. I typically simplify notation and write X = Y + U instead of FX (Y, Y′, U) = Y + U. (Note that the variable Y′ does not appear on the right-hand side of the equation. That means that the value of X does not depend on that of Y′.) With this simplified notation, the equations for the forest-fire example are L = U1, MD = U2, and either FF = min(L, MD ) or FF = max(L, MD), depending on whether we are considering the conjunctive or disjunctive model.
Although I may write something like X = Y + U, the fact that X is assigned Y + U does not imply that Y is assigned X − U; that is, FY (X, Y′, U ) = X − U does not necessarily hold. The equation X = Y + U implies that if Y = 3 and U = 2, then X = 5, regardless of how Y′ is set. Going back to the forest-fire example, setting FF = 0 does not mean that the match is “undropped”! This asymmetry in the treatment of the variables on the left- and right-hand sides of the equality sign means that (the value of) Y can depend on (the value of) X without X depending on Y. This, in turn, is why causality is typically asymmetric in the formal definition that I give shortly: if A is a cause of B, then B will typically not be a cause of A. (See the end of Section 2.7 for more discussion of this issue.)
As I suggested earlier, the key role of the structural equations is that they allow us to determine what happens if things had been other than they were, perhaps due to an external intervention; for example, the equations tell us what would happen if the arsonist had not dropped a match (even if in fact he did). This will be critical in defining causality.
Since a world in a causal model is described by the values of variables, understanding what would happen if things were other than they were amounts to asking what would happen if some variables were set to values perhaps different from their actual values. Setting the value of some variable X to x in a causal model ![[image]](images/dcleq0032.jpg) results in a new causal model denoted MX←x. In the new causal model, the equation for X is simple: X is just set to x; the remaining equations are unchanged. More formally,
results in a new causal model denoted MX←x. In the new causal model, the equation for X is simple: X is just set to x; the remaining equations are unchanged. More formally, ![[image]](images/dcleq0033.jpg) , where
, where ![[image]](images/dcleq0034.jpg) is the result of replacing the equation for X in
is the result of replacing the equation for X in ![[image]](images/dcleq0035.jpg) by X = x and leaving the remaining equations untouched. Thus, if MC is the conjunctive model of the forest fire, then in
by X = x and leaving the remaining equations untouched. Thus, if MC is the conjunctive model of the forest fire, then in ![[image]](images/dcleq0036.jpg) , the model that results from intervening in M C by having the arsonist not drop a match, the equation MD = U2 is replaced by MD = 0.
, the model that results from intervening in M C by having the arsonist not drop a match, the equation MD = U2 is replaced by MD = 0.
As I said in Chapter 1, the HP definition involves counterfactuals. The equations in a causal model can be given a straightforward counterfactual interpretation. An equation such as x = FX (u, y) should be thought of as saying that in a context where the exogenous variable U has value u, if Y were set to y by some means (not specified in the model), then X would take on the value x. As I noted earlier, when Y is set to y, this can override the value of Y according to the equations. For example, MD can be set to 0 even in a context where the exogenous variable U = (1, 1), so MD would be 1.
It may seem somewhat circular to use causal models, which clearly already encode causal relationships, to define causality. There is some validity to this concern. After all, how do we determine whether a particular equation holds? We might believe that dropping a lit match results in a forest burning in part because of our experience with lit matches and dry wood, and thus believe that a causal relationship holds between the lit match and the dry wood. We might also have a general theory of which this is a particular outcome, but there too, roughly speaking, the theory is being understood causally. Nevertheless, I would claim that this definition is useful. In many examples, there is general agreement as to the appropriate causal model. The structural equations do not express actual causality; rather, they express the effects of interventions or, more generally, of variables taking on values other than their actual values.
Of course, there may be uncertainty about the effects of interventions, just as there may be uncertainty about the true setting of the values of the exogenous variables in a causal model. For example, we may be uncertain about whether smoking causes cancer (this represents uncertainty about the causal model), uncertain about whether a particular patient Sam actually smoked (this is uncertainty about the value of the exogenous variables that determine whether Sam smokes), and uncertain about whether Sam’s brother Jack, who did smoke and got cancer, would have gotten cancer had he not smoked (this is uncertainty about the effect of an intervention, which amounts to uncertainty about the values of exogenous variables and possibly the equations). All this uncertainty can be described by putting a probability on causal models and on the values of the exogenous variables. We can then talk about the probability that A is a cause of B. (See Section 2.5 for further discussion of this point.)
Using (the equations in) a causal model, we can determine whether a variable Y is (in)dependent of variable X. Y depends on X if there is some setting of all the variables in ![[image]](images/dcleq0037.jpg) other than X and Y such that varying the value of X in that setting results in a variation in the value of Y; that is, there is a setting
other than X and Y such that varying the value of X in that setting results in a variation in the value of Y; that is, there is a setting ![[image]](images/dcleq0038.jpg) of the variables other than X and Y and values x and x′ of X such that
of the variables other than X and Y and values x and x′ of X such that ![[image]](images/dcleq0039.jpg) . (The
. (The ![[image]](images/dcleq0040.jpg) represents the values of all the other variables. This vector notation is a useful shorthand that is used throughout the book; I say more about it for readers unfamiliar with it at the end of the section.) Note that by “dependency” here I mean something closer to “immediate dependency” or “direct dependency”. This notion of dependency is not transitive; that is, if X1 depends on X2 and X2 depends on X3, then it is not necessarily the case that X1 depends on X3. If Y does not depend on X, then Y is independent of X.
represents the values of all the other variables. This vector notation is a useful shorthand that is used throughout the book; I say more about it for readers unfamiliar with it at the end of the section.) Note that by “dependency” here I mean something closer to “immediate dependency” or “direct dependency”. This notion of dependency is not transitive; that is, if X1 depends on X2 and X2 depends on X3, then it is not necessarily the case that X1 depends on X3. If Y does not depend on X, then Y is independent of X.
Whether Y depends on X may depend in part on the variables in the language. In the original description of the voting scenario, we had just twelve variables, and W depended on each of V1, …, V11. However, suppose that the votes are tabulated by a machine. We can add a variable T that describes that final tabulation of the machine, where T can have any value of the form (t1, t2), where t1 represents the number of votes for Billy and t2 represents the number of votes for Suzy (so that t1 and t2 are non-negative integers whose sum is 11). Now W depends only on T, while T depends on V1, …, V11.
In general, every variable can depend on every other variable. But in most interesting situations, each variable depends on relatively few other variables. The dependencies between variables in a causal model M can be described using a causal network (sometimes called a causal graph), consisting of nodes and directed edges. I often omit the exogenous variables from the graph. Thus, both Figure 2.1(a) (where the exogenous variable is included) and Figure 2.1(b) (where it is omitted) would be used to describe the forest-fire example. Figure 2.1(c) is yet another description of the forest-fire example, this time replacing the single exogenous variable U by an exogenous variable U1 that determines L and an exogenous variable U2 that determines MD. Again, Figure 2.1(b) is the causal graph that results when the exogenous variables in Figure 2.1(c) are omitted. Since all the “action” happens with the endogenous variables, Figure 2.1(b) really gives us all the information we need to analyze this example.
![[image]](images/fig2-1.jpg)
Figure 2.1: A graphical representation of structural equations.
The fact that there is a directed edge from U to both L and MD in Figure 2.1(a) (with the direction marked by the arrow) says that the value of the exogenous variable U affects the value of L and MD, but nothing else affects it. The directed edges from L and MD to FF say that only the values of MD and L directly affect the value of FF. (The value of U also affects the value of FF, but it does so indirectly, through its effect on L and MD.)
Causal networks convey only the qualitative pattern of dependence; they do not tell us how a variable depends on others. For example, the same causal network would be used for both the conjunctive and disjunctive models of the forest-fire example. Nevertheless, causal networks are useful representations of causal models.
I will be particularly interested in causal models where there are no circular dependencies. For example, it is not the case that X depends on Y and Y depends X or, more generally, that X1 depends on X2, which depends on X3, which depends on X4, which depends on X1. Informally, a model is said to be recursive (or acyclic) if there are no such dependency cycles (sometimes called feedback cycles) among the variables.
The intuition that the values of exogenous variables are determined by factors outside the model is formalized by requiring that an exogenous variable does not depend on any other variables. (Actually, nothing in the following discussion changes if we allow an exogenous variable to depend on other exogenous variables. All that matters is that an exogenous variable does not depend on any endogenous variables.) In a recursive model, we can say more about how the values of endogenous are determined. Specifically, the values of some of the endogenous variables depend only on the values of the exogenous variables. This is the case for the variables L and MD in the forest-fire example depicted in Figure 2.1. Think of these as the “first-level” endogenous variables. The values of the “second-level” endogenous variables depend only on the values of exogenous variables and the values of first-level endogenous variables. The variable FF is a second-level variable in this sense; its value is determined by that of L and MD, and these are first-level variables. We can then define third-level variables, fourth-level variables, and so on.
Actually, the intuition I have just given is for what I call a strongly recursive model. It is easy to see that in a strongly recursive model, the values of all variables are determined given a context, that is, a setting ![[image]](images/dcleq0041.jpg) for the exogenous variables in
for the exogenous variables in ![[image]](images/dcleq0042.jpg) . Given
. Given ![[image]](images/dcleq0043.jpg) , we can determine the values of the first-level variables using the equations; we can then determine the values of the second-level variables (whose values depend only on the context and the values of the first-level variables), then the third-level variables, and so on. The notion of a recursive model generalizes the definition of a strongly recursive model (every strongly recursive model is recursive, but the converse is not necessarily true) while still keeping this key feature of having the context determine the values of all the endogenous variables. In a recursive model, the partition of endogenous variables into first-level variables, second-level variables, and so on can depend on the context; in different contexts, the partition might be different. Moreover, in a recursive model, our definition guarantees that causality is asymmetric: it cannot be the case that A is a cause of B and B is a cause of A if A and B are distinct. (See the discussion at the end of Section 2.7.)
, we can determine the values of the first-level variables using the equations; we can then determine the values of the second-level variables (whose values depend only on the context and the values of the first-level variables), then the third-level variables, and so on. The notion of a recursive model generalizes the definition of a strongly recursive model (every strongly recursive model is recursive, but the converse is not necessarily true) while still keeping this key feature of having the context determine the values of all the endogenous variables. In a recursive model, the partition of endogenous variables into first-level variables, second-level variables, and so on can depend on the context; in different contexts, the partition might be different. Moreover, in a recursive model, our definition guarantees that causality is asymmetric: it cannot be the case that A is a cause of B and B is a cause of A if A and B are distinct. (See the discussion at the end of Section 2.7.)
The next four paragraphs provide a formal definition of recursive models. They can be skipped on a first reading.
Say that a model M is strongly recursive (or acyclic) if there is some partial order ⪯ on the endogenous variables in M (the ones in ![[image]](images/dcleq0044.jpg) ) such that unless X ⪯ Y, Y is not affected by X. Roughly speaking, X ⪯ Y denotes that X affects Y (think of “affects” here as the transitive closure of the direct dependency relation discussed earlier; X affects Y if there is some chain X1, …, Xk such that X = X1, Y = Xk, and Xi+1 directly depends on Xi for i = 1, …, k − 1. The fact that ⪯ is a partial order means that ⪯ is a reflexive, anti-symmetric, and transitive relation. Reflexivity means that X ⪯ X for each variable X—X affects X; anti-symmetry means that if X ⪯ Y and Y ⪯ X, then X = Y —if X affects Y and Y affects X, then we must have X = Y; finally, transitivity means that if X ⪯ Y and Y ⪯ Z, then X ⪯ Z—if X affects Y and Y affects Z, then X affects Z. Since ⪯ is partial, it may be the case that for some variables X and Y, neither X ⪯ Y nor Y ⪯ X holds; that is, X does not affect Y and Y does not affect X.
) such that unless X ⪯ Y, Y is not affected by X. Roughly speaking, X ⪯ Y denotes that X affects Y (think of “affects” here as the transitive closure of the direct dependency relation discussed earlier; X affects Y if there is some chain X1, …, Xk such that X = X1, Y = Xk, and Xi+1 directly depends on Xi for i = 1, …, k − 1. The fact that ⪯ is a partial order means that ⪯ is a reflexive, anti-symmetric, and transitive relation. Reflexivity means that X ⪯ X for each variable X—X affects X; anti-symmetry means that if X ⪯ Y and Y ⪯ X, then X = Y —if X affects Y and Y affects X, then we must have X = Y; finally, transitivity means that if X ⪯ Y and Y ⪯ Z, then X ⪯ Z—if X affects Y and Y affects Z, then X affects Z. Since ⪯ is partial, it may be the case that for some variables X and Y, neither X ⪯ Y nor Y ⪯ X holds; that is, X does not affect Y and Y does not affect X.
While reflexivity and transitivity seem to be natural properties of the “affects” relation, anti-symmetry is a nontrivial assumption. The fact that ⪯ is anti-symmetric and transitive means that there is no cycle of dependence between a collection X1, …, Xn of variables. It cannot be the case that X1 affects X2, X2 affects X3, …, Xn−1 affects Xn, and Xn affects X1. For then we would have X1 ⪯ X2, X2 ⪯ X3, …, Xn−1 Xn, and Xn ⪯ X1. By transitivity, we would have X2 ⪯ X1, violating anti-symmetry. A causal network corresponding to a causal model where there is no such cyclic dependence between the variables is acyclic. That is, there is no sequence of directed edges that both starts and ends at the same node.
A model M is recursive if, for each context (setting of the exogenous variables) ![[image]](images/dcleq0045.jpg) , there is a partial order
, there is a partial order ![[image]](images/dcleq0046.jpg) of the endogenous variables such that unless
of the endogenous variables such that unless ![[image]](images/dcleq0047.jpg) , Y is independent of X in
, Y is independent of X in ![[image]](images/dcleq0048.jpg) , where Y is independent of X in
, where Y is independent of X in ![[image]](images/dcleq0049.jpg) if, for all settings
if, for all settings ![[image]](images/dcleq0050.jpg) of the endogenous variables other than X and Y, and all values x and x′ of X,
of the endogenous variables other than X and Y, and all values x and x′ of X, ![[image]](images/dcleq0051.jpg) . If M is a strongly recursive model, then we can assume that all the partial orders
. If M is a strongly recursive model, then we can assume that all the partial orders ![[image]](images/dcleq0052.jpg) are the same; in a recursive model, they may differ. Example 2.3.3 below shows why it is useful to consider the more general notion of recursive model.
are the same; in a recursive model, they may differ. Example 2.3.3 below shows why it is useful to consider the more general notion of recursive model.
As I said, if M is a recursive causal model, then given a context ![[image]](images/dcleq0053.jpg) , there is a unique solution for all the equations. We simply solve for the variables in the order given by
, there is a unique solution for all the equations. We simply solve for the variables in the order given by ![[image]](images/dcleq0054.jpg) (where
(where ![[image]](images/dcleq0055.jpg) if
if ![[image]](images/dcleq0056.jpg) and X ≠ Y). The value of the variables that come first in the order, that is, the variables X such that there is no variable Y such that
and X ≠ Y). The value of the variables that come first in the order, that is, the variables X such that there is no variable Y such that ![[image]](images/dcleq0057.jpg) , depend only on the exogenous variables, so their value is immediately determined by the values of the exogenous variables. The values of variables later in the order can be determined from the equations once we have determined the values of all the variables earlier in the order.
, depend only on the exogenous variables, so their value is immediately determined by the values of the exogenous variables. The values of variables later in the order can be determined from the equations once we have determined the values of all the variables earlier in the order.
With the definition of recursive model under our belt, we can get back to the issue of choosing the “right” model. There are many nontrivial decisions to be made when choosing the causal model to describe a given situation. One significant decision is the set of variables used. As we shall see, the events that can be causes and those that can be caused are expressed in terms of these variables, as are all the intermediate events. The choice of variables essentially determines the “language” of the discussion; new events cannot be created on the fly, so to speak. In our running forest-fire example, the fact that there is no variable for unattended campfires means that the model does not allow us to consider unattended campfires as a cause of the forest fire.
Once the set of variables is chosen, the next step is to decide which are exogenous and which are endogenous. As I said earlier, the exogenous variables to some extent encode the background situation that we want to take as given. Other implicit background assumptions are encoded in the structural equations themselves. Suppose that we are trying to decide whether a lightning bolt or a match was the cause of the forest fire, and we want to take as given that there is sufficient oxygen in the air and the wood is dry. We could model the dryness of the wood by an exogenous variable D with values 0 (the wood is wet) and 1 (the wood is dry). (Of course, in practice, we may want to allow D to have more values, indicating the degree of dryness of the wood, but that level of complexity is unnecessary for the points I am trying to make here.) By making D exogenous, its value is assumed to be determined by external factors that are not being modeled. We could also take the amount of oxygen to be described by an exogenous variable (e.g., there could be a variable O with two values—0, for insufficient oxygen; and 1, for sufficient oxygen); alternatively, we could choose not to model oxygen explicitly at all. For example, suppose that we have, as before, a variable MD (match dropped by arsonist) and another variable WB (wood burning), with values 0 (it’s not) and 1 (it is). The structural equation FWB would describe the dependence of WB on D and MD. By setting FWB (1, 1) = 1, we are saying that the wood will burn if the lit match is dropped and the wood is dry. Thus, the equation is implicitly modeling our assumption that there is sufficient oxygen for the wood to burn. Whether the modeler should include O in the model depends on whether the modeler wants to consider contexts where the value of O is 0. If in all contexts relevant to the modeler there is sufficient oxygen, there is no point in cluttering up the model by adding the variable O (although adding it will not affect anything).
According to the definition of causality in Section 2.2, only endogenous variables can be causes or be caused. Thus, if no variables encode the presence of oxygen, or if it is encoded only in an exogenous variable, then oxygen cannot be a cause of the forest burning in that model. If we were to explicitly model the amount of oxygen in the air (which certainly might be relevant if we were analyzing fires on Mount Everest), then FWB would also take values of O as an argument, and the presence of sufficient oxygen might well be a cause of the wood burning, and hence the forest burning. Interestingly, in the law, there is a distinction between what are called conditions and causes. Under typical circumstances, the presence of oxygen would be considered a condition, and would thus not count as a cause of the forest burning, whereas the lightning would. While the of oxygen would be considered a condition and would thus not count as a cause of the forest burning, while the lightning would. Although the distinction is considered important, it does not seem to have been carefully formalized. One way of understanding it is in terms of exogenous versus endogenous variables: conditions are exogenous, (potential) causes are endogenous. I discuss an alternative approach to understanding the distinction, in terms of theories of normality, in Section 3.2.
It is not always straightforward to decide what the “right” causal model is in a given situation. What is the “right” set of variables to use? Which should be endogenous and which should be exogenous? As we shall see, different choices of endogenous variables can lead to different conclusions, although they seem to be describing exactly the same situation. And even after we have chosen the variables, how do we determine the equations that relate them? Given two causal models, how do we decide which is better?
These are all important questions. For now, however, I will ignore them. The definition of causality I give in the next section is relative to a model M and context ![[image]](images/dcleq0058.jpg) . A may be a cause of B relative to
. A may be a cause of B relative to ![[image]](images/dcleq0059.jpg) and not a cause of B relative to
and not a cause of B relative to ![[image]](images/dcleq0060.jpg) . Thus, the choice of model can have a significant impact in determining causality ascriptions. The definition is agnostic regarding the choice of model; it has nothing to say about whether the choice of variables or the structural equations used are in some sense “reasonable”. Of course, people may legitimately disagree about how well a particular causal model describes the world. Although the formalism presented here does not provide techniques to settle disputes about which causal model is the right one, at least it provides tools for carefully describing the differences between causal models, so that it should lead to more informed and principled decisions about those choices. That said, I do return to some of the issues raised earlier when discussing the examples in this section, and I discuss them in more detail in Chapter 4.
. Thus, the choice of model can have a significant impact in determining causality ascriptions. The definition is agnostic regarding the choice of model; it has nothing to say about whether the choice of variables or the structural equations used are in some sense “reasonable”. Of course, people may legitimately disagree about how well a particular causal model describes the world. Although the formalism presented here does not provide techniques to settle disputes about which causal model is the right one, at least it provides tools for carefully describing the differences between causal models, so that it should lead to more informed and principled decisions about those choices. That said, I do return to some of the issues raised earlier when discussing the examples in this section, and I discuss them in more detail in Chapter 4.
As promised, I conclude this section with a little more discussion of the vector notation, for readers unfamiliar with it. I use this notation throughout the book to denote sets of variables or their values. For example, if there are three exogenous variables, say U1, U2, and U3, and U1 = 0, U2 = 0, and U3 = 1, then I write U![[image]](images/dcleq0061.jpg) as an abbreviation of U1 = 0, U2 = 0, and U3 = 1. This vector notation is also used to describe the values
as an abbreviation of U1 = 0, U2 = 0, and U3 = 1. This vector notation is also used to describe the values ![[image]](images/dcleq0062.jpg) of a collection
of a collection ![[image]](images/dcleq0063.jpg) of endogenous variables. I deliberately abuse notation at times and view
of endogenous variables. I deliberately abuse notation at times and view ![[image]](images/dcleq0064.jpg) both as a set of variables and as a sequence of variables. For example, when I write
both as a set of variables and as a sequence of variables. For example, when I write ![[image]](images/dcleq0065.jpg) , then I am thinking of
, then I am thinking of ![[image]](images/dcleq0066.jpg) as the sequence (U1, U2, U3), and this equality means that U1 = 0, U2 = 0, and U3 = 1. However, in expressions such as
as the sequence (U1, U2, U3), and this equality means that U1 = 0, U2 = 0, and U3 = 1. However, in expressions such as ![[image]](images/dcleq0067.jpg) and
and ![[image]](images/dcleq0068.jpg) ,
, ![[image]](images/dcleq0069.jpg) should be understood as the corresponding unordered set {U1, U2, U3}. I hope that the intent is always clear from context. For the most part, readers who do not want to delve into details can just ignore the vector arrows.
should be understood as the corresponding unordered set {U1, U2, U3}. I hope that the intent is always clear from context. For the most part, readers who do not want to delve into details can just ignore the vector arrows.
2.2 A Formal Definition of Actual Cause
In this section, I give the HP definition of causality and show how it works in a number of examples. But before giving the definition, I have to define a formal language for describing causes.
2.2.1 A language for describing causality
To make the definition of actual causality precise, it is helpful to have a formal language for making statements about causality. The language is an extension of propositional logic, where the primitive events (i.e., primitive propositions) have the form X = x for an endogenous variable X and some possible value x of X. The primitive event MD = 0 says “the lit match is not dropped”; similarly, the primitive event L = 1 says “lightning occurred”. These primitive events can be combined using standard propositional connectives, such as ∧, ∨, and ¬. Thus, the formula MD = 0 ∨ L = 1 says “either the lit match is not dropped or lightning occurred”, MD = 0 ∧ L = 1 says “the lit match is not dropped and lightning occurred”, and ¬(L = 1) says “lightning did not occur” (which is equivalent to L = 0, given that the only possible values of L are 0 or 1). A Boolean combination of primitive events is a formula obtained by combining primitive events using ∧, ∨, and ¬. For example, ¬ (MD = 0 ∨ L = 1) ∧ WB = 1 is a Boolean combination of the primitive events MD = 0, L = 1, and WB = 1. The key novel feature in the language is that we can talk about interventions. A formula of the form ![[image]](images/dcleq0070.jpg) says that after intervening to set the variables in
says that after intervening to set the variables in ![[image]](images/dcleq0071.jpg) to
to ![[image]](images/dcleq0072.jpg) , X takes on the value x.
, X takes on the value x.
(A short aside: I am thinking of an event here as a subset of a state space; this is the standard usage in computer science and probability. Once I give semantics to causal formulas, it will be clear that we can associate a causal formula φ with a set of contexts—the set of context where φ is true—so it can indeed be identified with an event in this sense. In the philosophy literature, the use of the word “event” is somewhat different, and what counts as an event is contentious; see the notes at the end of this chapter and at the end of Chapter 4.)
Now for the formal details. Given a signature ![[image]](images/dcleq0073.jpg) , a primitive event is a formula of the form X = x, for
, a primitive event is a formula of the form X = x, for ![[image]](images/dcleq0074.jpg) and
and ![[image]](images/dcleq0075.jpg) . A causal formula (over
. A causal formula (over ![[image]](images/dcleq0076.jpg) ) is one of the form [Y1 ← y1, …, Yk ← yk]φ, where
) is one of the form [Y1 ← y1, …, Yk ← yk]φ, where
![[image]](images/dcleq0077.jpg) , and
, and![[image]](images/dcleq0078.jpg) .
.Such a formula is abbreviated as ![[image]](images/dcleq0079.jpg) , using the vector notation. The special case where k = 0 is abbreviated as [ ]φ or, more often, just φ. Intuitively, [Y1 ← y1, …, Yk ← yk]φ says that φ would hold if Yi were set to yi, for i = 1, …, k. It is worth emphasizing that the commas in [Y1 ← y1, …, Yk ← yk]φ are really acting like conjunctions; this says that if Y1 were set to y1 and … and Yk were set to yk, then φ would hold. I follow convention and use the comma rather than ∧. I write Yj ← yj rather than Yj = yj to emphasize that here Yj is assigned the value yj, as the result of an intervention. For
, using the vector notation. The special case where k = 0 is abbreviated as [ ]φ or, more often, just φ. Intuitively, [Y1 ← y1, …, Yk ← yk]φ says that φ would hold if Yi were set to yi, for i = 1, …, k. It is worth emphasizing that the commas in [Y1 ← y1, …, Yk ← yk]φ are really acting like conjunctions; this says that if Y1 were set to y1 and … and Yk were set to yk, then φ would hold. I follow convention and use the comma rather than ∧. I write Yj ← yj rather than Yj = yj to emphasize that here Yj is assigned the value yj, as the result of an intervention. For ![[image]](images/dcleq0080.jpg) , let
, let ![[image]](images/dcleq0081.jpg) consist of all Boolean combinations of causal formulas, where the variables in the formulas are taken from
consist of all Boolean combinations of causal formulas, where the variables in the formulas are taken from ![[image]](images/dcleq0082.jpg) and the sets of possible values of these variables are determined by
and the sets of possible values of these variables are determined by ![[image]](images/dcleq0083.jpg) .
.
The language above lets us talk about interventions. What we need next is a way of defining the semantics of causal formulas: that is, a way of determining when a causal formula is true. A causal formula ψ is true or false in a causal model, given a context. I call a pair ![[image]](images/dcleq0084.jpg) consisting of a causal model M and context
consisting of a causal model M and context ![[image]](images/dcleq0085.jpg) a causal setting. I write
a causal setting. I write ![[image]](images/dcleq0086.jpg) if the causal formula ψ is true in the causal setting
if the causal formula ψ is true in the causal setting ![[image]](images/dcleq0087.jpg) . For now, I restrict attention to recursive models, where, given a context, there are no cyclic dependencies. In a recursive model,
. For now, I restrict attention to recursive models, where, given a context, there are no cyclic dependencies. In a recursive model, ![[image]](images/dcleq0088.jpg) if the value of X is x once we set the exogenous variables to
if the value of X is x once we set the exogenous variables to ![[image]](images/dcleq0089.jpg) . Here I am using the fact that, in a recursive model, the values of all the endogenous variables are determined by the context. If ψ is an arbitrary Boolean combination of primitive events, then whether
. Here I am using the fact that, in a recursive model, the values of all the endogenous variables are determined by the context. If ψ is an arbitrary Boolean combination of primitive events, then whether ![[image]](images/dcleq0090.jpg) can be determined by the usual rules of propositional logic. For example,
can be determined by the usual rules of propositional logic. For example, ![[image]](images/dcleq0091.jpg) if either
if either ![[image]](images/dcleq0092.jpg) or
or ![[image]](images/dcleq0093.jpg) .
.
Using causal models makes it easy to give the semantics of formulas of the form ![[image]](images/dcleq0094.jpg) and, more generally,
and, more generally, ![[image]](images/dcleq0095.jpg) . Recall that the latter formula says that, after intervening to set the variables in
. Recall that the latter formula says that, after intervening to set the variables in ![[image]](images/dcleq0096.jpg) to
to ![[image]](images/dcleq0097.jpg) , ψ holds. Given a model M, the model that describes the result of this intervention is
, ψ holds. Given a model M, the model that describes the result of this intervention is ![[image]](images/dcleq0098.jpg) . Thus,
. Thus,
![[image]](images/dcleq0099.jpg)
The mathematics just formalizes the intuition that the formula ![[image]](images/dcleq0100.jpg) is true in the causal setting
is true in the causal setting ![[image]](images/dcleq0101.jpg) exactly if the formula ψ is true in the model that results from the intervention, in the same context
exactly if the formula ψ is true in the model that results from the intervention, in the same context ![[image]](images/dcleq0102.jpg) .
.
For example, if Md is the disjunctive model for the forest fire described earlier, then (M d, (1, 1)) ⊨ [MD ← 0](FF = 1): even if the arsonist is somehow prevented from dropping the match, the forest burns (thanks to the lightning); that is, ![[image]](images/dcleq0103.jpg) . Similarly, (Md, (1, 1)) ⊨ [L ← 0](FF = 1). However, (M d, (1, 1)) ⊨ [L ← 0; MD ← 0](FF = 0): if the arsonist does not drop the lit match and the lightning does not strike, then the forest does not burn.
. Similarly, (Md, (1, 1)) ⊨ [L ← 0](FF = 1). However, (M d, (1, 1)) ⊨ [L ← 0; MD ← 0](FF = 0): if the arsonist does not drop the lit match and the lightning does not strike, then the forest does not burn.
The notation ![[image]](images/dcleq0104.jpg) is standard in the logic and philosophy communities. It is, unfortunately, not at all standard in other communities, such as statistics and econometrics. Although notation is not completely standard in these communities, the general approach has been to suppress the model M and make the context
is standard in the logic and philosophy communities. It is, unfortunately, not at all standard in other communities, such as statistics and econometrics. Although notation is not completely standard in these communities, the general approach has been to suppress the model M and make the context ![[image]](images/dcleq0105.jpg) an argument of the endogenous variables. Thus, for example, instead of writing
an argument of the endogenous variables. Thus, for example, instead of writing ![[image]](images/dcleq0106.jpg) , in these communities they would write
, in these communities they would write ![[image]](images/dcleq0107.jpg) . (Sometimes the exogenous variables are also suppressed, or taken as given, so just X = x is written.) More interestingly, instead of
. (Sometimes the exogenous variables are also suppressed, or taken as given, so just X = x is written.) More interestingly, instead of ![[image]](images/dcleq0108.jpg) , in these communities they would write
, in these communities they would write ![[image]](images/dcleq0109.jpg) . Although the latter notation, which I henceforth call statisticians’ notation (although it is more widespread), is clearly more compact, the compactness occasionally comes at the price of clarity. For example, in the disjunctive forest-fire example, what does FF 0(1, 1) = 1 mean? Is it (M d, (1, 1)) ⊨ [MD ← 0](FF = 1) or (Md, (1, 1)) = [L ← 0](FF = 1)? This problem can be solved by adding the variable being intervened on to the subscript if it is necessary to remove ambiguity, writing, for example, FF L←0(1, 1) = 0. Things get more complicated when we want to write
. Although the latter notation, which I henceforth call statisticians’ notation (although it is more widespread), is clearly more compact, the compactness occasionally comes at the price of clarity. For example, in the disjunctive forest-fire example, what does FF 0(1, 1) = 1 mean? Is it (M d, (1, 1)) ⊨ [MD ← 0](FF = 1) or (Md, (1, 1)) = [L ← 0](FF = 1)? This problem can be solved by adding the variable being intervened on to the subscript if it is necessary to remove ambiguity, writing, for example, FF L←0(1, 1) = 0. Things get more complicated when we want to write ![[image]](images/dcleq0110.jpg) , where ϕ is a Boolean combination of primitive events, or when there are several causal models in the picture and it is important to keep track of them. That said, there are many situations when writing something like Yx(u) = y is completely unambiguous, and it is certainly more compact. To make things easier for those used to this notation, I translate various statements into statisticians’ notation, particularly those where it leads to more compact formulations. This will hopefully have the added advantage of making both notations familiar to all communities.
, where ϕ is a Boolean combination of primitive events, or when there are several causal models in the picture and it is important to keep track of them. That said, there are many situations when writing something like Yx(u) = y is completely unambiguous, and it is certainly more compact. To make things easier for those used to this notation, I translate various statements into statisticians’ notation, particularly those where it leads to more compact formulations. This will hopefully have the added advantage of making both notations familiar to all communities.
2.2.2 The HP definition of actual causality
I now give the HP definition of actual causality.
The types of events that the HP definition allows as actual causes are ones of the form X1 = x1 ∧ … ∧ Xk = xk—that is, conjunctions of primitive events; this is often abbreviated as ![[image]](images/dcleq0111.jpg) . The events that can be caused are arbitrary Boolean combinations of primitive events. The definition does not allow statements of the form “A or A′ is a cause of B,” although this could be treated as being equivalent to “either A is a cause of B or A′ is a cause of B”. However, statements such as “A is a cause of either B or B′” are allowed; this is not equivalent to “either A is a cause of B or A is a cause of B′”.
. The events that can be caused are arbitrary Boolean combinations of primitive events. The definition does not allow statements of the form “A or A′ is a cause of B,” although this could be treated as being equivalent to “either A is a cause of B or A′ is a cause of B”. However, statements such as “A is a cause of either B or B′” are allowed; this is not equivalent to “either A is a cause of B or A is a cause of B′”.
Note that this means that the relata of causality (what can be a cause and what can be caused) depend on the language. It is also worth remarking that there is a great deal of debate in the philosophical literature about the relata of causality. Although it is standard in that literature to take the relata of causality to be events, exactly what counts as an event is also a matter of great debate. I do not delve further into these issues here; see the notes at the end of the chapter for references and a little more discussion.
Although I have been talking up to now about “the” HP definition of causality, I will actually consider three definitions, all with the same basic structure. Judea Pearl and I started with a relatively simple definition that gradually became more complicated as we discovered examples that our various attempts could not handle. One of the examples was discovered after our definition was published in a conference paper. So we updated the definition for the journal version of the paper. Later work showed that the problem that caused us to change the definition was not as serious as originally thought. However, recently I have considered a definition that is much simpler than either of the two previous versions, which has the additional merit of dealing better with a number of problems. It is not clear that the third definition is the last word. Moreover, showing how the earlier definitions deal with the various problems that have been posed lends further insight into the difficulties and subtleties involved with finding a definition of causality. Thus, I consider all three definitions in this book. Following Einstein, my goal is to make things as simple as possible, but no simpler!
Like the definition of truth on which it depends, the HP definition of causality is relative to a causal setting. All three variants of the definition consist of three clauses. The first and third are simple and straightforward, and the same for all the definitions. All the work is done by the second clause; this is where the definitions differ.
Definition 2.2.1 ![[image]](images/dcleq0112.jpg) is an actual cause of φ in the causal setting
is an actual cause of φ in the causal setting ![[image]](images/dcleq0113.jpg) if the following three conditions hold:
if the following three conditions hold:
AC1. ![[image]](images/dcleq0114.jpg) and
and ![[image]](images/dcleq0115.jpg) .
.
AC2. See below.
AC3. ![[image]](images/dcleq0116.jpg) is minimal; there is no strict subset
is minimal; there is no strict subset ![[image]](images/dcleq0117.jpg) of
of ![[image]](images/dcleq0118.jpg) such that
such that ![[image]](images/dcleq0119.jpg) satisfies conditions AC1 and AC2, where
satisfies conditions AC1 and AC2, where ![[image]](images/dcleq0120.jpg) is the restriction of
is the restriction of ![[image]](images/dcleq0121.jpg) to the variables in
to the variables in ![[image]](images/dcleq0122.jpg) . ■
. ■
AC1 just says that ![[image]](images/dcleq0123.jpg) cannot be considered a cause of φ unless both
cannot be considered a cause of φ unless both ![[image]](images/dcleq0124.jpg) and φ actually happen. (I am implicitly taking
and φ actually happen. (I am implicitly taking ![[image]](images/dcleq0125.jpg) to characterize the “actual world” here.) AC3 is a minimality condition, which ensures that only those elements of the conjunction
to characterize the “actual world” here.) AC3 is a minimality condition, which ensures that only those elements of the conjunction ![[image]](images/dcleq0126.jpg) that are essential are considered part of a cause; inessential elements are pruned. Without AC3, if dropping a lit match qualified as a cause of the forest fire, then dropping a match and sneezing would also pass the tests of AC1 and AC2. AC3 serves here to strip “sneezing” and other irrelevant, over-specific details from the cause. AC3 can be viewed as capturing part of the spirit of the INUS condition; roughly speaking, it says that all the primitive events in the cause are necessary for the effect.
that are essential are considered part of a cause; inessential elements are pruned. Without AC3, if dropping a lit match qualified as a cause of the forest fire, then dropping a match and sneezing would also pass the tests of AC1 and AC2. AC3 serves here to strip “sneezing” and other irrelevant, over-specific details from the cause. AC3 can be viewed as capturing part of the spirit of the INUS condition; roughly speaking, it says that all the primitive events in the cause are necessary for the effect.
It is now time to bite the bullet and look at AC2. In the first two versions of the HP definition, AC2 consists of two parts. I start by considering the first of them, denoted AC2(a). AC2(a) is a necessity condition. It says that for X = x to be a cause of ϕ, there must be a value x′ in the range of X such that if X is set to x′, φ no longer holds. This is the but-for clause; but for the fact that X = x occurred, φ would not have occurred. As we saw in the Billy-Suzy rock-throwing example in Chapter 1, the naive but-for clause will not suffice. We must be allowed to apply it under certain contingencies, that is, under certain counterfactual settings, where some variables are set to values other than those they take in the actual situation or held to certain values while other variables change. For example, in the case of Suzy and Billy, we consider a contingency where Billy does not throw.
Here is the formal version of the necessity condition:
AC2(a). There is a partition of ![[image]](images/dcleq0127.jpg) (the set of endogenous variables) into two disjoint subsets
(the set of endogenous variables) into two disjoint subsets ![[image]](images/dcleq0128.jpg) and
and ![[image]](images/dcleq0129.jpg) (so that
(so that ![[image]](images/dcleq0130.jpg) ) with
) with ![[image]](images/dcleq0131.jpg) and a setting
and a setting ![[image]](images/dcleq0132.jpg) and
and ![[image]](images/dcleq0133.jpg) of the variables in
of the variables in ![[image]](images/dcleq0134.jpg) and
and ![[image]](images/dcleq0135.jpg) , respectively, such that
, respectively, such that
![[image]](images/dcleq0136.jpg)
Using statisticians’ notation, if φ is ![[image]](images/dcleq0137.jpg) , then the displayed formula becomes
, then the displayed formula becomes ![[image]](images/dcleq0138.jpg) .
.
Roughly speaking, AC2(a) says that the but-for condition holds under the contingency ![[image]](images/dcleq0139.jpg) . We can think of the variables in
. We can think of the variables in ![[image]](images/dcleq0140.jpg) as making up the “causal path” from
as making up the “causal path” from ![[image]](images/dcleq0141.jpg) to φ. Intuitively, changing the value of some variable in
to φ. Intuitively, changing the value of some variable in ![[image]](images/dcleq0142.jpg) results in changing the value(s) of some variable(s) in
results in changing the value(s) of some variable(s) in ![[image]](images/dcleq0143.jpg) , which results in the values of some other variable(s) in
, which results in the values of some other variable(s) in ![[image]](images/dcleq0144.jpg) being changed, which finally results in the truth value of φ changing. (Whether we can think of the variables in
being changed, which finally results in the truth value of φ changing. (Whether we can think of the variables in ![[image]](images/dcleq0145.jpg) as making up a causal path from some variable in
as making up a causal path from some variable in ![[image]](images/dcleq0146.jpg) to some variable in φ turns out to depend in part on which variant of the HP definition we consider. See Section 2.9 for a formalization and more discussion.) The remaining endogenous variables, the ones in
to some variable in φ turns out to depend in part on which variant of the HP definition we consider. See Section 2.9 for a formalization and more discussion.) The remaining endogenous variables, the ones in ![[image]](images/dcleq0147.jpg) , are off to the side, so to speak, but may still have an indirect effect on what happens.
, are off to the side, so to speak, but may still have an indirect effect on what happens.
Unfortunately, AC1, AC2(a), and AC3 do not suffice for a good definition of causality. In the rock-throwing example, with just AC1, AC2(a), and AC3, Billy would be a cause of the bottle shattering. We need a sufficiency condition to block Billy. The sufficiency condition used in the original definition, roughly speaking, requires that if the variables in ![[image]](images/dcleq0148.jpg) and an arbitrary subset
and an arbitrary subset ![[image]](images/dcleq0149.jpg) of other variables on the causal path (i.e., besides those in
of other variables on the causal path (i.e., besides those in ![[image]](images/dcleq0150.jpg) ) are held at their values in the actual context (where the value of a variable Y in the actual context is the value y∗ such that (M, u) ⊨ Y = y∗; the values of the variables in
) are held at their values in the actual context (where the value of a variable Y in the actual context is the value y∗ such that (M, u) ⊨ Y = y∗; the values of the variables in ![[image]](images/dcleq0151.jpg) in the actual context is
in the actual context is ![[image]](images/dcleq0152.jpg) , by AC1), then φ holds even if
, by AC1), then φ holds even if ![[image]](images/dcleq0153.jpg) is set to
is set to ![[image]](images/dcleq0154.jpg) (the setting for
(the setting for ![[image]](images/dcleq0155.jpg) used in AC2(a)). This is formalized by the following condition:
used in AC2(a)). This is formalized by the following condition:
AC2(bo). If ![[image]](images/dcleq0156.jpg) is such that
is such that ![[image]](images/dcleq0157.jpg) , then for all subsets
, then for all subsets ![[image]](images/dcleq0158.jpg) of
of ![[image]](images/dcleq0159.jpg) , we have
, we have
![[image]](images/dcleq0160.jpg)
Again, taking φ to be ![[image]](images/dcleq0161.jpg) , in statisticians’ notation this becomes “if
, in statisticians’ notation this becomes “if ![[image]](images/dcleq0162.jpg) , then for all subsets
, then for all subsets ![[image]](images/dcleq0163.jpg) of
of ![[image]](images/dcleq0164.jpg) , we have
, we have ![[image]](images/dcleq0165.jpg) .” It is important to write at least the
.” It is important to write at least the ![[image]](images/dcleq0166.jpg) explicitly in the subscript here, since we are quantifying over it.
explicitly in the subscript here, since we are quantifying over it.
Note that, due to setting ![[image]](images/dcleq0167.jpg) to
to ![[image]](images/dcleq0168.jpg) , the values of the variables in
, the values of the variables in ![[image]](images/dcleq0169.jpg) may change. AC2(bo) says that this change does not affect φ; φ continues to be true. Indeed, ϕ continues to be true even if some variables in
may change. AC2(bo) says that this change does not affect φ; φ continues to be true. Indeed, ϕ continues to be true even if some variables in ![[image]](images/dcleq0170.jpg) are forced to their original values.
are forced to their original values.
Before going on, I need to make a brief technical digression to explain a slight abuse of notation in AC2(bo). Suppose that ![[image]](images/dcleq0171.jpg) ,
, ![[image]](images/dcleq0172.jpg) , and
, and ![[image]](images/dcleq0173.jpg) . Then
. Then ![[image]](images/dcleq0174.jpg) is intended to be an abbreviation for Z1 ← 1; that is, I am ignoring the second component of
is intended to be an abbreviation for Z1 ← 1; that is, I am ignoring the second component of ![[image]](images/dcleq0175.jpg) here. More generally, when I write
here. More generally, when I write ![[image]](images/dcleq0176.jpg) , I am picking out the values in
, I am picking out the values in ![[image]](images/dcleq0177.jpg) that correspond to the variables in
that correspond to the variables in ![[image]](images/dcleq0178.jpg) and ignoring those that correspond to the variables in
and ignoring those that correspond to the variables in ![[image]](images/dcleq0179.jpg) . I similarly write
. I similarly write ![[image]](images/dcleq0180.jpg) if
if ![[image]](images/dcleq0181.jpg) is a subset of
is a subset of ![[image]](images/dcleq0182.jpg) .
.
For reasons that will become clearer in Example 2.8.1, the original definition was updated to use a stronger version of AC2(bo). Sufficiency is now required to hold if the variables in any subset ![[image]](images/dcleq0183.jpg) of
of ![[image]](images/dcleq0184.jpg) are set to the values in
are set to the values in ![[image]](images/dcleq0185.jpg) (as well as the variables in any subset
(as well as the variables in any subset ![[image]](images/dcleq0186.jpg) of
of ![[image]](images/dcleq0187.jpg) being set to their values in the actual context). Taking
being set to their values in the actual context). Taking ![[image]](images/dcleq0188.jpg) and
and ![[image]](images/dcleq0189.jpg) as in AC2(a) (and AC2(bo)), here is the updated definition:
as in AC2(a) (and AC2(bo)), here is the updated definition:
AC2(bu). If ![[image]](images/dcleq0190.jpg) is such that
is such that ![[image]](images/dcleq0191.jpg) , then for all subsets
, then for all subsets ![[image]](images/dcleq0192.jpg) of
of ![[image]](images/dcleq0193.jpg) and subsets
and subsets ![[image]](images/dcleq0194.jpg) of
of ![[image]](images/dcleq0195.jpg) , we have
, we have ![[image]](images/dcleq0196.jpg) .
.
In statisticians’ notation, this becomes “if ![[image]](images/dcleq0197.jpg) , then for all subsets
, then for all subsets ![[image]](images/dcleq0198.jpg) of
of ![[image]](images/dcleq0199.jpg) and
and ![[image]](images/dcleq0200.jpg) v of
v of ![[image]](images/dcleq0201.jpg) , we have
, we have ![[image]](images/dcleq0202.jpg) .” Again, we need to write the variables in the subscript here.
.” Again, we need to write the variables in the subscript here.
The only difference between AC2(bo) and AC2(bu) lies in the clause “for all subsets ![[image]](images/dcleq0203.jpg) of
of ![[image]](images/dcleq0204.jpg) ”: AC2(bu) must hold even if only a subset
”: AC2(bu) must hold even if only a subset ![[image]](images/dcleq0205.jpg) of the variables in
of the variables in ![[image]](images/dcleq0206.jpg) are set to their values in
are set to their values in ![[image]](images/dcleq0207.jpg) . This means that the variables in
. This means that the variables in ![[image]](images/dcleq0208.jpg) essentially act as they do in the real world; that is, their values are determined by the structural equations, rather than being set to their values in
essentially act as they do in the real world; that is, their values are determined by the structural equations, rather than being set to their values in ![[image]](images/dcleq0209.jpg) .
.
The superscripts o and u in AC2(bo) and AC2(bu) are intended to denote “original” and “updated”.
I conclude by considering the simpler modified definition. This definition is motivated by the intuition that only what happens in the actual situation should matter. Thus, the only settings of variables allowed are ones that occur in the actual situation. Specifically, the modified definition simplifies AC2(a) by requiring that the only setting ![[image]](images/dcleq0210.jpg) of the variables in
of the variables in ![[image]](images/dcleq0211.jpg) that can be considered is the value of these variables in the actual context. Here is the modified AC2(a), denoted AC2(am) (the m stands for “modified”):
that can be considered is the value of these variables in the actual context. Here is the modified AC2(a), denoted AC2(am) (the m stands for “modified”):
AC2(am). There is a set ![[image]](images/dcleq0212.jpg) of variables in
of variables in ![[image]](images/dcleq0213.jpg) and a setting
and a setting ![[image]](images/dcleq0214.jpg) of the variables in
of the variables in ![[image]](images/dcleq0215.jpg) such that if
such that if ![[image]](images/dcleq0216.jpg) , then
, then
![[image]](images/dcleq0217.jpg)
That is, we can show the counterfactual dependence of φ on ![[image]](images/dcleq0218.jpg) by keeping the variables in
by keeping the variables in ![[image]](images/dcleq0219.jpg) fixed at their actual values. In statisticians’ notation (with φ being
fixed at their actual values. In statisticians’ notation (with φ being ![[image]](images/dcleq0220.jpg) ), this becomes “if
), this becomes “if ![[image]](images/dcleq0221.jpg) , then
, then ![[image]](images/dcleq0222.jpg) ”.
”.
It is easy to see that AC2(bo) holds if all the variables in ![[image]](images/dcleq0223.jpg) are fixed at their values in the actual context: because
are fixed at their values in the actual context: because ![[image]](images/dcleq0224.jpg) records the value of the variables in
records the value of the variables in ![[image]](images/dcleq0225.jpg) in the actual context, if is (re)set to
in the actual context, if is (re)set to ![[image]](images/dcleq0226.jpg) , its value in the actual context, then φ must hold (since, by AC1,
, its value in the actual context, then φ must hold (since, by AC1, ![[image]](images/dcleq0227.jpg) and φ both hold in the actual context); that is, we have
and φ both hold in the actual context); that is, we have ![[image]](images/dcleq0228.jpg) if
if ![[image]](images/dcleq0229.jpg) is the value of the variables in
is the value of the variables in ![[image]](images/dcleq0230.jpg) in the actual context. For similar reasons, AC2(bu) holds if all the variables in
in the actual context. For similar reasons, AC2(bu) holds if all the variables in ![[image]](images/dcleq0231.jpg) are fixed at their values in the actual context. Thus, there is no need for an analogue to AC2(bo) or AC2(bu) in the modified definition. This shows that the need for a sufficiency condition arises only if we are considering contingencies that differ from the actual setting in AC2(a). It is also worth noting that the modified definition does not need to mention
are fixed at their values in the actual context. Thus, there is no need for an analogue to AC2(bo) or AC2(bu) in the modified definition. This shows that the need for a sufficiency condition arises only if we are considering contingencies that differ from the actual setting in AC2(a). It is also worth noting that the modified definition does not need to mention ![[image]](images/dcleq0232.jpg) (although
(although ![[image]](images/dcleq0233.jpg) can be taken to be the complement of
can be taken to be the complement of ![[image]](images/dcleq0234.jpg) ).
).
For future reference, for all variants of the HP definition, the tuple ![[image]](images/dcleq0235.jpg) in AC2 is said to be a witness to the fact that
in AC2 is said to be a witness to the fact that ![[image]](images/dcleq0236.jpg) is a cause of φ. (I take the witness to be
is a cause of φ. (I take the witness to be ![[image]](images/dcleq0237.jpg) in the special case that
in the special case that ![[image]](images/dcleq0238.jpg) .)
.)
As I said, AC3 is a minimality condition. Technically, just as there are three versions of AC2, there are three corresponding versions of AC3. For example, in the case of the modified definition, AC3 should really say “there is no subset of ![[image]](images/dcleq0239.jpg) satisfying AC1 and AC2(am)”. I will not bother writing out these versions of AC3; I hope that the intent is clear whenever I refer to AC3.
satisfying AC1 and AC2(am)”. I will not bother writing out these versions of AC3; I hope that the intent is clear whenever I refer to AC3.
If I need to specify which variant of the HP definition I am considering, I will say that ![[image]](images/dcleq0240.jpg) is a cause of φ according to the original (resp., updated, modified) HP definition. If
is a cause of φ according to the original (resp., updated, modified) HP definition. If ![[image]](images/dcleq0241.jpg) is a cause of φ according to all three variants, I often just say “
is a cause of φ according to all three variants, I often just say “![[image]](images/dcleq0242.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dcleq0243.jpg) ”. Each conjunct in
”. Each conjunct in ![[image]](images/dcleq0244.jpg) is called part of a cause of φ in context
is called part of a cause of φ in context ![[image]](images/dcleq0245.jpg) . As we shall see, what we think of as causes in natural language correspond to parts of causes, especially with the modified HP definition. Indeed, it may be better to use a term such as “complete cause” for what I have been calling cause and then reserve “cause” for what I have called “part of a cause”. I return to this point after looking at a few examples.
. As we shall see, what we think of as causes in natural language correspond to parts of causes, especially with the modified HP definition. Indeed, it may be better to use a term such as “complete cause” for what I have been calling cause and then reserve “cause” for what I have called “part of a cause”. I return to this point after looking at a few examples.
Actually, although ![[image]](images/dcleq0246.jpg) is an abbreviation for the conjunction X1 = x1 ∧…∧Xk = xk, when we talk about
is an abbreviation for the conjunction X1 = x1 ∧…∧Xk = xk, when we talk about ![[image]](images/dcleq0247.jpg) being a cause of φ (particularly for the modified HP definition), it might in some ways be better to think of the disjunction. Roughly speaking,
being a cause of φ (particularly for the modified HP definition), it might in some ways be better to think of the disjunction. Roughly speaking, ![[image]](images/dcleq0248.jpg) is a cause of φ if it is the case that if none of the variables in
is a cause of φ if it is the case that if none of the variables in ![[image]](images/dcleq0249.jpg) had their actual value, then φ might not have occurred. However, if
had their actual value, then φ might not have occurred. However, if ![[image]](images/dcleq0250.jpg) has more than one variable, then just changing the value of a single variable in
has more than one variable, then just changing the value of a single variable in ![[image]](images/dcleq0251.jpg) (or, indeed, any strict subset of the variables in
(or, indeed, any strict subset of the variables in ![[image]](images/dcleq0252.jpg) ) is not enough by itself to bring about ¬φ (given the context). Thus, there is a sense in which the disjunction can be viewed as a but-for cause of φ. This will be clearer when we see the examples.
) is not enough by itself to bring about ¬φ (given the context). Thus, there is a sense in which the disjunction can be viewed as a but-for cause of φ. This will be clearer when we see the examples.
Note that all three variants of the HP definition declare X = x a cause of itself in (M, u) as long as (M, u) = X = x. This does not seem to me so unreasonable. At any rate, it seems fairly harmless, so I do not bother excluding it (although nothing would change if we did exclude it).
At this point, ideally, I would prove a theorem showing that some variant of the HP definition of actual causality is the “right” definition of actual causality. But I know of no way to argue convincingly that a definition is the “right” one; the best we can hope to do is to show that it is useful. As a first step, I show that all the definitions agree in the simplest and arguably most common case: but-for causes. Formally, say that X = x is a but-for cause of φ in ![[image]](images/dcleq0253.jpg) if AC1 holds (so that
if AC1 holds (so that ![[image]](images/dcleq0254.jpg) and there exists some x′ such that
and there exists some x′ such that ![[image]](images/dcleq0255.jpg) . Note here I am assuming that the cause is a single conjunct.
. Note here I am assuming that the cause is a single conjunct.
Proposition 2.2.2 If X = x is a but-for cause of Y = y in ![[image]](images/dcleq0256.jpg) , then X = x is a cause of Y = y according to all three variants of the HP definition.
, then X = x is a cause of Y = y according to all three variants of the HP definition.
Proof: Suppose that X = x is a but-for cause of Y = y. There must be a possible value x′ of X such that ![[image]](images/dcleq0257.jpg) . Then (∅, ∅, x′) (i.e.,
. Then (∅, ∅, x′) (i.e., ![[image]](images/dcleq0258.jpg) and X = x′) is a witness to X = x being a cause of φ for all three variants of the definition. Thus, AC2(a) and AC2(am) hold if we take
and X = x′) is a witness to X = x being a cause of φ for all three variants of the definition. Thus, AC2(a) and AC2(am) hold if we take ![[image]](images/dcleq0259.jpg) . Since
. Since ![[image]](images/dcleq0260.jpg) , if
, if ![[image]](images/dcleq0261.jpg) , where
, where ![[image]](images/dcleq0262.jpg) , then it is easy to see that
, then it is easy to see that ![[image]](images/dcleq0263.jpg) : since X = x and
: since X = x and ![[image]](images/dcleq0264.jpg) in the (unique) solution to the equations in context
in the (unique) solution to the equations in context ![[image]](images/dcleq0265.jpg) , this is still the case in the unique solution to the equations in MX←x. For similar reasons,
, this is still the case in the unique solution to the equations in MX←x. For similar reasons, ![[image]](images/dcleq0266.jpg) for all subsets
for all subsets ![[image]](images/dcleq0267.jpg) of
of ![[image]](images/dcleq0268.jpg) . (See Lemma 2.10.2, where these statements are formalized.) Thus, AC2(bo) holds. Because
. (See Lemma 2.10.2, where these statements are formalized.) Thus, AC2(bo) holds. Because ![[image]](images/dcleq0269.jpg) v, AC2(bu) follows immediately from AC2(bo). ■
v, AC2(bu) follows immediately from AC2(bo). ■
Of course, the definitions do not always agree. Other connections between the definitions are given in the following theorem. In the statement of the theorem, the notation ![[image]](images/dcleq0270.jpg) denotes the cardinality of
denotes the cardinality of ![[image]](images/dcleq0271.jpg) .
.
Theorem 2.2.3
(a)If X = x is part of a cause of φ in ![[image]](images/dcleq0272.jpg) according to the modified HP definition, then X = x is a cause of φ in
according to the modified HP definition, then X = x is a cause of φ in ![[image]](images/dcleq0273.jpg) according to the original HP definition.
according to the original HP definition.
(b)If X = x is part of a cause of φ in ![[image]](images/dcleq0274.jpg) according to the modified HP definition, then X = x is a cause of φ in
according to the modified HP definition, then X = x is a cause of φ in ![[image]](images/dcleq0275.jpg) according to the updated HP definition.
according to the updated HP definition.
(c)If X = x is part of a cause of φ in ![[image]](images/dcleq0276.jpg) according to the updated HP definition, then X = x is a cause of φ in
according to the updated HP definition, then X = x is a cause of φ in ![[image]](images/dcleq0277.jpg) according to the original HP definition.
according to the original HP definition.
(d)If ![[image]](images/dcleq0278.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dcleq0279.jpg) according to the original HP definition, then
according to the original HP definition, then ![[image]](images/dcleq0280.jpg) (i.e.,
(i.e., ![[image]](images/dcleq0281.jpg) is a singleton).
is a singleton).
Of course, (a) follows from (b) and (c); I state it separately just to emphasize the relations. Although it may not look like it at first glance, part (d) is quite similar in spirit to parts (a), (b), and (c); an equivalent reformulation of (d) is: “If X = x is part of a cause of φ in ![[image]](images/dcleq0282.jpg) according to the original HP definition, then X = x is a cause of φ in
according to the original HP definition, then X = x is a cause of φ in ![[image]](images/dcleq0283.jpg) according to the original HP definition.” Call this statement (d′). Clearly (d) implies (d′). For the converse, suppose that (d′) holds,
according to the original HP definition.” Call this statement (d′). Clearly (d) implies (d′). For the converse, suppose that (d′) holds, ![[image]](images/dcleq0284.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dcleq0285.jpg) , and
, and ![[image]](images/dcleq0286.jpg) . Then if X = x is a conjunct of
. Then if X = x is a conjunct of ![[image]](images/dcleq0287.jpg) , by (d′), X = x is a cause of φ in
, by (d′), X = x is a cause of φ in ![[image]](images/dcleq0288.jpg) . But by AC3, this can hold only if X = x is the only conjunct of
. But by AC3, this can hold only if X = x is the only conjunct of ![[image]](images/dcleq0289.jpg) , so
, so ![[image]](images/dcleq0290.jpg) .
.
Parts (a), (b), and (c) of Theorem 2.2.3 show that, in a sense, the original HP definition is the most permissive of the three and the modified HP definition is the most restrictive, with the updated HP definition lying somewhere in between. The converses of (a), (b), and (c) do not hold. As Example 2.8.1 shows, if X = x is a cause of φ according to the original HP definition, it is not, in general, part of a cause according to the modified or updated HP definition. In this example, we actually do not want causality to hold, so the example can be viewed as showing that the original definition is too permissive (although this claim is not quite as clear as it may appear at first; see the discussion in Section 2.8). Example 2.8.2 shows that part of a cause according to the updated HP definition need not be (part of) a cause according to the modified HP definition.
The bottom line here is that, although these definitions often agree, they do not always agree. It is typically on the most problematic examples on which they disagree. This is perhaps not surprising given that the original definition was updated and modified precisely to handle such examples. However, even in cases where the original definition seems to give “wrong” answers, there are often ways of dealing with the problem that do not require modifying the definition. Moreover, the fact that causes are always singletons with the original definition makes it attractive in some ways. The jury is still out on what the “right” definition of causality is. Although my current preference is the modified HP definition, I will consider all three definitions throughout the book. Despite the extra burden for the reader (for which I apologize in advance!), I think doing so gives a deeper insight into the subtleties of causality.
The proof of Theorem 2.2.3 can be found in Section 2.10.1. I recommend that the interested reader defer reading the proof until after going through the examples in the next section, since they provide more intuition for the definitions.
Because I cannot prove a theorem showing that (some variant of) the HP definition is the “right” definition of causality, all I can do to argue that the definition is reasonable is to show how it works in some of the examples that have proved difficult for other definitions to handle. That is one of the goals of this section. I also give examples that illustrate the subtle differences between the variants of the HP definition. I start with a few basic examples mainly intended to show how the definition works.
Example 2.3.1 For the forest-fire example, I consider two causal models, Mc and Md, for the conjunctive and disjunctive cases, respectively. These models were described earlier; the endogenous variables are L, MD, and FF, and U is the only exogenous variable. In both cases, I want to consider the context (1, 1), so the lightning strikes and the arsonist drops the match. In the conjunctive model, both the lightning and the dropped match are but-for causes of the forest fire; if either one had not occurred, the fire would not have happened. Hence, by Proposition 2.2.2, both L = 1 and MD = 1 are causes of FF = 1 in (Mc, (1, 1)) according to all three variants of the definition. By AC3, it follows that L = 1 MD = 1 is not a cause of FF = 1 in (M c, (1, 1)). This already shows that causes might not be unique; there may be more than one cause of a given outcome.
However, in the disjunctive case, there are differences. With the original and updated definition, again, we have that both L = 1 and MD = 1 are causes of FF = 1 in (M d, (1, 1)). I give the argument in the case of L = 1; the argument for MD = 1 is identical. Clearly (Md, (1, 1)) = FF = 1 and (Md, (1, 1)) = L = 1; in the context (1, 1), the lightning strikes and the forest burns down. Thus, AC1 is satisfied. AC3 is trivially satisfied: since ![[image]](images/dcleq0291.jpg) consists of only one element, L,
consists of only one element, L, ![[image]](images/dcleq0292.jpg) must be minimal.
must be minimal.
For AC2, as suggested earlier, let ![[image]](images/dcleq0293.jpg) ,
, ![[image]](images/dcleq0294.jpg) , x′ = 0, and w = 0. Clearly, (Md, (1, 1)) ⊨ [L ← 0, MD ← 0](FF = 1); if the lightning does not strike and the match is not dropped, the forest does not burn down, so AC2(a) is satisfied. To see the effect of the lightning, we must consider the contingency where the match is not dropped; AC2(a) allows us to do that by setting MD to 0. (Note that setting L and MD to 0 overrides the effects of U; this is critical.) Moreover,
, x′ = 0, and w = 0. Clearly, (Md, (1, 1)) ⊨ [L ← 0, MD ← 0](FF = 1); if the lightning does not strike and the match is not dropped, the forest does not burn down, so AC2(a) is satisfied. To see the effect of the lightning, we must consider the contingency where the match is not dropped; AC2(a) allows us to do that by setting MD to 0. (Note that setting L and MD to 0 overrides the effects of U; this is critical.) Moreover,
![[image]](images/dcleq0295.jpg)
in context (1, 1), if the lightning strikes, then the forest burns down even if the lit match is not dropped, so AC2(bo) and AC2(bu) are satisfied. (Note that since ![[image]](images/dcleq0296.jpg) , the only subsets of
, the only subsets of ![[image]](images/dcleq0297.jpg) are the empty set and the singleton set consisting of just FF; similarly, since
are the empty set and the singleton set consisting of just FF; similarly, since ![[image]](images/dcleq0298.jpg) , the only subsets of
, the only subsets of ![[image]](images/dcleq0299.jpg) are the empty set and the singleton set consisting of MD itself. Thus, we have considered all the relevant cases here.)
are the empty set and the singleton set consisting of MD itself. Thus, we have considered all the relevant cases here.)
This argument fails in the case of the modified definition because the setting MD = 0 is not allowed. The only witnesses that can be considered are ones where ![[image]](images/dcleq0300.jpg) has the value it does in the actual context; in the actual context here, MD = 1. So, with the modified definition, neither L = 1 nor MD = 1 is a cause. However, it is not hard to see that L = 1 ∧ MD = 1 is a cause of FF = 1. This shows why it is critical to consider only single conjuncts in Proposition 2.2.2 and Theorem 2.2.3 is worded in terms of parts of causes. Although L = 1 ∧ MD = 1 is a cause of FF = 1 according to the modified HP definition, it is not a cause according to either the original or updated HP definition. In contrast, L = 1 and MD = 1 are both parts of a cause of FF = 1 according to all three definitions.
has the value it does in the actual context; in the actual context here, MD = 1. So, with the modified definition, neither L = 1 nor MD = 1 is a cause. However, it is not hard to see that L = 1 ∧ MD = 1 is a cause of FF = 1. This shows why it is critical to consider only single conjuncts in Proposition 2.2.2 and Theorem 2.2.3 is worded in terms of parts of causes. Although L = 1 ∧ MD = 1 is a cause of FF = 1 according to the modified HP definition, it is not a cause according to either the original or updated HP definition. In contrast, L = 1 and MD = 1 are both parts of a cause of FF = 1 according to all three definitions.
It is arguably a feature of the original and updated HP definition that they call both L = 1 and MD = 1 causes of FF = 1. Calling the conjunction L = 1 ∧ MD = 1 a cause of FF = 1 does not seem to accord with natural language usage. There are two ways to address this concern. As I suggested earlier, with the modified HP definition, it may be better to think of parts of causes as coming closer to what we call causes in natural language. That would already deal with this concern. A second approach, which I also hinted at earlier, is to observe that it may be better to think of the disjunction L = 1 ∨ MD = 1 as being the cause. Indeed, we can think of MD = 1 ∨ L = 1 as a but-for cause of FF = 1; if it does not hold, then it must be the case both L = 0 and MD = 0, so there is no fire. The reader should keep in mind both of these ways of thinking of conjunctive causes with the modified HP definition.
As we shall see, the notion of responsibility, discussed in Chapter 6, allows the original and updated HP definition to distinguish these two scenarios, as does the notion of sufficient cause, discussed in Section 2.6. ■
This simple example already reveals some of the power of the HP definition. The case where the forest fire is caused by either the lightning or the dropped match (this is said to be a case of overdetermination in the literature) cannot be handled by the simple but-for definition used in the law. It seems reasonable to call both the lightning and the dropped match causes, or at least parts of causes. We certainly wouldn’t want to say that there is no cause, as a naive application of the but-for definition would do. (However, as I noted above, if we allow disjunctive causes, then a case can be made that the disjunction L = 1 ∨ MD = 1 is a but-for cause of the forest fire.) Overdetermination occurs frequently in legal cases; a victim may be shot by two people, for example. It occurs in voting as well; I look at this a little more carefully in the following example.
Example 2.3.2 Consider the voting scenario discussed earlier where there are 11 voters. If Suzy wins 6–5, then all the definitions agree that each of the voters for Suzy is a cause of Suzy’s victory; indeed, they are all but-for causes. But suppose that Suzy wins 11–0. Here we have overdetermination. The original and updated HP definition would still call each of the voters a cause of Suzy winning; the witness involves switching the votes of 5 voters. Since the modified HP definition does not allow such switching, according to the modified HP definition, any subset of six voters is a cause of Suzy winning (and every individual is part of a cause). Again, if we think of the subset as being represented by a disjunction, it can be thought of as a but-for cause of Suzy winning. If all six voters had switched their votes to Billy, then Suzy would not have won. Minimality holds; if a set of fewer than six voters had voted for Billy, then Suzy would still have won. ■
We do have an intuition that a voter for Suzy is somehow “less” of a cause of the victory in an 11–0 victory than in a 6–5 victory. This intuition is perhaps most compatible with the modified HP definition. In this case, ![[image]](images/dcleq0301.jpg) is a cause of φ if
is a cause of φ if ![[image]](images/dcleq0302.jpg) is a minimal set of variables whose values have to change for ¬φ to hold. The bigger
is a minimal set of variables whose values have to change for ¬φ to hold. The bigger ![[image]](images/dcleq0303.jpg) is, the less of a cause each of its conjuncts is. I return to this issue when I discuss responsibility in Chapter 6.
is, the less of a cause each of its conjuncts is. I return to this issue when I discuss responsibility in Chapter 6.
Example 2.3.3 Now I (finally!) consider the rock-throwing example, where Suzy and Billy both throw rocks at a bottle, but Suzy’s hits the bottle, and Billy’s doesn’t (although it would have hit had Suzy’s not hit first). We get the desired result—that Suzy’s throw is a cause, but Billy’s is not—but only if we model the story appropriately. Consider first a coarse causal model, with three endogenous variables:
For simplicity, assume that there is one exogenous variable u, which determines whether Billy and Suzy throw. (In most of the subsequent examples, I omit the exogenous variable in both the description of the story and the corresponding causal network.) Take the formula for BS to be such that the bottle shatters if either Billy or Suzy throws; that is, BS = BT ∨ ST. (I am implicitly assuming that Suzy and Billy never miss if they throw. Also, I follow the fairly standard mathematics convention of saying “if” rather than “if and only if” in definitions; clearly, the equation is saying that the bottle shatters if and only if either Billy or Suzy throws.) For future reference, I call this model ![[image]](images/dcleq0304.jpg) (where RT stands for “rock throwing”).
(where RT stands for “rock throwing”).
BT and ST play symmetric roles in ![[image]](images/dcleq0305.jpg) ; there is nothing to distinguish them. Not surprisingly, both Billy’s throw and Suzy’s throw are classified as causes of the bottle shattering in
; there is nothing to distinguish them. Not surprisingly, both Billy’s throw and Suzy’s throw are classified as causes of the bottle shattering in ![[image]](images/dcleq0306.jpg) in the context u where Suzy and Billy both throw according to the original and updated HP definition (the conjunction ST = 1 ∧ BT = 1 is the cause according to the modified HP definition). The argument is essentially identical to that used for the disjunctive model of the forest-fire example, where either the lightning or the dropped match is enough to start the fire. Indeed, the causal network describing this situation looks like that in Figure 2.1, with ST and BT replacing L and MD. For convenience, I redraw the network here. As I said earlier, here and in later figures, I typically omit the exogenous variable(s).
in the context u where Suzy and Billy both throw according to the original and updated HP definition (the conjunction ST = 1 ∧ BT = 1 is the cause according to the modified HP definition). The argument is essentially identical to that used for the disjunctive model of the forest-fire example, where either the lightning or the dropped match is enough to start the fire. Indeed, the causal network describing this situation looks like that in Figure 2.1, with ST and BT replacing L and MD. For convenience, I redraw the network here. As I said earlier, here and in later figures, I typically omit the exogenous variable(s).
![[image]](images/fig2-2.jpg)
Figure 2.2: MRT —a naive model for the rock-throwing example.
The trouble with MRT is that it cannot distinguish the case where both rocks hit the bottle simultaneously (in which case it would be reasonable to say that both ST = 1 and BT = 1 are causes of BS = 1) from the case where Suzy’s rock hits first. MRT has to be refined to express this distinction. One way is to invoke a dynamic model. Although this can be done (see the notes at the end of the chapter for more discussion), a simpler way to gain the expressiveness needed here is to allow BS to be three-valued, with values 0 (the bottle doesn’t shatter), 1 (it shatters as a result of being hit by Suzy’s rock), and 2 (it shatters as a result of being hit by Billy’s rock). I leave it to the reader to check that ST = 1 is a cause of BS = 1, but BT = 1 is not (if Suzy doesn’t throw but Billy does, then we would have BS = 2). To some extent, this solves our problem. But it borders on cheating; the answer is almost programmed into the model by invoking the relation “as a result of” in the definition of BS = 2, which requires the identification of the actual cause.
A more useful choice is to add two new variables to the model:
We now modify the equations as follows:
Thus, Billy’s throw hits if Billy throws and Suzy’s rock doesn’t hit. The last equation implicitly assumes that Suzy throws slightly ahead of Billy, or slightly harder.
Call this model ![[image]](images/dcleq0307.jpg) .
. ![[image]](images/dcleq0308.jpg) is described by the graph in Figure 2.3 (where again the exogenous variables are omitted). The asymmetry between BH and SH (in particular, the fact that Billy’s throw doesn’t hit the bottle if Suzy throws) is modeled by the fact that there is an edge from SH to BH but not one in the other direction; BH depends (in part) on SH but not vice versa.
is described by the graph in Figure 2.3 (where again the exogenous variables are omitted). The asymmetry between BH and SH (in particular, the fact that Billy’s throw doesn’t hit the bottle if Suzy throws) is modeled by the fact that there is an edge from SH to BH but not one in the other direction; BH depends (in part) on SH but not vice versa.
![[image]](images/fig2-3.jpg)
Figure 2.3: ![[image]](images/dcleq0309.jpg) —a better model for the rock-throwing example.
—a better model for the rock-throwing example.
Taking u to be the context where Billy and Suzy both throw, according to all three variants of the HP definition, ST = 1 is a cause of BS = 1 in ![[image]](images/dcleq0310.jpg) , but BT = 1 is not. To see that ST = 1 is a cause according to the original and updated HP definition, note that it is immediate that AC1 and AC3 hold. To see that AC2 holds, one possibility is to choose
, but BT = 1 is not. To see that ST = 1 is a cause according to the original and updated HP definition, note that it is immediate that AC1 and AC3 hold. To see that AC2 holds, one possibility is to choose ![[image]](images/dcleq0311.jpg) ,
, ![[image]](images/dcleq0312.jpg) , and w = 0. When BT is set to 0, BS tracks ST: if Suzy throws, the bottle shatters, and if she doesn’t throw, the bottle does not shatter. It immediately follows that AC2(a) and AC2(bo) hold. AC2(bu) is equivalent to AC2(bo) in this case, since
, and w = 0. When BT is set to 0, BS tracks ST: if Suzy throws, the bottle shatters, and if she doesn’t throw, the bottle does not shatter. It immediately follows that AC2(a) and AC2(bo) hold. AC2(bu) is equivalent to AC2(bo) in this case, since ![[image]](images/dcleq0313.jpg) is a singleton.
is a singleton.
To see that BT = 1 is not a cause of BS = 1 in ![[image]](images/dcleq0314.jpg) , we must check that there is no partition of the endogenous variables into sets
, we must check that there is no partition of the endogenous variables into sets ![[image]](images/dcleq0315.jpg) and
and ![[image]](images/dcleq0316.jpg) that satisfies AC2. Attempting the symmetric choice with
that satisfies AC2. Attempting the symmetric choice with ![[image]](images/dcleq0317.jpg) ,
, ![[image]](images/dcleq0318.jpg) , and w = 0 violates AC2(bo) and AC2(bu). To see this, take
, and w = 0 violates AC2(bo) and AC2(bu). To see this, take ![[image]](images/dcleq0319.jpg) . In the context where Suzy and Billy both throw, BH = 0. If BH is set to 0, then the bottle does not shatter if Billy throws and Suzy does not. It is precisely because, in this context, Suzy’s throw hits the bottle and Billy’s does not that we declare Suzy’s throw to be the cause of the bottle shattering. AC2(bo) and AC2(bu) capture that intuition by forcing us to consider the contingency where BH = 0 (i.e., where BH takes on its actual value), despite the fact that Billy throws.
. In the context where Suzy and Billy both throw, BH = 0. If BH is set to 0, then the bottle does not shatter if Billy throws and Suzy does not. It is precisely because, in this context, Suzy’s throw hits the bottle and Billy’s does not that we declare Suzy’s throw to be the cause of the bottle shattering. AC2(bo) and AC2(bu) capture that intuition by forcing us to consider the contingency where BH = 0 (i.e., where BH takes on its actual value), despite the fact that Billy throws.
Of course, just checking that this particular partition into ![[image]](images/dcleq0320.jpg) and
and ![[image]](images/dcleq0321.jpg) does not make BT = 1 a cause does not suffice to establish that BT = 1 is not a cause according to the original or updated definitions; we must check all possible partitions. I just sketch the argument here: The key is to consider whether BH is in
does not make BT = 1 a cause does not suffice to establish that BT = 1 is not a cause according to the original or updated definitions; we must check all possible partitions. I just sketch the argument here: The key is to consider whether BH is in ![[image]](images/dcleq0322.jpg) or
or ![[image]](images/dcleq0323.jpg) . If BH is in
. If BH is in ![[image]](images/dcleq0324.jpg) , then how we set BT has no effect on the value of BS: If BH is set to 0, then the value of BS is determined by the value of ST; and if BH is set to 1, then BS = 1 no matter what BT is. (It may seem strange to intervene and set BH to 1 if BT = 0. It means that somehow Billy hits the bottle even if he doesn’t throw. Such “miraculous” interventions are allowed by the definition; part of the motivation for the notion of normality considered in Chapter 3 is to minimize their usage.) This shows that we cannot have BH in
, then how we set BT has no effect on the value of BS: If BH is set to 0, then the value of BS is determined by the value of ST; and if BH is set to 1, then BS = 1 no matter what BT is. (It may seem strange to intervene and set BH to 1 if BT = 0. It means that somehow Billy hits the bottle even if he doesn’t throw. Such “miraculous” interventions are allowed by the definition; part of the motivation for the notion of normality considered in Chapter 3 is to minimize their usage.) This shows that we cannot have BH in ![[image]](images/dcleq0325.jpg) . If BH is in
. If BH is in ![[image]](images/dcleq0326.jpg) , then we get the same problem with AC2(bo) or AC2(bu) as above; it is easy to see that at least one of SH or ST must be in
, then we get the same problem with AC2(bo) or AC2(bu) as above; it is easy to see that at least one of SH or ST must be in ![[image]](images/dcleq0327.jpg) , and
, and ![[image]](images/dcleq0328.jpg) must be such that whichever is in
must be such that whichever is in ![[image]](images/dcleq0329.jpg) is set to 0.
is set to 0.
Note that, in this argument, it is critical that in AC2(bo) and AC2(bu) we allow setting an arbitrary subset of variables in ![[image]](images/dcleq0330.jpg) to their original values. There is a trivial reason for this: if we set all variables in
to their original values. There is a trivial reason for this: if we set all variables in ![[image]](images/dcleq0331.jpg) to their original values in
to their original values in ![[image]](images/dcleq0332.jpg) , then, among other things, we will set BS to 1. We will never be able to show that Billy’s throw is not a cause if BS is set to 1. But even requiring that all the variables in
, then, among other things, we will set BS to 1. We will never be able to show that Billy’s throw is not a cause if BS is set to 1. But even requiring that all the variables in ![[image]](images/dcleq0333.jpg) be set to their original values does not work. For suppose that we take
be set to their original values does not work. For suppose that we take ![[image]](images/dcleq0334.jpg) and take
and take ![[image]](images/dcleq0335.jpg) such that ST = 0. Clearly AC2(a) holds because if BT = 0, then BS = 0. But if all the variables in
such that ST = 0. Clearly AC2(a) holds because if BT = 0, then BS = 0. But if all the variables in ![[image]](images/dcleq0336.jpg) are set to their original values, then SH is set to 1, so the bottle shatters. To show that BT = 1 is not a cause, we must be able to set BH to its original value of 0 while keeping SH at 0. Setting BH to 0 captures the intuition that Billy’s throw is not a cause because, in the actual world, his rock did not hit the bottle (BH = 0).
are set to their original values, then SH is set to 1, so the bottle shatters. To show that BT = 1 is not a cause, we must be able to set BH to its original value of 0 while keeping SH at 0. Setting BH to 0 captures the intuition that Billy’s throw is not a cause because, in the actual world, his rock did not hit the bottle (BH = 0).
Finally, consider the modified HP definition. Here things are much simpler. In this case, taking ![[image]](images/dcleq0337.jpg) does not work to show that ST = 1 is a cause of BS = 1; we are not allowed to change BT from 1 to 0. However, we can take
does not work to show that ST = 1 is a cause of BS = 1; we are not allowed to change BT from 1 to 0. However, we can take ![[image]](images/dcleq0338.jpg) . Fixing BH at 0 (its setting in the actual context), if ST is set to 0, then BS = 0, that is, (M, u) ⊨ [ST ← 0, BH ← 0](BS = 0). Thus, ST = 1 is a cause of BS = 1 according to the modified HP definition. (Taking
. Fixing BH at 0 (its setting in the actual context), if ST is set to 0, then BS = 0, that is, (M, u) ⊨ [ST ← 0, BH ← 0](BS = 0). Thus, ST = 1 is a cause of BS = 1 according to the modified HP definition. (Taking ![[image]](images/dcleq0339.jpg) would also have worked to show that ST = 1 is a cause of BS = 1 according to the original and updated HP definition. Indeed, by Theorem 2.2.3, showing that ST = 1 is a cause of BS = 1 according to the modified definition suffices to show that it is also a cause according to the original and updated definition. I went through the argument for the original and updated definition because the more obvious choice for
would also have worked to show that ST = 1 is a cause of BS = 1 according to the original and updated HP definition. Indeed, by Theorem 2.2.3, showing that ST = 1 is a cause of BS = 1 according to the modified definition suffices to show that it is also a cause according to the original and updated definition. I went through the argument for the original and updated definition because the more obvious choice for ![[image]](images/dcleq0340.jpg) in that case is {BT}, and it works under those definitions.) But now it is also easy to check that BT = 1 is not a cause of BS = 1 according to the modified HP definition. No matter which subset of variables other than BT are held to their values in u and no matter how we set BT, we have SH = 1 and thus BS = 1.
in that case is {BT}, and it works under those definitions.) But now it is also easy to check that BT = 1 is not a cause of BS = 1 according to the modified HP definition. No matter which subset of variables other than BT are held to their values in u and no matter how we set BT, we have SH = 1 and thus BS = 1.
I did not completely specify ![[image]](images/dcleq0341.jpg) in the example above. Specifically, I did not specify the set of possible contexts. What happens in other contexts is irrelevant for determining whether ST = 1 or BT = 1 is a cause of BS = 1 in
in the example above. Specifically, I did not specify the set of possible contexts. What happens in other contexts is irrelevant for determining whether ST = 1 or BT = 1 is a cause of BS = 1 in ![[image]](images/dcleq0342.jpg) . But once I take normality considerations into account in Chapter 3, it will become relevant. I described u above as the context where Billy and Suzy both throw, implicitly suggesting that there are four contexts, determining the four possible combinations of Billy throwing and Suzy throwing. So we can take
. But once I take normality considerations into account in Chapter 3, it will become relevant. I described u above as the context where Billy and Suzy both throw, implicitly suggesting that there are four contexts, determining the four possible combinations of Billy throwing and Suzy throwing. So we can take ![[image]](images/dcleq0343.jpg) to be the model with these four contexts.
to be the model with these four contexts.
There is arguably a problem with this definition of ![[image]](images/dcleq0344.jpg) : it “bakes in” the temporal ordering of events, in particular, that Suzy’s rock hits before Billy’s rock. If we want a model that describes “rock-throwing situations for Billy and Suzy” more generally, we would not want to necessarily assume that Billy and Suzy are accurate, nor that Suzy always hits before Billy if they both throw. Whatever assumptions we make along these lines can be captured by the context. That is, we can have the context determine (a) whether Suzy and Billy throw, (b) how accurate they are (would Billy hit if he were the only one to throw, and similarly for Suzy), and (c) whose rock hits first if they both throw and are accurate (allowing for the possibility that they both hit at the same time). This richer model would thus have 48 contexts: there are four choices of which subset of Billy and Suzy throw, four possibilities for accuracy (both are accurate, Suzy is accurate and Billy is not, and so on), and three choices regarding who hits first if they both throw. If we use this richer model, we would also want to expand the language to include variables such as SA (Suzy is accurate), BA (Billy is accurate), SF (Suzy’s throw arrives first if both Billy and Suzy throw), and BF (Bily’s throw arrives first). Call this richer model
: it “bakes in” the temporal ordering of events, in particular, that Suzy’s rock hits before Billy’s rock. If we want a model that describes “rock-throwing situations for Billy and Suzy” more generally, we would not want to necessarily assume that Billy and Suzy are accurate, nor that Suzy always hits before Billy if they both throw. Whatever assumptions we make along these lines can be captured by the context. That is, we can have the context determine (a) whether Suzy and Billy throw, (b) how accurate they are (would Billy hit if he were the only one to throw, and similarly for Suzy), and (c) whose rock hits first if they both throw and are accurate (allowing for the possibility that they both hit at the same time). This richer model would thus have 48 contexts: there are four choices of which subset of Billy and Suzy throw, four possibilities for accuracy (both are accurate, Suzy is accurate and Billy is not, and so on), and three choices regarding who hits first if they both throw. If we use this richer model, we would also want to expand the language to include variables such as SA (Suzy is accurate), BA (Billy is accurate), SF (Suzy’s throw arrives first if both Billy and Suzy throw), and BF (Bily’s throw arrives first). Call this richer model ![[image]](images/dcleq0345.jpg) . In
. In ![[image]](images/dcleq0346.jpg) , the values of ST, BT, SA, BA, SF, and BF are determined by the context. As with
, the values of ST, BT, SA, BA, SF, and BF are determined by the context. As with ![[image]](images/dcleq0347.jpg) and
and ![[image]](images/dcleq0348.jpg) , the bottle shatters if either Suzy or Billy hit it, so we have the equation BS = BH ∨ SH. But now the equations for BH and SH depend on ST, BT, SA, BA, SF, and BF. Of course SH = 0 if Suzy doesn’t throw (i.e., if ST = 0) or is inaccurate (SA = 0), but even in this case, the equations need to tell us what would have happened had Suzy thrown and been accurate, so that we can determine the truth of formulas such as [ST ← 1, SA ← 1](SH = 0). As suggested by the discussion above, the equation for SH is
, the bottle shatters if either Suzy or Billy hit it, so we have the equation BS = BH ∨ SH. But now the equations for BH and SH depend on ST, BT, SA, BA, SF, and BF. Of course SH = 0 if Suzy doesn’t throw (i.e., if ST = 0) or is inaccurate (SA = 0), but even in this case, the equations need to tell us what would have happened had Suzy thrown and been accurate, so that we can determine the truth of formulas such as [ST ← 1, SA ← 1](SH = 0). As suggested by the discussion above, the equation for SH is
![[image]](images/dcleq0349.jpg)
In words, Suzy hits the bottle if she throws and is accurate, and either (a) Billy doesn’t throw, (b) Billy is inaccurate, or (c) Billy throws and is accurate but Suzy’s rock arrives at the bottle first (or at the same time as Billy’s); otherwise, Suzy doesn’t hit the bottle.
The context u in ![[image]](images/dcleq0350.jpg) corresponds to the context u∗ in
corresponds to the context u∗ in ![[image]](images/dcleq0351.jpg) where Billy and Suzy both throw, both are accurate, and Suzy’s throw hits first. Exactly the same argument as that above hows that ST = 1 is a cause of
where Billy and Suzy both throw, both are accurate, and Suzy’s throw hits first. Exactly the same argument as that above hows that ST = 1 is a cause of ![[image]](images/dcleq0352.jpg) , and BT = 1 is not. In the model
, and BT = 1 is not. In the model ![[image]](images/dcleq0353.jpg) , the direction of the edge in the causal network between SH and BH depends on the context. In some contexts (the ones where both Suzy and Billy are accurate and Suzy would hit first if they both throw), BH depends on SH; in other contexts, SH depends on BH. As a result,
, the direction of the edge in the causal network between SH and BH depends on the context. In some contexts (the ones where both Suzy and Billy are accurate and Suzy would hit first if they both throw), BH depends on SH; in other contexts, SH depends on BH. As a result, ![[image]](images/dcleq0354.jpg) is not what I called a strongly recursive model.
is not what I called a strongly recursive model. ![[image]](images/dcleq0355.jpg) is still a recursive model because in each context u′ in
is still a recursive model because in each context u′ in ![[image]](images/dcleq0356.jpg) , there are no cyclic dependencies; there is still an ordering
, there are no cyclic dependencies; there is still an ordering ![[image]](images/dcleq0357.jpg) on the endogenous variables such that unless
on the endogenous variables such that unless ![[image]](images/dcleq0358.jpg) , Y is independent of X in
, Y is independent of X in ![[image]](images/dcleq0359.jpg) . In particular, although
. In particular, although ![[image]](images/dcleq0360.jpg) and there is a context u″ in
and there is a context u″ in ![[image]](images/dcleq0361.jpg) such that
such that ![[image]](images/dcleq0362.jpg) ,
, ![[image]](images/dcleq0363.jpg) is still considered recursive.
is still considered recursive.
It is critical in this analysis of the rock-throwing example that the model includes the variables BH and SH, that is, that Billy’s rock hitting the bottle is taken to be a different event than Suzy’s rock hitting the bottle (although there is no problem if it includes extra variables). To understand the need for BH and SH (or some analogous variables), consider an observer watching the situation. Why would she declare Suzy’s throw to be a cause and Billy’s throw not to be a cause? Presumably, precisely because it was Suzy’s rock that hit the bottle and not Billy’s. If this is the reason for the declaration, then it must be modeled. Of course, using the variables BH and SH is not the only way of doing this. All that is needed is that the language be rich enough to allow us to distinguish the situation where Suzy’s rock hits and Billy’s rock does not from the one where Billy’s rock hits and Suzy’s rock does not. (That is why I said “or some analogous variables” above.) An alternative approach to incorporating temporal information is to have time-indexed variables (e.g., to have a family of variables BS k for “bottle shatters at time k” and a family Hk for “bottle is hit at time k”). With these variables and the appropriate equations, we can dispense with SH and BH and just have the variables H1, H2, … that talk about the bottle being hit at time k, without the variable specifying who hit the bottle. For example, if we assume that all the action happens at times 1, 2, and 3, then the equations are H1 = ST (if Suzy throws, then the bottle is hit at time 1), H2 = BT ∧¬H1 (the bottle is hit at time 2 if Billy throws and the bottle was not already hit at time 1), and BS = H1 ∨ H2 (if the bottle is hit, then it shatters). Again, these equations model the fact that Suzy hits first if she throws. And again, we could assume that the equations for H1 and H2 are context-dependent, so that Suzy hits first in u, but Billy hits first in u′. In any case, in context u where Suzy and Billy both throw but Suzy’s rock arrives at the bottle first, Suzy is still the cause, and Billy isn’t, using essentially the same analysis as that above.
To summarize the key point here, the language (i.e., the variables chosen and the equations for them) must be rich enough to capture the significant features of the story, but there is more than one language that can do this. As we shall see in Chapter 4, the choice of language can in general have a major impact on causality judgments. ■
The rock-throwing example emphasizes an important moral. If we want to argue in a case of preemption that X = x rather than Y = y is the cause of φ, then there must be a variable (BH in this case) that takes on different values depending on whether X = x or Y = y is the actual cause. If the model does not contain such a variable, then it will not be possible to determine which one is in fact the cause. The need for such variables is certainly consistent with intuition and the way we present evidence. If we want to argue (say, in a court of law) that it was A’s shot that killed C and not B’s, then, assuming that A shot from C’s left and B from the right, we would present evidence such as the bullet entering C from the left side. The side from which the shot entered is the relevant variable in this case. The variable may involve temporal evidence (if C’s shot had been the lethal one, then the death would have occurred a few seconds later), but it certainly does not have to.
The rock-throwing example also emphasizes the critical role of what happens in the actual situation in the definition. Specifically, we make use of the fact that, in the actual context, Billy’s rock did not hit the bottle. In the original and updated HP definition, this fact is applied in AC2(b): to show that Billy is a cause, we would have to show that the bottle shatters when Billy throws, even if BH is set to its actual value of 0. In the modified HP definition, it is applied in AC2(am) to show that Suzy’s throw is a cause: we can set ST = 0 while keeping BH fixed at 0. The analogous argument would not work to show that Billy’s throw is a cause.
Although what happens in the actual context certainly affects people’s causality judgments, why is the way that this is captured in AC2(am), AC2(bo), or AC2(bu) the “right” way of capturing it? I do not have a compelling answer to this question, beyond showing that these definitions work well in examples. I have tried to choose examples that, although not always realistic, capture important features of causality. For example, while the rock-throwing example may not seem so important in and of itself, it is an abstraction of a situation that arises frequently in legal cases, where one potential cause is preempted by another. Monopolistic practices by a big company cause a small company to go bankrupt, but it would have gone bankrupt anyway because of poor management; a smoker dies in a car accident, but he would have died soon due to inoperable lung cancer had there not been an accident. A good definition of causality is critical for teasing out what is a cause and what is not in such cases. Many of the other examples in this section are also intended to capture the essence of other important issues that arise in legal (and everyday) reasoning. It is thus worth understanding in all these cases exactly what the role of the actual context is.
Example 2.3.4 This example considers the problem of what has been called double prevention.
Suzy and Billy have grown up just in time to get involved in World War III. Suzy is piloting a bomber on a mission to blow up an enemy target, and Billy is piloting a fighter as her lone escort. Along comes an enemy fighter plane, piloted by Enemy. Sharp-eyed Billy spots Enemy, zooms in, and pulls the trigger; Enemy’s plane goes down in flames. Suzy’s mission is undisturbed, and the bombing takes place as planned.
Is Billy a cause of the success of the mission? After all, he prevented Enemy from preventing Suzy from carrying out the mission. Intuitively, it seems that the answer is yes, and the obvious causal model gives us this. Suppose that we have the following variables:
The causal network corresponding to this model is given in Figure 2.4.
In this model, BPT = 1 is a but-for cause of TD = 1, as is SBT = 1, so both BPT = 1 and SBT = 1 are causes of TD = 1 according to all the variants of the HP definition.
![[image]](images/fig2-4.jpg)
Figure 2.4: Blowing up the target.
We can make the story more complicated by adding a second fighter plane escorting Suzy, piloted by Hillary. Billy still shoots down Enemy, but if he hadn’t, Hillary would have. The natural way of dealing with this is to add just one more variable HPT representing Hillary’s pulling the trigger iff EE = 1 (see Figure 2.5), but then, using the naive but-for criterion, one might conclude that the target will be destroyed (TD = 1) regardless of Billy’s action, so BPT = 1 would not be a cause of TD = 1. All three variants of the HP definition still declare BPT = 1 to be a cause of TD = 1, as expected. We now take ![[image]](images/dcleq0364.jpg) and fix HPT at its value in the actual context, namely, 0. Although Billy’s action seems superfluous under ideal conditions, it becomes essential under a contingency where Hillary for some reason fails to pull the trigger. This contingency is represented by fixing HPT at 0 irrespective of EE.
and fix HPT at its value in the actual context, namely, 0. Although Billy’s action seems superfluous under ideal conditions, it becomes essential under a contingency where Hillary for some reason fails to pull the trigger. This contingency is represented by fixing HPT at 0 irrespective of EE.
![[image]](images/fig2-5.jpg)
Figure 2.5: Blowing up the target, with Billy and Hillary.
So far, this may all seem reasonable. But now go back to the original story and suppose that, again, Billy goes up along with Suzy, but Enemy does not actually show up. Is Billy going up a cause of the target being destroyed? Clearly, if Enemy had shown up, then Billy would have shot him down, and he would have been a but-for cause of the target being destroyed. But what about the context where Enemy does not show up? It seems that the original and updated HP definition would say that, even in that context, Billy going up is a cause of the target being destroyed. For if we consider the contingency where Enemy had shown up, then the target would not have been destroyed if Billy weren’t there, but since he is, the target is destroyed.
This may seem disconcerting. Suppose it is known that just about all the enemy’s aircraft have been destroyed, and no one has been coming up for days. Is Billy going up still a cause? The concern is that, if so, almost any A can become a cause of any B by telling a story of how there might have been a C that, but for A, would have prevented B from happening (just as there might have been an Enemy that prevented the target being destroyed had Billy not been there).
Does the HP definition really declare Billy showing up a cause of the target being destroyed in this case? Let’s look a little more carefully at how we model this story. If we want to call Billy going up a cause, then we need to add to the model a variable BGU corresponding to Billy going up. Similarly, we should add a variable ESU corresponding to Enemy showing up. We have the obvious equations, which say that (in the contexts of interest) BPT = 1 (i.e., Billy pulls the trigger) only if Billy goes up and Enemy shows up, and EE = 0 only if either Enemy doesn’t show up or Billy pulls the trigger. This gives us the model shown in Figure 2.6.
![[image]](images/fig2-6.jpg)
Figure 2.6: Blowing up the target, where Enemy may not show up.
In the actual world, where Billy goes up and Enemy doesn’t, Billy doesn’t pull the trigger (why should he?), so BPT = 0. Now it is easy to see that Billy going up (i.e., BGU = 1) is not a cause of the target being destroyed if Enemy doesn’t show up. AC2(bo) fails (and hence so does AC2(bu)): if Enemy shows up, the target won’t be destroyed, even if Billy shows up, because in the actual world BPT = 0. The modified HP definition addresses the problem even more straightforwardly. No matter which variables we fix to their actual values, TD = 1 even if BGU = 0. ■
Cases of prevention and double prevention are quite standard in the real world. It is standard to install fire alarms, which, of course, are intended to prevent fires. When the batteries in a fire alarm become weak, fire alarms typically “chirp”. Deactivating the chirping sound could be a cause of a fire not being detected due to double prevention: deactivating the chirping sound prevents the fire alarm from sounding, which in turn prevents the fire from being detected.
Example 2.3.5 Can not performing an action be (part of) a cause? Consider the following story.
Billy, having stayed out in the cold too long throwing rocks, contracts a serious but nonfatal disease. He is hospitalized and treated on Monday, so is fine Tuesday morning.
But now suppose that the doctor does not treat Billy on Monday. Is the doctor’s not treating Billy a cause of Billy’s being sick on Tuesday? It seems that it should be, and indeed it is according to all variants of the HP definition. Suppose that ![[image]](images/dcleq0365.jpg) is the context where, among other things, Billy is sick on Monday and the doctor forgets to administer the medication Monday. It seems reasonable that the model should have two variables:
is the context where, among other things, Billy is sick on Monday and the doctor forgets to administer the medication Monday. It seems reasonable that the model should have two variables:
Sure enough, in the obvious causal setting, MT = 0 is a but-for cause of BMC = 1, and hence a cause according to all three variants of the HP definition.
This may seem somewhat disconcerting at first. Suppose there are 100 doctors in the hospital. Although only one of them was assigned to Billy (and he forgot to give medication), in principle, any of the other 99 doctors could have given Billy his medication. Is the fact that they didn’t give him the medication also part of the cause of him still being sick on Tuesday?
In the causal model above, the other doctors’ failure to give Billy his medication is not a cause, since the model has no variables to model the other doctors’ actions, just as there was no variable in the causal model of Example 2.3.1 to model the presence of oxygen. Their lack of action is part of the context. We factor it out because (quite reasonably) we want to focus on the actions of Billy’s doctor.
If we had included endogenous variables corresponding to the other doctors, then they too would be causes of Billy’s being sick on Tuesday. The more refined definition of causality given in Chapter 3, which takes normality into account, provides a way of avoiding this problem even if the model includes endogenous variables for the other doctors. ■
Causation by omission is a major issue in the law. To take just one of many examples, a surgeon can be sued for the harm caused due to a surgical sponge that he did not remove after an operation.
The next example again emphasizes how the choice of model can change what counts as a cause.
Example 2.3.6 The engineer is standing by a switch in the railroad tracks. A train approaches in the distance. She flips the switch, so that the train travels down the right track instead of the left. Because the tracks reconverge up ahead, the train arrives at its destination all the same.
If we model this story using three variables—F for “flip”, with values 0 (the engineer doesn’t flip the switch) and 1 (she does); T for “track”, with values 0 (the train goes on the left track) and 1 (it goes on the right track); and A for “arrival”, with values 0 (the train does not arrive at the point of reconvergence) and 1 (it does)—then all three definitions agree that flipping the switch is not a cause of the train arriving.
But now suppose that we replace T with two binary variables, LB (for left track blocked), which is 0 if the left track is not blocked, and 1 if it is, and RB (for right track blocked), defined symmetrically. Suppose that LB, RB, and F are determined by the context, while the value of A is determined in the obvious way by which track the train is going down (which is determined by how the switch is set) and whether the track that it is going down is blocked; specifically, A = (F ∧¬LB) ∨ (¬F ∧ ¬RB). In the actual context, F = 1 and LB = RB = 0. Under the original and updated HP definition, F = 1 is a cause of A = 1. For in the contingency where LB = 1, if F = 1, then the train arrives, whereas if F = 0, then the train does not arrive. While adding the variables LB and RB suggests that we care about whether a track is blocked, it seems strange to call flipping the switch a cause of the train arriving when in fact both tracks are unblocked. This problem can be dealt with to some extent by invoking normality considerations, but not completely (see Example 3.4.3). With the modified definition, the problem disappears. Flipping the switch is not a cause of the train arriving if both tracks are unblocked, nor is it a cause of the train not arriving if both tracks are blocked. ■
Example 2.3.7 Suppose that a captain and a sergeant stand before a private, both shout “Charge!” at the same time, and the private charges. Some have argued that, because orders from higher-ranking officers trump those of lower-ranking officers, the captain is a cause of the charge, whereas the sergeant is not.
It turns out that which of the sergeant or captain is a cause depends in part on the variant of the HP definition we consider and in part on what the possible actions of the sergeant and captain are. First, suppose that the sergeant and the captain can each either order an advance, order a retreat, or do nothing. Formally, let C and S represent the captain’s and sergeant’s order, respectively. Then C and S can each take three values, 1, −1, or 0, depending on the order (attack, retreat, no order). The actual value of C and S is determined by the context. P describes what the private does; as the story suggests, P = C if C ≠ 0; otherwise P = S. In the actual context, C = S = P = 1.
C = 1 is a but-for cause of P = 1; setting C to −1 would result in P = −1. Thus, C = 1 is a cause of P = 1 according to all variants of the HP definition. S = 1 is not a cause of B = 1 according to the modified HP definition; changing S to 0 while keeping C fixed at 1 will not affect the private’s action. However, S = 1 is a cause of P = 1 according to the original and updated HP definition, with witness ({C}, 0, 0) (i.e., in the witness world, C = 0 and S = 0): if the captain does nothing, then what the private does is completely determined by the sergeant’s action.
Next, suppose that the captain and sergeant can only order an attack or a retreat; that is, the range of each of C and S is {−1, 1}. Now it is easy to check that C = 1 is the only cause of P = 1 according to all the variants of the HP definition. For the original and updated definition, S = 1 is not a cause because there is no setting of C that will allow the sergeant’s action to make a difference.
Finally, suppose that the captain and sergeant can only order an attack or do nothing; that is, the range of each of C and S is {0, 1}. C = 1 and S = 1 are both causes of P = 1 according to the original and updated HP definition, using the same argument used to show that S = 1 was a cause when it was also possible to order a retreat. Neither is a cause according to the modified HP definition, but C = 1 ∧ S = 1 is a cause, so both C = 1 and S = 1 are parts of a cause.
Note that if the range of the variables C and S is {0, 1}, then there is no way to capture the fact that in the case of conflicting orders, the private obeys the captain. In this setting, we can capture the fact that the private is “really” obeying the captain if both the captain and sergeant give orders by adding a new variable SE that captures the sergeant’s “effective” order. If the captain does not issue any orders (i.e., if C = 0), then SE = S. If the captain does issue an order, then SE = 0; the sergeant’s order is effectively blocked. In this model, P = C if C ≠ 0; otherwise, P = SE. The causal network for this model is given in Figure 2.7.
![[image]](images/fig2-7.jpg)
Figure 2.7: A model of commands that captures trumping.
In this model, the captain causes the private to advance, but the sergeant does not, according to all variants of the HP definition. To see that the captain is a cause according to the modified HP definition, hold SE fixed at 0 and set C = 0; clearly P = 0. By Theorem 2.2.3, C = 1 is a cause of P = 1 according to the original and updated definition as well. To show that S = 1 is not (part of) a cause according to all variants of the HP definition, it suffices to show it is not a cause according to the original HP definition. Suppose that we want to argue that S = 1 causes P = 1. The obvious thing to do is to take ![[image]](images/dcleq0366.jpg) and
and ![[image]](images/dcleq0367.jpg) . However, this choice does not satisfy AC2(bo): if C = 0, SE = 0 (its original value), and S = 1, then P = 0, not 1. The key point is that this more refined model allows a setting where C = 0, S = 1, and P = 0 (because SE = 0). That is, despite the sergeant issuing an order to attack and the captain being silent, the private does nothing. ■
. However, this choice does not satisfy AC2(bo): if C = 0, SE = 0 (its original value), and S = 1, then P = 0, not 1. The key point is that this more refined model allows a setting where C = 0, S = 1, and P = 0 (because SE = 0). That is, despite the sergeant issuing an order to attack and the captain being silent, the private does nothing. ■
The final example in this section touches on issues of responsibility in the law.
Example 2.3.8 Suppose that two companies both dump pollutant into the river. Company A dumps 100 kilograms of pollutant; company B dumps 60 kilograms. The fish in the river die. Biologists determine that k kilograms of pollutant suffice for the fish to die. Which company is the cause of the fish dying if k = 120, if k = 80, and if k = 50?
It is easy to see that if k = 120, then both companies are causes of the fish dying, according to all three definitions (each company is a but-for cause of the outcome). If k = 50, then each company is still a cause according to the original and updated HP definition. For example, to see that company B is a cause, we consider the contingency where company A does not dump any pollutant. Then the fish die if company B pollutes, but they survive if B does not pollute. With the modified definition, neither company individually is a cause; there is no variable that we can hold at its actual value that would make company A or company B a but-for cause. However, both companies together are the cause.
The situation gets more interesting if k = 80. Now the modified definition says that only A is a cause; if A dumps 100 tons of pollutant, then what B does has no impact. The original and updated definition also agree that A is a cause if k = 80. Whether B is a cause depends on the possible amounts of pollutant that A can dump. If A can dump only 0 or 100 kilograms of pollutant, then B is not a cause; no setting of A’s action can result in B’s action making a difference. However, if A can dump some amount between 20 and 79 kilograms, then B is a cause.
It’s not clear what the “right” answer should be here if k = 80. The law typically wants to declare B a contributing cause to the death of the fish (in addition to A), but should this depend on the amount of pollutant that A can dump? As we shall see in Section 6.2, thinking in terms of responsibility and blame helps clarify the issue (see Example 6.2.5). Under minimal assumptions about how likely various amounts of pollutant are to be dumped, B will get some degree of blame according to the modified definition, even when it is not a cause. ■
Example 2.4.1 Now consider the following modification of Example 2.3.5.
Suppose that Monday’s doctor is reliable and administers the medicine first thing in the morning, so that Billy is fully recovered by Tuesday afternoon. Tuesday’s doctor is also reliable and would have treated Billy if Monday’s doctor had failed to. … And let us add a twist: one dose of medication is harmless, but two doses are lethal.
Is the fact that Tuesday’s doctor did not treat Billy the cause of him being alive (and recovered) on Wednesday morning?
The causal model MB for this story is straightforward. There are three variables:
We can then describe Billy’s condition as a function of the four possible combinations of treatment/nontreatment on Monday and Tuesday. I omit the obvious structural equations corresponding to this discussion; the causal network is shown in Figure 2.8.
![[image]](images/fig2-8.jpg)
Figure 2.8: Billy’s medical condition.
In the context where Billy is sick and Monday’s doctor treats him, MT = 1 is a but-for cause of BMC = 0; if Billy had not been treated on Monday, then Billy would not have felt fine on Tuesday. MT = 1 is also a but-for cause of TT = 0, and TT = 0 is a but-for cause of Billy’s being alive (BMC ≠ 3, or equivalently, BMC = 0 ∨ BMC = 1 ∨ BMC = 2). However, MT = 1 is not part of a cause of Billy’s being alive, according to any variant of the HP definition. It suffices to show that it is not a cause according the original HP definition. This follows because setting MT = 0 cannot result in Billy dying, not matter how we fix TT.
This shows that causality is not transitive according to the HP definition. Although MT = 1 is a cause of TT = 0 and TT = 0 is a cause of BMC = 0 ∨ BMC = 1 ∨ BMC = 2, MT = 1 is not a cause of BMC = 0 ∨ BMC = 1 ∨ BMC = 2. Nor is causality closed under right weakening; that is, replacing a conclusion by something it implies. If A is a cause of B and B logically implies B′, then A may not be a cause of B′. In this case, MT = 1 is a cause of BMC = 0, which logically implies BMC = 0 ∨ BMC = 1 ∨ BMC = 2, which is not caused by MT = 1. ■
Although this example may seem somewhat forced, there are many quite realistic examples of lack of transitivity with exactly the same structure. Consider the body’s homeostatic system. An increase in external temperature causes a short-term increase in core body temperature, which in turn causes the homeostatic system to kick in and return the body to normal core body temperature shortly thereafter. But if we say that the increase in external temperature happened at time 0 and the return to normal core body temperature happened at time 1, we certainly would not want to say that the increase in external temperature at time 0 caused the body temperature to be normal at time 1!
There is another reason that causality is intransitive, which is illustrated by the following example.
Example 2.4.2 Suppose that a dog bites Jim’s right hand. Jim was planning to detonate a bomb, which he normally would do by pressing the button with his right forefinger. Because of the dog bite, he presses the button with his left forefinger. The bomb still goes off.
Consider the causal model with variables DB (the dog bites, with values 0 and 1), P (the press of the button, with values 0, 1, and 2, depending on whether the button is not pressed at all, pressed with the right hand, or pressed with the left hand), and B (the bomb goes off). We have the obvious equations: DB is determined by the context, P = DB + 1, and B = 1 if P is either 1 or 2. In the context where DB = 1, it is clear that DB = 1 is a but-for cause of P = 2 (if the dog had not bitten, P would have been 1), and P = 2 is a but-for cause of B = 1 (if P were 0, then B woud be 0), but DB = 1 is not a cause of P = 1. Regardless of whether the dog had bitten Jim, the button would have been pressed, and the bomb would have detonated. ■
In retrospect, the failure of right weakening is not so surprising. Taking true to be a tautology, if A is a cause of B, then we do not want to say that A is a cause of true, although B logically implies true. However, the failure of transitivity is quite surprising. Indeed, despite Examples 2.4.1 and 2.4.2, it seems natural to think of causality as transitive. People often think in terms of causal chains: A caused B, B caused C, C caused D, and therefore A caused D, where transitivity seems natural (although the law does not treat causality as transitive in long causal chains; see Section 3.4.4). Not surprisingly, there are some definitions of causality that require causality to be transitive; see the notes at the end of the chapter for details.
Why do we feel that causality is transitive? I believe that this is because, in typical settings, causality is indeed transitive. I give below two simple sets of conditions that are sufficient to guarantee transitivity. Because I expect that these conditions apply in many cases, it may explain why we naturally generalize to thinking of causality as transitive and are surprised when it is not.
For the purposes of this section, I restrict attention to but-for causes. This is what the law has focused on and seems to be the situation that arises most often in practice (although I will admit I have only anecdotal evidence to support this); certainly the law has done reasonably well by considering only but-for causality. Restricting to but-for causality has the further advantage that all the variants of the HP definition agree on what counts as a cause. (Thus, in this section, I do not specify which variant of the definition I am considering.) Restricting to but-for causality does not solve the transitivity problem. As Examples 2.4.1 and 2.4.2 already show, even if X1 = x1 is a but-for cause of X2 = x2 and X2 = x2 is a but-for cause of X3 = x3, it may not be the case that X1 = x1 is a cause of X3 = x3.
The first set of conditions assumes that X1, X2, and X3 each has a default setting. Such default settings make sense in many applications; “nothing happens” can be often taken as the default. Suppose, for example, a billiards expert hits ball A, causing it to hit ball B, causing it to carom into ball C, which then drops into the pocket. In this case, we can take the default setting for the shot to be the expert doing nothing and the default setting for the balls to be that they are not in motion. Let the default setting be denoted by the value 0.
Proposition 2.4.3 Suppose that
(a)X1 = x1 is a but-for cause of X2 = x2 in ![[image]](images/dcleq0368.jpg) ,
,
(b)X2 = x2 is a but-for cause of X3 = x3 in ![[image]](images/dcleq0369.jpg) ,
,
(c)x3 ≠ 0,
(d)![[image]](images/dcleq0370.jpg) , and
, and
(e)![[image]](images/dcleq0371.jpg) .
.
Then X1 = x1 is a but-for cause of X3 = x3 in ![[image]](images/dcleq0372.jpg) .
.
Proof: If X2 = 0 in the unique solution to the equations in the causal model ![[image]](images/dcleq0373.jpg) in context
in context ![[image]](images/dcleq0374.jpg) and X3 = 0 in the unique solution to the equations in
and X3 = 0 in the unique solution to the equations in ![[image]](images/dcleq0375.jpg) in context
in context ![[image]](images/dcleq0376.jpg) , then it is immediate that X3 = 0 in the unique solution to the equations in
, then it is immediate that X3 = 0 in the unique solution to the equations in ![[image]](images/dcleq0377.jpg) in context
in context ![[image]](images/dcleq0378.jpg) . That is,
. That is, ![[image]](images/dcleq0379.jpg) . It follows from assumption (a) that
. It follows from assumption (a) that ![[image]](images/dcleq0380.jpg) . We must thus have x1 ≠ 0; otherwise,
. We must thus have x1 ≠ 0; otherwise, ![[image]](images/dcleq0381.jpg) , so
, so ![[image]](images/dcleq0382.jpg) , which contradicts assumptions (b) and (c). Thus, X1 = x1 is a but-for cause of X3 = x3, since the value of X3 depends counterfactually on that of X1. ■
, which contradicts assumptions (b) and (c). Thus, X1 = x1 is a but-for cause of X3 = x3, since the value of X3 depends counterfactually on that of X1. ■
Although the conditions of Proposition 2.4.3 are clearly rather specialized, they arise often in practice. Conditions (d) and (e) say that if X1 remains in its default state, then so will X2, and if both X1 and X2 remain in their default states, then so will X3. Put another way, this says that the reason for X2 not being in its default state is X1 not being in its default state, and the reason for X3 not being in its default state is X1 and X2 both not being in their default states. The billiard example can be viewed as a paradigmatic example of when these conditions apply. It seems reasonable to assume that if the expert does not shoot, then ball A does not move; and if the expert does not shoot and ball A does not move (in the context of interest), then ball B does not move, and so on.![[image]](images/dcleq0383.jpg)
Of course, the conditions on Proposition 2.4.3 do not apply in either Example 2.4.1 or Example 2.4.2. The obvious default values in Example 2.4.1 are MT = TT = 0, but the equations say that in all contexts ![[image]](images/dcleq0384.jpg) of the causal model MB for this example, we have
of the causal model MB for this example, we have ![[image]](images/dcleq0385.jpg) . In the second example, if we take DB = 0 and P = 0 to be the default values of DB and P, then in all contexts
. In the second example, if we take DB = 0 and P = 0 to be the default values of DB and P, then in all contexts ![[image]](images/dcleq0386.jpg) of the causal model MD, we have
of the causal model MD, we have ![[image]](images/dcleq0387.jpg) .
.
While Proposition 2.4.3 is useful, there are many examples where there is no obvious default value. When considering the body’s homeostatic system, even if there is arguably a default value for core body temperature, what is the default value for the external temperature? But it turns out that the key ideas of the proof of Proposition 2.4.3 apply even if there is no default value. Suppose that X1 = x1 is a but-for cause of X2 = x2 in ![[image]](images/dcleq0388.jpg) and X2 = x2 is a but-for cause of X3 = x3 in
and X2 = x2 is a but-for cause of X3 = x3 in ![[image]](images/dcleq0389.jpg) . Then to get transitivity, it suffices to find values
. Then to get transitivity, it suffices to find values ![[image]](images/dcleq0390.jpg) ,
, ![[image]](images/dcleq0391.jpg) , and
, and ![[image]](images/dcleq0392.jpg) such that
such that ![[image]](images/dcleq0393.jpg) ,
, ![[image]](images/dcleq0394.jpg) , and
, and ![[image]](images/dcleq0395.jpg) . The argument in the proof of Proposition 2.4.3 (formalized in Lemma 2.10.2) shows that
. The argument in the proof of Proposition 2.4.3 (formalized in Lemma 2.10.2) shows that ![[image]](images/dcleq0396.jpg) . It then follows that X1 = x1 is a but-for cause of X3 = x3 in
. It then follows that X1 = x1 is a but-for cause of X3 = x3 in ![[image]](images/dcleq0397.jpg) . In Proposition 2.4.3,
. In Proposition 2.4.3, ![[image]](images/dcleq0398.jpg) ,
, ![[image]](images/dcleq0399.jpg) , and
, and ![[image]](images/dcleq0400.jpg) were all 0, but there is nothing special about the fact that 0 is a default value here. As long as we can find some values
were all 0, but there is nothing special about the fact that 0 is a default value here. As long as we can find some values ![[image]](images/dcleq0401.jpg) ,
, ![[image]](images/dcleq0402.jpg) , and
, and ![[image]](images/dcleq0403.jpg) , these conditions apply. I formalize this as Proposition 2.4.4, which is a straightforward generalization of Proposition 2.4.3.
, these conditions apply. I formalize this as Proposition 2.4.4, which is a straightforward generalization of Proposition 2.4.3.
Proposition 2.4.4 Suppose that there exist values ![[image]](images/dcleq0404.jpg) ,
, ![[image]](images/dcleq0405.jpg) , and
, and ![[image]](images/dcleq0406.jpg) such that
such that
(a)X1 = x1 is a but-for cause of X2 = x2 in ![[image]](images/dcleq0407.jpg) ,
,
(b)X2 = x2 is a but-for cause of X3 = x3 in ![[image]](images/dcleq0408.jpg) ,
,
(c)![[image]](images/dcleq0409.jpg) ,
,
(d)![[image]](images/dcleq0410.jpg) (i.e.,
(i.e., ![[image]](images/dcleq0411.jpg) ), and
), and
(e)![[image]](images/dcleq0412.jpg) (i.e.,
(i.e., ![[image]](images/dcleq0413.jpg) ).
).
Then X1 = x1 is a but-for cause of X3 = x3 in ![[image]](images/dcleq0414.jpg) .
.
To see how these ideas apply, suppose that a student receives an A+ in a course, which causes her to be accepted at Cornell University (her top choice, of course!), which in turn causes her to move to Ithaca. Further suppose that if she had received an A in the course, she would have gone to university U1 and as a result moved to city C1, and if she had gotten anything else, she would have gone to university at U2 and moved to city C2. This story can be captured by a causal model with three variables: G for her grade, U for the university she goes to, and C for the city she moves to. There are no obvious default values for any of these three variables. Nevertheless, we have transitivity here: The student’s A+ was a cause of her being accepted at Cornell, and being accepted at Cornell was a cause of her move to Ithaca; it seems like a reasonable conclusion that the student’s A+ was a cause of her move to Ithaca. Indeed, transitivity follows from Proposition 2.4.4. We can take the student getting an A to be ![[image]](images/dcleq0415.jpg) , the student being accepted at university U1 to be
, the student being accepted at university U1 to be ![[image]](images/dcleq0416.jpg) , and the student moving to C1 to be
, and the student moving to C1 to be ![[image]](images/dcleq0417.jpg) (assuming that U1 is not Cornell and that C1 is not Ithaca, of course).
(assuming that U1 is not Cornell and that C1 is not Ithaca, of course).
The conditions provided in Proposition 2.4.4 are not only sufficient for causality to be transitive, they are necessary as well, as the following result shows.
Proposition 2.4.5 If X1 = x1 is a but-for cause of X3 = x3 in ![[image]](images/dcleq0418.jpg) , then there exist values
, then there exist values ![[image]](images/dcleq0419.jpg) ,
, ![[image]](images/dcleq0420.jpg) , and
, and ![[image]](images/dcleq0421.jpg) such that
such that ![[image]](images/dcleq0422.jpg) ,
, ![[image]](images/dcleq0423.jpg) , and
, and ![[image]](images/dcleq0424.jpg) .
.
Proof: Since X1 = x1 is a but-for cause of X3 = x3 in ![[image]](images/dcleq0425.jpg) , there must exist a value
, there must exist a value ![[image]](images/dcleq0426.jpg) such that
such that ![[image]](images/dcleq0427.jpg) . Let
. Let ![[image]](images/dcleq0428.jpg) and
and ![[image]](images/dcleq0429.jpg) be such that
be such that ![[image]](images/dcleq0430.jpg) . It easily follows that
. It easily follows that ![[image]](images/dcleq0431.jpg) . ■
. ■
In light of Propositions 2.4.4 and 2.4.5, understanding why causality is so often taken to be transitive comes down to finding sufficient conditions to guarantee the assumptions of Proposition 2.4.4. I now present a set of conditions sufficient to guarantee the assumptions of Proposition 2.4.4, motivated by the two examples showing that causality is not transitive. To deal with the problem in Example 2.4.2, I require that for every value ![[image]](images/dcleq0432.jpg) in the range of X2, there is a value
in the range of X2, there is a value ![[image]](images/dcleq0433.jpg) in the range of X1 such that
in the range of X1 such that ![[image]](images/dcleq0434.jpg) . This requirement holds in many cases of interest; it is guaranteed to hold if X1 = x1 is a but-for cause of X2 = x2 and X2 is binary (since but-for causality requires that two different values of X1 result in different values of X2). But this requirement does not hold in Example 2.4.2; no setting of DB can force P to be 0.
. This requirement holds in many cases of interest; it is guaranteed to hold if X1 = x1 is a but-for cause of X2 = x2 and X2 is binary (since but-for causality requires that two different values of X1 result in different values of X2). But this requirement does not hold in Example 2.4.2; no setting of DB can force P to be 0.
Imposing this requirement still does not deal with the problem in Example 2.4.1. To do that, we need one more condition: X2 must lie on every causal path from X1 to X3. Roughly speaking, this says that all the influence of X1 on X3 goes through X2. This condition does not hold in Example 2.4.1: as Figure 2.8 shows, there is a direct causal path from MT to BMC that does not include TT. However, this condition does hold in many cases of interest. Going back to the example of the student’s grade, the only way that the student’s grade can influence which city the student moves to is via the university that accepts the student.
To make this precise, I first need to define causal path. A causal path in a causal setting ![[image]](images/dcleq0435.jpg) is a sequence (Y1, …, Yk) of variables such that Yj+1 depends on Yj in context
is a sequence (Y1, …, Yk) of variables such that Yj+1 depends on Yj in context ![[image]](images/dcleq0436.jpg) for j = 1, …, k − 1. Since there is an edge between Yj and Yj+1 in the causal network for M (assuming that we fix context
for j = 1, …, k − 1. Since there is an edge between Yj and Yj+1 in the causal network for M (assuming that we fix context ![[image]](images/dcleq0437.jpg) ) exactly if Yj+1 depends on Yj, a causal path is just a path in the causal network. A causal path in
) exactly if Yj+1 depends on Yj, a causal path is just a path in the causal network. A causal path in ![[image]](images/dcleq0438.jpg) from X1 to X2 is just a causal path whose first node is X1 and whose last node is X2. Finally, Y lies on a causal path in
from X1 to X2 is just a causal path whose first node is X1 and whose last node is X2. Finally, Y lies on a causal path in ![[image]](images/dcleq0439.jpg) from X1 to X2 if Y is a node (possibly X1 or X2) on a causal path in
from X1 to X2 if Y is a node (possibly X1 or X2) on a causal path in ![[image]](images/dcleq0440.jpg) from X1 to X2.
from X1 to X2.
The following result summarizes the second set of conditions sufficient for transitivity. (Recall that ![[image]](images/dcleq0441.jpg) denotes the range of the variable X.)
denotes the range of the variable X.)
Proposition 2.4.6 Suppose that X1 = x1 is a but-for cause of X2 = x2 in the causal setting ![[image]](images/dcleq0442.jpg) , X2 = x2 is a but-for cause of X3 = x3 in
, X2 = x2 is a but-for cause of X3 = x3 in ![[image]](images/dcleq0443.jpg) , and the following two conditions hold:
, and the following two conditions hold:
(a)for every value ![[image]](images/dcleq0444.jpg) , there exists a value
, there exists a value ![[image]](images/dcleq0445.jpg) such that
such that ![[image]](images/dcleq0446.jpg) ;
;
(b)X2 is on every causal path in ![[image]](images/dcleq0447.jpg) from X1 to X3.
from X1 to X3.
Then X1 = x1 is a but-for cause of X3 = x3.
The proof of Proposition 2.4.6 is not hard, although we must be careful to get all the details right. The high-level idea of the proof is easy to explain. Suppose that X2 = x2 is a but-for cause of X3 = x3 in ![[image]](images/dcleq0448.jpg) . Then there must be some values
. Then there must be some values ![[image]](images/dcleq0450.jpg) and
and ![[image]](images/dcleq0451.jpg) such that
such that ![[image]](images/dcleq0452.jpg) . By assumption, there exists a value
. By assumption, there exists a value ![[image]](images/dcleq0453.jpg) such that
such that ![[image]](images/dcleq0454.jpg) . The requirement that X2 is on every causal path from X1 to X3 guarantees that
. The requirement that X2 is on every causal path from X1 to X3 guarantees that ![[image]](images/dcleq0455.jpg) implies
implies ![[image]](images/dcleq0456.jpg) in
in ![[image]](images/dcleq0457.jpg) (i.e.,
(i.e., ![[image]](images/dcleq0458.jpg) implies
implies ![[image]](images/dcleq0459.jpg) ). Roughly speaking, X2 “screens off” the effect of X1 on X3, since it is on every causal path from X1 to X3. Now we can apply Proposition 2.4.4. I defer the formal argument to Section 2.10.2.
). Roughly speaking, X2 “screens off” the effect of X1 on X3, since it is on every causal path from X1 to X3. Now we can apply Proposition 2.4.4. I defer the formal argument to Section 2.10.2.
It is easy to construct examples showing that the conditions of Proposition 2.4.6 are not necessary for causality to be transitive. Suppose that X1 = x1 causes X2 = x2, X2 = x2 causes X3 = x3, and there are several causal paths from X1 to X3. Roughly speaking, the reason that X1 = x1 may not be a but-for cause of X3 = x3 is that the effects of X1 on X3 may “cancel out” along the various causal paths. This is what happens in the homeostasis example. If X2 is on all the causal paths from X1 to X3, then as we have seen, all the effect of X1 on X3 is mediated by X2, so the effect of X1 on X3 on different causal paths cannot “cancel out”. But even if X2 is not on all the causal paths from X1 to X3, the effects of X1 on X3 may not cancel out along the causal paths, and X1 = x1 may still be a cause of X3 = x3. That said, it seems difficult to find a weakening of the condition in Proposition 2.4.6 that is simple to state and suffices for causality to be transitive.
In general, an agent trying to determine whether A is a cause of B may not know the exact model or context. An agent may be uncertain about whether Suzy and Billy both threw, or just Suzy threw; he may be uncertain about who will hit first if both Suzy and Billy throw (or perhaps they hit simultaneously). In a perhaps more interesting setting, at some point, people were uncertain about whether smoking caused cancer or whether smoking and cancer were both the outcome of the same genetic problem, which would lead to smoking and cancer being correlated, but no causal relationship between the two. To deal with such uncertainty, an agent can put a probability on causal settings. For each causal setting ![[image]](images/dcleq0460.jpg) , the agent can determine whether A is a cause of B in
, the agent can determine whether A is a cause of B in ![[image]](images/dcleq0461.jpg) , and so compute the probability that A is a cause of B. Having probabilities on causal settings will be relevant in the discussion of blame in Chapter 6. Here I focus on what seems to be a different source of uncertainty: uncertainty in the equations. In causal models, all the equations are assumed to be deterministic. However, as was observed, in many cases, it seems more reasonable to think of outcomes as probabilistic. So rather than thinking of Suzy’s rock as definitely hitting the bottle if she throws, we can think of her as hitting with probability .9. That is, rather than taking Suzy to always be accurate, we can take her to be accurate with some probability.
, and so compute the probability that A is a cause of B. Having probabilities on causal settings will be relevant in the discussion of blame in Chapter 6. Here I focus on what seems to be a different source of uncertainty: uncertainty in the equations. In causal models, all the equations are assumed to be deterministic. However, as was observed, in many cases, it seems more reasonable to think of outcomes as probabilistic. So rather than thinking of Suzy’s rock as definitely hitting the bottle if she throws, we can think of her as hitting with probability .9. That is, rather than taking Suzy to always be accurate, we can take her to be accurate with some probability.
The first step in considering how to define causality in the presence of uncertain outcomes is to show how this uncertainty can be captured in the formal framework. Earlier, I assumed that, for each endogenous variable X, there was a deterministic function FX that described the value of X as a function of all the other variables. Now, rather than assuming that FX returns a particular value, I assume that it returns a distribution over the values of X given the values of all other variables. This is perhaps easiest to understand by means of an example. In the rock-throwing example, rather than assuming that if Suzy throws a rock, she definitely hits the bottle, suppose we assume that she only only hits it with probability .9 and misses with probability .1. Suppose that if Billy throws and Suzy hasn’t hit the bottle, then Billy will hit it with probability.8 and miss with probability .2. Finally, for simplicity, assume that, if hit by either Billy or Suzy, the bottle will definitely shatter.
The next two paragraphs show how the probabilistic version of this story can be modeled formally in the structural-equations framework and can be skipped on a first reading. Recall that for the more sophisticated model ![[image]](images/dcleq0462.jpg) of the (deterministic) rock-throwing story, although I earlier wrote the equation for SH as SH = ST, this is really an abbreviation for the function FSH (i1, i2, i3, i4, i5) = i2: FSH is a function of the values of the exogenous variable U (which is not described in the causal network but determines the values of BT and ST) and the endogenous variables ST, BT, BH, and BS. These values are given by i1, …, i5. The equation SH = ST says that the value of SH depends only on the value of ST and is equal to it; that explains the output i2. For the probabilistic version of the story, FSH (i1, 1, i3, i4, i5) is the probability distribution that places probability .9 on the value 1 and probability .1 on the value 0. In words, this says that if Suzy throws (ST = 1), then no matter what the values i1, i3, i4, and i5 of U, BT, BH, and BS are, respectively, FSH (i1, 1, i3, i4, i5) is the probability distribution that puts probability .9 on the event SH = 1 and probability .1 on the event SH = 0. This captures the fact that if Suzy throws, then she has a probability .9 of hitting the bottle (no matter what Billy does). Similarly, FSH (i1, 0, i3, i4, i5) is the distribution that places probability 1 on the value 0: if Suzy doesn’t throw, then she certainly won’t hit the bottle, so the event SH = 0 has probability 1.
of the (deterministic) rock-throwing story, although I earlier wrote the equation for SH as SH = ST, this is really an abbreviation for the function FSH (i1, i2, i3, i4, i5) = i2: FSH is a function of the values of the exogenous variable U (which is not described in the causal network but determines the values of BT and ST) and the endogenous variables ST, BT, BH, and BS. These values are given by i1, …, i5. The equation SH = ST says that the value of SH depends only on the value of ST and is equal to it; that explains the output i2. For the probabilistic version of the story, FSH (i1, 1, i3, i4, i5) is the probability distribution that places probability .9 on the value 1 and probability .1 on the value 0. In words, this says that if Suzy throws (ST = 1), then no matter what the values i1, i3, i4, and i5 of U, BT, BH, and BS are, respectively, FSH (i1, 1, i3, i4, i5) is the probability distribution that puts probability .9 on the event SH = 1 and probability .1 on the event SH = 0. This captures the fact that if Suzy throws, then she has a probability .9 of hitting the bottle (no matter what Billy does). Similarly, FSH (i1, 0, i3, i4, i5) is the distribution that places probability 1 on the value 0: if Suzy doesn’t throw, then she certainly won’t hit the bottle, so the event SH = 0 has probability 1.
Similarly, in the deterministic model of the rock-throwing example, The function FBH is such that FBH (i1, i2, i3, i4, i5) = 1 if (i3, i4) = (1, 0), and is 0 otherwise. That is, taking i1, …, i5 to be the values of U, ST, BT, SH, and BS, respectively, Billy’s throw hits the bottle only if he throws (i3 = 1) and Suzy doesn’t hit the bottle (i4 = 0). For the probabilistic version of the story, FBH (i1, i2, i3, i4, i5) is the distribution that puts probability .8 on 1 and probability .2 on 0; for all other values of i3 and i4, FBH (i1, i2, 1, 0, i5) puts probability 1 on 0. (Henceforth, I just describe the probabilities in words rather than using the formal notation.)
The interpretation of these probabilities is similar to the interpretation of the deterministic equations we have used up to now. For example, the fact that Suzy’s rock hits with probability.9 does not mean that the probability of Suzy’s rock hitting conditional on her throwing is .9; rather, it means that if there is an intervention that results in Suzy throwing, the probability of her hitting is .9. The probability of rain conditional on a low barometer reading is high. However, intervening on the barometer reading, say, by setting the needle to point to a low reading, does not affect the probability of rain.
There have been many attempts to give a definition of causality that takes probability into account. They typically take A to be a cause of B if A raises the probability of B. I am going to take a different approach here. I take a standard technique in computer science to “pull out the probability”, allowing me to convert a single causal setting where the equations are probabilistic to a probability over causal settings, where in each causal setting, the equations are deterministic. This, in turn, will allow me to avoid giving a separate definition of probabilistic causality. Rather, I will be able to use the definition of causality already given for deterministic models and talk about the probability of causality, that is, the probability that A is a cause of B. As we shall see, this approach seems to deal naturally with a number of problems regarding probabilistic causality that have been raised in the literature.
The assumption is that the equations would be deterministic if we knew all the relevant details. This assumption is probably false at the quantum level; most physicists believe that at this level, the world is genuinely probabilistic. But for the macroscopic events that I focus on in this book (and that most people are interested in when applying causality judgments), it seems reasonable to view the world as fundamentally deterministic. With this viewpoint, if Suzy hits the rock with probability .9, then there must be (perhaps poorly understood) reasons that cause her to miss: an unexpected gust of wind or a momentary distraction throwing off her aim. We can “package up” all these factors and make them exogenous. That is, we can have an exogenous variable U′ with values either 0 or 1 depending on whether the features that cause Suzy to miss are present, where U′ = 0 with probability .1 and U′ = 1 with probability .9. By introducing such a variable U′ (and a corresponding variable for Billy), we have essentially pulled the probability out of the equations and put it into the exogenous variable.
I now show in more detail how this approach plays out in the context of the rock-throwing example with the probabilities given above. Consider the causal setting where Suzy and Billy both throw. We may be interested in knowing the probability that Suzy or Billy will be a cause of the bottle shattering if we don’t know whether the bottle will in fact shatter, or in knowing the probability that Suzy or Billy is the cause if we know that the bottle actually did shatter. (Notice that in the former case, we are asking about an effect of a (possible) cause, whereas in the latter case, we are asking about the cause of an effect.) When we pull out the probability, there are four causal models that arise here, depending on whether Suzy’s rock hits the bottle and whether Billy’s rock hits the bottle if Suzy’s rock does not hit. Specifically, consider the following four models, in a context where both Suzy and Billy throw rocks:
Note that these models differ in their structural equations, although they involve the same exogenous and endogenous variables. M1 is just the model considered earlier, described in Figure 2.3. Suzy’s throw is a cause in M1 and M2; Billy’s throw is a cause in M3.
If we know that the bottle shattered, Suzy’s rock hit, and Billy’s didn’t, then the probability that Suzy is the cause is 1. We are conditioning on the model being either M1 or M2 because these are the models where Suzy’s rock hits, and Suzy is the cause of the bottle shattering in both. But suppose that all we know is that the bottle shattered, and we are trying to determine the probability that Suzy is the cause. Now we can condition on the model being either M1, M2, or M3, so if the prior probability of M4 is p, then the probability that Suzy is a cause of the bottle shattering is .9/(1 − p): Suzy is a cause of the bottle shattering as long as she hits the bottle and it shatters (i.e., in models M1 and M2). Unfortunately, the story does not give us that the probability of M4. It is .1 − q, where q is the prior probability of M3, but the story does not tell us that either. We can say more if we make a reasonable additional assumption: that whether Suzy’s rock hits is independent of whether Billy’s rock would hit if Suzy missed. Then M1 has probability .72 (= .9 × .8), M2 has probability .18, M3 has probability .08, and M4 has probability .02. With this assumption and no further information, the probability of Suzy being a cause of the bottle shatter is .9/.98 = 45/49.
Although it seems reasonable to view the outcomes “Suzy’s rock hits the bottle” and “Billy’s rock would have hit the bottle if Suzy’s hadn’t” as independent, they certainly do not have to be. We could, for example, assume that Billy and Suzy are perfectly accurate when there are no wind gusts and miss when there are wind gusts, and that wind gusts occur with probability .7. Then it would be the case that Suzy’s rock hits with probability .7 and that Billy’s rock would have hit with probability .7 if Suzy’s had missed, but there would have been only two causal models: the one that we considered in the deterministic case, which would be the actual model with probability .7, and the one where both miss. (A better model of this situation might have an exogenous variable U′ such that U′ = 1 if there are wind gusts and U′ = 0 if there aren’t, and then have deterministic equations for SH and BH.) The key message here is that, in general, further information might be needed to determine the probability of causality beyond what is provided by probabilistic structural equations as defined above.
A few more examples should help illustrate how this approach works and how much we can say.
Example 2.5.1 Suppose that a doctor treats Billy on Monday. The treatment will result in Billy recovering on Tuesday with probability .9. But Billy might also recover with no treatment due to some other factors, with independent probability .1. By “independent probability” here, I mean that conditional on Billy being treated on Monday, the events “Billy recovers due to the treatment” and “Billy recovers due to other factors” are independent; thus, the probability that Billy will not recover on Tuesday given that he is treated on Monday is (.1)(.9). Now, in fact, Billy is treated on Monday and he recovers on Tuesday. Is the treatment the cause of Billy getting better?
The standard answer is yes, because the treatment greatly increases the likelihood of Billy getting better. But there is still the nagging concern that Billy’s recovery was not due to the treatment. He might have gotten better if he had just been left alone.
Formally, we have a causal model with three endogenous binary variables: MT (the doctor treats Billy on Monday), OF (the other factors that would make Billy get better occur), and BMC (Billy’s medical condition, which we can take to be 1 if he gets better and 0 otherwise). The exogenous variable(s) determine MT and OF. The probability that MT = 1 does not matter for this analysis; for definiteness, assume that MT = 1 with probability .8. According to the story, OF = 1 with probability .9. Finally, BMC = 1 if OF = 1, BMC = 0 if MT = OF = 0, and BMC = 1 with probability .9 if MT = 1 and OF = 0. Again, after we pull out the probability, there are eight models, which differ in whether MT is set to 0 or 1, whether OF is set to 0 or 1, and whether BMC = 1 when MT = 1 and OF = 0. Treating these choices as independent (as is suggested by the story), it is straightforward to calculate the probability of each of the eight models. Since we know that Billy actually did get better and was treated by his doctor, we ignore the four models where MT = 0 and the model where MT = 1, OF = 0, and BMC = 0 if MT = 1 and OF = 0. The remaining three models have probability .8(1 − (.9)(.1)). MT = 1 is a cause of BMC = 0 in two of the three models; it is not a cause only in the model where OF = 1, MT = 1, but BMC would be 0 if OF were set to 0. This latter model has prior probability .8(.1)(.1). Straightforward calculations now show that the treatment cause of Billy’s recovery with probability ![[image]](images/dcleq0463.jpg) . Similarly, the probability that Billy’s recovery was caused by other factors is
. Similarly, the probability that Billy’s recovery was caused by other factors is ![[image]](images/dcleq0464.jpg) . These probabilities sum to more than 1 because with probability
. These probabilities sum to more than 1 because with probability ![[image]](images/dcleq0465.jpg) , both are causes; Billy’s recovery is overdetermined.
, both are causes; Billy’s recovery is overdetermined.
Now suppose that we can perform a (somewhat expensive) test to determine whether the doctor’s treatment actually caused Billy to get better. Again, the doctor treats Billy and Billy recovers, but the test is carried out, and it is shown that the treatment was not the cause. It is still the case that the treatment significantly raises the probability of Billy recovering, but now we certainly don’t want to call the treatment the cause. And, indeed, it is not. Conditioning on the information, we can discard three of the four models. The only one left is the one in which Billy’s recovery is due to other factors (with probability 1). Moreover, this conclusion does not depend on the independence assumption. ■
Example 2.5.2 Now suppose that there is another doctor who can treat Billy on Monday, with different medication. Both treatments are individually effective with probability .9. Unfortunately, if Billy gets both treatments and both are effective, then, with probability.8, there will be a bad interaction, and Billy will die. For this version of the story, suppose that there are no other factors involved; if Billy gets neither treatment, he will not recover. Further suppose that we can perform a test to see whether a treatment was effective. Suppose that in fact both doctors treat Billy and, despite that, Billy recovers on Tuesday. Without further information, there are three relevant models: in the first, only the first doctor’s medication was effective; in the second, only the second doctor’s medication was effective; in the third, both are effective. If further testing shows that both treatments were effective, then there is no uncertainty; we are down to just one model: the third one. According to the original and updated HP definition, both treatments are the cause of Billy’s recovery, with probability 1. (According to the modified HP definition, they are both parts of the cause.) This is true despite the fact that, given that the first doctor treated Billy, the second doctor treating Billy significantly lowers the probability of Billy recovering (and symmetrically with the roles of the doctors reversed). ■
Example 2.5.3 Now suppose that a doctor has treated 1,000 patients. They each would have had probability .9 of recovering even without the treatment. With the treatment, they recover with independent probability .1 In fact, 908 patients recovered, and Billy is one of them. What is the probability that the treatment was the cause of Billy’s recovery? Calculations similar to those in Example 2.5.1 show that it is 10/91. Standard probabilistic calculations show that there is quite a high probability that the treatment is a cause of at least one patient’s recovery. Indeed, there is quite a high probability that the treatment is the unique cause of at least one patient’s recovery. But we do not know which patient that is. ■
Example 2.5.4 Again, Billy and Suzy throw rocks at a bottle. If either Billy or Suzy throws a rock, it will hit the bottle. But now the bottle is heavy and will, in general, not topple over if it is hit. If only Billy hits the bottle, it will topple over with probability.2; similarly, if only Suzy hits the bottle, it will topple over with probability.2. If they hit the bottle simultaneously, it will topple with probability.7. In fact, both Billy and Suzy throw rocks at the bottle, and it topples over. We are interested in the extent to which Suzy and Billy are the causes of the bottle toppling over.
For simplicity, I restrict attention to contexts where both Billy and Suzy throw, both hit, and the bottle topples over. After pulling out the probability, there are four causal models of interest, depending on what would have happened if just Suzy had hit the bottle and if just Billy had hit the bottle:
I further simplify by treating the outcomes “the bottle would have toppled over had only Suzy’s rock hit it” and “the bottle would have toppled over had only Billy’s rock hit it” as independent (even though neither may be independent of the outcome “the bottle would have toppled over had both Billy and Suzy’s rocks hit it”). With this assumption, the probability of M1 (conditional on the bottle toppling over if both Suzy’s and Billy’s rock hit it) is .04, the conditional probability of M2 is .16, the conditional probability of M3 is .16, and the conditional probability of M4 is .64.
It is easy to check that Suzy’s throw is a cause of the bottle toppling in models M1, M2, and M4, but not in M3. Similarly, Billy’s throw is a cause in models M1, M3, and M4. They are both causes in models M1 and M4 according to the original and updated HP definition, as well as in M4 according to the modified HP definition; in M1, the conjunction ST = 1 ∧ BT = 1 is a cause according to the modified HP definition. Thus, the probability that Suzy’s throw is part of a cause of the bottle shattering is .84, and likewise for Billy. The probability that both are parts of causes is .68 (since this is the case in models M1 and M4). ■
As these examples show, the HP definition lets us make perfectly sensible statements about the probability of causality. There is nothing special about these examples; all other examples can be handled equally well. Perhaps the key message here is that there is no need to work hard on getting a definition of probabilistic causality, at least at the macroscopic level; it suffices to get a good definition of deterministic causality. But what about if we want to treat events at the quantum level, which seems inherently probabilistic? A case can still be made that it is psychologically useful to think deterministically. Whether the HP definitions can be extended successfully to an inherently probabilistic framework still remains open.
Even if we ignore issues at the microscopic level, there is still an important question to be addressed: In what sense is the single model with probabilistic equations equivalent to the set of deterministic causal models with a probability on them? In a naive sense, the answer is no. The examples above show that the probabilistic equations do not in general suffice to determine the probability of the deterministic causal models. Thus, there is a sense in which deterministic causal models with a probability on them carry more information than a single probabilistic model. Moreover, this extra information is useful. As we have seen, it may be necessary to determine the answer to questions such as “How probable is it that Billy is the cause of the bottle shattering?” when all we see is a shattered bottle and know that Billy and Suzy both threw. Such a determination can be quite important in, for example, legal cases. Although bottle shattering may not be of great legal interest, we may well want to know the probability of Bob being the cause of Charlie dying in a case where there are multiple potential causes.
If we make reasonable independence assumptions, then a probabilistic model determines a probability on deterministic models. Moreover, under the obvious assumptions regarding the semantics of causal models with probabilistic equations, formulas in the language described in Section 2.2.1 have the same probability of being true under both approaches. Consider Example 2.5.4 again. What is the probability of a formula like [ST ← 0](BS = 1) (if Suzy hadn’t thrown, the bottle would have shattered)? Clearly, of the four deterministic models described in the discussion of this example, the formula is true only in M1 and M3; thus, it has probability .2. Although I have not given a semantics for formulas in this language in probabilistic causal models (i.e., models where the equations are probabilistic), if we assume that the outcomes “the bottle would have toppled over had only Suzy’s rock hit it” and “the bottle would have toppled over had only Billy’s rock hit it” are independent, as I assumed when assigning probabilities to the deterministic models, we would expect this statement to also be true in the probabilistic model. The converse holds as well: if a statement about the probability of causality holds in the probabilistic model, then it holds in the corresponding deterministic model.
This means that (under the independence assumption) as far as the causal language of Section 2.2.1 is concerned, the two approaches are equivalent. Put another way, to distinguish the two approaches, we need a richer language. More generally, although we can debate whether pulling out the probability “really” gives an equivalent formulation of the situation, to the extent that the notion of (probabilistic) causality is expressible in the language of Section 2.2.1, the two approaches are equivalent. In this sense, it is safe to reduce to deterministic models.
This observation leads to two further points. Suppose that we do not want to make the relevant independence assumptions. Is there a natural way to augment probabilistic causal models to represent this information (beyond just going directly to a probability over deterministic causal models)? See Section 5.1 for further discussion of this point.
Of course, we do not have to use probability to represent uncertainty; other representations of uncertainty could be used as well. Indeed, there is a benefit to using a representation that involves sets of probabilities. Since, in general, probabilistic structural equations do not determine the probability of the deterministic models that arise when we pull out the probability, all we have is a set of possible probabilities on the deterministic models. Given that, it seems reasonable to start with sets of probabilities on the equations as well. This makes sense if, for example, we do not know the exact probability that Suzy’s rock would hit the bottle, but we know that it would hit it with probability between .6 and .8. It seems that the same general approach of pulling out the probabilities works if we represent uncertainty using sets of probabilities, but I have not explored this approach in detail.
Although counterfactual dependence is a key feature of causality, people’s causality judgments are clearly influenced by another quite different feature: how sensitive the causality ascription is to changes in various other factors. If we assume that Suzy is very accurate, then her throwing a rock is a robust cause of the bottle shattering. The bottle will shatter regardless of whether Billy throws, even if the bottle is in a slightly different position and even if it is slightly windy. On the other hand, suppose instead that we consider a long causal chain like the following: Suzy throws a rock at a lock, causing it to open, causing the lion that was in the locked cage to escape, frightening the cat, which leapt up on to the table and knocked over the bottle, which then shattered. Although Suzy’s throw is still a but-for cause of the bottle shattering, the shattering is clearly sensitive to many other factors. If Suzy’s throw had not broken the lock, if the lion had run in a different direction, or if the cat had not jumped on the table, then the bottle would not have shattered. People seem inclined to assign less blame to Suzy’s throw in this case. I return to the issue of long causal chains in Sections 3.4.4 and provide a solution to it using the notion of blame in Section 6.2. Here I define a notion of sufficient causality that captures some of the intuitions behind insensitive causation. Sufficient causality also turns out to be related to the notion of explanation that I define in Chapter 7, so it is worth considering in its own right, although it will not be a focus of this book.
The key intuition behind the definition of sufficient causality is that not only does ![[image]](images/dcleq0466.jpg) suffice to bring about φ in the actual context (which is the intuition that AC2(bo) and AC2(bu) are trying to capture), but it also brings it about in other “nearby” contexts. Since the framework does not provide a metric on contexts, there is no obvious way to define nearby context. Thus, in the formal definition below, I start by considering all contexts. Since conjunction plays a somewhat different role in this definition than it does in the definition of actual causality (particularly in the modified HP definition), I take seriously here the intuition that what we really care about are parts of causes, rather than causes.
suffice to bring about φ in the actual context (which is the intuition that AC2(bo) and AC2(bu) are trying to capture), but it also brings it about in other “nearby” contexts. Since the framework does not provide a metric on contexts, there is no obvious way to define nearby context. Thus, in the formal definition below, I start by considering all contexts. Since conjunction plays a somewhat different role in this definition than it does in the definition of actual causality (particularly in the modified HP definition), I take seriously here the intuition that what we really care about are parts of causes, rather than causes.
Again, there are three variants of the notion of sufficient causality, depending on which version of AC2 we use. The differences between these variants do not play a role in our discussion, so I just write AC2 below. Of course, if we want to distinguish, AC2 below can be replaced by either AC2(a) and AC2(bo), AC2(a) and AC2(bu), or AC2(am), depending on which version of the HP definition is being considered.
Definition 2.6.1 ![[image]](images/dcleq0467.jpg) is a sufficient cause of φ in the causal setting
is a sufficient cause of φ in the causal setting ![[image]](images/dcleq0468.jpg) if the following conditions hold:
if the following conditions hold:
SC1. ![[image]](images/dcleq0469.jpg) and
and ![[image]](images/dcleq0470.jpg) .
.
SC2. Some conjunct of ![[image]](images/dcleq0471.jpg) is part of a cause of φ in
is part of a cause of φ in ![[image]](images/dcleq0472.jpg) . More precisely, there exists a conjunct X = x of
. More precisely, there exists a conjunct X = x of ![[image]](images/dcleq0473.jpg) and another (possibly empty) conjunction
and another (possibly empty) conjunction ![[image]](images/dcleq0474.jpg) such that
such that ![[image]](images/dcleq0475.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dcleq0476.jpg) ; that is, AC1, AC2, and AC3 hold for
; that is, AC1, AC2, and AC3 hold for ![[image]](images/dcleq0477.jpg) .
.
SC3. ![[image]](images/dcleq0478.jpg) for all contexts
for all contexts ![[image]](images/dcleq0479.jpg) .
.
SC4. ![[image]](images/dcleq0480.jpg) is minimal; there is no strict subset
is minimal; there is no strict subset ![[image]](images/dcleq0481.jpg) of
of ![[image]](images/dcleq0482.jpg) such that
such that ![[image]](images/dcleq0483.jpg) satisfies conditions SC1, SC2, and SC3, where
satisfies conditions SC1, SC2, and SC3, where ![[image]](images/dcleq0484.jpg) is the restriction of
is the restriction of ![[image]](images/dcleq0485.jpg) to the variables in
to the variables in ![[image]](images/dcleq0486.jpg) . ■
. ■
SC3 is the key condition here; it says that ![[image]](images/dcleq0487.jpg) suffices to bring about φ in all contexts. Thus, in the case of the 11–0 victory, any set of six voters becomes a sufficient cause (no matter which variant of the HP definition we use), assuming that there are contexts corresponding to all possible voting configurations. This suggests that sufficient causality is related to the modified HP definition, which, in this case, would also take any subset of six voters to be a cause. However, this is misleading, as the next example shows.
suffices to bring about φ in all contexts. Thus, in the case of the 11–0 victory, any set of six voters becomes a sufficient cause (no matter which variant of the HP definition we use), assuming that there are contexts corresponding to all possible voting configurations. This suggests that sufficient causality is related to the modified HP definition, which, in this case, would also take any subset of six voters to be a cause. However, this is misleading, as the next example shows.
Consider the forest-fire example again. In the disjunctive model, each of L = 1 and MD = 1 is a sufficient cause; in the conjunctive model, L = 1 ∧ MD = 1 is a sufficient cause, assuming that there is a context where there is no lightning and another where the arsonist does not drop a match. This is the case for all variants of the HP definition. Recall that this is just the opposite of what the modified HP definition does with actual causality; it would declare L = 1 ∧ MD = 1 the cause in the disjunctive model and both L = 1 and MD = 1 individually causes in the conjunctive model.
I wrote SC2 as I did so as to take seriously the notion that all we really care about when using the modified (and updated) definition is parts of causes. Thus, in the disjunctive model for the forest fire example, L = 1 and MD = 1 are both sufficient causes of the forest fire in the context (1, 1) where there is both a lightning strike and a dropped match, even if we use AC2(am) in SC2. By assumption, SC3 holds: both [L ← 1](FF = 1) and [MD ← 1](FF = 1) hold in all contexts. Moreover, both L = 1 and MD = 1 are parts of a cause of FF = 1 (namely, L = 1 MD = 1), so SC2 holds.
The forest-fire example shows that sufficient causality lets us distinguish what can be called joint causes from independent causes. In the disjunctive forest-fire model, the lightning and the dropped match can each be viewed as independent causes of the fire; each suffices to bring it about. In the conjunctive model, the lightning and the dropped match are joint causes; their joint action is needed to bring about the forest fire. The distinction between joint and independent causality seems to be one that people are quite sensitive to. Not surprisingly, it plays a role in legal judgments.
Going on with examples, consider the sophisticated rock-throwing model ![[image]](images/dcleq0488.jpg) from Example 2.3.3 again. Assume that Suzy is always accurate; that is, she is accurate in all contexts where she throws, and would be accurate even in contexts where she doesn’t throw if (counterfactually) she were to throw; that is, assume that [ST ← 1](BS = 1) holds in all contexts, even if Suzy does not actually throw. Then Suzy’s throw is a sufficient cause of the bottle shattering in the context that we have been considering, where both Billy and Suzy throw, and Suzy’s throw actually hits the bottle. Billy’s throw is not a sufficient cause in this context because it is not even (part of) a cause. However, if we consider the model
from Example 2.3.3 again. Assume that Suzy is always accurate; that is, she is accurate in all contexts where she throws, and would be accurate even in contexts where she doesn’t throw if (counterfactually) she were to throw; that is, assume that [ST ← 1](BS = 1) holds in all contexts, even if Suzy does not actually throw. Then Suzy’s throw is a sufficient cause of the bottle shattering in the context that we have been considering, where both Billy and Suzy throw, and Suzy’s throw actually hits the bottle. Billy’s throw is not a sufficient cause in this context because it is not even (part of) a cause. However, if we consider the model ![[image]](images/dcleq0489.jpg) , which has a larger set of contexts, including ones where Suzy might throw and miss, then ST = 1 is not a sufficient cause of BS = 1 in the context u∗ where Suzy is accurate and her rock hits before Billy’s, but SH = 1 is. Recall that ST = 1 remains a cause of BS = 1 in
, which has a larger set of contexts, including ones where Suzy might throw and miss, then ST = 1 is not a sufficient cause of BS = 1 in the context u∗ where Suzy is accurate and her rock hits before Billy’s, but SH = 1 is. Recall that ST = 1 remains a cause of BS = 1 in ![[image]](images/dcleq0490.jpg) . This shows that (part of) a cause is not necessarily part of a sufficient cause.
. This shows that (part of) a cause is not necessarily part of a sufficient cause.
In the double-prevention example (Example 2.3.4), assuming that Suzy is accurate, SBT = 1 (Suzy bombing the target) is a sufficient cause of TD = 1 (the target being destroyed). In contrast, Billy pulling the trigger and shooting down Enemy is not, if there are contexts where Suzy does not go up, and thus does not destroy the target. More generally, a but-for cause at the beginning of a long causal chain is unlikely to be a sufficient cause.
The definition of actual causality (Definition 2.2.1) focuses on the actual context; the set of possible contexts plays no role. By way of contrast, the set of contexts plays a major role in the definition of sufficient causality. The use of SC3 makes sufficient causality quite sensitive to the choice of the set of possible contexts. It also may make it an unreasonably strong requirement in some cases. Do we want to require SC3 to hold even in some extremely unlikely contexts? A sensible way to weaken SC3 would be to add probability to the picture, especially if we have a probability on contexts, as in Section 2.5. Rather than requiring SC3 to hold for all contexts, we could then consider the probability of the set of contexts for which it holds. That is, we can take ![[image]](images/dcleq0491.jpg) to be a sufficient cause of φ with probability α in
to be a sufficient cause of φ with probability α in ![[image]](images/dcleq0492.jpg) if SC1, SC2, and SC4 hold and the set of contexts for which SC3 holds has probability at least α.
if SC1, SC2, and SC4 hold and the set of contexts for which SC3 holds has probability at least α.
Notice that with this change, there is a tradeoff between minimality and probability of sufficiency. Consider Suzy throwing rocks. Suppose that, although Suzy is quite accurate, there is a (quite unlikely) context where there are high winds, so Suzy misses the bottle. In this model, a sufficient cause for the bottle shattering is “Suzy throws and there are no high winds”. Suzy throwing is not by itself sufficient. But it is sufficient in all contexts but the one in which there are high winds. If the context with high winds has probability .1, then Suzy’s throw is a sufficient cause of the bottle shattering with probability .9.
This tradeoff between minimality and probability of sufficiency comes up again in the context of the definition of explanation, considered in Section 7.1, so I do not dwell on it here. But thinking in terms of probability provides some insight into whether not performing an action should be treated as a sufficient cause. Consider Example 2.3.5, where Billy is hospitalized. Besides Billy’s doctor, there are other doctors at the hospital who could, in principle, treat Billy. But they are unlikely to do so. Indeed, they will not even check up on Billy unless they are told to; they presumably have other priorities.
Now consider a context where in fact no doctor treats Billy. In that case, Billy’s doctor not treating Billy on Monday is a sufficient cause for Billy feeling sick on Tuesday with high probability because, with high probability, no other doctor would treat him either. However, another doctor not treating Billy has only a low probability of being a sufficient cause for Billy feeling sick on Tuesday because, with high probability, Billy’s doctor does treat him. This intuition is similar in spirit to the way normality considerations are brought to bear on this example in Chapter 3 (see Example 3.2.2).
For the most part, I do not focus on sufficient causality in this book. I think that notions such as normality, blame, and explanation capture many of the same intuitions as sufficient causality in an arguably better way. However, it is worth keeping sufficient causality in mind when we consider these other notions.
2.7 Causality in Nonrecursive Models
Up to now, I have considered causality only in recursive (i.e., acyclic) causal models. Recursive models are also my focus throughout the rest of the book. However, there are examples that arguably involve nonrecursive models. For example, the connection between pressure and volume is given by Boyle’s Law, which says that PV = k: the product of pressure and volume is a constant (if the temperature remains constant). Thus, increasing the pressure decreases the volume, and decreasing the volume increases the pressure. There is no direction of causality in this equation. However, in any particular setting, we are typically manipulating either the pressure or the volume, so there is (in that setting) a “direction” of causality.
Perhaps a more interesting example is one of collusion. Imagine two arsonists who agree to burn down the forest, when only one match suffices to burn down the forest. (So we are essentially in the disjunctive model.) However, the arsonists make it clear to each other that each will not drop a lighted match unless the other does. At the critical moment, they look in each others’ eyes, and both drop their lit matches, resulting in the forest burning down. In this setting, it is plausible that each arsonist caused the other to throw the match, and together they caused the forest to burn down. That is, if MDi stands for “arsonist i drops a lit match”, for i = 1, 2, and U is an exogenous variable that determines whether the arsonists initially intend to drop the match, we can take the equation for MD1 to be such that MD 1 = 1 if and only if U = 1 and MD2 = 1, and similarly for MD2. This model is not recursive; in all contexts, MD1 depends on MD 2 and MD 2 depends on MD1. In this section, I show how the HP definition(s) can be extended to deal with such nonrecursive models.
In nonrecursive models, there may be more than one solution to an equation in a given context, or there may be none. In particular, this means that a context no longer necessarily determines the values of the endogenous variables. Earlier, I identified a primitive event such as X = x with the basic causal formula [ ](X = x), that is, a formula of the form [Y1 ← y1, …, Yk ← yk](X = x) with k = 0. In recursive causal models, where there is a unique solution to the equations in a given context, we can define [ ](X = x) to be true in ![[image]](images/dcleq0493.jpg) if X = x is the unique solution to the equations in context
if X = x is the unique solution to the equations in context ![[image]](images/dcleq0494.jpg) . It seems reasonable to identify [ ](X = x) with X = x in this case. But it is not so reasonable if there may be several solutions to the equations or none.
. It seems reasonable to identify [ ](X = x) with X = x in this case. But it is not so reasonable if there may be several solutions to the equations or none.
What we really want to do is to be able to say that X = x under a particular setting of the variables. Thus, we now take the truth of a primitive event such as X = x to be relative not just to a context but to a complete assignment: a complete description ![[image]](images/dcleq0495.jpg) of the values of both the exogenous and the endogenous variables. As before, the context
of the values of both the exogenous and the endogenous variables. As before, the context ![[image]](images/dcleq0496.jpg) assigns a value to all the exogenous variables;
assigns a value to all the exogenous variables;![[image]](images/dcleq0497.jpg) assigns a value to all the endogenous variables. Now define
assigns a value to all the endogenous variables. Now define ![[image]](images/dcleq0498.jpg) if X has value x in
if X has value x in ![[image]](images/dcleq0499.jpg) . Since the truth of X = x depends on just
. Since the truth of X = x depends on just ![[image]](images/dcleq0500.jpg) , not
, not ![[image]](images/dcleq0501.jpg) , I sometimes write
, I sometimes write ![[image]](images/dcleq0502.jpg) .
.
This definition can be extended to Boolean combinations of primitive events in the standard way. Define ![[image]](images/dcleq0503.jpg) iff
iff ![[image]](images/dcleq0504.jpg) for all solutions
for all solutions ![[image]](images/dcleq0505.jpg) to the equations in
to the equations in ![[image]](images/dcleq0506.jpg) . Since the truth of
. Since the truth of ![[image]](images/dcleq0507.jpg) depends only on the setting
depends only on the setting ![[image]](images/dcleq0508.jpg) of the exogenous variables, and not on
of the exogenous variables, and not on ![[image]](images/dcleq0509.jpg) , I write
, I write ![[image]](images/dcleq0510.jpg) to emphasize this.
to emphasize this.
With these definitions in hand, it is easy to extend the HP definition of causality to arbitrary models. Causality is now defined with respect to a tuple ![[image]](images/dcleq0511.jpg) because we need to know the values of the endogenous variables to determine the truth of some formulas. That is, we now talk about
because we need to know the values of the endogenous variables to determine the truth of some formulas. That is, we now talk about ![[image]](images/dcleq0512.jpg) being an actual cause of φ in
being an actual cause of φ in ![[image]](images/dcleq0513.jpg) . As before, we have conditions AC1–AC3. AC1 and AC3 remain unchanged. AC2 depends on whether we want to consider the original, updated, or modified definition. For the updated definition, we have:
. As before, we have conditions AC1–AC3. AC1 and AC3 remain unchanged. AC2 depends on whether we want to consider the original, updated, or modified definition. For the updated definition, we have:
AC2. There exists a partition ![[image]](images/dcleq0514.jpg) of
of ![[image]](images/dcleq0515.jpg) with
with ![[image]](images/dcleq0516.jpg) and some setting
and some setting ![[image]](images/dcleq0517.jpg) of the variables in
of the variables in ![[image]](images/dcleq0518.jpg) such that
such that
(a)![[image]](images/dcleq0519.jpg) .
.
(bu)If ![[image]](images/dcleq0520.jpg) is such that
is such that ![[image]](images/dcleq0521.jpg) , then, for all subsets
, then, for all subsets ![[image]](images/dcleq0522.jpg) of
of ![[image]](images/dcleq0523.jpg) and
and ![[image]](images/dcleq0524.jpg) of
of ![[image]](images/dcleq0525.jpg) ,
, ![[image]](images/dcleq0526.jpg) .
.
In recursive models, the formula ![[image]](images/dcleq0527.jpg) in the version of AC2(a) above is equivalent to
in the version of AC2(a) above is equivalent to ![[image]](images/dcleq0528.jpg) , the formula used in the original formulation of AC2(a). Given a recursive model M, there is a unique solution to the equations in
, the formula used in the original formulation of AC2(a). Given a recursive model M, there is a unique solution to the equations in ![[image]](images/dcleq0529.jpg) ;
;![[image]](images/dcleq0530.jpg) holds in that solution iff φ does not hold. However, with nonrecursive models, there may several solutions; AC2(a) holds if φ does not hold in at least one of them. By way of contrast, for AC2(bu) to hold, φ must stay true in all solutions to the equations in
holds in that solution iff φ does not hold. However, with nonrecursive models, there may several solutions; AC2(a) holds if φ does not hold in at least one of them. By way of contrast, for AC2(bu) to hold, φ must stay true in all solutions to the equations in ![[image]](images/dcleq0531.jpg) in context
in context ![[image]](images/dcleq0532.jpg) . AC2(a) already says that there is some contingency in which setting
. AC2(a) already says that there is some contingency in which setting ![[image]](images/dcleq0533.jpg) to
to ![[image]](images/dcleq0534.jpg) is necessary to bring about φ (since setting
is necessary to bring about φ (since setting ![[image]](images/dcleq0535.jpg) to something other than
to something other than ![[image]](images/dcleq0536.jpg) in that contingency may result in φ no longer holding). Requiring ¬φ to hold in only one solution to the equations seems in the spirit of the necessity requirement. However, AC2(bu) says that setting
in that contingency may result in φ no longer holding). Requiring ¬φ to hold in only one solution to the equations seems in the spirit of the necessity requirement. However, AC2(bu) says that setting ![[image]](images/dcleq0537.jpg) to
to ![[image]](images/dcleq0538.jpg) is sufficient to bring about φ in all relevant settings, so it makes sense that we want φ to hold in all solutions. That’s part of the intuition for sufficiency. Clearly, in the recursive case, where there is only one solution, this definition agrees with the definition given earlier.
is sufficient to bring about φ in all relevant settings, so it makes sense that we want φ to hold in all solutions. That’s part of the intuition for sufficiency. Clearly, in the recursive case, where there is only one solution, this definition agrees with the definition given earlier.
Analogous changes are required to extend the original and modified HP definition to the nonrecursive case. For AC2(bo), we require only that for all subsets ![[image]](images/dcleq0539.jpg) of
of ![[image]](images/dcleq0540.jpg) , we have
, we have ![[image]](images/dcleq0541.jpg) , and do not require this to hold for all subsets
, and do not require this to hold for all subsets ![[image]](images/dcleq0542.jpg) of
of ![[image]](images/dcleq0543.jpg) ; for AC2(am), we require that
; for AC2(am), we require that ![[image]](images/dcleq0544.jpg) consist of the values of the variables in
consist of the values of the variables in ![[image]](images/dcleq0545.jpg) in the actual context. Again, these definitions agree with the earlier definitions in the recursive case.
in the actual context. Again, these definitions agree with the earlier definitions in the recursive case.
Note that, with these definitions, all definitions agree that MD1 = 1 and MD2 = 1 are causes of the fire in the collusive disjunctive scenario discussed above. This is perhaps most interesting in the case of the modified HP definition, where in the original disjunctive scenario, the cause was the conjunction MD = 1 ∧ L = 1. However, in this case, each arsonist is a but-for cause of the fire. Although it takes only one match to start the fire, if arsonist 1 does not drop his match, then arsonist 2 won’t drop his match either, so there will not be a fire. The key point is that the arsonists do not act independently here, whereas in the original story, the arsonist and lightning were viewed as independent.
Interestingly, we can make even the collusion story recursive. Suppose that we add a variable EC for eye contact (allowing for the possibility that the arsonists avoid each other’s eyes), where the equations are such that each drops the match only if they do indeed have eye contact. Now we are back at a model where each arsonist is (separately) a cause of the fire (as is the eye contact) according to the original and updated HP definition, and MD1 = 1 ∧ MD 2 = 1 is a cause according to the modified HP definition. We can debate which is the “better” model here. But I have no reason to believe that we can always replace a nonrecursive model by a recursive model and still describe essentially the same situation.
Finally, it is worth noting that causality is not necessarily asymmetric in nonrecursive models; we can have X = x being a cause of Y = y and Y = y being a cause of X = x. For example, in the model of the collusive story above (without the variable EC), MD1 = 1 is a cause of MD2 = 1 and MD2 = 1 is a cause of MD1 = 1. It should not be so surprising that we can have such symmetric causality relations in nonrecursive models. However, it is easy to see that causality is asymmetric in recursive models, according to all the variants of the HP definition. AC2(a) and AC2(am) guarantee that if X = x is a cause of Y = y in (M, u), then Y depends on X in context u. Similarly, X must depend on Y if Y = y is a cause of X = x in (M, u). This cannot be the case in a recursive model.
Although the definition of causality in nonrecursive models given here seems like the most natural generalization of the definition for recursive models, I do not have convincing examples suggesting that this is the “right” definition, nor do I have examples showing that this definition is problematic in some ways. This is because all the standard examples are most naturally modeled using recursive models. It would be useful to have more examples of scenarios that are best captured by nonrecursive models for which we have reasonable intuitions regarding the ascription of causality.
In this section, I consider more carefully AC2(bo) and AC2(bu), to give the reader a sense of the subtle differences between original and updated HP definition. I start with the example that originally motivated replacing AC2(bo) by AC2(bu).
Example 2.8.1 Suppose that a prisoner dies either if A loads B’s gun and B shoots or if C loads and shoots his gun. Taking D to represent the prisoner’s death and making the obvious assumptions about the meaning of the variables, we have that D = (A ∧ B) C. (Note that here I am identifying the binary variables A, B, C, and D with primitive propositions in propositional logic, as I said earlier I would. I could have also written this as D = max(min(A, B), C).) Suppose that in the actual context u, A loads B’s gun, B does not shoot, but C does load and shoot his gun, so the prisoner dies. That is, A = 1, B = 0, and C = 1. Clearly C = 1 is a cause of D = 1. We would not want to say that A = 1 is a cause of D = 1, given that B did not shoot (i.e., given that B = 0). However, suppose that we take the obvious model with the variables A, B, C, D. With AC2(bo), A = 1 is a cause of D = 1. For we can take ![[image]](images/dcleq0546.jpg) and consider the contingency where B = 1 and C = 0. It is easy to check that AC2(a) and AC2(bo) hold for this contingency, since (M, u) ⊨ [A ← 0, B ←1, C ← 0](D = 0), whereas (M, u) = [A ← 1, B ← 1, C ← 0](D = 1). Thus, according to the original HP definition, A = 1 is a cause of D = 1. However, AC2(bu) fails in this case because (M, u) ⊨ [A ← 1, C ← 0](D = 0). The key point is that AC2(bu) says that for A = 1 to be a cause of D = 1, it must be the case that D = 1 even if only some of the values in
and consider the contingency where B = 1 and C = 0. It is easy to check that AC2(a) and AC2(bo) hold for this contingency, since (M, u) ⊨ [A ← 0, B ←1, C ← 0](D = 0), whereas (M, u) = [A ← 1, B ← 1, C ← 0](D = 1). Thus, according to the original HP definition, A = 1 is a cause of D = 1. However, AC2(bu) fails in this case because (M, u) ⊨ [A ← 1, C ← 0](D = 0). The key point is that AC2(bu) says that for A = 1 to be a cause of D = 1, it must be the case that D = 1 even if only some of the values in ![[image]](images/dcleq0547.jpg) are set to their values
are set to their values ![[image]](images/dcleq0548.jpg) . In this case, by setting only A to 1 and leaving B unset, B takes on its original value of 0, in which case D = 0. AC2(bo) does not consider this case.
. In this case, by setting only A to 1 and leaving B unset, B takes on its original value of 0, in which case D = 0. AC2(bo) does not consider this case.
Note that the modified HP definition also does not call A = 1 a cause of D = 1. This follows from Theorem 2.2.3 and the observations above; it can also be seen easily by observing that if the values of any subset of variables are fixed at their actual values in context u, setting A = 0 will not make D = 0.
Although it seems clear that we do not want A = 1 to be a cause of D = 1, the situation for the original HP definition is not as bleak as it may appear. We can deal with this example using the original HP definition if we add extra variables, as we did with the Billy-Suzy rock-throwing example. Specifically, suppose that we add a variable B′ for “B shoots a loaded gun”, where B′ = A ∧ B and D = B′ ∨ C. This slight change prevents A = 1 from being a cause of D = 1, even according to the original HP definition. I leave it to the reader to check that any attempt to now declare A = 1 a cause of D = 1 according to the original HP definition would have to put B′ into ![[image]](images/dcleq0549.jpg) . However, because B′ = 0 in the actual world, AC2(bo) does not hold. As I show in Section 4.3, this approach to dealing with the problem generalizes. There is a sense in which, by adding enough extra variables, we can always use AC2(bo) instead of AC2(bu) to get equivalent judgments of causality. ■
. However, because B′ = 0 in the actual world, AC2(bo) does not hold. As I show in Section 4.3, this approach to dealing with the problem generalizes. There is a sense in which, by adding enough extra variables, we can always use AC2(bo) instead of AC2(bu) to get equivalent judgments of causality. ■
There are advantages to using AC2(bo). For one thing, it follows from Theorem 2.2.3(d) that with AC2(bo), causes are always single conjuncts. This is not the case with AC2(bu), as the following example shows.
Example 2.8.2 A votes for a candidate. A’s vote is recorded in two optical scanners B and C. D collects the output of the scanners; D′ records whether just scanner B records a vote for the candidate. The candidate wins (i.e., WIN = 1) if any of A, D, or D′ is 1. The value of A is determined by the exogenous variable. The following structural equations characterize the value of the remaining variables:
Call this causal model MV. Roughly speaking, D′ acts like BH in the rock-throwing example as modeled by ![[image]](images/dcleq0550.jpg) . The causal network for MV is shown in Figure 2.9.
. The causal network for MV is shown in Figure 2.9.
In the actual context u, A = 1, so B = C = D = WIN = 1 and D′ = 0. I claim that B = 1 ∧ C = 1 is a cause of WIN = 1 in (MV, u) according to the updated HP definition (which means that, by AC3, neither B = 1 nor C = 1 is cause of WIN = 1 in (MV, u)). To see this, first observe that AC1 clearly holds. For AC2, consider the witness where ![[image]](images/dcleq0551.jpg) (so
(so ![[image]](images/dcleq0552.jpg) ) and w = 0 (so we are considering the contingency where A = 0). Clearly, (MV, u) ⊨ [A ← 0, B ← 0, C ← 0](WIN = 0), so AC2(a) holds, and (MV, u) ⊨ [A ← 0, B ← 1, C ← 1](WIN = 1). Moreover, (MV, u) ⊨ [B ← 1, C ← 1](WIN = 1), and WIN = 1 continues to hold even if D is set to 1 and/or D′ is set to 0 (their values in (MV, u)). Thus, AC2 holds.
) and w = 0 (so we are considering the contingency where A = 0). Clearly, (MV, u) ⊨ [A ← 0, B ← 0, C ← 0](WIN = 0), so AC2(a) holds, and (MV, u) ⊨ [A ← 0, B ← 1, C ← 1](WIN = 1). Moreover, (MV, u) ⊨ [B ← 1, C ← 1](WIN = 1), and WIN = 1 continues to hold even if D is set to 1 and/or D′ is set to 0 (their values in (MV, u)). Thus, AC2 holds.
![[image]](images/fig2-9.jpg)
Figure 2.9: Another voting scenario.
It remains to show that AC3 holds and, in particular, that neither B = 1 nor C = 1 is a cause of WIN = 1 in (MV, u) according to the updated HP definition. The argument is essentially the same for both B = 1 and C = 1, so I just show it for B = 1. Roughly speaking, B = 1 does not satisfy AC2(a) and AC2(bu) for the same reason that BT = 1 does not satisfy it in the rock-throwing example. For suppose that B = 1 satisfies AC2(a) and AC2(bu). Then we would have to have ![[image]](images/dcleq0553.jpg) , and we would need to consider the contingency where A = 0 (otherwise WIN = 1 no matter how we set B). Now we need to consider two cases:
, and we would need to consider the contingency where A = 0 (otherwise WIN = 1 no matter how we set B). Now we need to consider two cases: ![[image]](images/dcleq0554.jpg) and
and ![[image]](images/dcleq0555.jpg) . If
. If ![[image]](images/dcleq0556.jpg) , then if we set D′ = 0, we have (MV, u) ⊨ [A ← 0, B ← 1, D′ ← 0](WIN = 0), so AC2(bu) fails (no matter whether C and D are in
, then if we set D′ = 0, we have (MV, u) ⊨ [A ← 0, B ← 1, D′ ← 0](WIN = 0), so AC2(bu) fails (no matter whether C and D are in ![[image]](images/dcleq0557.jpg) or
or ![[image]](images/dcleq0558.jpg) ). And if we set D′ = 1, then AC2(a) fails, since (MV, u) ⊨ [A ← 0, B ← 0, D′ ← 1](WIN = 1). Now if
). And if we set D′ = 1, then AC2(a) fails, since (MV, u) ⊨ [A ← 0, B ← 0, D′ ← 1](WIN = 1). Now if ![[image]](images/dcleq0559.jpg) , note that (MV, u) ⊨ D′ = 0. Since (MV, u) ⊨ [A ← 0, B ← 1, D′ ← 0](WIN = 0), again AC2(bu) fails (no matter whether C or D are in
, note that (MV, u) ⊨ D′ = 0. Since (MV, u) ⊨ [A ← 0, B ← 1, D′ ← 0](WIN = 0), again AC2(bu) fails (no matter whether C or D are in ![[image]](images/dcleq0560.jpg) or
or ![[image]](images/dcleq0561.jpg) ). Thus, B = 1 is not a cause of WIN = 1 in (MV, u) according to the updated HP definition.
). Thus, B = 1 is not a cause of WIN = 1 in (MV, u) according to the updated HP definition.
By way of contrast, B = 1 and C = 1 are causes of WIN = 1 in (MV, u) according to the original HP definition (as we would expect from Theorem 2.2.3). Although B = 1 and C = 1 do not satisfy AC2(bu), they do satisfy AC2(bo). To see that B = 1 satisfies AC2(bo), take ![[image]](images/dcleq0562.jpg) and consider the witness where A = 0, C = 1, and D′ = 0. Clearly we have both that (MV, u) ⊨ [B ← 0, A ← 0, C ← 1, D′←0](WIN = 0) and that (MV, u) = [B ← 1, A ← 0, C ← 1, D′ ← 0](WIN = 1), and this continues to hold if D is set to 1 (its original value). A similar argument shows that C = 1 is a cause.
and consider the witness where A = 0, C = 1, and D′ = 0. Clearly we have both that (MV, u) ⊨ [B ← 0, A ← 0, C ← 1, D′←0](WIN = 0) and that (MV, u) = [B ← 1, A ← 0, C ← 1, D′ ← 0](WIN = 1), and this continues to hold if D is set to 1 (its original value). A similar argument shows that C = 1 is a cause.
Interestingly, none of B = 1, C = 1, or B = 1 C = 1 is a cause of WIN = 1 in (MV, u) according to the modified HP definition. This follows from Theorem 2.2.3; if B = 1 were part of a cause according to the modified HP definition, then it would be a cause according to the updated HP definition, and similarly for C = 1. It can also be seen directly: setting B = C = 0 has no effect on WIN if A = 1. The only cause of WIN = 1 in (MV, u) according to the modified HP definition is A = 1 (which, of course, is also a cause according to the original and updated definitions). ■
The fact that causes may not be singletons has implications for the difficulty of determining whether A is an actual cause of B (see Section 5.3). Although this may suggest that we should then use the original HP definition, adding extra variables if needed, this conclusion is not necessarily warranted either. For one thing, it may not be obvious when modeling a problem that extra variables are needed. Moreover, the advantages of lower complexity may be lost if sufficiently many additional variables need to be added. The modified HP definition has the benefits of both typically giving the “right” answer without the need for extra variables (but see Section 4.3), while having lower complexity than either the original and modified HP definition (again, see Section 5.3).
I conclude this section with one more example that I hope clarifies some of the details of AC2(bu) (and AC2(bo)). Recall that AC2(bu) requires that φ remain true if ![[image]](images/dcleq0563.jpg) is set to
is set to ![[image]](images/dcleq0564.jpg) , even if only a subset of the variables in
, even if only a subset of the variables in ![[image]](images/dcleq0565.jpg) are set to their values in
are set to their values in ![[image]](images/dcleq0566.jpg) and all the variables in an arbitrary subset
and all the variables in an arbitrary subset ![[image]](images/dcleq0567.jpg) of
of ![[image]](images/dcleq0568.jpg) are set to their original values
are set to their original values ![[image]](images/dcleq0569.jpg) (i.e., the values they had in the original context, where
(i.e., the values they had in the original context, where ![[image]](images/dcleq0570.jpg) ). Since I have viewed the variables in
). Since I have viewed the variables in ![[image]](images/dcleq0571.jpg) as being on the causal path to φ (although that is not quite right; see Section 2.9), we might hope that not only is setting
as being on the causal path to φ (although that is not quite right; see Section 2.9), we might hope that not only is setting ![[image]](images/dcleq0572.jpg) to
to ![[image]](images/dcleq0573.jpg) sufficient to make φ true, but it is also enough to force all the variables in
sufficient to make φ true, but it is also enough to force all the variables in ![[image]](images/dcleq0574.jpg) to their original values. Indeed, there is a definition of actual causality that makes this requirement (see the bibliographic notes). Formally, we might hope that if
to their original values. Indeed, there is a definition of actual causality that makes this requirement (see the bibliographic notes). Formally, we might hope that if ![[image]](images/dcleq0575.jpg) , then the following holds:
, then the following holds:
![[image]](images/dcleq0576.jpg) (2.1)
(2.1)
It is not hard to show (see Lemma 2.10.2) that, in the presence of (2.1), AC2(bu) can be simplified to
![[image]](images/dcleq0577.jpg)
there is no need to include the subsets Z′. Although (2.1) holds in many examples, it seems unreasonable to require it in general, as the following example shows.
Example 2.8.3 Imagine that a vote takes place. For simplicity, two people vote. The measure is passed if at least one of them votes in favor. In fact, both of them vote in favor, and the measure passes. This version of the story is almost identical to the situation where either a match or a lightning strike suffices to bring about a forest fire. If we use V1 and V2 to denote how the voters vote (Vi = 0 if voter i votes against and Vi = 1 if she votes in favor) and P to denote whether the measure passes (P = 1 if it passes, P = 0 if it doesn’t), then in the context where V1 = V2 = 1, it is easy to see that each of V1 = 1 and V2 = 1 is part of a cause of P = 1 according to the original and updated HP definition. However, suppose that the story is modified slightly. Now assume that there is a voting machine that tabulates the votes. Let T represent the total number of votes recorded by the machine. Clearly, T = V1 + V2 and P = 1 iff T ≥ 1. The causal network in Figure 2.10 represents this more refined version of the story.
In this more refined scenario, V1 = 1 and V2 = 1 are still both causes of P = 1 according to the original and updated HP definition. Consider V1 = 1. Take ![[image]](images/dcleq0578.jpg) and
and ![[image]](images/dcleq0579.jpg) , and consider the contingency V2 = 0. With this witness, P is counterfactually dependent on V1, so AC2(a) holds. To check that this contingency satisfies AC2(bu) (and hence also AC2(bo)), note that setting V1 to 1 and V2 to 0 results in P = 1, even if T is set to 2 (its current value). However, (2.1) does not hold here: T does not retain its original value of 2 when V1 = 1 and V2 = 0.
, and consider the contingency V2 = 0. With this witness, P is counterfactually dependent on V1, so AC2(a) holds. To check that this contingency satisfies AC2(bu) (and hence also AC2(bo)), note that setting V1 to 1 and V2 to 0 results in P = 1, even if T is set to 2 (its current value). However, (2.1) does not hold here: T does not retain its original value of 2 when V1 = 1 and V2 = 0.
![[image]](images/fig2-10.jpg)
Figure 2.10: A more refined voting scenario.
Since, in general, one can always imagine that a change in one variable produces some feeble change in another, it seems unreasonable to insist on the variables in ![[image]](images/dcleq0580.jpg) remaining constant; AC2(bo) and AC2(bu) require merely that changes in
remaining constant; AC2(bo) and AC2(bu) require merely that changes in ![[image]](images/dcleq0581.jpg) not affect φ. ■
not affect φ. ■
There is an intuition that causality travels along a path: A causes B, which causes C, which causes D, so there is a path from A to B to C to D. And, indeed, many accounts of causality explicitly make use of causal paths. In the original and updated HP definition, AC2 involves a partition of the endogenous variables into two sets, ![[image]](images/dcleq0582.jpg) and
and ![[image]](images/dcleq0583.jpg) . In principle, there are no constraints on what partition to use, other than the requirement that
. In principle, there are no constraints on what partition to use, other than the requirement that ![[image]](images/dcleq0584.jpg) be a subset of
be a subset of ![[image]](images/dcleq0585.jpg) . However, when introducing AC2(a), I suggested that
. However, when introducing AC2(a), I suggested that ![[image]](images/dcleq0586.jpg) can be thought of as consisting of the variables on the causal path from
can be thought of as consisting of the variables on the causal path from ![[image]](images/dcleq0587.jpg) to φ. (Recall that the notion of a causal path is defined formally in Section 2.4.) As I said, this intuition is not quite true for the updated HP definition; however, it is true for the original HP definition. In this section, I examine the role of causal paths in AC2. In showing that
to φ. (Recall that the notion of a causal path is defined formally in Section 2.4.) As I said, this intuition is not quite true for the updated HP definition; however, it is true for the original HP definition. In this section, I examine the role of causal paths in AC2. In showing that ![[image]](images/dcleq0588.jpg) is a cause of φ, I would like to show that we can take
is a cause of φ, I would like to show that we can take ![[image]](images/dcleq0589.jpg) (or
(or ![[image]](images/dcleq0590.jpg) in the case of the modified HP definition) to consist only of variables that lie on a causal path from some variable in
in the case of the modified HP definition) to consist only of variables that lie on a causal path from some variable in ![[image]](images/dcleq0591.jpg) to some variable in φ. The following example shows that this is not the case in general with the updated HP definition.
to some variable in φ. The following example shows that this is not the case in general with the updated HP definition.
Example 2.9.1 Consider the following variant of the disjunctive forest-fire scenario. Now there is a second arsonist; he will drop a lit match exactly if the first one does. Thus, we add a new variable MD′ with the equation MD′ = MD. Moreover, FF is no longer a binary variable; it has three possible values: 0, 1, and 2. We have that FF = 0 if L = MD = MD′ = 0; FF = 1 if either L = 1 and MD = MD′ or MD = MD′ = 1; and FF = 2 if MD = MD′. We can suppose that the forest burns asymmetrically (FF = 2) if exactly one of the arsonists drops a lit match (which does not happen under normal circumstances); one side of the forest is more damaged than the other (even if the lightning strikes). Call the resulting causal model ![[image]](images/dcleq0592.jpg) . Figure 2.11 shows the causal network corresponding to
. Figure 2.11 shows the causal network corresponding to ![[image]](images/dcleq0593.jpg) .
.
![[image]](images/fig2-11.jpg)
Figure 2.11: The forest fire with two arsonists.
In the context u where L = MD = 1, L = 1 is a cause of FF = 1 according to the updated HP definition. Note that there is only one causal path from L to FF: the path consisting of just the variables L and FF. But to show that L = 1 is a cause of FF = 1 according to the updated HP definition, we need to take the witness to be ({MD}, 0, 0); in particular, MD′ is part of ![[image]](images/dcleq0594.jpg) , not
, not ![[image]](images/dcleq0595.jpg) .
.
To see that this witness works, note that ![[image]](images/dcleq0596.jpg) , so AC2(a) holds. Since we have both
, so AC2(a) holds. Since we have both ![[image]](images/dcleq0597.jpg) and
and ![[image]](images/dcleq0598.jpg) , AC2(bu) also holds. However, suppose that we wanted to find a witness where the set
, AC2(bu) also holds. However, suppose that we wanted to find a witness where the set ![[image]](images/dcleq0599.jpg) (so that
(so that ![[image]](images/dcleq0600.jpg) can be the unique causal path from L to FF). What do we set MD and MD′ to in the witness? At least one of them must be 0, so that when L is set to 0, FF ≠ 1. Setting MD′ = 0 does not work:
can be the unique causal path from L to FF). What do we set MD and MD′ to in the witness? At least one of them must be 0, so that when L is set to 0, FF ≠ 1. Setting MD′ = 0 does not work: ![[image]](images/dcleq0601.jpg) , so AC2(bu) does not hold. And setting MD = 0 and MD′ = 1 does not work either, for then FF = 2, independent of the value of L, so again AC2(bu) does not hold.
, so AC2(bu) does not hold. And setting MD = 0 and MD′ = 1 does not work either, for then FF = 2, independent of the value of L, so again AC2(bu) does not hold.
By way of contrast, we can take ({MD, MD′},![[image]](images/dcleq0602.jpg) , 0) to be a witness to L = 1 being a cause according to the original HP definition; AC2(bo) holds with this witness because
, 0) to be a witness to L = 1 being a cause according to the original HP definition; AC2(bo) holds with this witness because ![[image]](images/dcleq0603.jpg) .
.
Finally, perhaps disconcertingly, L = 1 is not even part of a cause of FF = 1 in (M, u) according to the modified HP definition. That is because MD = 1 is now a cause; setting MD to 0 while keeping MD′ fixed at 1 results in FF being 2. Thus, unlike the original forest-fire example, L = 1 ∧ MD = 1 is no longer a cause of FF = 1 according to the modified HP definition. This problem disappears once we take normality into 5account; see Example 3.2.5. account (see Example 3.2.5). ■
For the original HP definition, we can take the set ![[image]](images/dcleq0604.jpg) in AC2, not just in this example, but in general, to consist only of variables that lie on a causal path from a variable in
in AC2, not just in this example, but in general, to consist only of variables that lie on a causal path from a variable in ![[image]](images/dcleq0605.jpg) to a variable in φ. Interestingly, it is also true of the modified HP definition, except in that case we have to talk about
to a variable in φ. Interestingly, it is also true of the modified HP definition, except in that case we have to talk about ![[image]](images/dcleq0606.jpg) rather than
rather than ![[image]](images/dcleq0607.jpg) because
because ![[image]](images/dcleq0608.jpg) is the analogue of
is the analogue of ![[image]](images/dcleq0609.jpg) in the modified HP definition.
in the modified HP definition.
Proposition 2.9.2 If ![[image]](images/dcleq0610.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dcleq0611.jpg) according to the original or modified HP definition, then there exists a witness
according to the original or modified HP definition, then there exists a witness ![[image]](images/dcleq0612.jpg) to this such that every variable
to this such that every variable ![[image]](images/dcleq0613.jpg) lies on a causal path in
lies on a causal path in ![[image]](images/dcleq0614.jpg) from some variable in
from some variable in ![[image]](images/dcleq0615.jpg) to some variable in φ.
to some variable in φ.
For definiteness, I take X be a variable “in φ” if, syntactically, X appears in φ, even if φ is equivalent to a formula that does not involve X. For example, if Y is a binary variable, I take Y to appear in X = 1 ∧ (Y = 1 ∨ Y = 1), although this formula is equivalent to X = 1. (The proposition is actually true even if I assume that Y does not appear in X = 1 ∧ (Y = 1 ∨ Y = 1).) The proof of the proposition can be found in Section 2.10.3.
In this section, I prove some of the results stated earlier. This section can be skipped without loss of continuity.
I repeat the statements of the theorem here (and in the later sections) for the reader’s convenience.
Theorem 2.2.3:
(a)If X = x is part of a cause of φ in ![[image]](images/dcleq0616.jpg) according to the modified HP definition, then X = x is a cause of φ in
according to the modified HP definition, then X = x is a cause of φ in ![[image]](images/dcleq0617.jpg) according to the original HP definition.
according to the original HP definition.
(b)If X = x is part of a cause of φ in ![[image]](images/dcleq0618.jpg) according to the modified HP definition, then X = x is a cause of φ in
according to the modified HP definition, then X = x is a cause of φ in ![[image]](images/dcleq0619.jpg) according to the updated HP definition.
according to the updated HP definition.
(c)If X = x is part of a cause of φ in ![[image]](images/dcleq0620.jpg) according to the updated HP definition, then X = x is a cause of φ in
according to the updated HP definition, then X = x is a cause of φ in ![[image]](images/dcleq0621.jpg) according to the original HP definition.
according to the original HP definition.
(d)If ![[image]](images/dcleq0622.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dcleq0623.jpg) according to the original HP definition, then
according to the original HP definition, then ![[image]](images/dcleq0624.jpg) (i.e.,
(i.e., ![[image]](images/dcleq0625.jpg) is a singleton).
is a singleton).
Proof: For part (a), suppose that X = x is part of a cause of φ in ![[image]](images/dcleq0626.jpg) according to the modified HP definition, so that there is a cause
according to the modified HP definition, so that there is a cause ![[image]](images/dcleq0627.jpg) such that X = x is one of its conjuncts. I claim that X = x is a cause of φ according to the original HP definition. By definition, there must exist a value
such that X = x is one of its conjuncts. I claim that X = x is a cause of φ according to the original HP definition. By definition, there must exist a value ![[image]](images/dcleq0628.jpg) and a set
and a set ![[image]](images/dcleq0629.jpg) such that if
such that if ![[image]](images/dcleq0630.jpg) , then
, then ![[image]](images/dcleq0631.jpg) . Moreover,
. Moreover, ![[image]](images/dcleq0632.jpg) is minimal.
is minimal.
To show that X = x is a cause according to the original HP definition, we must find an appropriate witness. If ![[image]](images/dcleq0633.jpg) , then it is immediate that
, then it is immediate that ![[image]](images/dcleq0634.jpg) is a witness. If
is a witness. If ![[image]](images/dcleq0635.jpg) , suppose without loss of generality that
, suppose without loss of generality that ![[image]](images/dcleq0636.jpg) , and X = X1. In general, if
, and X = X1. In general, if ![[image]](images/dcleq0637.jpg) is a vector, I write
is a vector, I write ![[image]](images/dcleq0638.jpg) to denote all components of the vector except the first one, so that
to denote all components of the vector except the first one, so that ![[image]](images/dcleq0639.jpg) . I want to show that X1 = x1 is a cause of φ in
. I want to show that X1 = x1 is a cause of φ in ![[image]](images/dcleq0640.jpg) according to the original HP definition. Clearly,
according to the original HP definition. Clearly, ![[image]](images/dcleq0641.jpg) , since
, since ![[image]](images/dcleq0642.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dcleq0643.jpg) according to the modified HP definition, so AC1 holds. The obvious candidate for a witness for AC2(a) is
according to the modified HP definition, so AC1 holds. The obvious candidate for a witness for AC2(a) is ![[image]](images/dcleq0644.jpg) , where • is the operator that concatenates two vectors so that, for example, (1, 3) • (2) = (1, 3, 2); that is, roughly speaking, we move X2, …, Xn into
, where • is the operator that concatenates two vectors so that, for example, (1, 3) • (2) = (1, 3, 2); that is, roughly speaking, we move X2, …, Xn into ![[image]](images/dcleq0645.jpg) . This satisfies AC2(a), since
. This satisfies AC2(a), since ![[image]](images/dcleq0646.jpg) by assumption. AC3 trivially holds for X1 = x1, so it remains to deal with AC2(bo). Suppose, by way of contradiction, that
by assumption. AC3 trivially holds for X1 = x1, so it remains to deal with AC2(bo). Suppose, by way of contradiction, that ![[image]](images/dcleq0647.jpg) . This means that
. This means that ![[image]](images/dcleq0647a.jpg) satisfies AC2(am), showing that AC3 (more precisely, the version of AC3 appropriate for the modified HP definition) is violated (taking
satisfies AC2(am), showing that AC3 (more precisely, the version of AC3 appropriate for the modified HP definition) is violated (taking ![[image]](images/dcleq0647b.jpg) ) as the witness), and
) as the witness), and ![[image]](images/dcleq0647c.jpg) is not a cause of φ in
is not a cause of φ in ![[image]](images/dcleq0647d.jpg) according to the modified HP definition, a contradiction. Thus,
according to the modified HP definition, a contradiction. Thus, ![[image]](images/dcleq0647e.jpg) .
.
This does not yet show that AC2(bo) holds: there might be some subset ![[image]](images/dcleq0648.jpg) of variables in
of variables in ![[image]](images/dcleq0649.jpg) that change value when
that change value when ![[image]](images/dcleq0650.jpg) is set to
is set to ![[image]](images/dcleq0651.jpg) and
and ![[image]](images/dcleq0652.jpg) is set to
is set to ![[image]](images/dcleq0653.jpg) , and when these variables are set to their original values in
, and when these variables are set to their original values in ![[image]](images/dcleq0654.jpg) does not hold, thus violating AC2(bu). In more detail, suppose that there exist a set
does not hold, thus violating AC2(bu). In more detail, suppose that there exist a set ![[image]](images/dcleq0655.jpg) and values
and values ![[image]](images/dcleq0656.jpg) for each variable
for each variable ![[image]](images/dcleq0657.jpg) such that (i)
such that (i) ![[image]](images/dcleq0658.jpg) and (ii)
and (ii) ![[image]](images/dcleq0659.jpg) . But then
. But then ![[image]](images/dcleq0660.jpg) is not a cause of φ in
is not a cause of φ in ![[image]](images/dcleq0660a.jpg) according the modified HP definition. Condition (ii) shows that AC2(am) is satisfied for
according the modified HP definition. Condition (ii) shows that AC2(am) is satisfied for ![[image]](images/dcleq0661.jpg) , taking
, taking ![[image]](images/dcleq0662.jpg) as the witness, so again AC3 is violated. It follows that AC2(bu) holds, completing the proof.
as the witness, so again AC3 is violated. It follows that AC2(bu) holds, completing the proof.
The proof of part (b) is similar in spirit. Indeed, we just need to show one more thing. For AC2(bu), we must show that if ![[image]](images/dcleq0663.jpg) , and
, and ![[image]](images/dcleq0663a.jpg) , then
, then
![[image]](images/dcleq0664.jpg) (2.2)
(2.2)
(Here I am using the abuse of notation that I referred to in Section 2.2.2, where if ![[image]](images/dcleq0665.jpg) and
and ![[image]](images/dcleq0666.jpg) , I write
, I write ![[image]](images/dcleq0667.jpg) , with the intention that the components of
, with the intention that the components of ![[image]](images/dcleq0668.jpg) not included in
not included in ![[image]](images/dcleq0669.jpg) are ignored.) It follows easily from AC1 that (2.2) holds if
are ignored.) It follows easily from AC1 that (2.2) holds if ![[image]](images/dcleq0670.jpg) . And if (2.2) does not hold for some strict nonempty subset
. And if (2.2) does not hold for some strict nonempty subset ![[image]](images/dcleq0671.jpg) of
of ![[image]](images/dcleq0672.jpg) , then
, then ![[image]](images/dcleq0673.jpg) is not a cause of φ according to the modified HP definition because AC3 does not hold; AC2(am) is satisfied for
is not a cause of φ according to the modified HP definition because AC3 does not hold; AC2(am) is satisfied for ![[image]](images/dcleq0674.jpg) .
.
For part (c), the proof is again similar in spirit. Indeed, the proof is identical up to the point where we must show that AC2(bo) holds. Now if ![[image]](images/dcleq0675.jpg) and
and ![[image]](images/dcleq0676.jpg) , then
, then ![[image]](images/dcleq0677.jpg) satisfies AC2(a) (taking
satisfies AC2(a) (taking ![[image]](images/dcleq0678.jpg) as the witness). It also satisfies AC2(bu), since
as the witness). It also satisfies AC2(bu), since ![[image]](images/dcleq0679.jpg) satisfies AC2(bu), by assumption. Thus, the version of AC3 appropriate for the updated HP definition is violated.
satisfies AC2(bu), by assumption. Thus, the version of AC3 appropriate for the updated HP definition is violated.
Finally, for part (d), the proof is yet again similar in spirit. Suppose that ![[image]](images/dcleq0680.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dcleq0681.jpg) according to the original HP definition and
according to the original HP definition and ![[image]](images/dcleq0682.jpg) . Let X = x be a conjunct of
. Let X = x be a conjunct of ![[image]](images/dcleq0683.jpg) . Again, we can show that X = x is a cause of φ in
. Again, we can show that X = x is a cause of φ in ![[image]](images/dcleq0684.jpg) according to the original HP definition, which is exactly what is needed to prove part (d), using essentially the same argument as above. I leave the details to the reader. ■
according to the original HP definition, which is exactly what is needed to prove part (d), using essentially the same argument as above. I leave the details to the reader. ■
2.10.2 Proof of Proposition 2.4.6
In this section, I prove Proposition 2.4.6. I start with a simple lemma that states a key (and obvious!) property of causal paths: if there is no causal path from X to Y, then changing the value of X cannot change the value of Y. This fact is made precise in the following lemma. Although it is intuitively obvious, proving it carefully requires a little bit of work. I translate the proof into statisticians’ notation as well.
Lemma 2.10.1 If Y and all the variables in ![[image]](images/dcleq0685.jpg) are endogenous,
are endogenous, ![[image]](images/dcleq0686.jpg) , and there is no causal path in
, and there is no causal path in ![[image]](images/dcleq0687.jpg) from a variable in
from a variable in ![[image]](images/dcleq0688.jpg) to Y, then for all sets
to Y, then for all sets ![[image]](images/dcleq0689.jpg) of variables disjoint from
of variables disjoint from ![[image]](images/dcleq0690.jpg) and Y, and all settings
and Y, and all settings ![[image]](images/dcleq0691.jpg) and
and ![[image]](images/dcleq0692.jpg) for
for ![[image]](images/dcleq0693.jpg) , y for Y, and
, y for Y, and ![[image]](images/dcleq0694.jpg) for
for ![[image]](images/dcleq0695.jpg) , we have
, we have
![[image]](images/dcleq0696.jpg)
and
![[image]](images/dcleq0697.jpg)
Proof: Define the maximum distance of a variable Y in a causal setting ![[image]](images/dcleq0698.jpg) , denoted maxdist (Y), to be the length of the longest causal path in
, denoted maxdist (Y), to be the length of the longest causal path in ![[image]](images/dcleq0699.jpg) from an exogenous variable to Y. We prove both parts of the result simultaneously by induction on maxdist (Y). If maxdist (Y) = 1, then the value of Y depends only on the values of the exogenous variables, so the result trivially holds. If maxdist (Y) > 1, let Z1, …, Zk be the endogenous variables on which Y depends. These are the parents of Y in the causal network (i.e., these are exactly the endogenous variables Z such that there is an edge from Z to Y in the causal network). For each Z ∈ {Z1, …, Zk}, maxdist (Z) < maxdist (Y): for each causal path in
from an exogenous variable to Y. We prove both parts of the result simultaneously by induction on maxdist (Y). If maxdist (Y) = 1, then the value of Y depends only on the values of the exogenous variables, so the result trivially holds. If maxdist (Y) > 1, let Z1, …, Zk be the endogenous variables on which Y depends. These are the parents of Y in the causal network (i.e., these are exactly the endogenous variables Z such that there is an edge from Z to Y in the causal network). For each Z ∈ {Z1, …, Zk}, maxdist (Z) < maxdist (Y): for each causal path in ![[image]](images/dcleq0700.jpg) from an exogenous variable to Z, there is a longer path to Y, namely, the one formed by adding the edge from Z to Y. Moreover, there is no causal path in
from an exogenous variable to Z, there is a longer path to Y, namely, the one formed by adding the edge from Z to Y. Moreover, there is no causal path in ![[image]](images/dcleq0701.jpg) from a variable in
from a variable in ![[image]](images/dcleq0702.jpg) to any of Z1, …, Zk nor is any of Z1, …, Zk in
to any of Z1, …, Zk nor is any of Z1, …, Zk in ![[image]](images/dcleq0703.jpg) (for otherwise there would be a causal path in
(for otherwise there would be a causal path in ![[image]](images/dcleq0704.jpg) from a variable in
from a variable in ![[image]](images/dcleq0705.jpg) to Y, contradicting the assumption of the lemma). Thus, the inductive hypothesis holds for each of Z1, …, Zk. Since the value of each of Z1, …, Zk does not change when we change the setting of
to Y, contradicting the assumption of the lemma). Thus, the inductive hypothesis holds for each of Z1, …, Zk. Since the value of each of Z1, …, Zk does not change when we change the setting of ![[image]](images/dcleq0706.jpg) from
from ![[image]](images/dcleq0707.jpg) to
to ![[image]](images/dcleq0708.jpg) , and the value of Y depends only on the values of Z1, …, Zk and
, and the value of Y depends only on the values of Z1, …, Zk and ![[image]](images/dcleq0709.jpg) (i.e., the values of the exogenous variables), the value of Y cannot change either. ■
(i.e., the values of the exogenous variables), the value of Y cannot change either. ■
I can now prove Proposition 2.4.6. I restate it for the reader’s convenience.
Proposition 2.4.6: Suppose that X1 = x1 is a but-for cause of X2 = x2 in the causal setting ![[image]](images/dcleq0710.jpg) , X2 = x2 is a but-for cause of X3 = x3 in
, X2 = x2 is a but-for cause of X3 = x3 in ![[image]](images/dcleq0711.jpg) and the following two conditions hold:
and the following two conditions hold:
(a)for every value ![[image]](images/dcleq0712.jpg) , there exists a value
, there exists a value ![[image]](images/dcleq0713.jpg) such that
such that ![[image]](images/dcleq0714.jpg) ;
;
(b)X2 is on every causal path in ![[image]](images/dcleq0715.jpg) from X1 to X3.
from X1 to X3.
Then X1 = x1 is a but-for cause of X3 = x3.
Proof: Since X2 = x2 is a but-for cause of X3 = x3 in ![[image]](images/dcleq0716.jpg) , there exists a value
, there exists a value ![[image]](images/dcleq0717.jpg) such that
such that ![[image]](images/dcleq0718.jpg) (i.e.,
(i.e., ![[image]](images/dcleq0719.jpg) ). Choose
). Choose ![[image]](images/dcleq0720.jpg) such that
such that ![[image]](images/dcleq0721.jpg) (i.e.,
(i.e., ![[image]](images/dcleq0722.jpg) . By assumption, there exists a value
. By assumption, there exists a value ![[image]](images/dcleq0723.jpg) such that
such that ![[image]](images/dcleq0724.jpg) (i.e.,
(i.e., ![[image]](images/dcleq0725.jpg) . I claim that
. I claim that ![[image]](images/dcleq0726.jpg) (i.e.,
(i.e., ![[image]](images/dcleq0727.jpg) . This follows from a more general claim. I show that if Y is on a causal path from X2 to X3, then
. This follows from a more general claim. I show that if Y is on a causal path from X2 to X3, then
![[image]](images/dcleq0728.jpg) (2.3)
(2.3)
(i.e., ![[image]](images/dcleq0729.jpg) ).
).
Define a partial order ⪯ on endogenous variables that lie on a causal path from X2 to X3 by taking Y1 ≺ Y2 if Y1 precedes Y2 on some causal path from X2 to X3. Since M is a recursive model, if Y1 and Y2 are distinct variables and Y1 ≺ Y2, we cannot have Y2 ≺ Y1 (otherwise there would be a cycle). I prove (2.3) by induction on the ≺ ordering. The least element in this ordering is clearly X2; X2 must come before every other variable on a causal path from X2 to X3. ![[image]](images/dcleq0730.jpg) (i.e.,
(i.e., ![[image]](images/dcleq0731.jpg) ) by assumption, and clearly
) by assumption, and clearly ![[image]](images/dcleq0732.jpg) (i.e.,
(i.e., ![[image]](images/dcleq0733.jpg) . Thus, (2.3) holds for X2. Thus completes the base case of the induction.
. Thus, (2.3) holds for X2. Thus completes the base case of the induction.
For the inductive step, let Y be a variable that lies on a causal path in ![[image]](images/dcleq0734.jpg) from X2 and X3, and suppose that (2.3) holds for all variables Y′ such that Y′? Y. Let Z1, …, Zk be the endogenous variables that Y depends on in M. For each of these variables Zi, either there is a causal path in
from X2 and X3, and suppose that (2.3) holds for all variables Y′ such that Y′? Y. Let Z1, …, Zk be the endogenous variables that Y depends on in M. For each of these variables Zi, either there is a causal path in ![[image]](images/dcleq0735.jpg) from X1 to Zi or there is not. If there is, then the path from X1 to Zi can be extended to a directed path P from X1 to X3 by going from X1 to Zi, from Zi to Y, and from Y to X3 (since Y lies on a causal path in
from X1 to Zi or there is not. If there is, then the path from X1 to Zi can be extended to a directed path P from X1 to X3 by going from X1 to Zi, from Zi to Y, and from Y to X3 (since Y lies on a causal path in ![[image]](images/dcleq0736.jpg) from X2 to X3). Since, by assumption, X2 lies on every causal path in
from X2 to X3). Since, by assumption, X2 lies on every causal path in ![[image]](images/dcleq0737.jpg) from X1 to X3, X2 must lie on P. Moreover, X2 must precede Y on P. (Proof: Since Y lies on a path P′ from X2 to X3, X2 must precede Y on P′. If Y precedes X2 on P, then there is a cycle, which is a contradiction.) Since Zi precedes Y on P, it follows that Zi ≺ Y, so by the inductive hypothesis,
from X1 to X3, X2 must lie on P. Moreover, X2 must precede Y on P. (Proof: Since Y lies on a path P′ from X2 to X3, X2 must precede Y on P′. If Y precedes X2 on P, then there is a cycle, which is a contradiction.) Since Zi precedes Y on P, it follows that Zi ≺ Y, so by the inductive hypothesis, ![[image]](images/dcleq0738.jpg) iff
iff ![[image]](images/dcleq0739.jpg) (i.e.,
(i.e., ![[image]](images/dcleq0740.jpg) .
.
Now if there is no causal path in ![[image]](images/dcleq0741.jpg) from X1 to Zi, then there also cannot be a causal path P from X2 to Zi (otherwise there would be a causal path in
from X1 to Zi, then there also cannot be a causal path P from X2 to Zi (otherwise there would be a causal path in ![[image]](images/dcleq0742.jpg) from X1 to Zi formed by appending P to a causal path from X1 to X2, which must exist because, if not, it easily follows from Lemma 2.10.1 that X1 = x1 would not be a cause of X2 = x2). Since there is no causal path in
from X1 to Zi formed by appending P to a causal path from X1 to X2, which must exist because, if not, it easily follows from Lemma 2.10.1 that X1 = x1 would not be a cause of X2 = x2). Since there is no causal path in ![[image]](images/dcleq0743.jpg) from X1 to Zi, we must have that
from X1 to Zi, we must have that ![[image]](images/dcleq0744.jpg) iff
iff ![[image]](images/dcleq0745.jpg) (i.e.,
(i.e., ![[image]](images/dcleq0746.jpg) iff
iff ![[image]](images/dcleq0747.jpg) .
.
Since the value of Y depends only on the values of Z1, …, Zk and ![[image]](images/dcleq0748.jpg) , and I have just shown that
, and I have just shown that ![[image]](images/dcleq0749.jpg) iff
iff ![[image]](images/dcleq0750.jpg) (i.e.,
(i.e., ![[image]](images/dcleq0751.jpg) iff
iff ![[image]](images/dcleq0752.jpg) it follows that
it follows that ![[image]](images/dcleq0753.jpg) iff
iff ![[image]](images/dcleq0754.jpg) (i.e.,
(i.e., ![[image]](images/dcleq0755.jpg) ).
).
This completes the proof of the induction step. Since X3 is on a causal path in ![[image]](images/dcleq0756.jpg) from X2 to X3, it now follows that
from X2 to X3, it now follows that ![[image]](images/dcleq0757.jpg) iff
iff ![[image]](images/dcleq0758.jpg) (i.e.,
(i.e., ![[image]](images/dcleq0759.jpg) iff
iff ![[image]](images/dcleq0760.jpg) ). Since
). Since ![[image]](images/dcleq0761.jpg) (i.e.,
(i.e., ![[image]](images/dcleq0762.jpg) ) by construction, we have that
) by construction, we have that ![[image]](images/dcleq0763.jpg) (i.e.,
(i.e., ![[image]](images/dcleq0764.jpg) ), as desired. Thus, X1 = x1 is a but-for cause for X3 = x3. ■
), as desired. Thus, X1 = x1 is a but-for cause for X3 = x3. ■
2.10.3 Proof of Proposition 2.9.2
In this section, I prove Proposition 2.9.2.
Proposition 2.9.2: If ![[image]](images/dcleq0765.jpg) is cause of φ in
is cause of φ in ![[image]](images/dcleq0766.jpg) according to the original or modified HP definition, then there exists a witness
according to the original or modified HP definition, then there exists a witness ![[image]](images/dcleq0767.jpg) to this such that every variable
to this such that every variable ![[image]](images/dcleq0768.jpg) lies on a causal path in
lies on a causal path in ![[image]](images/dcleq0769.jpg) from some variable in
from some variable in ![[image]](images/dcleq0770.jpg) to some variable in φ.
to some variable in φ.
To prove the result, I need to prove a general property of causal models, one sufficiently important to be an axiom in the axiomatization of causal reasoning given in Section 5.4.
Lemma 2.10.2 If ![[image]](images/dcleq0771.jpg) , then
, then ![[image]](images/dcleq0772.jpg) if and only if
if and only if ![[image]](images/dcleq0773.jpg) .
.
Proof: In the unique solution to the equations when ![[image]](images/dcleq0774.jpg) is set to
is set to ![[image]](images/dcleq0775.jpg) ,
, ![[image]](images/dcleq0776.jpg) . So the unique solution to the equations when
. So the unique solution to the equations when ![[image]](images/dcleq0777.jpg) is set to
is set to ![[image]](images/dcleq0778.jpg) is the same as the unique solution to the equations when
is the same as the unique solution to the equations when ![[image]](images/dcleq0779.jpg) is set to
is set to ![[image]](images/dcleq0780.jpg) and
and ![[image]](images/dcleq0781.jpg) is set to
is set to ![[image]](images/dcleq0782.jpg) . The result now follows immediately. ■
. The result now follows immediately. ■
With this background, I can prove Proposition 2.9.2.
Proof of Proposition 2.9.2: Suppose that ![[image]](images/dcleq0783.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dcleq0784.jpg) with witness
with witness ![[image]](images/dcleq0785.jpg) according to the original (resp., modified) HP definition. Let
according to the original (resp., modified) HP definition. Let ![[image]](images/dcleq0786.jpg) , let
, let ![[image]](images/dcleq0787.jpg) consist of the variables in
consist of the variables in ![[image]](images/dcleq0788.jpg) that lie on a causal path in
that lie on a causal path in ![[image]](images/dcleq0789.jpg) from some variable in
from some variable in ![[image]](images/dcleq0790.jpg) to some variable in φ, and let
to some variable in φ, and let ![[image]](images/dcleq0791.jpg) . Notice that
. Notice that ![[image]](images/dcleq0792.jpg) is a superset of
is a superset of ![[image]](images/dcleq0793.jpg) . Let
. Let ![[image]](images/dcleq0794.jpg) . The proof diverges slightly now depending on whether we consider the original or modified HP definition. In the case of the original HP definition, let yj be the value of Yj such that
. The proof diverges slightly now depending on whether we consider the original or modified HP definition. In the case of the original HP definition, let yj be the value of Yj such that ![[image]](images/dcleq0795.jpg) ; in the case of the modified HP definition, let yj be the value of Yj such that
; in the case of the modified HP definition, let yj be the value of Yj such that ![[image]](images/dcleq0796.jpg) . I claim that
. I claim that ![[image]](images/dcleq0797.jpg) is a witness to
is a witness to ![[image]](images/dcleq0798.jpg) being a cause of φ in
being a cause of φ in ![[image]](images/dcleq0799.jpg) according to the original (resp., modified) HP definition. (Recall from the proof of Theorem 2.2.3 that
according to the original (resp., modified) HP definition. (Recall from the proof of Theorem 2.2.3 that ![[image]](images/dcleq0800.jpg) denotes the result of concatenating the vectors
denotes the result of concatenating the vectors ![[image]](images/dcleq0801.jpg) and
and ![[image]](images/dcleq0802.jpg) .) Once I prove this, I will have proved the proposition.
.) Once I prove this, I will have proved the proposition.
Since ![[image]](images/dcleq0803.jpg) is a cause of φ by assumption, AC1 and AC3 hold; they are independent of the witness. This suffices to prove that AC2(a) and AC2(bo) (resp., AC2(am)) hold for this witness.
is a cause of φ by assumption, AC1 and AC3 hold; they are independent of the witness. This suffices to prove that AC2(a) and AC2(bo) (resp., AC2(am)) hold for this witness.
Since ![[image]](images/dcleq0804.jpg) is a witness to
is a witness to ![[image]](images/dcleq0805.jpg) being a cause of φ in
being a cause of φ in ![[image]](images/dcleq0806.jpg) according to the original (resp., modified) HP definition, by AC2(a) (resp., AC2(am)), it follows that
according to the original (resp., modified) HP definition, by AC2(a) (resp., AC2(am)), it follows that
![[image]](images/dcleq0807.jpg) (2.4)
(2.4)
Since no variable in ![[image]](images/dcleq0808.jpg) is on a causal path in
is on a causal path in ![[image]](images/dcleq0809.jpg) from a variable in
from a variable in ![[image]](images/dcleq0810.jpg) to a variable in φ, for each
to a variable in φ, for each ![[image]](images/dcleq0811.jpg) , either there is no causal path in
, either there is no causal path in ![[image]](images/dcleq0812.jpg) from a variable in
from a variable in ![[image]](images/dcleq0813.jpg) to Y or there is no causal path in
to Y or there is no causal path in ![[image]](images/dcleq0814.jpg) from Y to a variable in φ (or both). Without loss of generality, we can assume that the variables in
from Y to a variable in φ (or both). Without loss of generality, we can assume that the variables in ![[image]](images/dcleq0815.jpg) are ordered so that there is no causal path in
are ordered so that there is no causal path in ![[image]](images/dcleq0816.jpg) from a variable in
from a variable in ![[image]](images/dcleq0817.jpg) to any of the first j variables, Y1, …, Yj, and there is no causal path in
to any of the first j variables, Y1, …, Yj, and there is no causal path in ![[image]](images/dcleq0818.jpg) from any of the last k − j variables, Yj+1, …, Yk, to a variable in φ.
from any of the last k − j variables, Yj+1, …, Yk, to a variable in φ.
I first do the argument in the case of the modified HP definition. In this case, ![[image]](images/dcleq0819.jpg) must be the value of the variables in
must be the value of the variables in ![[image]](images/dcleq0820.jpg) in context
in context ![[image]](images/dcleq0821.jpg) ; by definition,
; by definition, ![[image]](images/dcleq0822.jpg) is the value of the variables in
is the value of the variables in ![[image]](images/dcleq0823.jpg) . Thus,
. Thus, ![[image]](images/dcleq0824.jpg) is a legitimate witness for AC2(am). Moreover, since
is a legitimate witness for AC2(am). Moreover, since ![[image]](images/dcleq0825.jpg) , by Lemma 2.10.2, we have
, by Lemma 2.10.2, we have
![[image]](images/dcleq0826.jpg)
Since there is no causal path in ![[image]](images/dcleq0827.jpg) from
from ![[image]](images/dcleq0828.jpg) to any of Y1, …, Yj, by Lemma 2.10.1, it follows that
to any of Y1, …, Yj, by Lemma 2.10.1, it follows that
![[image]](images/dcleq0829.jpg) (2.5)
(2.5)
Thus, by (2.4), (2.5), and Lemma 2.10.2, it follows that
![[image]](images/dcleq0830.jpg) (2.6)
(2.6)
Finally, since there is no causal path in ![[image]](images/dcleq0831.jpg) from any of Yj+1, …, Yk to any variable in φ, it follows from (2.6) and Lemma 2.10.1 that
from any of Yj+1, …, Yk to any variable in φ, it follows from (2.6) and Lemma 2.10.1 that
![[image]](images/dcleq0832.jpg)
so AC2(am) holds, and ![[image]](images/dcleq0833.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dcleq0834.jpg) according to the modified HP definition with witness
according to the modified HP definition with witness ![[image]](images/dcleq0835.jpg) .
.
We have to work a little harder in the case of the original HP definition (although the basic ideas are similar) because we can no longer assume that ![[image]](images/dcleq0836.jpg) . By the definition of
. By the definition of ![[image]](images/dcleq0837.jpg) in this case, we have
in this case, we have ![[image]](images/dcleq0838.jpg) . Thus, by Lemma 2.10.2,
. Thus, by Lemma 2.10.2,
![[image]](images/dcleq0839.jpg)
This shows that AC2(a) holds for the witness ![[image]](images/dcleq0840.jpg) .
.
For AC2(bo), we must show that ![[image]](images/dcleq0841.jpg) . By assumption,
. By assumption,
![[image]](images/dcleq0842.jpg) (2.7)
(2.7)
If Y ∈ {Y1, …, Yj}, then by choice of y, ![[image]](images/dcleq0843.jpg) . Thus, by Lemma 2.10.1,
. Thus, by Lemma 2.10.1,
![[image]](images/dcleq0844.jpg) (2.8)
(2.8)
By (2.7), (2.8), and Lemma 2.10.2,
![[image]](images/dcleq0845.jpg) (2.9)
(2.9)
Finally, since there is no causal path in ![[image]](images/dcleq0846.jpg) from any of Yj+1, …, Yk to a variable in φ, it follows from (2.9) and Lemma 2.10.1 that
from any of Yj+1, …, Yk to a variable in φ, it follows from (2.9) and Lemma 2.10.1 that
![[image]](images/dcleq0847.jpg)
Thus, ![[image]](images/dcleq0848.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dcleq0849.jpg) according to the original HP definition with witness
according to the original HP definition with witness ![[image]](images/dcleq0850.jpg) . ■
. ■
The use of structural equations in models for causality goes back to the geneticist Sewall Wright [1921] (see [Goldberger 1972] for a discussion). Herb Simon [1953], who won a Nobel Prize in Economics (and, in addition, made fundamental contributions to Computer Science), and the econometrician Trygve Haavelmo [1943] also made use of structural equations. The formalization used here is due to Judea Pearl, who has been instrumental in pushing for this approach to causality. Pearl [2000] provides a detailed discussion of structural equations, their history, and their use.
The assumption that the model is recursive is standard in the literature. The usual definition says that if the model is recursive, then there is a total order ⪯ of the variables such that X affects Y only if X ⪯ Y. I have made two changes to the usual definition here. The first is to allow the order to be partial; the second is to allow it to depend on the context. As the discussion of the rock-throwing example (Example 2.3.3) shows, the second assumption is useful and makes the definition more general; a good model of the rock-throwing example might well include contexts where Billy hits before Suzy if they both throw. Although it seems more natural to me to assume a partial order as I have done here, since the partial order can be read off the causal network, assuming that the order is partial is actually equivalent to assuming that it is total. Every total order is a partial order, and it is well known that every partial order can be extended (typically, in many ways) to a total order. If ⪯′ is a total order that extends ⪯ and X affects Y only if X ⪯ Y, then certainly X affects Y only if X ⪯′ Y. Allowing the partial order to depend on the context ![[image]](images/dcleq0851.jpg) is also nonstandard, but a rather minimal change.
is also nonstandard, but a rather minimal change.
As I said in the notes to Chapter 1, the original HP definition was introduced by Halpern and Pearl in [Halpern and Pearl 2001]; it was updated in [Halpern and Pearl 2005a]; the modified definition was introduced in [Halpern 2015a]. These definitions were inspired by Pearl’s original notion of a causal beam [Pearl 1998]. (The definition of causal beam in [Pearl 2000, Chapter 10] is a modification of the original definition that takes into account concerns raised in an early version of [Halpern and Pearl 2001].) Interestingly, according to the causal beam definition, A qualifies as an actual cause of B only if something like AC2(am) rather than AC2(a) holds; otherwise it is called a contributory cause. The distinction between actual cause and contributory cause is lost in the original and updated HP definition. To some extent, it resurfaces in the modified HP definition; in some cases, what the causal beam definition would classify as a contributory cause but not an actual cause would be classified as part of a cause but not a cause according to the modified HP definition.
Although I focus on (variants of) the HP definition of causality in this book, it is not the only definition of causality that is given in terms of structural equations. Besides Pearl’s causal beam notion, other definitions were given by (among others) Glymour and Wimberly [2007], Hall [2007], Hitchcock [2001, 2007], and Woodward [2003]. Problems have been pointed out with all these definitions; see [Halpern 2015a] for a discussion of some of them. As I mentioned in Chapter 1, there are also definitions of causality that use counterfactuals without using structural equations. The best known is due to Lewis [1973a, 2000]. Paul and Hall [2013] cover a number of approaches that attempt to reduce causality to counterfactuals.
Proposition 2.2.2 and parts (a) and (b) of Theorem 2.2.3 are taken from [Halpern 2015a]. Part (d) of Theorem 2.2.3, the fact that with the original HP definition causes are always single conjuncts, was proved (independently) by Hopkins [2001] and Eiter and Lukasiewicz [2002].
Much of the material in Sections 2.1–2.3 is taken from [Halpern and Pearl 2005a]. The formal definition of causal model is taken from [Halpern 2000]. Note that in the literature (especially the statistics literature), what I call here “variables” are called random variables.
In the philosophy community, counterfactuals are typically defined in terms of “closest worlds” [Lewis 1973b; Stalnaker 1968]; a statement of the form “if A were the case then B would be true” is taken to be true if in the “closest world(s)” to the actual world where A is true, B is also true. The modification of equations may be given a simple “closest world” interpretation: the solution of the equations obtained by replacing the equation for Y with the equation Y = y, while leaving all other equations unaltered, can be viewed as the closest world to the actual world where Y = y.
The asymmetry embodied in the structural equations (i.e., the fact that variables on the left- and right-hand sides of the equality sign are treated differently) can be understood in terms of closest worlds. Suppose that in the actual world, the arsonist does not drop a match, there is no lightning, and the forest does not burn down. If either the match or lightning suffices to start the fire, then in the closest world to the actual world where the arsonist drops a lit match, the forest burns down. However, it is not necessarily the case that the arsonist drops a match in the world closest to the actual world where the forest burns down. The formal connection between causal models and closest-world semantics for counterfactuals is somewhat subtle; see [Briggs 2012; Galles and Pearl 1998; Halpern 2013; Zhang 2013] for further discussion.
The question of whether there is some circularity in using causal models, where the structural equations can arguably be viewed as encoding causal relationships, to provide a model of actual causality was discussed by Woodward [2003]. As he observed, if we intervene to set X to x, the intervention can be viewed as causing X to have value x. But we are not interested in defining a causal relationship between interventions and the values of variables intervened on. Rather, we are interested in defining a causal relation between the values of some variables and the values of otherwise; for example, we want to say that the fact that X = x in the actual world is a cause of Y = y in the actual world. As Woodward points out (and I agree), the definition of actual causality depends (in part) on the fact that intervening on X by setting it to x causes X = x, but there is no circularity in this dependence.
The causal networks that are used to describe the equations are similar in spirit to Bayesian networks, which have been widely used to represent and reason about (conditional) dependencies in probability distributions. Indeed, once we add probability to the picture as in Section 2.5, the connection is even closer. Historically, Judea Pearl [1988, 2000] introduced Bayesian networks for probabilistic reasoning and then applied them to causal reasoning. This similarity to Bayesian networks will be exploited in Chapter 5 to provide insight into when we can obtain compact representations of causal models.
Spirtes, Glymour, and Scheines [1993] study causality by working directly with graphs, not structural equations. They consider type causality rather than actual causality; their focus is on (algorithms for) discovering causal structure and causal influence. This can be viewed as work that will need to be done to construct the structural equations that I am taking as given here. The importance of choosing the “right” set of variables comes out clearly in the Spirtes et al. framework as well.
The difference between conditions and causes in the law is discussed by Katz [1987] and Mackie [1965], among others.
In the standard philosophical account, causality relates events, that is, for A to be a cause of B, A and B have to be events. But what counts as an event is open to dispute. There are different theories of events. (Casati and Varzi [2014] provide a recent overview of this work; Paul and Hall [2013, pp. 58–60] discuss its relevance to theories of causality.) A major issue is whether something not happening counts as an event [Paul and Hall 2013, pp. 178–182]. (This issue is also related to that of whether omissions count as causes, discussed earlier.) The As and Bs that are the relata of causality in the HP definition are arguably closer to what philosophers have called true propositions (or facts) [Mellor 2004]. Elucidating the relationship between all these notions is well beyond the scope of this book.
Although I have handled the rock-throwing example here by just adding two additional variables (BH and SH), as I said, this is only one of many ways to capture the fact that Suzy’s rock hit the bottle and Billy’s did not. The alternative of using variables indexed by time was considered in [Halpern and Pearl 2005a].
Examples 2.3.4 (double prevention), 2.3.5 (omissions as causes), and 2.4.1 (lack of transitivity) are due to Hall; their descriptions are taken from (an early version of) [Hall 2004]. Again, these problems are well known and were mentioned in the literature much earlier. See Chapter 3 for more discussion of causation by omission and the notes to that chapter for references.
Example 2.3.6 is due to Paul [2000]. In [Halpern and Pearl 2005a], it was modeled a little differently, using variables LT (for train is on the left track) and RT (for train is on the right track). Thus, in the actual context, where the engineer flips the switch and the train goes down the right track, we have F = 1, LT = 0, and RT = 0. With this choice of variables, all three variants of the HP definition declare F = 1 a cause of A = 1 (we can fix RT at its actual value of 0 to get the counterfactual dependence of A on F). This problem can be dealt with using normality considerations (see the last paragraph of Example 3.4.3). In any case, as Hitchock and I pointed out [Halpern and Hitchcock 2010], this choice of variables is somewhat problematic because LT and RT are not independent. What would it mean to set both LT and RT to 1, for example? That the train is simultaneously going down both tracks? Using LB and FB, as done in [Halpern and Hitchcock 2010], captures the essence of Hall’s story while avoiding this problem. The issue of being able to set variables independently is discussed in more detail in Section 4.6.
Example 2.3.8 is taken from [Halpern 2015a].
O’Connor [2012] says that, each year, an estimated 4,000 cases of “retained surgical items” are reported in the United States and discusses a lawsuit resulting from one such case.
Example 2.3.7 is due to Bas van Fraassen and was introduced by Schaffer [2000b] under the name trumping preemption. Schaffer (and Lewis [2000]) claimed that, because orders from higher-ranking officers trump those of lower-ranking officers, the captain is a cause of the charge and the sergeant is not. The case is not so clearcut to me; the analysis in the main text shows just how sensitive the determination of causality is to details of the model. Halpern and Hitchcock [2010] make the point that if C and S have range {0, 1} (and the only variables in the causal model are C, S, and P), then there is no way to capture the fact that in the case of conflicting orders, the private obeys the captain. The model of the problem that captures trumping with the extra variable SE, described in Figure 2.7, was introduced in [Halpern and Pearl 2005a].
Example 2.4.2 is due to McDermott [1995], who also gives other examples of lack of transitivity, including Example 3.5.2, discussed in Chapter 3.
The question of the transitivity of causality has been the subject of much debate. As Paul and Hall [2013] say, “Causality seems to be transitive. If C causes D and D causes E, then C thereby causes E.” Indeed, Paul and Hall [2013, p. 215] suggest that “preserving transitivity is a basic desideratum for an adequate analysis of causation”. Lewis [1973a, 2000] imposes transitivity in his definition of causality by taking causality to be the transitive closure (“ancestral”, in his terminology) of a one-step causal dependence relation. But numerous examples have been presented that cast doubt on transitivity; Richard Scheines [personal communication, 2013] suggested the homeostasis example. Paul and Hall [2013] give a sequence of such counterexamples, concluding that “What’s needed is a more developed story, according to which the inference from ‘C causes D’ and ‘D causes E’ to ‘C causes E’ is safe provided such-and-such conditions obtain—where these conditions can typically be assumed to obtain, except perhaps in odd cases … ”. Hitchcock [2001] argues that the cases that create problems for transitivity fail to involve appropriate “causal routes” between the relevant events. Propositions 2.4.3, 2.4.4, and 2.4.6 can be viewed as providing other sets of conditions for when we can safely assume transitivity. These results are proved in [Halpern 2015b], from where much of the discussion in Section 2.4 is taken. Since these definitions apply only to but-for causes, which all counterfactual-based accounts (not just the HP accounts) agree should be causes, the results should hold for almost all definitions that are based on counterfactual dependence and structural equations.
As I said, there are a number of probabilistic theories of causation that identify causality with raising probability. For example, Eells and Sober [1983] take C to be a cause of E if Pr(E| Ki ∧ C) > Pr(E|Ki ∧ ¬C) for all appropriate maximal specifications Ki of causally relevant background factors, provided that these conditionals are defined (where they independently define what it means for a background factor to be causally relevant); see also [Eells 1991]. Interestingly, Eells and Sober [1983] also give sufficient conditions for causality to be transitive according to their definition. This definition does not involve counterfactuals (so the results of Section 2.4 do not apply).
There are also definitions of probabilistic causality in this spirit that do involve counterfactuals. For example, Lewis [1973a] defines a probabilistic version of his notion of dependency, by taking A to causally depend on B if and only if, had B not occurred, the chance of A’s occurring would be much less than its actual chance; he then takes causality to be the transitive closure of this causal dependence relation. There are several other ways to define causality in this spirit; see Fitelson and Hitchcock [2011] for an overview. In any case, as Example 2.5.2 shows, no matter how this is made precise, defining causality this way is problematic. Perhaps the best-known example of the problem is due to Rosen and is presented by Suppes [1970]: A golfer lines up to driver her ball, but her swing is off and she slices it badly. The slice clearly decreases the probability of a hole-in-one. But, as it happens, the ball bounces off a tree trunk at just the right angle that, in fact, the golfer gets a hole-in-one. We want to say that the slice caused the hole-in-one (and the definition given here would say that), although slicing the ball lowers the probability of a hole-in-one.
The difference between the probability of rain conditional on a low barometer reading and the probability that it rains as a result of intervening to set the barometer reading to low has been called by Pearl [2000] the difference between seeing and doing.
Examples 2.5.1, 2.5.2, and 2.5.3 are modifications of examples in [Paul and Hall 2013], with slight modifications; the original version of Example 2.5.3 is due to Frick [2009]. As I said, the idea of “pulling out the probability” is standard in computer science; see [Halpern and Tuttle 1993] for further discussion and references. Northcott [2010] defends the view that using deterministic models may capture important features of the psychology of causal judgment; he also provides a definition of probabilistic causality. Fenton-Glynn [2016] provides a definition of probabilistic causality in the spirit of the HP definitions; unfortunately, he does not consider how his approach fares on the examples in the spirit of those discussed here. Much of the material in Section 2.5 is taken from [Halpern 2014b].
Example 2.5.4 is in the spirit of an example considered by Hitchcock [2004]. In his example, both Juan and Jennifer push a source of polarized photons, which greatly increases the probability that a photon emitted by the source will be transmitted by a polarizer. In fact, the polarizer does transmit a photon. Hitchcock says, “It seems clearly wrongheaded to ask whether the transmission was really due to Juan’s push rather than Jennifer’s push. Rather … each push increased the probability of the effect (the transmission of the photon), and then it was simply a matter of chance. There are no causal facts of the matter extending beyond the probabilistic contribution made by each. This is a very simple case in which our intuitions are not clouded by tacit deterministic assumptions.”
Hitchcock’s example involves events at the microscopic level, where arguably we cannot pull out the probability. But for macroscopic events, where we can pull out the probability, as is done in Section 2.5, I believe that we can make sense out of the analogous questions, and deterministic assumptions are not at all unreasonable.
Balke and Pearl [1994] give a general discussion of how to evaluate probabilistic queries in a causal model where there is a probability on contexts.
Representation of uncertainty other than probability, including the use of sets of probability measures, are discussed in [Halpern 2003].
Lewis [1986b, Postscript C] discussed sensitive causation and emphasized that in long causal chains, causality was quite sensitive. Woodward [2006] goes into these issues in much more detail and makes the point that people’s causality judgments are clearly influenced by how sensitive the causality ascription is to changes in various other factors. He points out that one reason some people tend to view double prevention and absence of causes as not quite “first-class” causes might be that these are typically quite sensitive causes; in the language of Section 2.6, they are sufficient causes with only low probability.
Pearl and I [2005a] considered what we called strong causality, which is intended to capture some of the same intuitions behind sufficient causality. Specifically, we extended the updated definition by adding the following clause:
AC2(c). ![[image]](images/dcleq0852.jpg) for all settings
for all settings ![[image]](images/dcleq0853.jpg) .
.
Thus, instead of requiring ![[image]](images/dcleq0854.jpg) to hold in all contexts, some of the same effect is achieved by requiring that φ holds no matter what values of
to hold in all contexts, some of the same effect is achieved by requiring that φ holds no matter what values of ![[image]](images/dcleq0855.jpg) are considered. The definition given here seems somewhat closer to the intuitions and allows the consideration of probabilistic sufficient causality by putting a probability on contexts. This, in turn, makes it possible to bring out the connections between sufficient causality, normality, and blame.
are considered. The definition given here seems somewhat closer to the intuitions and allows the consideration of probabilistic sufficient causality by putting a probability on contexts. This, in turn, makes it possible to bring out the connections between sufficient causality, normality, and blame.
Although Pearl [1999, 2000] does not define the notion of sufficient causality, he does talk about the probability of sufficiency, that is, the probability that X = x is a sufficient cause of Y = y. Roughly speaking, this is the probability that setting X to x results in Y = y, conditional on X ≠ x and Y ≠ y. Ignoring the conditioning, this is very close in spirit to the definition given here. Datta et al. [2015] considered a notion close to the notion of sufficient causality defined here and pointed out that it could be used to distinguish joint and independent causality. Honoré [2010] discusses the distinction between joint and independent causation in the context of the law. Gerstenberg et al. [2015] discuss the impact of sufficient causality on people’s causality judgments.
The definition of causality in nonrecursive causal models is taken from the appendix of [Halpern and Pearl 2005a]. Strotz and Wold [1960] discuss recursive and nonrecursive models as used in econometrics. They argue that our intuitive view of causality really makes sense only in recursive models, and that once time is taken into account, a nonrecursive model can typically be viewed as recursive.
Example 2.8.1, which motivated AC2(bu), is due to Hopkins and Pearl [2003]. Example 2.8.2 is taken from [Halpern 2008]. Hall [2007] gives a definition of causality that he calls the H-account that requires (2.1) to hold (but only for ![[image]](images/dcleq0856.jpg) , not for all subsets
, not for all subsets ![[image]](images/dcleq0857.jpg) ). Example 2.8.3, which is taken from [Halpern and Pearl 2005a], shows that the H-account would not declare V1 = 1 a cause of P = 1, which seems problematic. This example also causes related problems for Pearl’s [1998, 2000] causal beam definition of causality.
). Example 2.8.3, which is taken from [Halpern and Pearl 2005a], shows that the H-account would not declare V1 = 1 a cause of P = 1, which seems problematic. This example also causes related problems for Pearl’s [1998, 2000] causal beam definition of causality.
Hall [2007], Hitchcock [2001], and Woodward [2003] are examples of accounts of causality that explicitly appeal to causal paths. In [Halpern and Pearl 2005a, Proposition A.2], it is claimed that all the variables in ![[image]](images/dcleq0858.jpg) can be taken to lie on a causal path from a variable in
can be taken to lie on a causal path from a variable in ![[image]](images/dcleq0859.jpg) to φ. As Example 2.9.1 shows, this is not true in general. In fact, the argument used in the proof of [Halpern and Pearl 2005a, Proposition A.2] does show that with AC2(bo), all the variables in
to φ. As Example 2.9.1 shows, this is not true in general. In fact, the argument used in the proof of [Halpern and Pearl 2005a, Proposition A.2] does show that with AC2(bo), all the variables in ![[image]](images/dcleq0860.jpg) can be taken to lie on a causal path from a variable in
can be taken to lie on a causal path from a variable in ![[image]](images/dcleq0861.jpg) to φ (and is essentially the argument used in the proof of Proposition 2.9.2). The definition of causality was changed from using AC2(bo) to AC2(bu) in the course of writing [Halpern and Pearl 2005a]; Proposition A.2 was not updated accordingly.
to φ (and is essentially the argument used in the proof of Proposition 2.9.2). The definition of causality was changed from using AC2(bo) to AC2(bu) in the course of writing [Halpern and Pearl 2005a]; Proposition A.2 was not updated accordingly.
Graded Causation and Normality
Perhaps the feelings that we experience when we are in love represent a normal state.
Anton Chekhov
In a number of the examples presented in Chapter 2, the HP definition gave counterintuitive ascriptions of causality. I suggested then that taking normality into account would solve these problems. In this chapter, I fill in the details of this suggestion and show that taking normality into account solves these and many other problems, in what seems to me a natural way. Although I apply ideas of normality to the HP definition, these ideas should apply equally well to a number of other approaches to defining causality.
This approach is based on the observation that norms can affect counterfactual reasoning. To repeat the Kahneman and Miller quote given in Chapter 1, “[in determining causality], an event is more likely to be undone by altering exceptional than routine aspects of the causal chain that led to it”. In the next section, I give a short discussion of issues of defaults, typicality, and normality. I then show how the HP definition can be extended to take normality into account. The chapter concludes by showing how doing this deals with the problematic examples from Chapter 2 as well as other concerns.
3.1 Defaults, Typicality, and Normality
The extended account of actual causation incorporates the concepts of defaults, typicality, and normality. These are related, although somewhat different notions:
Although this might seem like a heterogeneous mix of concepts, they are intertwined in a number of ways. For example, default inferences are successful to the extent that the default is normal in the statistical sense. Adopting the default assumption that a bird can fly facilitates successful inferences in part because most birds are able to fly. Similarly, we classify objects into types in part to group objects into classes, most of whose members share certain features. Thus, the type “bird” is useful partly because there is a suite of characteristics shared by most birds, including the ability to fly. The relationship between the statistical and prescriptive senses of “normal” is more subtle. It is, of course, quite possible for a majority of individuals to act in violation of a given moral or legal norm. Nonetheless, it seems that the different kinds of norms often serve as heuristic substitutes for one another. For example, there are well-known experiments showing that we are often poor at explicit statistical reasoning, employing instead a variety of heuristics. Rather than tracking statistics about how many individuals behave in a certain way, we might well reason about how people should behave in certain situations. The idea is that we use a script or a template for reasoning about certain situations, rather than actual statistics. Prescriptive norms of various sorts can play a role in the construction of such scripts. It is true, of course, that conflation of the different sorts of norm can sometimes have harmful consequences. Less than a hundred years ago, for example, left-handed students were often forced to learn to write with their right hands. In retrospect, this looks like an obviously fallacious inference from the premise that the majority of people write with their right hand to the conclusion that it is somehow wrong to write with the left hand. But the ease with which such an inference was made illustrates the extent to which we find it natural to glide between the different senses of “norm”.
When Kahneman and Miller say that “an event is more likely to be undone by altering exceptional than route aspects of the causal chain that led to it”, they are really talking about how we construct counterfactual situations. They are also assuming a close connection between counterfactuals and causality, since they are effectively claiming that the counterfactual situation we consider affects our causality judgment. The fact that norms influence causal judgment has been confirmed experimentally (although the experiments do not show that the influence goes via counterfactual judgments). To take just one example (see the notes at the end of the chapter for others), consider the following story from an experiment by Knobe and Fraser:
The receptionist in the philosophy department keeps her desk stocked with pens. The administrative assistants are allowed to take the pens, but faculty members are supposed to buy their own. The administrative assistants typically do take the pens. Unfortunately, so do the faculty members. The receptionist has repeatedly emailed them reminders that only administrative assistants are allowed to take the pens. On Monday morning, one of the administrative assistants encounters Professor Smith walking past the receptionist’s desk. Both take pens. Later that day, the receptionist needs to take an important message … but she has a problem. There are no pens left on her desk.
People are much more likely to view Prof. Smith as the cause of there not being pens than the administrative assistant. The HP definition does not distinguish them, calling them both causes. The extended HP definition given in the next section does allow us to distinguish them. Since the HP definition is based on counterfactuals, the key step will be to have the choice of witness be affected by normality considerations. Although the assumption that normality considerations affect counterfactual judgments does not follow immediately from the experimental evidence, it seems like a reasonable inference, given the tight connection between causality and counterfactuals.
I add normality to causal models by assuming that an agent has, in addition to a theory of causal structure (as modeled by the structural equations), a theory of “normality” or “typicality”. This theory includes statements of the form “typically, people do not put poison in coffee”. There are many ways of giving semantics to such typicality statements (see the notes at the end of the chapter). All of them give ways to compare the relative “normality” of some objects. For now, I take those objects to be the worlds in a causal model M, where a world is an assignment of values to the endogenous variables; that is, a complete description of the values of the endogenous variables in M. I discuss after Example 3.2.6 why a world here is taken to be an assignment only to the endogenous variables and not an assignment to both exogenous and endogenous variables, as in the complete assignments considered in Section 2.7. A complete assignment is essentially equivalent to the standard philosophers’ notion of a world as a maximal state of affairs, so my usage of “world” here is not quite the same as the standard philosophers’ usage. In Section 3.5, I discuss an alternative approach, which puts the normality ordering on contexts, much in the spirit of putting a probability on contexts as was done in Section 2.5. Since (in a recursive model) a context determines the values of all endogenous variables, a context can be identified with a complete assignment, and thus with the philosophers’ notion of world. But for now I stick with putting a normality ordering on worlds as I have defined them.
Most approaches to normality/typicality implicitly assume a total normality ordering on worlds: given a pair of worlds w and w′, either w is more normal than w′, w is less normal than w′, or the two worlds are equally normal. The approach used here has the advantage of allowing an extra possibility: w and w′ are incomparable as far as normality goes. (Technically, this means that the normality ordering is partial, rather than total.)
We can think of a world as a complete description of a situation given the language determined by the set of endogenous variables. Thus, a world in the forest-fire example might be one where U = (0, 1), L = 0, MD = 1, and FF = 0; the match is dropped, there is no lightning, and no forest fire. As this example shows, a “world” does not have to satisfy the equations of the causal model.
For ease of exposition, I make a somewhat arbitrary stipulation regarding terminology. In what follows, I use “default” and “typical” when talking about individual variables or equations. For example, I might say that the default value of a variable is zero or that one variable typically depends on another in a certain way. I use “normal” when talking about worlds. Thus, I say that one world is more normal than another. I assume that it is typical for endogenous variables to be related to one another in the way described by the structural equations of a model, unless there is some specific reason to think otherwise. This ensures that the downstream consequences of what is typical are themselves typical (again, in the absence of any specific reason to think otherwise).
Other than this mild restriction, I make no assumptions on what gets counted as typical. This introduces a subjective element into a causal model. Different people might well use different normality orderings, perhaps in part due to focusing on different aspects of normality (descriptive normality, typicality, prescriptive normality, etc.). This might bother those who think of causality as an objective feature of the world. In this section, I just focus on the definitions and give examples where the normality ordering seems uncontroversial; I return to this issue in Chapter 4. I will point out for now that there are already subjective features in a model: the choice of variables and which variables are taken to be exogenous and endogenous is also determined by the modeler.
I now extend causal models to provide a formal model of normality. I do so by assuming that there is a partial preorder ⪰ over worlds. Intuitively, s ⪰ s′ means that s is at least as normal as s′. Recall from Section 2.1 that a partial order on a set S is a reflexive, anti-symmetric, and transitive relation on S. A partial preorder is reflexive and transitive but not necessarily anti-symmetric; this means that we can have two worlds s and s′ such that s ⪰ s′ and s′⪰ s without having s = s′. That is, we can have two distinct worlds where each is at least as normal as the other. By way of contrast, the standard ordering ≥ on the natural numbers is anti-symmetric; if x ≥ y and y ≥ x, then x = y. (The requirement of anti- symmetry is what distinguishes a (total or partial) order from a preorder.) I write s ≻ s′ if s ⪰ s′ and it is not the case that s′⪰ s, and s ≡ s′ if s ⪰ s′ and s′⪰ s. Thus, s ≻ s′ means that s is strictly more normal than s′, whereas s ≡ s′ means that s and s′ are equally normal. Note that I am not assuming that ⪰ is total; it is quite possible that there are two worlds s and s′ that are incomparable in terms of normality. The fact that s and s′ are incomparable does not mean that s and s′ are equally normal. We can interpret it as saying that the agent is not prepared to declare either s or s′ as more normal than the other and also not prepared to say that they are equally normal; they simply cannot be compared in terms of normality.
Recall that normality can be interpreted in terms of frequency. Thus, we say that birds typically fly in part because the fraction of flying birds is much higher than the fraction of non-flying birds. We might consider a world where a bird can fly to be more normal than one where a bird cannot fly. If we were to put a probability on worlds, then a world where a bird flies might well have a greater probability than one where a bird does not fly. Although we could interpret s ≻ s′ as meaning “s is more probable than s′”, this interpretation is not always appropriate. For one thing, interpreting ⪰ in terms of probability would make ⪰ a total order—all worlds would be comparable. There are advantages to allowing ⪰ to be partial (see the notes at the end of the chapter for more discussion of this point). More importantly, even when thinking probabilistically, I view s ≻ s′ as saying that s is much more probable than s′. I return to this point below.
Take an extended causal model to be a tuple ![[image]](images/ddcleq0862.jpg) , where
, where ![[image]](images/ddcleq0863.jpg) is a causal model and ⪰ is a partial preorder on worlds, which can be used to compare how normal different worlds are. In particular, ⪰ can be used to compare the actual world to a world where some interventions have been made. Which world is the actual world? That depends on the context. In a recursive extended causal model, a context
is a causal model and ⪰ is a partial preorder on worlds, which can be used to compare how normal different worlds are. In particular, ⪰ can be used to compare the actual world to a world where some interventions have been made. Which world is the actual world? That depends on the context. In a recursive extended causal model, a context ![[image]](images/ddcleq0864.jpg) determines a world denoted
determines a world denoted ![[image]](images/ddcleq0865.jpg) . We can think of the world
. We can think of the world ![[image]](images/ddcleq0866.jpg) as the actual world in context
as the actual world in context ![[image]](images/ddcleq0867.jpg) ; it is the world that would occur given the setting of the exogenous variables in
; it is the world that would occur given the setting of the exogenous variables in ![[image]](images/ddcleq0868.jpg) , provided that there are no external interventions.
, provided that there are no external interventions.
I now modify the HP definitions slightly to take the ordering of worlds into account. I start with the original and updated definitions. In this case, define ![[image]](images/ddcleq0869.jpg) to be a cause of φ in an extended model M and context
to be a cause of φ in an extended model M and context ![[image]](images/ddcleq0870.jpg) if
if ![[image]](images/ddcleq0871.jpg) is a cause of φ according to Definition 2.2.1, except that in AC2(a), a clause is added requiring that
is a cause of φ according to Definition 2.2.1, except that in AC2(a), a clause is added requiring that ![[image]](images/ddcleq0872.jpg) , where
, where ![[image]](images/ddcleq0873.jpg) is the world that results by setting
is the world that results by setting ![[image]](images/ddcleq0874.jpg) to
to ![[image]](images/ddcleq0875.jpg) and
and ![[image]](images/ddcleq0876.jpg) to
to ![[image]](images/ddcleq0877.jpg) in context
in context ![[image]](images/ddcleq0878.jpg) . This just says that we require the witness world to be at least as normal as the actual world. Here is the extended AC2(a), which I denote AC2+(a).
. This just says that we require the witness world to be at least as normal as the actual world. Here is the extended AC2(a), which I denote AC2+(a).
AC2+(a). There is a partition of ![[image]](images/ddcleq0879.jpg) (the set of endogenous variables) into two disjoint subsets
(the set of endogenous variables) into two disjoint subsets ![[image]](images/ddcleq0880.jpg) and
and ![[image]](images/ddcleq0881.jpg) with
with ![[image]](images/ddcleq0882.jpg) and a setting
and a setting ![[image]](images/ddcleq0883.jpg) and
and ![[image]](images/ddcleq0884.jpg) of the variables in
of the variables in ![[image]](images/ddcleq0885.jpg) and
and ![[image]](images/ddcleq0886.jpg) , respectively, such that
, respectively, such that ![[image]](images/ddcleq0887.jpg) and
and ![[image]](images/ddcleq0888.jpg) .
.
This can be viewed as a formalization of Kahneman and Miller’s observation that we tend to consider only possibilities that result from altering atypical features of a world to make them more typical, rather than vice versa. In this formulation, worlds that result from interventions on the actual world “come into play” in AC2+(a) only if they are at least as normal as the actual world. If we are using the modified HP definition, then AC2(am) is extended to AC2+(am) in exactly the same way; the only difference between AC2+(a) and AC2+(am) is that, in the latter (just as in AC2(am)), ![[image]](images/ddcleq0889.jpg) is required to consist of the values of the variables in
is required to consist of the values of the variables in ![[image]](images/ddcleq0890.jpg) in the actual context (i.e.,
in the actual context (i.e., ![[image]](images/ddcleq0891.jpg) ).
).
Issues of normality are, by and large, orthogonal to the differences between the variants of the HP definition. For ease of exposition, in the remainder of this chapter, I use the updated HP definition and AC+(a), unless noted otherwise. Using AC2+(a) rather than AC2(a), with reasonable assumptions about normality, takes care of the problems pointed out in Section 2, although it raises other issues.
Example 3.2.1 As I observed, one way to avoid calling the presence of oxygen a cause of the forest burning is simply not to include a variable for oxygen in the model or to take the presence of oxygen to be exogenous. But suppose someone wanted to consider oxygen to be an endogenous variable. Then as long as a world where there is no oxygen is more abnormal than a world where there is oxygen, the presence of oxygen is not a cause of the forest fire; AC2+(a) fails.
However, suppose that the fire occurs when a lit match is dropped in a special chamber in a scientific laboratory that is normally voided of oxygen. Then there would presumably be a different normality ordering. Now the presence of oxygen is atypical, and the witness to oxygen being a cause is as normal as (or at least not strictly less normal than) the witness to the match being a cause. In this case, I suspect most people would call the presence of oxygen a cause of the fire. ■
Example 3.2.2 Recall Example 2.3.5, where there are potentially many doctors who could treat Billy besides his regular doctor. Although it seems reasonable to call Billy’s regular doctor a cause of him being sick on Tuesday if the doctor fails to treat him, it does not seem reasonable to call all the other doctors causes of him being sick. This is easy to deal with if we take normality into account. It seems perfectly reasonable to take the world where Billy’s doctor treats Billy to be at least as normal as the world where Billy’s doctor does not treat Billy; it also seems reasonable to take the worlds where the other doctors treat Billy as being less normal than the world where they do not treat Billy. With these assumptions, using AC2+(a), Billy’s doctor not treating Billy is a cause of him being sick, whereas the other doctors not treating him are not causes. Thus, using normality allows us to capture intuitions that people seem to have without appealing to probabilistic sufficient causality and thus requiring a probability on contexts (see, for comparison, the discussion in Section 2.6).
What justifies a normality ordering where it is more normal for Billy’s doctor to treat him than another random doctor? All the interpretations discussed in Section 3.1 lead to this judgment.
There are philosophers who claim that an omission—the event of an agent not doing something—can never count as a cause. Although I do not share this viewpoint, it can be accommodated in this framework by taking not acting to always be more normal than acting. That is, given two worlds s and s′ that agree in all respects (i.e., in the values of all variables) except that in s some agents do not perform an act that they do perform in s′, we would have s ≻ s′. (As an aside, since ⪰ is allowed to be partial, if different agents perform acts in s and s′, then we can just take s and s′ to be incomparable.)
We can equally well accommodate a viewpoint that allows all omissions to count as causes. This is essentially the viewpoint of the basic HP definition, and we can recover the original HP approach (without normality), and hence drop the distinctions between omissions and other potential causes, by simply taking all worlds to be equally normal. (Indeed, by doing this, we are effectively removing normality from the picture and are back at the original HP definition.)
Of course, the fact that we can accommodate all these viewpoints by choosing an appropriate normality ordering raises the concern that we can reverse-engineer practically any verdict about causality in this way. Although it is true that adding normality to the model gives a modeler a great deal of flexibility, the key word here is “appropriate”. A modeler will need to argue that the normality ordering that she has chosen is reasonable and appropriate to capture the intuitions we have about the situation being modeled. Although there can certainly be some disagreement about what counts as “reasonable”, the modeler does not have a blank check here. I return to this issue in Section 4.7. ■
These examples already show that, once we take normality into account, causality ascriptions can change significantly. One consequence of this is that but-for causes may no longer be causes (according to all of the variants of the HP definition). The presence of oxygen is clearly a but-for cause of fire—if there is no oxygen, there cannot be a fire. But in situations where we take the presence of oxygen for granted, we do not want to call the presence of oxygen a cause.
Moreover, although it is still the case that a cause according to the updated HP definition is a cause according to the original HP definition, the other parts of Theorem 2.2.3 fail once we take normality into account.
Example 3.2.3 Suppose that two people vote in favor of a particular outcome and it takes two votes to win. Each is a but-for cause of the outcome, so all the definitions declare each voter to be a cause. But now suppose that we take the normality ordering to be such that it is abnormal for the two voters to vote differently, so a world where one voter votes in favor and the other votes against is less normal than a world where both vote in favor or both vote against. Taking V1 and V2 the variables describing how the voters vote, and O to describe the outcome, then with this normality ordering, neither V1 = 1 nor V2 = 1 is a cause of the outcome according to any of the variants of the HP definition, although V1 = 1 ∧ V2 = 1 is a cause. So, in particular, this means that causes are not necessarily single conjuncts according to the original HP definition once it is extended to take normality into account. Moreover, if the world where V1 = V2 = 0 is also taken to be abnormal, there is no cause at all of O = 1. ■
The fact that there are no causes in this case may not seem so unreasonable. With this normality setting, the outcome is essentially being viewed as a foregone conclusion and thus not in need of a cause. But there are other cases where having no causes seems quite unreasonable.
Example 3.2.4 Suppose that Billy is sick, Billy’s regular doctor treats Billy, and Billy recovers the next day. In this case, we would surely want to say that the fact that Billy’s doctor treated Billy is a cause of Billy recovering the next day. Indeed, it is even a but-for cause of Billy recovering. But if we assume that it is more normal for Billy’s regular doctor to treat Billy when he is sick than not to treat him, then taking normality into account, there is no cause of Billy recovering! It is easy to construct many other examples where there are no causes if the normal thing happens (a gardener watering her plants is not a cause of the plants surviving; if I normally drive home, then the fact that I drove home is not a cause of me being at home 20 minutes after I left work; and so on). This problem is dealt by the graded causality approach discussed in Section 3.3. ■
Example 3.2.5 Consider Example 2.9.1 again, where there is lightning and two arsonists. As we observed, the lightning is no longer a cause of the forest fire according to the modified HP definition, since each arsonist by himself is a cause. But suppose that we take a world where MD ≠ MD′ to be abnormal. This is consistent with the story, which says that one arsonist dropping a match “does not happen under normal circumstances”; in particular, MD ≠ MD′ is inconsistent with the equations. In that case, neither MD = 1 nor MD′ = 1 is a cause of FF = 1 according to modified HP definition in the extended causal model; neither satisfies AC2+(am). Thus, L = 1 ∧ MD = 1 becomes a cause of FF = 1 according to modified HP definition, and L = 1 is again part of a cause of FF = 1. ■
Example 3.2.6 Consider the sophisticated model ![[image]](images/ddcleq0892.jpg) of the rock-throwing example, and suppose that we declare the world where Billy throws a rock, Suzy doesn’t throw, and Billy does not hit abnormal. This world was needed to show that Suzy throwing is a cause according to the modified HP definition. Thus, with this normality ordering ST = 1 is not a cause; rather, ST = 1 BT = 1 is a cause, which seems inappropriate. However, ST = 1 remains a cause according to the original and updated HP definition, since we can now take the witness to be the world where ST = 0 and BT = 0; these variants allow the variables in
of the rock-throwing example, and suppose that we declare the world where Billy throws a rock, Suzy doesn’t throw, and Billy does not hit abnormal. This world was needed to show that Suzy throwing is a cause according to the modified HP definition. Thus, with this normality ordering ST = 1 is not a cause; rather, ST = 1 BT = 1 is a cause, which seems inappropriate. However, ST = 1 remains a cause according to the original and updated HP definition, since we can now take the witness to be the world where ST = 0 and BT = 0; these variants allow the variables in ![[image]](images/ddcleq0893.jpg) to take on values other than their values in the actual world. Thus, BT = 1 is part of a cause according to the modified HP definition but not a cause according to the original or updated HP definition. ■
to take on values other than their values in the actual world. Thus, BT = 1 is part of a cause according to the modified HP definition but not a cause according to the original or updated HP definition. ■
Example 3.2.6 shows in part why the normality ordering is placed on worlds, which are assignments of values to the endogenous variables only. The witness world where BT = 1, BH = 0, and ST = 0 does not seem so abnormal, even if it is abnormal for Billy to throw and miss in a context where he is presumed accurate.
Putting the normality ordering on worlds does not completely save the day, however. For one thing, it seems somewhat disconcerting that Billy’s throw should be part of the cause according to the modified HP definition in Example 3.2.6. But things get even worse. Suppose that we consider the richer model rock-throwing model ![[image]](images/ddcleq0894.jpg) , which includes the variable BA, for “Billy is an accurate rock thrower”. In
, which includes the variable BA, for “Billy is an accurate rock thrower”. In ![[image]](images/ddcleq0895.jpg) , we have essentially moved the question of Billy’s accuracy out of the context and made it an explicit endogenous variable, that is, it is determined by the world. In the actual world, Billy is accurate; that is, BA = 1. (Note that we may even have observations confirming this; we could see Billy’s rock passing right over where the bottle was just after Suzy’s rock hit it and shattered it.) There is still no problem here for the original and updated HP definition. If s is the actual world, then the world sBT=0,ST=0,u is arguably at least as normal as su; although BA = 1 in sBT=0,ST=0,u, it is not abnormal for Billy not to hit the bottle if he doesn’t throw. On the other hand, in the world sBH =0,ST=0,u which is needed to show that Suzy’s throw is a cause of the bottle shattering according to the modified HP definition, we have BT = 1, BA = 1, and BH = 0: although Billy throws and is accurate, he misses the bottle. This doesn’t seem like such a normal world. But if we declare this world to be abnormal, then Suzy’s throw is no longer a cause of the bottle shattering according to the modified HP definition.
, we have essentially moved the question of Billy’s accuracy out of the context and made it an explicit endogenous variable, that is, it is determined by the world. In the actual world, Billy is accurate; that is, BA = 1. (Note that we may even have observations confirming this; we could see Billy’s rock passing right over where the bottle was just after Suzy’s rock hit it and shattered it.) There is still no problem here for the original and updated HP definition. If s is the actual world, then the world sBT=0,ST=0,u is arguably at least as normal as su; although BA = 1 in sBT=0,ST=0,u, it is not abnormal for Billy not to hit the bottle if he doesn’t throw. On the other hand, in the world sBH =0,ST=0,u which is needed to show that Suzy’s throw is a cause of the bottle shattering according to the modified HP definition, we have BT = 1, BA = 1, and BH = 0: although Billy throws and is accurate, he misses the bottle. This doesn’t seem like such a normal world. But if we declare this world to be abnormal, then Suzy’s throw is no longer a cause of the bottle shattering according to the modified HP definition.
It gets even worse (at least according to some people’s judgments of causality) if we replace Billy the person by Billy the automatic rock-throwing machine, which is programmed to throw rocks. Again, it does not seem so bad if BA is not part of the language; programming errors or other malfunctions can still result in a rock-throwing machine missing. But with BA in the language (in which case we take BA = 1 to mean that the machine doesn’t malfunction and is programmed correctly), it does not seem so reasonable to take a world where BA = 1, BT = 1, and BH = 0 to be at least as normal as the actual world.
Does this represent a serious problem for the modified HP definition (when combined with normality)? I would argue that, although at first it may seem reasonable (and is what was done in the literature), the real source of the problem is putting normality on worlds. I return to this point in Section 3.5, where I consider an alternative approach to defining normality. For now I continue with putting normality on worlds and consider an approach that deals with the problem in the rock-throwing example in a different way, which has the further advantage of providing a more general approach to combining normality with causality.
AC2+(a) and AC2+(am), as stated, are all-or-nothing conditions; either it is legitimate to consider a particular world (the one that characterizes the witness) or it is not. However, in some cases, to show that A is a cause of B, we might need to consider an unlikely intervention; it is the only one available. This is exactly what happened in the case of the rock-throwing machine.
As observed in Examples 3.2.3 and 3.2.4, with certain normality orderings, some events can have no cause at all (although they would have a cause if normality constraints were ignored). We can avoid this problem by using normality to rank actual causes, rather than eliminating them altogether. Doing so lets us explain the responses that people make to queries regarding actual causation. For example, while counterfactual approaches to causation usually yield multiple causes of an outcome φ, people typically mention only one of them when asked for a cause. One explanation of this is that they are picking the best cause, where best is judged in terms of normality.
To make this precise, say that world s is a witness world (or just witness) for ![[image]](images/ddcleq0896.jpg) being a cause of φ in context
being a cause of φ in context ![[image]](images/ddcleq0897.jpg) if for some choice of
if for some choice of ![[image]](images/ddcleq0898.jpg) ,
, ![[image]](images/ddcleq0899.jpg) , and
, and ![[image]](images/ddcleq0900.jpg) for which AC2(a) and AC2(bu) hold (AC2(a) and AC2(bo) if we are using the original HP definition; AC2(am) if we are using the modified HP definition), s is the assignment of values to the endogenous variables that results from setting
for which AC2(a) and AC2(bu) hold (AC2(a) and AC2(bo) if we are using the original HP definition; AC2(am) if we are using the modified HP definition), s is the assignment of values to the endogenous variables that results from setting ![[image]](images/ddcleq0901.jpg) and
and ![[image]](images/ddcleq0902.jpg) in context
in context ![[image]](images/ddcleq0903.jpg) . In other words, a witness s is a world that demonstrates that AC2(a) holds. (Calling a world s a witness world is consistent with calling the triple
. In other words, a witness s is a world that demonstrates that AC2(a) holds. (Calling a world s a witness world is consistent with calling the triple ![[image]](images/ddcleq0904.jpg) a witness, as I did in Section 2.2. The triple determines a unique world, which is a witness world. I continue to use the word “witness” for both a witness world and a triple. I hope that the context will make clear which is meant.)
a witness, as I did in Section 2.2. The triple determines a unique world, which is a witness world. I continue to use the word “witness” for both a witness world and a triple. I hope that the context will make clear which is meant.)
In general, there may be many witness worlds for ![[image]](images/ddcleq0905.jpg) being a cause of φ in
being a cause of φ in ![[image]](images/ddcleq0906.jpg) . Say that s is a best witness for
. Say that s is a best witness for ![[image]](images/ddcleq0907.jpg) being a cause of φ if there is no other witness s′ such that s′ ≻ s. (Note that there may be more than one best witness.) We can then grade candidate causes according to the normality of their best witnesses. We would expect that someone’s willingness to judge
being a cause of φ if there is no other witness s′ such that s′ ≻ s. (Note that there may be more than one best witness.) We can then grade candidate causes according to the normality of their best witnesses. We would expect that someone’s willingness to judge ![[image]](images/ddcleq0908.jpg) an actual cause of φ in
an actual cause of φ in ![[image]](images/ddcleq0909.jpg) increases as a function of the normality of the best witness world for
increases as a function of the normality of the best witness world for ![[image]](images/ddcleq0910.jpg) in comparison to the best witness for other candidate causes. Thus, we are less inclined to judge that
in comparison to the best witness for other candidate causes. Thus, we are less inclined to judge that ![[image]](images/ddcleq0911.jpg) is an actual cause of φ when there are other candidate causes with more normal witnesses.
is an actual cause of φ when there are other candidate causes with more normal witnesses.
Note that once we allow graded causality, we use AC2(a) (resp., AC2(am)) rather than AC2+(a) (resp., AC2+(am)); normality is used only to characterize causes as “good” or “poor”. In Example 3.2.2, each doctor other than Billy’s doctor not treating Billy is still a cause of Billy being sick on Tuesday, but is such a poor cause that most people are inclined to ignore it if there is a better cause available. On the other hand, in Example 3.2.4, Billy’s doctor treating Billy is a cause of Billy recovering the next day, and is the only cause, so it is what we take as “the” cause. In general, an event whose only causes are poor causes in this sense is one that we expected all along, so doesn’t require an explanation (see Example 3.4.1). However, if we are looking for a cause, then even a poor cause is better than nothing.
Before going on, I should note that it has been common in the philosophy literature on causation to argue that, although people do seem to grade causality, it is a mistake to do so (see the notes for more discusion on this point). As I said, one of my goals is to get a notion of causality that matches how people use the word and is useful. Since it is clear that people make these distinctions, I think it is important to get a reasonable definition of causality that allows the distinctions to be made. Moreover, I think that people make these distinctions because they are useful ones. Part of why we want to ascribe causality is to understand how to solve problems. We might well want to understand why Billy’s doctor did not treat Billy. We would not feel the need to understand why other doctors did not treat Billy.
In this section, I give a few more examples showing the power of adding normality to the definition of causality and the advantages of thinking in terms of graded causality.
Recall the vignette from Knobe and Fraser’s experiment that was discussed in Section 3.1, where Professor Smith and the administrative assistant both take pens from the receptionist’s desk. After reading this vignette, subjects were randomly presented with one of the following propositions and asked to rank their agreement on a 7-point scale from -3 (completely disagree) to +3 (completely agree):
Professor Smith caused the problem.
The administrative assistant caused the problem.
Subjects gave an average rating of 2.2 to the first claim, indicating agreement, but −1.2 to the second claim, indicating disagreement. Thus, subjects are judging the two claims differently, due to the different normative status of the two actions. (Note that subjects were only presented with one of these claims: they were not given a forced choice between the two.)
In another experiment, subjects were presented with a similar vignette, but this time both professors and administrative assistants were allowed to take pens. In this case, subjects tend to give intermediate values. That is, when the vignette is changed so that Professor Smith is not violating a norm when he takes the pen, not only are subjects less inclined to judge that Professor Smith caused the problem, but they are more inclined to judge that the administrative assistant caused the problem. The most plausible interpretation of these judgments is that subjects’ increased willingness to say that the administrative assistant caused the problem is a direct result of their decreased willingness to say that Professor Smith caused the problem. This suggests that attributions of actual causation are at least partly a comparative affair.
The obvious causal model of the original vignette has three endogenous variables:
There is one equation: PO = min(PT, AT) (equivalently, PO = PT ∧ AT). The exogenous variables are such that PT and AT are both 1. Therefore, in the actual world, we have PT = 1, AT = 1, and PO = 1.
Both PT = 1 and AT = 1 are but-for causes of PO = 1 (and so causes according to all three variants of the definition). The best witness for PT = 1 being a cause is the world (PT = 0, AT = 1, PO = 0); the best witness for AT = 1 being a cause is (PT = 1, AT = 0, PO = 0). (Here and elsewhere, I describe a world by a tuple consisting of the values of the endogenous variables in that world.) The original story suggests that the witness for PT = 1 being a cause is more normal than the witness for AT = 1 by saying “administrative assistants are allowed to take pens, but professors are supposed to buy their own”. According to the definition above, this means that people are more likely to judge that PT = 1 is an actual cause. However, if the vignette does not specify that one of the actions violates a norm, we would expect the relative normality of the two witnesses to be much closer, which is reflected in how subjects actually rated the causes.
This example, I believe, illustrates the power of allowing a “graded” approach to causality. As I said above, there have been claims that it is a mistake to focus on one cause and ignore others (which is an extreme of the graded approach that occurs often in practice). It seems to me that the “egalitarian” notion of cause is entirely appropriate at the level of causal structure, as represented by the equations of a causal model. These equations represent arguably objective features of the world and are not sensitive to factors such as contextual salience and human considerations of normality. Pragmatic, subjective factors then determine which actual causes we select and label “the” causes (or, at least, as “better” causes).
The initial impetus for work on adding normality considerations to basic causal models was provided by the examples like the following “bogus prevention” example.
Example 3.4.1 Assassin is in possession of a lethal poison but has a last-minute change of heart and refrains from putting it in Victim’s coffee. Bodyguard puts antidote in the coffee, which would have neutralized the poison had there been any. Victim drinks the coffee and survives. Is Bodyguard’s putting in the antidote a cause of Victim surviving? Most people would say no, but according to the original and updated HP definition, it is. For in the contingency where Assassin puts in the poison, Victim survives iff Bodyguard puts in the antidote. According to the modified HP definition, Bodyguard putting in the antidote is not a cause, but is part of a cause (along with Assassin not putting in the poison). Although the latter position is perhaps not completely unreasonable (after all, if Bodyguard didn’t put in the antidote and Assassin did put in the poison, Victim would have died), most people would not take either Bodyguard or Assassin to be causes. Roughly speaking, they would reason that there is no need to find a cause for something that was expected all along. ■
What seems to make Example 3.4.1 particularly problematic is that, if we use the obvious variables to describe the problem, the resulting structural equations are isomorphic to those in the disjunctive version of the forest-fire example where either the lit match or the lightning suffices to start the fire. Specifically, take the endogenous variables in Example 3.4.1 to be A (for “assassin does not put in poison”), B (for “bodyguard puts in antidote”), and VS (for “victim survives”). That is,
Then A, B, and VS satisfy exactly the same equations as L, MD, and FF, respectively: A and B are determined by the environment, and VS = A ∨ B. In the context where there is lightning and the arsonist drops a lit match, both the lightning and the match are causes of the forest fire according to the original and updated HP definition (and parts of causes according to the modified HP definition), which seems reasonable. For similar reasons, in this model, the original and updated HP definition declare both A = 1 and B = 1 to be causes of VS = 1 (and the modified HP definition declares them to be parts of causes). But here it does not seem reasonable that Bodyguard’s putting in the antidote is a cause or even part of a cause. Nevertheless, it seems that any definition that just depends on the structural equations is bound to give the same answers in these two examples.
Using normality gives us a straightforward way of dealing with the problem. In the actual world, A = 1, B = 1, and VS = 1. The witness world for B = 1 being a cause of VS = 1 is the world where A = 0, B = 0, and VS = 0. If we make the assumption that A is typically 1 and that B is typically 0, this leads to a normality ordering in which the two worlds (A = 1, B = 1, VS = 1) and (A = 0, B = 0, VS = 0) are incomparable; although both are abnormal, they are abnormal in incomparable ways. Since the unique witness for B = 1 to be an actual cause of VS = 1 is incomparable with the actual world, using AC2+(a), we get that B = 1 is not an actual cause of VS = 1.
Note that if we require AC2+(a), A = 1 is not a cause of VS = 1 either; the world (A = 0, B = 0, VS = 0) is also the unique witness world for A = 1 being a cause of VS = 1. That means VS = 1 has no causes. Again, in this case, we would typically not look for an explanation or a cause of VS = 1 because it was expected all along. However, if we are looking for a cause, using graded causality, both A = 1 and B = 1 count as causes of VS = 1 according to the original and updated HP definition (extended to take normality into account, of course), although they get a “poor” grade; with the modified HP definition, the conjunction A = 1 B = 1 counts as a cause. Again, we are inclined to accept a “poor” cause as a cause if there are no better alternatives available.
Now suppose that we consider a world where assassination is typical; assassins are hiding behind every corner. Would we then want to take worlds where A = 0 to be more normal than worlds where A = 1, all else being fixed? Indeed, even if assassinations were not common-place, isn’t it typical for assassins to poison drinks? That is what assassins do, after all. Here we are dealing with two different interpretations of “normality”. Even if assassinations occur frequently, they are morally wrong, and hence abnormal in the moral sense. Still, perhaps we would be more willing to accept the assassin not putting in poison as a cause of the victim surviving in that case; we certainly wouldn’t take VS = 1 to be an event that no longer requires explanation. Indeed, imagine the assassin master sent his crack assassin out to murder the victim and then discovers that the victim is still alive. Now he would want an explanation, and the explanation that the assassin did not actually put in the poison now seems more reasonable.
Although (despite the caveats just raised) using normality seems to deal with the assassin problem, there is another, arguably better, way of modeling this example that avoids issues of normality altogether. The idea is similar in spirit with how the rock-throwing problem was handled. We add a variable PN to the model, representing whether a chemical reaction takes place in which poison is neutralized. Of course PN = 1 exactly if the assassin puts in the poison and Bodyguard adds the antidote. Thus, the model has the following two equations:
Thus, in the actual world, where A = 1 and B = 1, PN = 0. The poison is not neutralized because there was never poison there in the first place. With the addition of PN, B = 1 is no longer a cause of VS = 1 according to the original or updated HP definitions, without taking normality into account. Clearly, if B = 1 were to be a cause, the set ![[image]](images/ddcleq0912.jpg) would have to include A, and we would have to set A = 0. The question is whether PN is in
would have to include A, and we would have to set A = 0. The question is whether PN is in ![[image]](images/ddcleq0913.jpg) or
or ![[image]](images/ddcleq0914.jpg) . Either way, AC2(bo) would not hold. For if
. Either way, AC2(bo) would not hold. For if ![[image]](images/ddcleq0915.jpg) , then since its original value is 0, if A is set to 0 and PN is set to its original value of 0, then VS = 0 even if B = 1. In contrast, if
, then since its original value is 0, if A is set to 0 and PN is set to its original value of 0, then VS = 0 even if B = 1. In contrast, if ![[image]](images/ddcleq0916.jpg) , we must set PN = 0 for AC2(a) to hold, and with this setting, AC2(bo) again does not hold.
, we must set PN = 0 for AC2(a) to hold, and with this setting, AC2(bo) again does not hold.
However, A = 1 is a cause of VS = 1, according to all variants of the HP definition. (If we fix PN at its actual value of 0 and set A = 0, then VS = 0.) It follows that B = 1 is not even part of a cause of VS = 1 according to the modified HP definition. (This also follows from Theorem 2.2.3.) Although it seems reasonable that B = 1 should not be a cause of VS = 1, is it reasonable that A = 1 should be a cause? Anecdotally, most people seem to find that less objectionable than B = 1 being a cause. Normality considerations help explain why people are not so enthusiastic about calling A = 1 a cause either, although it is a “better” cause than B = 1.
Interestingly, historically, this example was the motivation for introducing normality considerations. Although normality is perhaps not so necessary to deal with it, it does prove useful in a small variant of this example.
Example 3.4.2 Again, suppose that Bodyguard puts an antidote in Victim’s coffee, but now Assassin puts the poison in the coffee. However, Assassin would not have put the poison in the coffee if Bodyguard hadn’t put the antidote in. (Perhaps Assassin is putting in the poison only to make Bodyguard look good.) Formally, we have the equation A = ¬B. Now Victim drinks the coffee and survives.
Is Bodyguard putting in the antidote a cause of Victim surviving? It is easy to see that, according to all three variants of the HP definition, it is. If we fix A = 0 (its value in the actual world), then Victim survives if and only if Bodyguard puts in the antidote. Intuition suggests that this is unreasonable. By putting in the antidote, Bodyguard neutralizes the effect of the other causal path he sets in action: Assassin putting in the poison.
Here normality considerations prove quite useful. The world where Bodyguard doesn’t put in the antidote but Assassin puts in the poison anyway (i.e., A = B = 0) directly contradicts the story. Given the story, this world should be viewed as being less normal than the actual world, where A = 0 and B = 1. Thus, B = 1 is not a cause of V = 1 in the extended model, as we would expect. ■
As the following example shows, normality considerations do not solve all problems.
Example 3.4.3 Consider the train in Example 2.3.6 that can go on different tracks to reach the station. As we observed, if we model the story using only the variables F (for “flip”) and T (for “track”), then flipping the switch is not a cause of the train arriving at the station. But if we add variables LB and RB (for left-hand track blocked and right-hand track blocked, with LB = RB = 0 in the actual context), then it is, according to the original and updated HP definition, although not according to the modified HP definition. Most people would not consider the flip a cause of the train arriving. We can get this outcome even with the original and updated definition if we take normality into account. Specifically, suppose that the train was originally going to take the left track and took the right track as a result of the switch. To show that the switch is a cause, consider the witness world where LB = 1 (and RB = 0). If we assume, quite reasonably, that this world is less normal than the actual world, where LB = RB = 0, then flipping the switch no longer counts as a cause, even with the original and updated HP definition.
But normality doesn’t quite save the day here. Suppose that we consider the context where both tracks are blocked. In this case, the original and updated HP definitions declare the flip a cause of the train not arriving (by considering the contingency where LB = 0). Normality considerations don’t help; the contingency where LB = 0 is more normal than the actual situation, where the track is blocked. The modified definition again matches intuitions better; it does not declare flipping the switch a cause.
As pointed out in the notes to Chapter 2, there is yet another way of modeling the story. Instead of the variables LB and RB, we use the variables LT (“train went on the left track”) and RT (“train went on the right track”). In the actual world, F = 1, RT = 1, LT = 0, and A = 1. Now F = 1 is a cause of A = 1, according to all the variants of the HP definition. If we simply fix LT = 0 and set F = 0, then A = 0. But in this case, normality conditions do apply: the world where the train does not go on the left track despite the switch being set to the left is less normal than the actual world. ■
Voting can lead to some apparently unreasonable causal outcomes (at least, if we model things naively). Consider Jack and Jill, who live in an overwhelmingly Republican district. As expected, the Republican candidate wins with an overwhelming majority. Jill would normally have voted Democrat but did not vote because she was disgusted by the process. Jack would normally have voted Republican but did not vote because he (correctly) assumed that his vote would not affect the outcome. In the naive model, both Jack and Jill are causes of the Republican victory according to all the variants of the HP definition. For if enough of the people who voted Republican had switched to voting Democrat or abstaining, then if Jack (or Jill) had voted Democrat, the Democrat would have won or it would have been a tie, whereas the Republican would have won had they abstained.
We can do better by constructing a model that takes these preferences into account. One way to do so is to assume that their preferences are so strong that we may as well take them for granted. Thus, the preferences become exogenous; the only endogenous variables are whether they vote (and the outcome); if they vote at all, they vote according to their preferences. In this case, Jack’s not voting is not a cause of the outcome, but Jill’s not voting is.
More generally, with this approach, the abstention of a voter whose preference is made exogenous and is a strong supporter of the victor does not count as a cause of victory. This does not seem so unreasonable. After all, in an analysis of a close political victory in Congress, when an analyst talks about the cause(s) of victory, she points to the swing voters who voted one way or the other, not the voters who were taken to be staunch supporters of one particular side.
That said, making a variable exogenous seems like a somewhat draconian solution to the problem. It also does not allow us to take into account smaller gradations in depth of feeling. At what point should a preference switch from being endogenous to exogenous? We can achieve the same effect in an arguably more natural way by using normality considerations. In the case of Jack and Jill, we can take voting for a Democrat to be highly abnormal for Jack and voting for a Republican to be highly abnormal for Jill. To show that Jack (resp., Jill) abstaining is a cause of the victory, we need to consider a contingency where Jack (resp., Jill) votes for the Democratic candidate. This would be a change to a highly abnormal world in the case of Jack but to a more normal world in the case of Jill. Thus, if we use normality as a criterion for determining causality, Jill would count as a cause, but Jack would not. If we use normality as a way of grading causes, Jack and Jill would still both count as causes for the victory, but Jill would be a much better cause. More generally, the more normal it would be for someone who abstains to vote Democrat, the better a cause that voter would be. The use of normality here allows for a more nuanced gradation of cause than the rather blunt approach of either making a variable exogenous or endogenous.
Now consider a vote where everyone can vote for one of three candidates. Suppose that the actual vote is 17–2–0 (i.e., 17 vote for candidate A, 2 for candidate B, and none for candidate C). Then not only is every vote for candidate A a cause of A winning, every vote for B is also a cause of A winning according to the original and updated HP definition. To see this, consider a contingency where 8 of the voters for A switch to C. Then if one of the voters for B votes for C, the result is a tie; if that voter switches back to B, then A wins (even if some subset of the voters who switch from A to C switch back to A). According to the modified HP definition, each voter for B is part of a cause of A’s victory. The argument is essentially the same: had a voter for B switched to C along with eight of the voters for A, it would have been a tie, so A would not have won.
Is this reasonable? What makes it seem particularly unreasonable is that if it had just been a contest between A and B, with the vote 17–2, then the voters for B would not have been causes of A winning. Why should adding a third option make a difference? Arguably, the modified HP definition makes it clear why adding the third option makes a difference: the third candidate could win according to the appropriate circumstances, and those circumstances include the voters for B changing their votes.
Indeed, it is clear that adding a third option can well make a difference in some cases. For example, we speak of Nader costing Gore a victory over Bush in the 2000 election. But we don’t speak of Gore costing Nader a victory, although in a naive HP model of the situation, all the voters for Gore are causes of Nader not winning as much as the voters for Nader are causes of Gore not winning. The discussion above points to a way out of this dilemma. If a sufficiently large proportion of Bush and Gore voters are taken to be such strong supporters that they will never change their minds, and we make their votes exogenous, then it is still the case that Nader caused Gore to lose (assuming that most Nader voters would have voted for Gore if Nader hadn’t run), but not the case that Gore caused Nader to lose. Similar considerations apply in the case of the 17–2 vote. And again, we can use normality considerations to give arguably more natural models of these examples. As we shall see in Chapter 6, using ideas of blame and responsibility give yet another approach to dealing with these concerns.
As I argued in Section 2.4, causation seems transitive when there is a simple causal chain involving but-for causality, and the final effect counterfactually depends on the initial cause. By contrast, the law does not assign causal responsibility for sufficiently remote consequences of an action. For example, in Regina v. Faulkner, a well-known Irish case, a lit match aboard a ship caused a cask of rum to ignite, causing the ship to burn, which resulted in a large financial loss by Lloyd’s insurance, leading to the suicide of a financially ruined insurance executive. The executive’s widow sued for compensation, and it was ruled that the negligent lighting of the match was not a cause (in the legally relevant sense) of his death. By taking normality into account, we can make sense of this kind of attenuation.
We can represent the case of Regina v. Faulkner using a causal model with nine variables:
There are four structural equations:
This model is shown graphically in Figure 3.1. The exogenous variables are such that M, R, F, LI, and EU are all 1, so in the actual world, all variables take the value 1. Intuitively, the events M = 1, RI = 1, SD = 1, LL = 1, and ES = 1 form a causal chain. The first four events are but-for causes of ES = 1, and so are causes according to all variants of the HP definition.
![[image]](images/fig3-1.jpg)
Figure 3.1: Attenuation in a causal chain.
Let us now assume that, for the variables M, R, F, LI, and EU, 0 is the typical value, and 1 is the atypical value. Consider a very simple normality ordering, which is such that worlds where more of these variables take the value 0 are more normal. For simplicity, consider just the first and last links in the chain of causal reasoning: LL = 1 and M = 1, respectively. The world w = (M = 0, R = 1, RI = 0, F = 1, SD = 0, LI = 1, LL = 0, EU = 1, ES = 0) is a witness of M = 1 being a cause of ES = 1 (for any of the variants of the HP definition). This is quite an abnormal world, although more normal than the actual world, so M = 1 does count as an actual cause of ES = 1, even using AC2+(a). However, note that if any of the variables R, F, LI, or EU is set to 0, then we no longer have a witness. Intuitively, ES counterfactually depends on M only when all of these other variables take the value 1. Now consider the event LL = 1. The world w′ = (M = 0, R = 0, RI = 0, F = 0, SD = 0, LI = 0, LL = 0, EU = 1, ES = 0) is a witness for LL = 1 being an actual cause of ES = 1 according to the original and updated HP definition. World w′ is significantly more normal than the best witness for M = 1 being a cause. Intuitively, LL = 1 needs fewer atypical conditions to be present in order to generate the outcome ES = 1. It requires only the instability of the executive, but not the presence of rum, other flammable materials, and so on. So although both LL = 1 and M = 1 count as causes using AC2+(a), LL = 1 is a better cause, so we would expect that people would be more strongly inclined to judge that LL = 1 is an actual cause of ES = 1 than M = 1.
Once we take normality into account, we can also have a failure of transitivity. For example, suppose that we slightly change the normality ordering so that the world w = (M = 0, R = 1, RI = 0, F = 1, SD = 0, LI = 1, LL = 0, EU = 1, ES = 0) that is a witness of M = 1 being a cause of ES = 1 is less normal than the actual world, but otherwise leave the normality ordering untouched. Now M = 1 is no longer a cause of ES = 1 using AC2+(a). However, causality still holds for each step in the chain: M = 1 is a cause of RI = 1, RI = 1 is a cause of SD = 1, SD = 1 is a cause of LL = 1, and LL = 1 is a cause of ES = 1. Thus, normality considerations can explain the lack of transitivity in long causal chains.
Note that the world w′ is not a witness according to the modified HP definition since, in w′, the values of the variables R, F, and LI differ from their actual values. Normality does not seem to help in this example if we use the modified HP definition. However, as we shall see in Section 6.2, we can deal with this example perfectly well using the modified HP definition if we use ideas of blame.
It is worth noting that, with the original and updated HP definition, the extent to which we have attenuation of actual causation over a causal chain is not just a function of the number of links in the chain. It is, rather, a function of how abnormal the circumstances are that must be in place in order for the causal chain to run from start to finish.
3.4.5 Legal doctrines of intervening causes
In general, the law holds that one is not causally responsible for some outcome that occurred only due to either a later deliberate action by some other agent or some very improbable event. For example, if Anne negligently spills gasoline, and Bob carelessly throws a cigarette into the spilled gasoline, then Anne’s action is a cause of the fire. But if Bob maliciously throws a cigarette into the spilled gasoline, then Anne is not considered a cause. (This example is based on the facts on an actual case: Watson v. Kentucky and Indiana Bridge and Railroad.) This kind of reasoning can also be modeled using an appropriate normality ordering, as I now show.
To fully capture the legal concepts, we need to represent the mental states of the agents. We can do this with the following six variables:
We have the following equations:
This model is shown graphically in Figure 3.2. (Note that the model incorporates certain assumptions about what happens in the case where Bob is both malicious and careless and in the cases where Anne does not spill gasoline; what happens in these cases is not clear from the usual description of the example. These assumptions do not affect the analysis.)
![[image]](images/fig3-2.jpg)
Figure 3.2: An intervening cause.
It seems reasonable to assume that BM, BC, and AN typically take the value 0. But more can be said. In the law, responsibility requires a mens rea—literally, a guilty mind. Mens rea comes in various degrees. Starting with an absence of mens rea and then in ascending order of culpability, these are:
We can represent this scale in terms of decreasing levels of typicality. Specifically, in decreasing order of typicality, we have
Thus, although “carelessness” is not on the scale, I have implicitly taken it to represent less culpability than negligence.
In all the examples up to now, I have not needed to compare worlds that differed in the value of several variables in terms of normality. Here, when comparing the normality of worlds in which two of these variables take the value 0 and one takes the value 1, we can capture legal practice by taking the world with BC = 1 to be most normal, the world with AN = 1 to be next most normal, and the world with BM = 1 to be least normal. Consider first the case where Bob is careless. Then in the actual world we have
![[image]](images/ddcleq0917.jpg)
In the structural equations, F = 1 depends counterfactually on both BC = 1 and AN = 1. Thus, these are both but-for causes, so are causes according to all the variants of the HP definition. The best witness for AN = 1 being a cause is
![[image]](images/ddcleq0918.jpg)
and the best witness for BC = 1 being a cause is
![[image]](images/ddcleq0919.jpg)
Both of these worlds are more normal than the actual world. The first is more normal because AN takes the value 0 instead of 1. The second world is more normal than the actual world because BC takes the value 0 instead of 1. Hence, according to AC2+(a), both are actual causes. However, the best witness for AN = 1 is more normal than the best witness for BC = 1. The former witness has BC = 1 and AN = 0, and the latter witness has BC = 0 and AN = 1. Since AN = 1 is more atypical than BC = 1, the first witness is more normal. This means that we are more inclined to judge Anne’s negligence a cause of the fire than Bob’s carelessness.
Now consider the case where Bob is malicious. The actual world is
![[image]](images/ddcleq0920.jpg)
Again, without taking normality into account, both BM = 1 and AN = 1 are actual causes. The best witness for AN = 1 being a cause is
![[image]](images/ddcleq0921.jpg)
and the best witness for BM = 1 is
![[image]](images/ddcleq0922.jpg)
However, now the best witness for AN = 1 is less normal than the best witness for BM = 1 because BM = 1 is more atypical than AN = 1. So using this normality ordering, we are more inclined to judge that Bob’s malice is an actual cause of the fire than that Anne’s negligence is.
Recall that in Example 3.4.1, judgments of the causal status of the administrative assistant’s action changed, depending on the normative status of the professor’s action. Something similar is happening here: the causal status of Anne’s action changes with the normative status of Bob’s action. This example also illustrates how context can play a role in determining what is normal and abnormal. In the legal context, there is a clear ranking of norm violations.
3.5 An Alternative Approach to Incorporating Normality
I now present an alternative approach to incorporating normality concerns in causal models, inspired by the discussion after Example 3.2.6. As suggested earlier, this approach is also more compatible with the way that probability was incorporated into causal models. The first step is to put the normality ordering on causal settings. Since, for the purposes of this discussion, the causal model is fixed, this amounts to putting a normality ordering on contexts, rather than on worlds. This means that normality can be viewed as a qualitative generalization of probability. But, as I suggested before, to the extent that we are thinking probabilistically, we should interpret ![[image]](images/ddcleq0923.jpg) as meaning “
as meaning “![[image]](images/ddcleq0924.jpg) is much more probable than
is much more probable than ![[image]](images/ddcleq0925.jpg) ”.
”.
Putting the normality ordering on contexts clearly does not by itself solve the problem. Indeed, as noted in the discussion immediately after Example 3.2.6, the motivation for putting the normality ordering on worlds rather than contexts was to solve problems that resulted from putting the normality ordering on context! There is an additional step: lifting the normality order on contexts to a normality ordering on sets of contexts. Again, this is an idea motivated by probability. We usually compare events, that is, sets of worlds, using probability, not just single worlds; I will also be comparing sets of contexts in the alternative approach to using normality.
When using probability (ignoring measurability concerns), the probability of a set is just the sum of the probabilities of the elements in the set. But with normality, “sum” is in general undefined. Nevertheless, we can lift a partial preorder on an arbitrary set S to a partial preorder on 2S (the set of subsets of S) in a straightforward way. Given sets A and B of contexts, say A ⪰e B if, for all contexts ![[image]](images/ddcleq0926.jpg) , there exists a context
, there exists a context ![[image]](images/ddcleq0927.jpg) such that
such that ![[image]](images/ddcleq0928.jpg) . (I use the superscript e to distinguish the order ⪰e on events—sets of contexts—from the underlying order ⪰ on contexts.) In words, this says that A is at least as normal as B if, for every context in B, there is a context in A that is at least as normal.
. (I use the superscript e to distinguish the order ⪰e on events—sets of contexts—from the underlying order ⪰ on contexts.) In words, this says that A is at least as normal as B if, for every context in B, there is a context in A that is at least as normal.
Clearly we have u ⪰ u′ iff {u} ⪰e {u}, so ⪰e extends ⪰ in the obvious sense. The definition of ⪰e has a particularly simple interpretation if ⪰ is a total preorder on contexts and A and B are finite. In that case, there is a most normal context uA in A (there may be several equally normal contexts in A that are most normal; in that case, let uA be one of them) and a most normal context uB in B. It is easy to see that A ⪰e B iff uA ⪰ uB. That is, A is at least as normal as B if the most normal worlds in A are at least as normal as the most normal worlds in B. Going back to probability, this says that the qualitative probability of an event is determined by its most probable element(s). For those familiar with ranking functions (see the notes at the end of the chapter), this ordering on events is exactly that determined by ranking functions.
Taking the causal model M to be fixed, let ⟦φ⟧ denote the event corresponding to a propositional formula φ; that is, ![[image]](images/ddcleq0929.jpg) is the set of contexts where φ is true. I now modify AC2+(a) and AC2(am) so that instead of requiring that
is the set of contexts where φ is true. I now modify AC2+(a) and AC2(am) so that instead of requiring that ![[image]](images/ddcleq0930.jpg) , I require that
, I require that ![[image]](images/ddcleq0931.jpg) ; that is, the set of worlds where the witness
; that is, the set of worlds where the witness ![[image]](images/ddcleq0932.jpg) holds is at least as likely as the set of worlds satisfying
holds is at least as likely as the set of worlds satisfying ![[image]](images/ddcleq0933.jpg) .
.
Doing this solves the problem in the rock-throwing example. For one thing, with this change, the addition of BA (the accuracy of Billy’s throw) to the language in the rock-throwing example has no impact. More generally, whether something like accuracy is modeled by an endogenous variable or an exogenous variable has no impact on normality considerations; in either case, we would still consider the same set of contexts when comparing the normality of ⟦BH = 0 ∧ ST = 0 ∧ BS = 0⟧ and ⟦ST = 1 ∧ BS = 1⟧. It seems reasonable to view BH = 0 ∧ ST = 0 ∧ BS = 0 as being relatively normal. Even if Billy typically throws and typically is an accurate shot, he does occasionally not throw or throw and miss. Thinking probabilistically, even if the probability of the event ⟦BH = 0 ∧ ST = 0 ∧ BS = 0⟧ is lower than that of ⟦ST = 1 ∧ BS = 1⟧, it is not sufficiently less probable to stop the former from being as normal as the latter. (Here I am applying the intuition that ≻ represents “much more probable than” rather than just “more probable than”.) This viewpoint makes sense even if Billy is replaced by a machine. Put another way, although it may be unlikely that the rock-throwing machine does not throw or throws and misses, it may not be viewed as all that abnormal.
Going back to Example 3.2.6, it is still the case that Suzy’s throw by itself is not a cause of the bottle shattering if ⟦BH = 0 ∧ ST = 0 ∧ BS = 0⟧ is not at least as normal as ⟦ST = 1 ∧ BS = 1⟧ according to the modified HP definition (extended to take normality into account). Similarly, Suzy’s throw is not a cause according to the original and updated HP definition if ⟦BT = 0 ∧ ST = 0 ∧ BS = 0⟧ is not at least as normal as ⟦ST = 1 ∧ BS = 1⟧. Since Billy not throwing is only one reason that Billy might not hit, ⟦BH = 0 ∧ ST = 0 ∧ BS = 0⟧ is at least as normal as ⟦BT = 0 ∧ ST = 0 ∧ BS = 0⟧. Thus, using the witness BT = 0 ∧ ST = 0 will not make Suzy’s throw a cause using the original and updated HP definition if it is not also a cause using the modified HP definition. Since we can always take BH = 0 to be the witness for the original and updated HP definition, all the variants of the HP definition will agree on whether ST = 1 is a cause of BS = 1.
Is it so unreasonable to declare both Billy and Suzy throwing a cause of the bottle shattering if ⟦BH = 0 ∧ ST = 0 ∧ BS = 0⟧ is not at least as normal as ⟦ST = 1 ∧ BS = 1⟧? Roughly speaking, this says that a situation where the bottle doesn’t shatter is extremely abnormal. Suzy’s throw is not the cause of the bottle shattering; it was going to happen anyway. The only way to get it not to happen is to intervene on both Suzy’s throw and Billy’s throw.
We can also apply these ideas to graded causality. Instead of comparing witness worlds, I now compare witness events. But rather than just considering the best witnesses, I can now consider all witnesses. That is, suppose that ![[image]](images/ddcleq0934.jpg) are the witnesses to
are the witnesses to ![[image]](images/ddcleq0935.jpg) being a cause of φ in
being a cause of φ in ![[image]](images/ddcleq0936.jpg) , and
, and ![[image]](images/ddcleq0937.jpg) are the witnesses to
are the witnesses to ![[image]](images/ddcleq0938.jpg) being a cause of φ in
being a cause of φ in ![[image]](images/ddcleq0939.jpg) . Now we can say that
. Now we can say that ![[image]](images/ddcleq0940.jpg) is at least as good a cause of φ in
is at least as good a cause of φ in ![[image]](images/ddcleq0941.jpg) as
as ![[image]](images/ddcleq0942.jpg) if
if
![[image]](images/ddcleq0943.jpg) (3.1)
(3.1)
That is, ![[image]](images/ddcleq0944.jpg) is at least as good a cause of φ in
is at least as good a cause of φ in ![[image]](images/ddcleq0945.jpg) as
as ![[image]](images/ddcleq0946.jpg) if the disjunction of the (formulas describing the) witness worlds for
if the disjunction of the (formulas describing the) witness worlds for ![[image]](images/ddcleq0947.jpg) being a cause of φ in
being a cause of φ in ![[image]](images/ddcleq0948.jpg) is at least as normal as the disjunction of the witness worlds for
is at least as normal as the disjunction of the witness worlds for ![[image]](images/ddcleq0949.jpg) being a cause of φ in
being a cause of φ in ![[image]](images/ddcleq0950.jpg) .
.
We can further extend this idea to parts of causes. (Recall that I earlier made the claim that it is arguably better to redefine cause to be what I am now calling part of a cause.) Suppose that ![[image]](images/dclimg0002.jpg) are all the causes of φ in
are all the causes of φ in ![[image]](images/dclimg0002.jpg) that include X = x as a conjunct, with
that include X = x as a conjunct, with ![[image]](images/dclimg0004.jpg) the corresponding witnesses. (It may be the case that
the corresponding witnesses. (It may be the case that ![[image]](images/dclimg0005.jpg) and
and ![[image]](images/dclimg0006.jpg) although the corresponding witnesses are different; a single cause may have a number of distinct witnesses.) Similarly, suppose that
although the corresponding witnesses are different; a single cause may have a number of distinct witnesses.) Similarly, suppose that ![[image]](images/dclimg0007.jpg) are all the causes of φ in
are all the causes of φ in ![[image]](images/dclimg0008.jpg) that include Y = y as a conjunct, with
that include Y = y as a conjunct, with ![[image]](images/dclimg0009.jpg) the corresponding witnesses. Again, we can say that X = x is at least as good a part of a cause for φ in
the corresponding witnesses. Again, we can say that X = x is at least as good a part of a cause for φ in ![[image]](images/dclimg0010.jpg) as Y = y if (3.1) holds.
as Y = y if (3.1) holds.
The analysis for all the examples in Section 3.4 remains unchanged using the alternative approach, with the exception of the causal chain example in Section 3.4.4. Now the analysis for the original and updated HP definition becomes the same as for the modified HP definition. To determine the best cause, we need to compare the normality of ⟦M = 1 ∧ ES = 0⟧ to that of ⟦LL = 1 ∧ ES = 0⟧. There is no reason to prefer one to the other; the length of the causal chain from M to ES plays no role in this consideration. As I said, this example can be dealt with by considering blame, without appealing to normality (see Section 6.2).
This modified definition of graded causality, using (3.1), has some advantages.
Example 3.5.1 There is a team consisting of Alice, Bob, Chuck, and Dan. In order to compete in the International Salsa Tournament, a team must have at least one male and one female member. All four of the team members are supposed to show up for the competition, but in fact none of them does. According to the original and updated definition, each of Alice, Bob, Chuck, and Dan is a cause of the team not being able to compete. However, using the alternative approach to graded causality, with (3.1), Alice is a better cause than Bob, Chuck, or Dan. Every context where Alice shows up and at least one of Bob, Chuck, or Dan shows up gives a witness world for Alice not showing up being a cause; the only witness worlds for Bob not showing up being a cause are those where both Alice and Bob show up. Thus, the set of witnesses for Alice being a cause is a strict superset of those for Bob being a cause. Under minimal assumptions on the normality ordering (e.g., the contexts where just Alice and Bob show up, the contexts where just Alice and Chuck show up, and the contexts where Alice and Dan show up are all mutually incomparable) a cause are incomparable both to the contexts where Chuck is a cause and the contexts where Dan is a cause, and similarly for Chuck and Dan), Alice is a better cause.
According to the modified HP definition, Alice by herself is not a cause for the team not being able to compete; neither is Bob. However, both are parts of a cause. The same argument then shows that Alice is a better part of a cause than Bob according to the modified HP definition.
With the normality definition in Section 3.2, each of Alice, Bob, Charlie, and Dan would be considered equally good causes according to the original and updated HP definition, and equally good parts of causes according to the modified HP definition. People do judge Alice to be a better cause; the alternative approach seems to capture this intuition better. (See also the discussion of Example 6.3.2 in Chapter 6.) ■
Although this alternative approach to AC2+(a) and graded causality deals with the rock-throwing example and gives reasonable answer in Example 3.5.1, it does not solve all the problems involving normality and causality, as the following example shows.
Example 3.5.2 A and B each control a switch. There are wires going from an electricity source to these switches and then continuing on to C. A must first decide whether to flip his switch left or right, then B must decide (knowing A’s choice). The current flows, resulting in a bulb at C turning on, iff both switches are in the same position. B wants to wants to turn on the bulb, so flips her switch to the same position as A does, and the bulb turns on.
Intuition suggests that A’s action should not be viewed as a cause of the C bulb being on, whereas B’s should. But suppose that we consider a model with three binary variables, A, B, and C. A = 0 means that A flips his switch left and A = 1 means that A flips his switch right; similarly for B. C = 0 if the bulb at C does not turn on, and C = 1 if it does. In this model, whose causal network is given in Figure 3.3, A’s value is determined by the context, and we have the equations
![[image]](images/fig3-3.jpg)
Figure 3.3: Who caused the bulb to turn on?
Without taking normality considerations into account, in the context where A = 1, both A = 1 and B = 1 are causes of C = 1, according to all variants of the HP definition. B = 1 is in fact a but-for cause of C = 1; to show that A = 1 is a cause of C = 1 for all variants of the HP definition, we can simply hold B at its actual value 1 and set A = 0. Similarly, for all other contexts, both A and B are causes of the outcome. However, people tend to view B as the only cause in all contexts.
Turning on a light bulb is ethically neutral. Does the situation change at all if instead of a bulb turning on, the result of the current flowing is that a person gets a shock?
Before considering normality, it is worth noting that the causal network in Figure 3.3 is isomorphic to that given in Figure 2.8 for Billy’s medical condition. Moreover, we can make the stories isomorphic by modifying the story in Example 2.4.1 slightly. Suppose we say that Billy is fine on Wednesday morning if exactly one doctor treats him and sick otherwise (so now BMC becomes a binary variable, with value 0 if Billy is fine on Wednesday morning and 1 if he is sick). If both doctors treat Billy, then I suspect most people would say that Tuesday’s doctor is the cause of Billy being sick; but if neither does, I suspect that Monday’s doctor would also be viewed as having a significant causal impact. Moreover, in the normal situation where Monday’s doctor treats Billy and Tuesday’s does not, I suspect that Monday’s doctor would be viewed as more of a cause of Billy feeling fine on Wednesday than Tuesday’s doctor.
If the HP definition is going to account for the differences between the stories, somehow normality considerations should do it. They do help to some extent in the second story. In particular, normality considerations work just right in the case that both doctors treat Billy (if we take the most normal situation to be the one where Monday’s doctor treats him and Tuesday’s doesn’t). But if neither doctor treats Billy, the same normality considerations suggest that Monday’s doctor is a better cause than Tuesday’s doctor. Although this may not be so unreasonable, I suspect that people would still be inclined to ascribe a significant degree of causality to Tuesday’s doctor. I return to this point below.
Now suppose instead that (what we have taken to be) the normal thing happens: just Monday’s doctor treats Billy. As expected, Billy feels fine on Wednesday. Most people would say that Monday’s doctor is the cause of Billy feeling fine, not Tuesdays’s doctor. Unfortunately, AC2+(a) (or AC2+(am)) is violated no matter who we try to view as the cause. What about graded causality? The witness for Monday’s doctor being a cause is sMT=0,TT=0,u; the witness for Tuesday’s doctor being a cause is sTT=1,u. In the first witness, we get two violations to normality: Billy’s doctor doesn’t do what he is supposed to do, nor does Tuesday’s doctor. In the second witness, we get only one violation (Tuesday’s doctor treating Billy when he shouldn’t). However, a case can still be made that the world where neither doctor treats Billy (MT = 0, TT = 0) should be viewed as more normal than the world where both do (MT = 1, TT = 1). The former witness might arise if, for example, both doctors are too busy to treat Billy. If Billy’s condition is not that serious, then they might sensibly decide that he can wait. However, for the second witness to arise, Tuesday’s doctor must have treated Billy despite Billy’s medical chart showing that Monday’s doctor treated him. Tuesday’s doctor could have also easily talked to Billy to confirm this. Arguably, this makes the latter world more of a violation of normality than the former. (The alternative approach works the same way for this example.)
When it comes to determining the cause of the bulb turning on, the situation is more problematic. Taking u to be the context where A = 1, both sA=0,B=1,u and sB=0,u seem less normal than su, and there seems to be no reason to prefer one to the other, so graded causality does not help in determining a cause. Similarly, for the alternative approach, both ⟦A = 0 ∧ B = 1 ∧ C = 0⟧ and ⟦B = 0 ∧ C = 0⟧ are less normal than either ⟦A = 1 ∧ C = 1⟧ or ⟦B = 1 ∧ C = 1⟧. Again, there is no reason to prefer B = 1 as a cause. If instead we consider the version of the story where, instead of a light bulb turning on, the result is a person being shocked, we can view both ⟦A = 0 ∧ B = 1 ∧ C = 0⟧ and ⟦B = 0 ∧ C = 0⟧ as more normal than either ⟦A = 1 ∧ C = 1⟧ or ⟦B = 1 ∧ C = 1⟧, since shocking someone can be viewed as abnormal. Now if we take normality into account, both A = 1 and B = 1 become causes, but there is still no reason to prefer B = 1.
We can deal with both of these issues by making one further change to how we take normality into account. Rather than considering the “absolute” normality of a witness, we can consider the change in normality in going from the actual world to the witness and prefer the witness that leads to the greatest increase (or smallest decrease) in normality. If the normality ordering is total, then whether we consider the absolute normality or the change in normality makes no difference. If witness w1 is more normal than witness w2, then the increase in normality from the actual world to w1 is bound to be greater than the increase in normality from the actual world to w2. But if the normality ordering is partial, then considering the change in normality from the actual world can make a difference.
Going back to Billy’s doctors, it seems reasonable to take the increase in normality going from sMT=1,TT=1,u to sMT=1,TT=0,u to be much greater than that of going from sMT=1,TT=1,u to sMT=0,TT=1,u. Thus, if both doctors treat Billy, then Tuesday’s doctor is a much better cause of Billy feeling sick on Wednesday than Monday’s doctor. In contrast, the increase in normality in going from sMT=0,TT=0,u to sMT=1,TT=0,u is arguably greater (although not much greater) than that of going from sMT=0,TT=0,u to sMT=0,TT=1,u. Thus, if neither doctor treats Billy, then Monday’s doctor is a better cause of Billy feeling sick on Wednesday than Tuesday’s doctor, but perhaps not a much better cause. Note that we can have such a relative ordering if the normality ordering is partial (in particular, if the worlds sMT=0,TT=0,u and sMT=1,TT=1,u are incomparable), but not if the normality ordering is total.
Similar considerations apply to the light bulb example. Now we can take the change from the world where both A = 1 and B = 1 to the world where A = 1 and B = 0 to be smaller than the one to the world where A = 0 and B = 1, because the latter change involves changing what A does as well as violating normality (in the sense that B does not act according to the equations), while the former change requires only that B violate normality. This gives us a reason to prefer B = 1 as a cause. ■
Considering not just how normal a witness is but the change in normality in going from the actual world to the witness requires a richer model of normality, where we can consider differences. I do not attempt to formalize such a model here, although I believe that it is worth exploring. These considerations also arise when dealing with responsibility (see Example 6.3.4 for further discussion).
Much of the material in this chapter is taken from [Halpern and Hitchcock 2015] (in some cases, verbatim); more discussion can be found there regarding the use of normality and how it relates to other approaches. A formal model that takes normality into account in the spirit of the definitions presented here already appears in preliminary form in the original HP papers [Halpern and Pearl 2001; Halpern and Pearl 2005a] and in [Halpern 2008]. Others have suggested incorporating considerations of normality and defaults in a formal definition of actual causality, including Hall [2007], Hitchcock [2007], and Menzies [2004, 2007].
The idea that normality considerations are important when considering causality goes back to the work of psychologists. Exploring the effect of norms on judgments of causality is also an active area of research. I mention here some representatives of this work, although these references do not do anywhere close to full justice to the ongoing work:
Approaches to giving semantics to typicality statements include preferential structures [Kraus, Lehmann, and Magidor 1990; Shoham 1987], ϵ-semantics [Adams 1975; Geffner 1992; Pearl 1989], possibility measures [Dubois and Prade 1991], and ranking functions [Goldszmidt and Pearl 1992; Spohn 1988]. The details of these approaches do not matter for our purposes; see [Halpern 2003] for an overview of these approaches. The approach used in Section 3.2 is the one used in [Halpern and Hitchcock 2015]; it can be viewed as an instance of preferential structures, which allow a partial preorder on worlds. By way of contrast, possibility measures and ranking functions put a total preorder on worlds. The model of causality that took normality considerations into account that I gave in [Halpern 2008] used ranking functions and, as a consequence, made the normality ordering total. Using a total normality order causes problems in some examples (see below).
There has been a great deal of discussion in the philosophy community regarding whether omissions count as causes. Beebee [2004] and Moore [2009], for example, argue against the existence of causation by omission in general; Lewis [2000, 2004] and Schaffer [2000a, 2004, 2012] argue that omissions are genuine causes in such cases; Dowe [2000] and Hall [2004] argue that omissions have a kind of secondary causal status; and McGrath [2005] argues that the causal status of omissions depends on their normative status. For example, Billy’s doctor’s failure to treat Billy is a cause of Billy’s sickness because he was supposed to treat Billy; the fact that other doctors also failed to treat Billy does not make them causes. As I observed in the main text, by taking an appropriate normality ordering, we can capture all these points of view. Wolff, Barbey, and Hausknecht [2010] and Livengood and Machery [2007] provide some experimental evidence showing how people view causality by omission and when they allow for causes that are omissions. Their results support the role of normality in these causality judgments (although the papers do not mention normality).
As I said in the main text, there have been claims that it is a mistake to focus on one cause. For example, John Stuart Mill [1856, pp. 360–361] writes:
…it is very common to single out one only of the antecedents under the denomination of Cause, calling the others mere Conditions. … The real cause, is the whole of these antecedents; and we have, philosophically speaking, no right to give the name of cause to one of them, exclusively of the others.
Lewis [1973a, pp. 558–559] also seems to object to this practice, saying:
We sometimes single out one among all the causes of some event and call it “the” cause, as if there were no others. Or we single out a few as the “causes”, calling the rest mere “causal factors” or “causal conditions”. … I have nothing to say about these principles of invidious discrimination.
Hall [2004, p. 228] adds:
When delineating the causes of some given event, we typically make what are, from the present perspective, invidious distinctions, ignoring perfectly good causes because they are not sufficiently salient. We say that the lightning bolt caused the forest fire, failing to mention the contribution of the oxygen in the air, or the presence of a sufficient quantity of flammable material. But in the egalitarian sense of “cause”, a complete inventory of the fire’s causes must include the presence of oxygen and of dry wood.
Sytsma, Livengood, and Rose [2012] conducted the follow-up to the Knobe and Fraser [2008] experiment discussed in Example 3.4.1 and Section 3.1. They had their subjects rate their agreement on a 7-point scale from 1 (completely disagree) to 7 (completely agree) with the statements “Professor Smith caused the problem” and “The administrative assistant caused the problem”. When they repeated Knobe and Fraser’s original experiment, they got an average rating of 4.05 for Professor Smith and 2.51 for the administrative assistant. Although their difference is less dramatic than Knobe and Fraser’s, it is still statistically significant. When they altered the vignette so that Professor Smith’s action was permissible, subjects gave an average rating of 3.0 for Professor Smith and 3.53 for the administrative assistant.
The bogus prevention problem is due to Hitchcock [2007]; it is based on an example due to Hiddleston [2005]. Using a normality ordering that is total (as I did in [Halpern 2008]) causes problems in dealing with Example 3.4.1. With a total preorder, we cannot declare (A = 1, B = 0, VS = 0) and (A = 0, B = 1, VS = 1) to be incomparable; we must compare them. To argue A = 1 is not a cause, we have to assume that (A = 1, B = 1, VS = 1) is more normal than (A = 0, B = 0, VS = 0). This ordering does not seem so natural.
Example 3.4.2 is due to Hitchcock [2007], where it is called “counterexample to Hitchcock”. Its structure is similar to Hall’s short-circuit example [Hall 2007, Section 5.3]; the same analysis applies to both. The observation that normality considerations deal well with it is taken from [Halpern 2015a]. The observation that normality considerations do not completely solve the railroad switch problem, as shown in Example 3.4.3, is due to Schumacher [2014]. The version of the switch problem with the variables LT and RT is essentially how Hall [2007] and Halpern and Pearl [2005a] modeled the problem. The voting examples in Section 3.4.3 are due to Livengood [2013]; the analysis given here in terms of normality is taken from [Halpern 2014a]. The analysis of all the other examples in Section 3.4 is taken from [Halpern and Hitchcock 2015].
For the details of Regina v. Faulkner, see [Regina v. Faulkner 1877]. Moore [2009] uses this type of case to argue that our ordinary notion of actual causation is graded, rather than all-or-nothing, and that it can attenuate over the course of a causal chain. In the postscript of [Lewis 1986b], Lewis uses the phrase “sensitive causation” to describe cases of causation that depend on a complex configuration of background circumstances. For example, he describes a case where he writes a strong letter of recommendation for candidate A, thus earning him a job and displacing second-place candidate B, who then accepts a job at her second choice of institution, displacing runner-up C, who then accepts a job at another university, where he meets his spouse, and they have a child, who later dies. Lewis claims that although his writing the letter is indeed a cause of the death, it is a highly sensitive cause, requiring an elaborate set of detailed conditions to be present. Woodward [2006] says that such causes are “unstable”. Had the circumstances been slightly different, writing the letter would not have produced this effect (either the effect would not have occurred or it would not have been counterfactually dependent on the letter). Woodward argues that considerations of stability often inform our causal judgments. The extended HP definition allows us to take these considerations into account.
The Watson v. Kentucky and Indiana Bridge and Railroad can be found in [Watson v. Kentucky and Indiana Bridge and Railroad 1910].
Sander Beckers [private communication, 2015] pointed out that putting a normality ordering on worlds does not really solve the problem of making BT = 1 part of a cause of BS = 1 (see the discussion after Example 3.2.6), thus providing the impetus for the alternative definition of normality discussed in Section 3.5. Example 3.5.1 is due to Zultan, Gerstenberg, and Lagnado [2012], as are the experiments showing that people view Alice as a better cause than Bob in this example. The work of Zultan, Gerstenberg, and Lagnado related to this example is discussed further in the notes to Chapter 6. The example of C being shocked in Example 3.5.2 is due to McDermott [1995]. He viewed it as an example of lack of transitivity: A’s flipping right causes B to flip right, which in turn causes C to get a shock, but most people don’t view A’s flip as being a cause of C’s shock, according to McDermott. As I observed, normality considerations can also be used to give us this outcome. Various approaches to extending a partial ordering ⪰ on worlds to an ordering ⪰e on events are discussed in [Halpern 1997]; the notation ⪰ is taken from [Halpern 2003].
The Art of Causal Modeling
Fashion models and financial models are similar. They bear a similar relationship to the everyday world. Like supermodels, financial models are idealized representations of the real world, they are not real, they don’t quite work the way that the real world works. There is celebrity in both worlds. In the end, there is the same inevitable disappointment.
Satyajit Das, Traders, Guns & Money: Knowns and Unknowns in the Dazzling World of Derivatives
Essentially, all models are wrong, but some are useful.
G. E. P. Box and N. R. Draper, Empirical Model Building and Response Surfaces
In the HP definition of causality, causality is relative to a causal model. X = x can be the cause of φ in one causal model and not in another. Many features of a causal model can impact claims of causality. It is clear that the structural equations can have a major impact on the conclusions we draw about causality. For example, it is the equations that allow us to conclude that lower air pressure is the cause of the lower barometer reading and not the other way around; increasing the barometer reading will not result in higher air pressure.
But it is not just the structural equations that matter. As shown by the Suzy-Billy rock-throwing example (Example 2.3.3), adding extra variables to a model can change a cause to a non-cause. Since only endogenous variables can be causes, the split of variables into exogenous and endogenous can clearly affect what counts as a cause, as we saw in the case of the oxygen and the forest fire. As a number of examples in Chapter 3 showed, if we take normality considerations into account, the choice of normality ordering can affect causality. Even the set of possible values of the variables in the model makes a difference, as Example 2.3.7 (where both the sergeant and captain give orders) illustrates.
Some have argued that causality should be an objective feature of the world. Particularly in the philosophy literature, the (often implicit) assumption has been that the job of the philosopher is to analyze the (objective) notion of causation, rather like that of a chemist analyzing the structure of a molecule. In the context of the HP approach, this would amount to designating one causal model as the “right” model. I do not believe that there is one “right” model. Indeed, in the spirit of the quote at the beginning of this chapter, I am not sure that there are any “right” models, but some models may be more useful, or better representations of reality, than others. Moreover, even for a single situation, there may be several useful models. For example, suppose that we ask for the cause of a serious traffic accident. A traffic engineer might say that the bad road design was the cause; an educator might focus on poor driver education; a sociologist might point to the pub near the highway where the driver got drunk; a psychologist might say that the cause is the driver’s recent breakup with his girlfriend. Each of these answers is reasonable. By appropriately choosing the variables, the structural-equations framework can accommodate them all.
That said, it is useful to have principles by which we can argue that one model is more reasonable/useful/appropriate than another. Suppose that a lawyer argues that, although his client was drunk and it was pouring rain, the cause of the accident was the car’s faulty brakes, which is why his client is suing GM for $5,000,000. If the lawyer were using the HP definition of causality, he would then have to present a causal model in which the brakes were the cause. His opponent would presumably then present a different model in which the drunkenness or the rain was a cause. We would clearly want to say that a model that made the faulty brakes a cause because it did not include the rain as an endogenous variable, or it took drunkenness to be normal, was not an appropriate model.
The structural equations can be viewed as describing objective features of the world. At least in principle, we can test the effects of interventions to see whether they are correctly captured by the equations. In some cases, we might be able to argue that the set of values of variables is somewhat objective. In the example above, if C can only report values 0 and 1, then it seems inappropriate to take {0, 1, 2} to be its set of values. But clearly what is exogenous and what is endogenous is to some extent subjective, as is the choice of variables, and the normality ordering. Is there anything useful that we can say about them? In this chapter, I look at the issue and its impact more carefully.
4.1 Adding Variables to Structure a Causal Scenario
A modeler has considerable leeway in choosing which variables to include in a model. As the Suzy-Billy rock-throwing example shows, if we want to argue that X = x is the cause of φ rather than Y = y, then there must be a variable that takes on different values depending on whether X = x or Y = y is the actual cause. If the model does not contain such a variable, then there is no way to argue that X = x is the cause. There is a general principle at play here. Informally, say that a model is insufficiently expressive if it cannot distinguish two different scenarios (intuitively, ones for which we would like to make different causal attributions). The naive rock-throwing model of Figure 2.2, which just has the endogenous variables ST, BT, and BS, is insufficiently expressive in this sense because it cannot distinguish between a situation where Suzy and Billy’s rock hit the bottle simultaneously (in which case we would want to call Billy’s throw a cause) and the one where Suzy hits first (so Billy’s throw is not a cause). What about the bogus prevention example from Section 3.4.2? As we saw, here too adding an extra variable can give us a more reasonable outcome (without appealing to normality considerations). I would argue that in this case as well, the problem is that the original model was insufficiently expressive.
The next four examples show the importance of having variables that bring out the causal structure of a scenario and to distinguish two causal scenarios. One way of understanding the role of the variables SH and BH in the rock-throwing example is that they help us distinguish the scenario where Suzy and Billy hit simultaneously from the one where Suzy hits first. The following examples show that this need to distinguish scenarios is quite widespread.
Example 4.1.1 There are four endogenous binary variables, A, B, C, and S, taking values 1 (on) and 0 (off). Intuitively, A and B are supposed to be alternative causes of C, and S acts as a switch. If S = 0, the causal route from A to C is active and that from B to C is dead; and if S = 1, the causal route from A to C is dead and the one from B to C is active. There are no causal relations between A, B, and S; their values are determined by the context. The equation for C is C = (¬S ∧ A) ∨ (S ∧ B).
Suppose that the context is such that A = B = S = 1, so C = 1. B = 1 is a but-for cause of C = 1, so all the variants of the HP definition agree that it is a causes, as we would hope. Unfortunately, the original and updated definition also yield A = 1 as a cause of C = 1. The argument is that in the contingency where S is set to 0, if A = 0, then C = 0, whereas if A = 1, then C = 1. This does not seem so reasonable. Intuitively, if S = 1, then the value of A is irrelevant to the outcome. Considerations of normality do not help here; all worlds seem to be equally normal. Although the modified HP definition does not take A = 1 to be a cause, it is part of a cause: A = 1 S = 1 is a cause of C = 1 because if A and S are both set to 0, C = 0.
This might seem to represent a victory for the modified HP definition, but the situation is a little more nuanced. Consider a slightly different story. This time, we view B as the switch, rather than S. If B = 1, then C = 1 if either A = 1 or S = 1; if B = 0, then C = 1 only if A = 1 and S = 0. That is, C = (B ∧ (A ∨ S)) ∨ (¬B ∧ A ∧ ¬S). Although this is perhaps not as natural a story as the original, such a switch is surely implementable. In any case, a little playing with propositional logic shows that, in this story, C satisfies exactly the same equation as before: (¬S ∧ A) ∨ (S ∧ B) is equivalent to (B ∧ (A ∨ S)) ∨ (¬B ∧ A ∧ ¬S). The key point is that, unlike the first story, in the second story, it seems to me quite reasonable to say that A = 1 is a cause of C = 1 (as is B = 1). Having A = 1 is necessary for the first “mechanism” to work. But as long as we model both stories using just the variables A, B, C, and S, they have the same models with the same equations, so no variant of the HP definition can distinguish them.
Given that we have different causal intuitions for the stories, we should model them differently. One way to distinguish them is to add two more endogenous random variables, say D and E, that describe the ways that C could be 1. In the original story, we would have the equations D = ¬S ∧ A, E = S ∧ B, and C = D ∨ E. In this model, since D = 0 in the actual context, it is not hard to see that all variants of the HP definition agree that A = 1 is not a cause of C = 1 (nor is it part of a cause), whereas B = 1 and S = 1 are causes, as they should be. Thus, in this model, we correctly capture our intuitions for the original story.
To capture the second story, we can add variables D′ and E′ such that D′ = B ∧ (A ∨ S), E′ = ¬B ∧ A ∧ S, and C = D′ ∨ E′. In this model, it is not hard to see that according to the original and updated definition, all of A = 1, B = 1, and S = 1 are causes of C = 1; according to the modified HP definition, the causes stay the same: B = 1 and A = 1 ∧ S = 1.
Now, as I said above, we can certainly create these setups in the real world. Consider the original story. We can design a circuit where there is a source of power at A and B, a physical switch at S, and a bulb at C that turns on (C = 1) if either the circuit is connected to A (A = 1) and the switch is turned left (S = 0) or the circuit is connected to B (B = 1) and the switch is turned right (S = 1). We can similarly design a circuit that captures the second story. With this circuit, we can think of D as representing “there is current flowing between power source A and bulb C”; there are similar physical analogues of E, D′, and E′. But even without physical analogues, these “structuring” variables can play an important role. Suppose that the agent does not see the underlying physical setup. All he sees are switches corresponding to A, B, and S, which can be manipulated. In the first setup, flipping the switch for A connects or disconnects the circuit and the A battery, and similarly for B, while flipping the switch for S connects C either to the A or B battery. In the second story, the switches for A, B, and S work differently, but as far as the observer is concerned, all interventions lead to the same outcome on the bulb C in both cases. A modeler could usefully introduce D and E (resp., D′ and E′) to disambiguate these models. These variables can be viewed as the modeler’s proxies for the underlying physical circuit; they help describe the mechanisms that result in C being 1.
Note that we do not want to think of D as being defined to take the value 1 if A = 1 and S = 0. For then we could not intervene to set D = 0 if A = 1 and S = 0. Adding a variable to the model commits us to being able to intervene on it. (I return to this point in Section 4.6.) In the real world, setting D to 0 despite having A = 1 and S = 0 might correspond to the connection being faulty when the switch is turned left. ■
Example 4.1.2 A lamp L is controlled by three switches, A, B, and C, each of which has three possible positions, −1, 0, and 1. The lamp switches on iff two or more of the switches are in the same position. Thus, L = 1 iff (A = B) ∨ (B = C) ∨ (A = C). Suppose that, in the actual context, A = 1, B = −1, and C = −1. Intuition suggests that although B = −1 and C = −1 should be causes of L = 1, A = 1 should not: since the setting of A does not match that of either B or C, it has no causal impact on the outcome.
Since B = −1 and C = −1 are but-for causes of L = 1, all three variants of the HP definition declare them to be causes. Unfortunately, the original and updated definition also declare A = 1 to be a cause. For in the contingency where B = 1 and C = −1, if A = 1, then L = 1, whereas if A = 0, then L = 0. Adding defaults to the picture does not solve the problem. Again, the modified HP definition does the “right” thing here and does not declare A = 1 to be a cause or even part of a cause.
However, just as in Example 4.1.1, another story can be told here, where the observed variables have the same values and are connected by the same structural equations. Now suppose that L = 1 iff either (a) none of A, B, or C is in position −1; (b) none of A, B, or C is in position 0; or (c) none of A, B, or C is in position 1. It is easy to see that the equations for L are literally the same as in the original example. But now it seems more reasonable to say that A = 1 is a cause of L = 1. Certainly A = 1 causes L = 1 as a result of no values being 0; had A been 0, then the lamp would still have been on, but now it would be as a result of no values being −1. Considering the contingency where B = 1 and C = −1 “uncovers” the causal impact of A.
Again, the distinction between the two stories can be captured by adding more variables. For the second story, add the variables NOT (−1), NOT (0), and NOT (1), where NOT (i) is 1 iff none of A, B, or C is i. Then L = NOT (−1) ∨ NOT (0) ∨ NOT (1). Now all three variants of the HP definition agree that A = 1 is a cause of L = 1 (as well as B = −1 and C = 1). For the original story, add the variables TWO (−1), TWO (0), and TWO (1), where TWO (i) = 1 iff at least two of A, B, and C are i, and take L = TWO (−1) ∨ TWO (0) ∨ TWO(1). In this case, all three variants agree that A = 1 is not a cause of L = 1 (whereas B = −1 and C = −1 continue to be causes).
Once again, I think of the variables NOT (−1), NOT (0), and NOT (1) (resp., TWO (−1), TWO (0), and TWO (1)) as “structuring” variables that help the modeler distinguish the two scenarios and, specifically, the mechanisms that lead to the lamp turning on.
This example (and the others in this section) show that causality is to some extent dependent on how we describe a situation. If we describe the rule for the lamp being on as “it is on if two or more of the switches are in the same position”, we get a different answer than if we say “it is on if there is a position such that none of the switches are in that position”, despite the fact that these two rules lead to the same outcomes. This seems to me compatible with human ascriptions of causality. But even if accept that, where does this leave a modeler who is thinking in terms of, say, the first rule, and to whom the second rule does not even occur? My sense is that the description of the first rule naturally suggests a “structuring” in terms of the variables TWO (−1), TWO (0), and TWO (1), so it is good modeling practice to add these variables even if no other way of structuring the story occurs to the modeler. ■
Example 4.1.3 Consider a model M with four endogenous variables, A, B, D, and E. The values of A and D are determined by the context. The values of B and E are given by the equations B = A and E = D. Suppose that the context u is such that A = D = 1. Then clearly, in (M, u), A = 1 is a cause of B = 1 and not a cause of E = 1, whereas D = 1 is a cause of E = 1 and not of B = 1. The problem comes if we replace A in the model by X, where, intuitively, X = 1 iff A and D agree (i.e., X = 1 if the context would have been such that A = D = 1 or A = D = 0). The value of A can be recovered from the values of D and X. Indeed, it is easy to see that A = 1 iff X = D = 1 or X = D = 0. Thus, we can rewrite the equation for B by taking B = 1 iff X = D = 1 or X = D = 0. Formally, we have a new model M ′ with endogenous variables X, B, D, and E. The value of D and X is given by the context; as suggested above, equations for the B and E are
![[image]](images/eqn1.jpg)
![[image]](images/eqn2.jpg)
The context u is such that D = X = 1, so B = E = 1. In (M′, u), it is still the case that D = 1 is a cause of E = 1, but now D = 1 is also a cause of B = 1.
Is it so unreasonable that D = 1 is a cause of B = 1 in M′ but is not a cause of B = 1 in M? Of course, if we have in mind the story represented by model M, then it is unreasonable for D = 1 to be a cause. But M′ can also represent quite a different situation. Consider the following two stories. We are trying to determine the preferences of two people, Betty and Edward, in an election. B = 1 if Betty is recorded as preferring the Democrats and B = 0 if Betty is recorded as preferring the Republicans, and similarly for E. In the first story, we send Alice to talk to Betty and David to talk to Edward to find out their preferences (both are assumed to be truthful and good at finding things out). When Alice reports that Betty prefers the Democrats (A = 1), then Betty is reported as preferring the Democrats (B = 1); similarly for David and Edward. Clearly, in this story (which is modeled by M), D = 1 causes E = 1 but not B = 1.
But now suppose instead of sending Alice to talk to Betty, Xavier is sent to talk to Carol, who knows only whether Betty and Edward have the same preferences. Carol tells Xavier that they indeed have the same preferences (X = 1). Upon hearing that X = D = 1, the vote tabulator correctly concludes that B = 1. This story is modeled by M′. But in this case, it strikes me as perfectly reasonable that D = 1 should be a cause of B = 1. This is true despite the fact that if we had included the variable A in M′, it would have been the case that A = B = 1.
Again, we have two different stories; we need to have different models to disambiguate them. ■
At the risk of overkill, here is yet one more example:
Example 4.1.4 A ranch has five individuals: a1,…, a5. They have to vote on two possible outcomes: staying at the campfire (O = 0) or going on a round-up (O = 1). Let Ai be the random variable denoting ai’s vote, so Ai = j if ai votes for outcome j. There is a complicated rule for deciding on the outcome. If a1 and a2 agree (i.e., if A1 = A2), then that is the outcome. If a2,…, a5 agree and a1 votes differently, then the outcome is given by a1’s vote (i.e., O = A1). Otherwise, majority rules. In the actual situation, A1 = A2 = 1 and A3 = A4 = A5 = 0, so by the first mechanism, O = 1. The question is what were the causes of O = 1.
Using the naive causal model with just the variables A1,…, A5, O, and the obvious equations describing O in terms of A1,…, A5, it is almost immediate that A1 = 1 is a but-for cause of O = 1. Changing A1 to 0 results in O = 0. Somewhat surprisingly, in this naive model, A2 = 1, A3 = 0, A4 = 0, and A5 = 0 are also causes according to the original and updated HP definition. To see that A2 = 1 is a cause, consider the contingency where A3 = 1. Now if A2 = 0, then O = 0 (majority rules); if A2 = 1, then O = 1, since A1 = A2 = 1, and O = 1 even if A3 is set back to its original value of 0. The argument that A3 = 0, A4 = 0, and A5 = 0 are causes according to the original and updated definition is the same; I will give the argument for A3 = 0 here. Consider the contingency where A2 = 0, so that all voters but a1 vote for 0 (staying at the campsite). If A3 = 1, then O = 0 (majority rules). If A3 = 0, then O = 1, by the second mechanism (a1 is the only vote for 0), whereas if A2 is set to its original value of 1, then we still have O = 1, now by the first mechanism. Although the modified HP definition does not declare any of A2 = 1, A3 = 0, A4 = 0, or A5 = 0 to be causes, it does declare each of the conjunctions A2 = 1 ∧ A3 = 0, A2 = 1 ∧ A4 = 0, and A2 = 1 ∧ A5 = 0 to be a cause; for example, if the values of A2 and A3 are changed, then O = 0. So, according to the modified HP definition, each of A2 = 1, A3 = 0, A4 = 0, and A5 = 0 is part of a cause.
An arguably better model of the story is suggested by the analysis, which talks about the first and second mechanisms. This, in turn, suggests that the choice of mechanism should be part of the model. There are several ways of doing this. One is to add three new variables, call them M1, M2, and M3. These variables have values in {0, 1, 2}, where Mj = 0 if mechanism j is active and suggests an outcome 0, Mj = 1 if mechanism j is active and suggests an outcome of 1, and Mj = 2 if mechanism j is not active. (We actually don’t need the value M3 = 2; mechanism 3 is always active, because there is always a majority with 5 voters, all of whom must vote.) There are obvious equations linking the value of M1, M2, and M3 to the values of A1,…, A5. (Actually, since the mechanisms are now represented by variables that can be intervened on, we would have to define what happens as a result of an “unnatural” intervention that sets both M1 = 1 and M2 = 1; for definiteness, say in that case that mechanism M1 is applied.)
Now the value of O just depends on the values of M1, M2, and M3: if M1 ≠ 2, then O = M1; if M1 = 2 and M2 ≠ 2, then O = M2; and if M1 = M2 = 2, then O = M3. It is easy to see that in this model, in the context where A1 = A2 = 1 and A3 = A4 = A5 = 0, then, according to all the variants of the HP definition, none of A3 = 0, A4 = 0, or A5 = 0 is a cause, whereas A1 = 1 is a cause, as we would expect, as are A2 = 1 and M2 = 1. This seems reasonable: the second mechanism was the one that resulted in the outcome, and it required A1 = A2 = 1.
Now suppose that we change the description of the voting rule. We take O = 1 if one of the following two mechanisms applies:
It is not hard to check that, although the description is different, O satisfies the same equation in both stories. But now it does not seem so unreasonable that A2 = 1, A3 = 0, A4 = 0, and A5 = 0 are causes of O = 1. And indeed, if we construct a model in terms of these two mechanisms (i.e., add variables ![[image]](images/dclimg0011.jpg) and
and ![[image]](images/dclimg0012.jpg) that correspond to these two mechanisms), then it is not hard to see that A1 = 1, A2 = 1, A3 = 0, A4 = 0, and A5 = 0 are all causes according to the original and updated HP definition. With the modified definition, things are unchanged: A1 = 1, A2 = 1 ∧ A3 = 0, A2 = 1 ∧ A4 = 0, and A2 = 1 ∧ A5 = 0 continue to be causes (again, {A2, A3}, {A2, A4}, and {A2, A5} are minimal sets of variables whose values have to change to change the outcome if the first mechanism is used).
that correspond to these two mechanisms), then it is not hard to see that A1 = 1, A2 = 1, A3 = 0, A4 = 0, and A5 = 0 are all causes according to the original and updated HP definition. With the modified definition, things are unchanged: A1 = 1, A2 = 1 ∧ A3 = 0, A2 = 1 ∧ A4 = 0, and A2 = 1 ∧ A5 = 0 continue to be causes (again, {A2, A3}, {A2, A4}, and {A2, A5} are minimal sets of variables whose values have to change to change the outcome if the first mechanism is used).
Here the role of the structuring variables M1, M2, and M3 (resp. ![[image]](images/dclimg0013.jpg) and
and ![[image]](images/dclimg0014.jpg) ) as descriptors of the mechanism being invoked seems particularly clear. For example, setting M1 = 2 says that the first mechanism will not be applied, even if A1 = A2; setting M1 = 1 says that we act as if both a1 and a2 voted in favor, even if that is not the case. ■
) as descriptors of the mechanism being invoked seems particularly clear. For example, setting M1 = 2 says that the first mechanism will not be applied, even if A1 = A2; setting M1 = 1 says that we act as if both a1 and a2 voted in favor, even if that is not the case. ■
The examples considered so far in this section show how, by adding variables that describe the mechanism of causality, we can distinguish two situations that otherwise seem identical. As the following example shows, adding variables that describe the mechanism also allows us to convert a part of a cause (according to the modified HP definition) to a cause.
Example 4.1.5 Suppose that we add variables A, B, and C to the disjunctive forest-fire example (Example 2.3.1), where A = L ∧ ¬MD, B = ¬L ∧ MD, and C = L ∧ MD. We then replace the earlier equation for FF (i.e., FF = L ∨ MD) by FF = A ∨ B ∨ C. The variables A, B, and C can be viewed as describing the mechanism by which the forest fire happened. Did it happen because of the dropped match only, because of the lightning only, or because of both? In this model, not only are L = 1 and MD = 1 causes of FF = 1 according to the original and updated HP definition, they are also causes according to the modified definition. For if we fix A and B at their actual values of 0, then FF = 0 if L is set to 0, so AC2(am) is satisfied and L = 1 is a cause; an analogous argument applies to MD.
I would argue that this is a feature of the modified definition, not a bug. Suppose, for example, that we interpret A, B, and C as describing the mechanism by which the fire occurred. If these variables are in the model, then this suggests that we care about the mechanism. The fact that L = 1 is part of the reason that FF = 1 occurred thanks to mechanism C. Although the forest fire would still have occurred if the lightning hadn’t struck, it would have been due to a different mechanism. (As an aside, adding mechanisms in this way is actually a general approach for converting conjunctive causes in the the modified HP definition to single conjuncts. It is easy to see that a similar approach would work for Example 2.3.2, where Suzy wins the election 11–0, although now we would have to add ![[image]](images/dclimg0015.jpg) new variables, one for each possible subset of 6 voters.)
new variables, one for each possible subset of 6 voters.)
In the original model, we essentially do not care about the details of how the fire comes about. Now suppose that we care only about whether lightning was a cause. In that case, we would add only the variable B, with B = ¬L ∧ MD, as above, and set FF = L ∨ B. In this case, in the context where L = MD = 1, all three variants of the HP definition agree that only L = 1 is a cause of FF = 1; MD = 1 is not (and is not even part of a cause). Again, I would argue that this is a feature. The structure of the model tells us that we should care about how the fire came about, but only to the extent of whether it was due to L = 1. In the actual context, MD = 1 has no impact on whether L = 1.
But now consider the variant of the disjunctive model considered in Example 2.9.1. Recall that in this variant, there are two arsonists; in the abnormal setting where only one of them drops a match, FF = 2: there is a less significant fire. In this model, MD = 1 is a cause of the forest fire according to modified HP definition, as we would expect, but L = 1 is not even part of a cause, since L = 1∧ MD = 1 is no longer a cause (MD = 1 is a cause all by itself). This seems at least mildly disconcerting. But now normality considerations save the day. By assumption, the witness MD = 1 ∧ MD′ = 0 ∧ FF = 2 needed to declare MD = 1 a cause is abnormal, so AC2+(am) does not hold. Using graded causality, L = 1 ∧ MD = 1 is a better cause than MD = 1. ■
In the rock-throwing example, by adding the variables SH and BH, and moving from the naive model MRT to ![[image]](images/dclimg0016.jpg) , BT = 1 changed from being a cause to not being a cause of BS = 1. Similarly, adding extra variables affected causality in all the examples in Section 4.1. Of course, without any constraints, it is easy to add variables to get any desired result. For example, consider the “sophisticated” rock-throwing model M′RT. Suppose that a variable BH1 is added with equations that set BH1 = BT and BS = SH ∨ BT ∨ BH1, giving a new causal model
, BT = 1 changed from being a cause to not being a cause of BS = 1. Similarly, adding extra variables affected causality in all the examples in Section 4.1. Of course, without any constraints, it is easy to add variables to get any desired result. For example, consider the “sophisticated” rock-throwing model M′RT. Suppose that a variable BH1 is added with equations that set BH1 = BT and BS = SH ∨ BT ∨ BH1, giving a new causal model ![[image]](images/dclimg0017.jpg) . In
. In ![[image]](images/dclimg0018.jpg) , there is a new causal path from BT to BS going through BH1, independent of all other paths. Not surprisingly, in
, there is a new causal path from BT to BS going through BH1, independent of all other paths. Not surprisingly, in ![[image]](images/dclimg0019.jpg) , BT = 1 is indeed a cause of BS = 1.
, BT = 1 is indeed a cause of BS = 1.
But this seems like cheating. Adding this new causal path fundamentally changes the scenario; Billy’s throw has a new way of affecting whether the bottle shatters. Although it seems reasonable to refine a model by adding new information, we want to do so in a way that does not affect what we know about the old variables. Intuitively, suppose that we had a better magnifying glass and could look more carefully at the model. We might discover new variables that were previously hidden. But we want it to be the case that any setting of the old variables results in the same observations. That is, while adding the new variable refines the model, it does not fundamentally change it. This is made precise in the following definition.
Definition 4.2.1 A causal model ![[image]](images/dclimg0020.jpg) is a conservative extension of
is a conservative extension of ![[image]](images/dclimg0021.jpg) if
if ![[image]](images/dclimg0022.jpg) ,
,![[image]](images/dclimg0023.jpg) and for all contexts
and for all contexts ![[image]](images/dclimg0024.jpg) , all variables X ∈ V, and all settings
, all variables X ∈ V, and all settings ![[image]](images/dclimg0025.jpg) of the variables in
of the variables in ![[image]](images/dclimg0026.jpg) , we have
, we have ![[image]](images/dclimg0027.jpg) iff
iff ![[image]](images/dclimg0028.jpg) . That is, no matter how we set the variables in M other than X, X has the same value in context
. That is, no matter how we set the variables in M other than X, X has the same value in context ![[image]](images/dclimg0029.jpg) in both M and M′. ■
in both M and M′. ■
According to Definition 4.2.1, M′ is a conservative extension of M iff, for certain formulas ψ involving only variables in ![[image]](images/dclimg0030.jpg) , namely, those of the form
, namely, those of the form ![[image]](images/dclimg0031.jpg) ,
, ![[image]](images/dclimg0032.jpg) iff
iff ![[image]](images/dclimg0033.jpg) . As the following lemma shows, this is actually true for all formulas involving only variables in
. As the following lemma shows, this is actually true for all formulas involving only variables in ![[image]](images/dclimg0034.jpg) , not just ones of a special form. (It is perhaps worth noting that here is a case where we cannot get away with omitting the causal model when using statisticians’ notation. The notion of a conservative extension requires comparing the truth of the same formula in two different causal models.)
, not just ones of a special form. (It is perhaps worth noting that here is a case where we cannot get away with omitting the causal model when using statisticians’ notation. The notion of a conservative extension requires comparing the truth of the same formula in two different causal models.)
Lemma 4.2.2 Suppose that M′ is a conservative extension of ![[image]](images/dclimg0035.jpg) . Then for all causal formulas φ that mention only variables in
. Then for all causal formulas φ that mention only variables in ![[image]](images/dclimg0036.jpg) and all contexts
and all contexts![[image]](images/dclimg0037.jpg) , we have
, we have ![[image]](images/dclimg0038.jpg) iff
iff ![[image]](images/dclimg0039.jpg) .
.
It is not hard to show that the “sophisticated” model for the rock-throwing example ![[image]](images/dclimg0040.jpg) is a conservative extension of MRT.
is a conservative extension of MRT.
Proposition 4.2.3 ![[image]](images/dclimg0041.jpg) is a conservative extension of MRT.
is a conservative extension of MRT.
Proof: It suffices to show that, whatever the setting of U, BT, and ST, the value of BS is the same in both MRT and ![[image]](images/dclimg0042.jpg) . It is easy to check this by considering all the cases: in both models, BS = 1 if either ST = 1 or BT = 1, and BS = 0 if ST = BT = 0 (independent of the value of U). ■
. It is easy to check this by considering all the cases: in both models, BS = 1 if either ST = 1 or BT = 1, and BS = 0 if ST = BT = 0 (independent of the value of U). ■
The model ![[image]](images/dclimg0043.jpg) , which has additional endogenous variables SA, BA, SF, and BF, is not a conservative extension of either
, which has additional endogenous variables SA, BA, SF, and BF, is not a conservative extension of either ![[image]](images/dclimg0044.jpg) or MRT. The fact that Suzy and Billy are accurate shots and that, if both throw, Suzy hits first, are no longer baked in with
or MRT. The fact that Suzy and Billy are accurate shots and that, if both throw, Suzy hits first, are no longer baked in with ![[image]](images/dclimg0045.jpg) . This means that
. This means that ![[image]](images/dclimg0046.jpg) differs from MRT and
differs from MRT and ![[image]](images/dclimg0047.jpg) in some fundamental ways. We can’t really think of the contexts as being the same in MRT and
in some fundamental ways. We can’t really think of the contexts as being the same in MRT and ![[image]](images/dclimg0048.jpg) ; the context in
; the context in ![[image]](images/dclimg0049.jpg) determines the values of BA, SA, BF, and SF, as well as that of ST and BT.
determines the values of BA, SA, BF, and SF, as well as that of ST and BT.
As this discussion shows, the requirement in Definition 4.2.1 that ![[image]](images/dclimg0050.jpg) is quite a strong one. Roughly speaking, it says that whatever extra endogenous variables are added in going from M to M′, their values are determined by the (exogenous and endogenous) variables already in M. This is the case in going from MRT to
is quite a strong one. Roughly speaking, it says that whatever extra endogenous variables are added in going from M to M′, their values are determined by the (exogenous and endogenous) variables already in M. This is the case in going from MRT to ![[image]](images/dclimg0051.jpg) : the value of SH is determined by that of ST, whereas the value of BH is determined by that of SH and BT. However, this is not the case in going from
: the value of SH is determined by that of ST, whereas the value of BH is determined by that of SH and BT. However, this is not the case in going from ![[image]](images/dclimg0052.jpg) to
to ![[image]](images/dclimg0053.jpg) . For example, nothing in
. For example, nothing in ![[image]](images/dclimg0054.jpg) determines the value of BA or SA; both are implicitly assumed to always be 1 in
determines the value of BA or SA; both are implicitly assumed to always be 1 in ![[image]](images/dclimg0055.jpg) . At the end of Section 4.4, I discuss a context-relative generalization of the notion of conservative extension that can be applied to
. At the end of Section 4.4, I discuss a context-relative generalization of the notion of conservative extension that can be applied to ![[image]](images/dclimg0056.jpg) and
and ![[image]](images/dclimg0057.jpg) . For now, I continue with the notion of conservative extension as defined above. It is quite widely applicable. In particular, in all the examples in Section 4.1, the model obtained by adding extra variables is a conservative extension of the original model. This can be proved by using arguments similar to those used in Proposition 4.2.3; I leave details to the reader.
. For now, I continue with the notion of conservative extension as defined above. It is quite widely applicable. In particular, in all the examples in Section 4.1, the model obtained by adding extra variables is a conservative extension of the original model. This can be proved by using arguments similar to those used in Proposition 4.2.3; I leave details to the reader.
4.3 Using the Original HP Definition Instead of the Updated Definition
Recall that Example 2.8.1 was the one that originally motivated using the updated rather than the orignal HP definition. In this example, a prisoner dies either if A loads B’s gun and B shoots, or if C loads and shoots his gun. In the actual context u, A loads B’s gun, B does not shoot, but C does load and shoot his gun, so that the prisoner dies. The original HP definition, using AC2(bo), would declare A = 1 a cause of D = 1 (the prisoner dies); the updated definition, using AC2(bu), would not, provided that only the variables A, B, C, and D are used. But, as I showed, by adding an additional variable, the original HP definition gives the desired result. The following result, proved in Section 4.8.2, shows that this approach generalizes: we can always use the original HP definition rather than the updated HP definition by adding extra variables.
Theorem 4.3.1 If X = x is not a cause of Y = y in ![[image]](images/dclimg0058.jpg) according to the updated HP definition but is a cause according to the original HP definition, then there is a model M′ that is a conservative extension of M such that X = x is not a cause of Y = y in
according to the updated HP definition but is a cause according to the original HP definition, then there is a model M′ that is a conservative extension of M such that X = x is not a cause of Y = y in ![[image]](images/dclimg0059.jpg) according to either the original or updated HP definitions.
according to either the original or updated HP definitions.
Recall that parts (c) and (d) of Theorem 2.2.3 show that if X = x is not a cause of φ according to the original HP definition, then it is not part of a cause according to the updated HP definition. Example 2.8.1 shows that the converse is not true in general. Theorem 4.3.1 suggests that, by adding extra variables appropriately, we can construct a model where X = x is a cause of φ according to the original HP definition iff it is a cause according to the updated HP definition. As I mentioned earlier, this gives the original HP definition some technical advantages. With the original HP definition, causes are always single conjuncts; as Example 2.8.2 shows, this is not in general the case with the updated definition. (Many other examples show that it is not the case with the modified HP definition either.) Moreover, as I discuss in Section 5.3, testing for causality is harder for the updated HP definition (and the modified HP definition) than it is for the original HP definition.
But adding extra variables so as to avoid the use of AC2(bu) may result in a rather “unnatural” model (of course, this presumes that we can agree on what “natural” means!). Moreover, as I mentioned earlier, in some cases it does not seem appropriate to add these variables (see Chapter 8). More experience is needed to determine which of AC2(bu) and AC2(bo) is most appropriate or whether (as I now suspect) using the modified HP definition is the right thing to do. Fortunately, in many cases, the causality judgment is independent of which we use.
4.4 The Stability of (Non-)Causality
The examples in Section 4.1 raise a potential concern. Consider the rock-throwing example again. Adding extra variables changed BT = 1 from being a cause of BS = 1 to not being a cause. Could adding even more variables convert BT = 1 back to being a cause? Could it then alternate further?
Indeed it can, at least in the case of the original and updated HP definition. In general, we can convert an event from being a cause to a non-cause and then back again infinitely often by adding variables. We have essentially already seen this in the bogus prevention problem. Suppose that we just start with Bodyguard, who puts the antidote in the victim’s coffee. To start with, there is no assassin, so surely Bodyguard putting in the antidote is not a cause of the victim surviving. Now we introduce an assassin. Since there will be a number of potential assassins, call this first assassin Assassin #1. Assassin #1 is not a serious assassin. Although in principle he could put in poison, and has toyed with the idea, in fact, he does not. As we have seen, just the fact that he could put in poison is enough to make Bodyguard putting in the antidote a cause of Victim surviving according to the original and updated HP definition and part of a cause according to the modified definition. But, as we also saw in Section 3.4, once we add a variable PN1 that talks about whether the poison was neutralized by the antidote, Bodyguard is no longer a cause.
Now we can repeat this process. Suppose that we discover that there is a second assassin, Assassin #2. Now Bodyguard putting in the antidote becomes (part of) a cause again; add PN2, and it is no longer a cause. This can go on arbitrarily often.
I now formalize this. Specifically, I construct a sequence M0, M1, M2,… of causal models and a context u such that Mn+1 is a conservative extension Mn for all n ≥ 0, B = 1 is not part of a cause of VS = 1 in the even-numbered models in context u, and B = 1 is part of a cause of VS = 1 in the odd-numbered models in context u. That is, the answer to the question “Is B = 1 part of a cause of VS = 1?” alternates as we go along the sequence of models.
M0 is just the model with two binary endogenous variables B and VS and one binary exogenous variable U. The values of both B and VS are determined by the context: in the context uj where U = j, B = VS = j, for j ∈ {0, 1}. The models M1, M2, M3,… are defined inductively. For n ≥ 0, we get M2n+1 from M2n by adding a new variable An+1; we get M2n+2 from M2n+1 by adding a new variable PN n+1. Thus, the model M2n+1 has the endogenous variables B, VS, A1,…, An+1, PN1,…, PNn; the model M2n+2 has the endogenous variables B, VS, A1,…, An+1, PN1,…, PNn+1. All these models have just one binary exogenous variable U. The exogenous variable determines the value of B and A1,…, An+1 in models M2n+1 and M2n+2; in the context u1, these variables all have value 1. In the context u0, these variables all have value 0; in addition, the equations are such that in u0, VS = 0 no matter how the other variables are set. Poor Victim has a terminal illness in u0, so does not survive no matter what else happens. The equation for PNj in all the models where it is a variable (namely, M2j, M2j+1,…) is just the analogue of the equation for PN in the original bogus prevention problem in Section 3.4.1:
![[image]](images/eqn3.jpg)
Assassin #j’s poison is neutralized if he actually puts poison in the coffee (recall Aj = 0 means that assassin #j puts poison in the coffee) and B puts in antidote. Finally, for VS, the equation depends on the model. In all cases, in u0, VS = 0; in u1,
Note that in M1, VS = A1 B, and in M2, VS = A1 PN1, so M1 and M2 are essentially the two models that were considered in Section 3.4.1.
The following theorem, whose proof can be found in Section 4.8.3, summarizes the situation with regard to the models M0, M1, M2, … defined above.
Theorem 4.4.1 For all n ≥ 0, Mn+1 is a conservative extension of Mn. Moreover, B = 1 is not part of a cause of VS = 1 in (M2n, u1), and B = 1 is part of a cause of VS = 1 in (M2n+1, u1), for n = 0, 1, 2, … (according to all variants of the HP definition).
Theorem 4.4.1 is somewhat disconcerting. It seems that looking more and more carefully at a situation should not result in our view of X = x being a cause of Y = y alternating between “yes” and “no”, at least not if we do not discover anything inconsistent with our understanding of the relations between previously known variables. Yet, Theorem 4.4.1 shows that this can happen. Moreover, the construction used in Theorem 4.4.1 can be applied to any model M such that![[image]](images/dclimg0060.jpg) , but B and C are independent of each other (so that, in particular, B = 1 is not a cause of C = 1), to get a sequence of models M0, M1,…, with M = M0 and Mn+1 a conservative extension of Mn such that the truth of the statement “B = 1 is part of a cause of C = 1 in
, but B and C are independent of each other (so that, in particular, B = 1 is not a cause of C = 1), to get a sequence of models M0, M1,…, with M = M0 and Mn+1 a conservative extension of Mn such that the truth of the statement “B = 1 is part of a cause of C = 1 in ![[image]](images/dclimg0061.jpg) ” alternates as we go along the sequence.
” alternates as we go along the sequence.
While disconcerting, I do not believe that, in fact, this is a serious problem. First, it is worth observing that while Theorem 4.4.1 applies to the original and updated HP definition even for (full) causes (this is immediate from the proof), with the modified definition, the fact that we are considering parts of causes rather than (full) causes is critical. Indeed, the following result is almost immediate from the definition of conservative extension.
Theorem 4.4.2 If M′ is a conservative extension of M, and ![[image]](images/dclimg0062.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dclimg0063.jpg) according to the modified HP definition, then there exists a (not necessarily strict) subset
according to the modified HP definition, then there exists a (not necessarily strict) subset ![[image]](images/dclimg0064.jpg) of
of ![[image]](images/dclimg0065.jpg) such that
such that ![[image]](images/dclimg0066.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dclimg0067.jpg) , where
, where ![[image]](images/dclimg0068.jpg) is the restriction of
is the restriction of ![[image]](images/dclimg0069.jpg) to the variables in
to the variables in ![[image]](images/dclimg0070.jpg) .
.
Proof: Suppose that ![[image]](images/dclimg0071.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dclimg0072.jpg) according to the modified HP definition. Then (a)
according to the modified HP definition. Then (a) ![[image]](images/dclimg0073.jpg) and (b) there exists a set
and (b) there exists a set ![[image]](images/dclimg0074.jpg) of endogenous variables and a setting
of endogenous variables and a setting ![[image]](images/dclimg0075.jpg) of the variables in
of the variables in ![[image]](images/dclimg0076.jpg) a setting
a setting ![[image]](images/dclimg0077.jpg) of the variables in
of the variables in ![[image]](images/dclimg0078.jpg) such that
such that ![[image]](images/dclimg0079.jpg) and
and ![[image]](images/dclimg0080.jpg) . (Part (b) is just the statement of AC2(am).) Since M′ is a conservative extension of M, (a) and (b) hold with M replaced by M′. So the only way that
. (Part (b) is just the statement of AC2(am).) Since M′ is a conservative extension of M, (a) and (b) hold with M replaced by M′. So the only way that ![[image]](images/dclimg0081.jpg) can fail to be a cause of φ in
can fail to be a cause of φ in ![[image]](images/dclimg0082.jpg) is if it fails AC3, which means that there must be a strict subset of
is if it fails AC3, which means that there must be a strict subset of ![[image]](images/dclimg0083.jpg) of
of ![[image]](images/dclimg0084.jpg) such that
such that ![[image]](images/dclimg0085.jpg) is a cause of φ. ■
is a cause of φ. ■
Thus, for the modified HP definition, for causes involving a single variable, causality is stable. For causes involving several conjuncts, we can get some instability, but not too much. It follows from Theorem 4.4.2 that we can get at most one alternation from non-causality to causality to non-causality. Once ![[image]](images/eqn4.jpg) goes from being a cause of φ in
goes from being a cause of φ in ![[image]](images/dclimg0086.jpg) to being a non-cause in (M′,
to being a non-cause in (M′, ![[image]](images/eqn5.jpg) ), it cannot go back to being a cause again in (M″,
), it cannot go back to being a cause again in (M″, ![[image]](images/eqn6.jpg) ) for a conservative extension M″ of M′ (since then
) for a conservative extension M″ of M′ (since then ![[image]](images/eqn7.jpg) is a cause of φ in (M′,
is a cause of φ in (M′, ![[image]](images/eqn8.jpg) ) for some strict subset
) for some strict subset ![[image]](images/eqn9.jpg) of
of ![[image]](images/eqn10.jpg) , so there must be a (not necessarily strict) subset
, so there must be a (not necessarily strict) subset ![[image]](images/eqn11.jpg) of
of ![[image]](images/eqn12.jpg) such that
such that ![[image]](images/eqn13.jpg) is a cause of φ in (M″, u). Thus, by AC3,
is a cause of φ in (M″, u). Thus, by AC3, ![[image]](images/eqn14.jpg) cannot be a cause of φ in (M″, u).)
cannot be a cause of φ in (M″, u).)
The rock-throwing example shows that we can have a little alternation. Suzy’s throw (ST = 1) is not a cause of the bottle shattering in the naive rock-throwing model MRT in the context where both Billy and Suzy throw; rather, according to the modified HP definition, ST = 1 ∧ BT = 1 is a cause, so Suzy’s throw in only part of a cause. In contrast, Suzy’s throw is a cause in the more sophisticated rock-throwing model. But it follows from Theorem 4.4.2 that Suzy’s throw will continue to be a cause of the bottle shattering in any conservative extension of the sophisticated rock-throwing model according to the modified HP definition. More generally, arguably, stability is not a problem for full causality using the modified HP definition.
But even according to the original and updated HP definition, and for parts of causes with the modified HP definition, I don’t think that the situation is so dire. A child may start with a primitive understanding of how the world works and believe that just throwing a rock causes a bottle to shatter. Later he may become aware of the importance of the rock actually hitting the bottle. Still later, he may become aware of other features critical to bottles shattering. This increased awareness can and should result in causality ascriptions changing. However, in practice, there are very few new features that should matter. We can make this precise by observing that most new features that we become aware of are almost surely irrelevant to the bottle shattering, except perhaps in highly abnormal circumstances. If the new variables were relevant, we probably would have become aware of them sooner. The fact that we don’t become aware of them suggests that we need to use an abnormal setting of these variables to uncover the causality.
As I now show, once we take normality into account, under reasonable assumptions, non-causality is stable. To make this precise, I must first extend the notion of conservative extension to extended causal models so as to take the normality ordering into account. For definiteness, I use the definitions in Section 3.2, where normality is defined on worlds, rather than the alternative definition in Section 3.5, although essentially the same arguments work in both cases. I do make some brief comments throughout about the modifications needed to deal with the alternative definition.
Definition 4.4.3 An extended causal model ![[image]](images/eqn15.jpg) is a conservative extension of an extended causal model
is a conservative extension of an extended causal model ![[image]](images/eqn16.jpg) if the causal model
if the causal model ![[image]](images/eqn17.jpg) underlying M′ is a conservative extension of the causal model
underlying M′ is a conservative extension of the causal model ![[image]](images/eqn18.jpg) underlying M according to Definition 4.2.1 and, in addition, the following condition holds, where
underlying M according to Definition 4.2.1 and, in addition, the following condition holds, where ![[image]](images/eqn19.jpg) is the set of endogenous variables in M:
is the set of endogenous variables in M:
CE. For all contexts ![[image]](images/eqn20.jpg) , if
, if ![[image]](images/eqn21.jpg) , then
, then ![[image]](images/eqn22.jpg) .
.
■
Roughly speaking, CE says that the normality ordering when restricted to worlds characterized by settings of the variables in ![[image]](images/eqn23.jpg) is the same in M and M′. (Actually, CE says less than this. I could have taken a stronger version of CE that would be closer to this English gloss: if
is the same in M and M′. (Actually, CE says less than this. I could have taken a stronger version of CE that would be closer to this English gloss: if ![[image]](images/eqn24.jpg) , then
, then ![[image]](images/eqn25.jpg) iff
iff ![[image]](images/eqn26.jpg) . The version of CE that I consider suffices to prove the results below, but this stronger version seems reasonable as well.) With the alternative definition, where the normality ordering is on contexts, the analogue of CE is even simpler: it just requires that the normality ordering in M and M′ is identical (since the set of contexts is the same in both models).
. The version of CE that I consider suffices to prove the results below, but this stronger version seems reasonable as well.) With the alternative definition, where the normality ordering is on contexts, the analogue of CE is even simpler: it just requires that the normality ordering in M and M′ is identical (since the set of contexts is the same in both models).
For the remainder of this section, I work with extended causal models M and M′ and use the definition of causality that takes normality into account (i.e., I use AC2+(a) for the original and updated definition and use AC2+(am) for the modified definition), although, for ease of exposition, I do not mention this explicitly. As above, I take ⪰ and ⪰′ to be the preorders in M and M′, respectively.
Note that Theorem 4.4.2 applies to the modified HP definition even for extended causal models. Thus, again, stability is not a serious problem for the modified HP definition in extended causal models. I now provide a condition that almost ensures that non-causality is stable for all the versions of the HP definition. Roughly speaking, I want it to be abnormal for a variable to take on a value other than that specified by the equations. Formally, say that in world s, V takes on a value other than that specified by the equations in ![[image]](images/dclimg0087.jpg) if, taking
if, taking ![[image]](images/eqn27.jpg) to consist of all endogenous variables in M other than V, if
to consist of all endogenous variables in M other than V, if ![[image]](images/eqn28.jpg) gives the values of the variables in
gives the values of the variables in ![[image]](images/eqn29.jpg) in s, and v is the value of V in s, then
in s, and v is the value of V in s, then ![[image]](images/eqn30.jpg) . For future reference, note that it is easy to check that if
. For future reference, note that it is easy to check that if ![[image]](images/eqn31.jpg) and
and ![[image]](images/eqn32.jpg) , then V takes on a value other than that specified by the equations in
, then V takes on a value other than that specified by the equations in ![[image]](images/eqn33.jpg) . The normality ordering in M respects the equations for V relative to
. The normality ordering in M respects the equations for V relative to ![[image]](images/eqn34.jpg) if, for all worlds s such that V takes on a value in s other than that specified by the equations in
if, for all worlds s such that V takes on a value in s other than that specified by the equations in ![[image]](images/dclimg0088.jpg) , we have
, we have ![[image]](images/eqn35.jpg) (where ⪰ is the preorder on worlds in M). Using the alternative definition of normality, there is an analogous condition: if
(where ⪰ is the preorder on worlds in M). Using the alternative definition of normality, there is an analogous condition: if ![[image]](images/eqn36.jpg) is a context where V takes on a value different from that specified by the equations in
is a context where V takes on a value different from that specified by the equations in ![[image]](images/dclimg0089.jpg) , then we have
, then we have ![[image]](images/eqn37.jpg) . Since the normality ordering on contexts is the same in M and M′, this means that unless
. Since the normality ordering on contexts is the same in M and M′, this means that unless ![[image]](images/eqn38.jpg) , the value that V takes on in context
, the value that V takes on in context ![[image]](images/eqn39.jpg) in M′ must be that specified by the equations in
in M′ must be that specified by the equations in ![[image]](images/dclimg0090.jpg) .
.
To show that B = 1 is a cause of VS = 1 in (M2n+1, u1), we consider a witness s where An+1 = 0. If we assume that the normality ordering in M2n+1 respects the equations for An+1 relative to u1, then s is less normal than ![[image]](images/eqn40.jpg) , so cannot be used to satisfy AC2+(a) or AC2+(am) when we are considering causality in (M, u1). As a consequence, it follows that B = 1 is not a cause of VS = 1 in M2n+1 under this assumption. More generally, as I now show, if the normality ordering respects the equations for all the variables added in going from M to a conservative extension M′ relative to
, so cannot be used to satisfy AC2+(a) or AC2+(am) when we are considering causality in (M, u1). As a consequence, it follows that B = 1 is not a cause of VS = 1 in M2n+1 under this assumption. More generally, as I now show, if the normality ordering respects the equations for all the variables added in going from M to a conservative extension M′ relative to ![[image]](images/eqn41.jpg) , then causality in
, then causality in ![[image]](images/dclimg0091.jpg) is stable. Exactly how stable it is depends in part on the variant of the HP definition considered. The next theorem gives the key result.
is stable. Exactly how stable it is depends in part on the variant of the HP definition considered. The next theorem gives the key result.
Theorem 4.4.4 Suppose that M and M′ are extended causal models such that M′ is a conservative extension of M, the normality ordering in M′ respects the equations for all variables in ![[image]](images/eqn42.jpg) relative to
relative to ![[image]](images/eqn43.jpg) , where
, where ![[image]](images/eqn44.jpg) and
and ![[image]](images/eqn45.jpg) are the sets of endogenous variables in M and M′, respectively, and all the variables in φ are in
are the sets of endogenous variables in M and M′, respectively, and all the variables in φ are in ![[image]](images/eqn46.jpg) . Then the following holds:
. Then the following holds:
(a)According to the original and updated HP definition, if ![[image]](images/eqn47.jpg) is not a cause of φ in
is not a cause of φ in ![[image]](images/dclimg0092.jpg) , then either
, then either ![[image]](images/eqn48.jpg) is not a cause of φ in (M′,
is not a cause of φ in (M′, ![[image]](images/eqn49.jpg) ) or there is a strict subset
) or there is a strict subset ![[image]](images/eqn50.jpg) of
of ![[image]](images/eqn51.jpg) such that
such that ![[image]](images/eqn52.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dclimg0093.jpg) , where
, where ![[image]](images/eqn53.jpg) is the restriction of
is the restriction of ![[image]](images/eqn54.jpg) to the variables in
to the variables in ![[image]](images/eqn55.jpg) .
.
(b)According to the modified HP definition, ![[image]](images/eqn56.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dclimg0094.jpg) iff
iff ![[image]](images/eqn57.jpg) is a cause of φ in (M′,
is a cause of φ in (M′, ![[image]](images/eqn58.jpg) ) (so, in particular, a cause of φ in (M′,
) (so, in particular, a cause of φ in (M′, ![[image]](images/eqn59.jpg) ) cannot involve a variable in
) cannot involve a variable in ![[image]](images/eqn60.jpg) ).
).
It is immediate from part (b) that, under the assumptions of Theorem 4.4.4, both causality and non-causality are stable for the modified HP definition. It is also immediate from part (a) that, for the original and updated HP definition, non-causality is stable for causes that are single conjuncts. I believe that for the original HP definition, non-causality is stable even for causes that are not single conjuncts (recall that with the original HP definition, there can be causes that are not single conjuncts once we take normality into account; see Example 3.2.3), although I have not yet proved this. However, for the updated HP definition, non-causality may not be stable for conjuncts that are not single conjuncts (see Example 4.8.2 below). But we cannot get too much alternation. Given the appropriate assumptions about the normality ordering, the following result shows that ![[image]](images/eqn61.jpg) cannot go from being a cause of φ to not being a cause back to being a cause again according to the original and updated HP definition; if we have three models M, M′, and M″, where M′ is a conservative extension of M, M″ is a conservative extension of M′, and
cannot go from being a cause of φ to not being a cause back to being a cause again according to the original and updated HP definition; if we have three models M, M′, and M″, where M′ is a conservative extension of M, M″ is a conservative extension of M′, and ![[image]](images/eqn62.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dclimg0095.jpg) and (M″,
and (M″, ![[image]](images/eqnl59.jpg) ), then
), then ![[image]](images/eqn64.jpg) must also be a cause of φ in (M′,
must also be a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ).
).
Theorem 4.4.5 According to the original and updated HP definition, if (a) M′ is a conservative extension of M, (b) M″ is a conservative extension of M′, (c) ![[image]](images/eqn66.jpg) ) is a cause of φ in
) is a cause of φ in ![[image]](images/dclimg0096.jpg) and (M″,
and (M″, ![[image]](images/eqn67.jpg) ), (d) the normality ordering in M′ respects the equations for all endogenous variables in M′ not in M relative to
), (d) the normality ordering in M′ respects the equations for all endogenous variables in M′ not in M relative to ![[image]](images/eqn68.jpg) ), and (e) the normality ordering in M″ respects the equations for all endogenous variables in M″ not in M′ relative to --u, then
), and (e) the normality ordering in M″ respects the equations for all endogenous variables in M″ not in M′ relative to --u, then ![[image]](images/eqn69.jpg) is also a cause of φ in (M′,
is also a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ).
).
Although these results show that we get stability of causality, it comes at a price, at least in the case of the original and updated HP definition: the assumption that the normality ordering respects the equations for a variable relative to a context ![[image]](images/eqn68.jpg) is clearly quite strong. For one thing, for the modified HP definition, it says that there are no “new” causes of φ in (M′,
is clearly quite strong. For one thing, for the modified HP definition, it says that there are no “new” causes of φ in (M′, ![[image]](images/eqn68.jpg) ) that involve variables that were added in going from M to M′. Very roughly speaking, the reason is the following: Because the normality ordering respects the equations in
) that involve variables that were added in going from M to M′. Very roughly speaking, the reason is the following: Because the normality ordering respects the equations in ![[image]](images/eqn68.jpg) , not only are all the new variables that are added determined by the original variables, under normal conditions, in context
, not only are all the new variables that are added determined by the original variables, under normal conditions, in context ![[image]](images/eqn68.jpg) , the new variables have no impact on the original variables beyond that already determined in
, the new variables have no impact on the original variables beyond that already determined in ![[image]](images/dclimg0097.jpg) .
.
Although it may seem reasonable to require that it be abnormal for the new variables not to respect the equations in ![[image]](images/eqn68.jpg) , recall the discussion after Example 3.2.6: the normality ordering is placed on worlds, which are complete assignments to the endogenous variables, not on complete assignments to both endogenous and exogenous variables. Put another way, in general, the normality ordering does not take the context into account. So saying that the normality ordering respects the equations for a variable V relative to
, recall the discussion after Example 3.2.6: the normality ordering is placed on worlds, which are complete assignments to the endogenous variables, not on complete assignments to both endogenous and exogenous variables. Put another way, in general, the normality ordering does not take the context into account. So saying that the normality ordering respects the equations for a variable V relative to ![[image]](images/eqn68.jpg) is really saying that, as far as V is concerned, what happens in
is really saying that, as far as V is concerned, what happens in ![[image]](images/eqn68.jpg) is really the normal situation. Obviously, how reasonable this assumption is depends on the example.
is really the normal situation. Obviously, how reasonable this assumption is depends on the example.
To see that it is not completely unreasonable, consider the assassin example used to prove Theorem 4.4.1. It might be better to think of the variable An in this example as being three-valued: An = 0 if assassin #n is present and puts in poison, An = 1 if assassin #n is present and does not put in poison, and An = 2 if assassin #n is not present. Clearly the normal value is An = 2. Take u to be the context where, in model M2n+1, An = 2. While the potential presence a number of assassins makes bodyguard putting in antidote (part of) a cause in (M2n+1, u), it is no longer part of a cause once we take normality into account. Moreover, here it does seem reasonable to say that violating the equations for An relative to u is abnormal.
These observations suggest why, in general, although the assumption that the normality ordering respects the equations for the variables in ![[image]](images/eqn60.jpg) relative to the context
relative to the context ![[image]](images/eqn68.jpg) is a strong one, it may not be so unreasonable in practice. Typically, the variables that we do not mention take on their expected values, and thus are not even noticed.
is a strong one, it may not be so unreasonable in practice. Typically, the variables that we do not mention take on their expected values, and thus are not even noticed.
Theorem 4.4.4 is the best we can do. In Section 4.8.3, I give an example showing that it is possible for ![[image]](images/eqn62.jpg) to go from being a non-cause of φ to being a cause to being a non-cause again according to the original and updated definition, even taking normality into account. (By Theorem 4.4.5, it must then stay a non-cause.)
to go from being a non-cause of φ to being a cause to being a non-cause again according to the original and updated definition, even taking normality into account. (By Theorem 4.4.5, it must then stay a non-cause.)
There is one other issue to consider: can X = x alternate from being part of a cause of φ infinitely often, even if we take normality considerations into account? In the case of the modified HP definition, it follows easily from Theorem 4.4.4 that the answer is no.
Theorem 4.4.6 Suppose that M and M′ are extended causal models such that M′ is a conservative extension of M, and the normality ordering in M′ respects the equations for all variables in ![[image]](images/eqn60.jpg) relative to
relative to ![[image]](images/eqn68.jpg) , where
, where ![[image]](images/eqn46.jpg) and
and ![[image]](images/eqn45.jpg) are the sets of endogenous variables in M and M′, respectively. Then X = x is part of a cause of φ in
are the sets of endogenous variables in M and M′, respectively. Then X = x is part of a cause of φ in ![[image]](images/dclimg0098.jpg) according to the modified HP definition iff X = x is part of a cause of φ in (M′,
according to the modified HP definition iff X = x is part of a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ) according to the modified HP definition.
) according to the modified HP definition.
Proof: If X = x is part of a cause ![[image]](images/eqn62.jpg) of φ in (M, u) according to the modified HP definition, then by Theorem 4.4.4(b),
of φ in (M, u) according to the modified HP definition, then by Theorem 4.4.4(b), ![[image]](images/eqn62.jpg) is a cause of φ in (M′, u), and hence X = x is part of a cause in (M′, u). Conversely, if X = x is part of a cause
is a cause of φ in (M′, u), and hence X = x is part of a cause in (M′, u). Conversely, if X = x is part of a cause ![[image]](images/eqn62.jpg) in (M′, u), then by Theorem 4.4.4(b) again, all the variables in
in (M′, u), then by Theorem 4.4.4(b) again, all the variables in ![[image]](images/eqn51.jpg) are in
are in ![[image]](images/eqn46.jpg) , and
, and ![[image]](images/eqn62.jpg) is a cause of φ in (M, u), so X = x is part of a cause in (M, u). ■
is a cause of φ in (M, u), so X = x is part of a cause in (M, u). ■
I conjecture that, under the assumptions of Theorem 4.4.6, if X = x is not part of a cause in (M, u) according to the updated HP definition, then it is not part of a cause according to the original or updated HP definition in (M′, u) either, but I have not been able to prove this.
One final point is worth making. Recall that the model ![[image]](images/eqn92.jpg) is not a conservative ex- tension of MRT and
is not a conservative ex- tension of MRT and ![[image]](images/eqn93.jpg) . The addition of the variables SA, BA, SF, and BF makes the contexts in the two models fundamentally different. Yet, in the context u∗ in
. The addition of the variables SA, BA, SF, and BF makes the contexts in the two models fundamentally different. Yet, in the context u∗ in ![[image]](images/eqn94.jpg) where the same assumptions are made as in
where the same assumptions are made as in ![[image]](images/eqn95.jpg) and MRT, namely, that Suzy and Billy both throw, are both accurate, and Suzy hits first, we have the same causality ascriptions. This is not a fluke. In Definition 4.2.1, conservative extension is defined as a relation between two models. We can also define what it means for one causal setting (M′, u′) to be a conservative extension of another causal setting (M, u). The set of endogenous variables in M is still required to be a subset of that in M′, but now we can drop the requirement that M and M′ use the same exogenous variables.
and MRT, namely, that Suzy and Billy both throw, are both accurate, and Suzy hits first, we have the same causality ascriptions. This is not a fluke. In Definition 4.2.1, conservative extension is defined as a relation between two models. We can also define what it means for one causal setting (M′, u′) to be a conservative extension of another causal setting (M, u). The set of endogenous variables in M is still required to be a subset of that in M′, but now we can drop the requirement that M and M′ use the same exogenous variables.
Definition 4.4.7 Given causal models ![[image]](images/eqn96.jpg) and
and ![[image]](images/eqn97.jpg) , the setting
, the setting ![[image]](images/eqn98.jpg) is a conservative extension of
is a conservative extension of ![[image]](images/dclimg0099.jpg) if
if ![[image]](images/eqn99.jpg) , and for all contexts
, and for all contexts ![[image]](images/eqn100.jpg) , all variables
, all variables ![[image]](images/eqn101.jpg) , and all settings
, and all settings ![[image]](images/eqn102.jpg) of the variables in
of the variables in ![[image]](images/eqn103.jpg) , we have
, we have ![[image]](images/eqn104.jpg) . ■
. ■
It is easy to see that, although ![[image]](images/eqn94.jpg) is not a conservative extension of MRT or
is not a conservative extension of MRT or ![[image]](images/eqn95.jpg) , (
, (![[image]](images/eqn107.jpg) ) is a conservative extension of both (MRT, u) and (
) is a conservative extension of both (MRT, u) and (![[image]](images/eqn108.jpg) ).
).
We can further extend this definition to extended causal models by requiring that the condition CE holds when restricted to the two relevant settings. That is, if ![[image]](images/eqn109.jpg) , we require that
, we require that ![[image]](images/eqn110.jpg) . For the alternative definition, we can no longer require that the normality ordering on contexts be identical; the set of contexts is different in the two models. Rather, I require that the normality ordering works the same way on sets definable by formulas involving only variables in
. For the alternative definition, we can no longer require that the normality ordering on contexts be identical; the set of contexts is different in the two models. Rather, I require that the normality ordering works the same way on sets definable by formulas involving only variables in ![[image]](images/eqn46.jpg) . Formally, I require that for all Boolean combinations φ and φ′ of primitive events that involve only the endogenous variables in
. Formally, I require that for all Boolean combinations φ and φ′ of primitive events that involve only the endogenous variables in ![[image]](images/eqn46.jpg) , we have ⟦φ⟧⪰e ⟦φ′⟧ iff ⟦φ⟧ (⪰e)′ ⟦φ′⟧.
, we have ⟦φ⟧⪰e ⟦φ′⟧ iff ⟦φ⟧ (⪰e)′ ⟦φ′⟧.
All the results proved in this section on conservative extensions hold without change if we consider conservative extensions of causal settings, with just minimal changes to the proof. (I considered conservative extensions of causal models here only because the results are a little easier to state.) This helps explain why (![[image]](images/eqn113.jpg) ) and (
) and (![[image]](images/eqn114.jpg) ) are the same as far as causality ascriptions go.
) are the same as far as causality ascriptions go.
As I said earlier, the set of possible values of a variable must also be chosen carefully. The appropriate set of values of a variable will depend on the other variables in the picture and the relationship between them. Suppose, for example, that a hapless homeowner comes home from a trip to find that his front door is stuck. If he pushes on the door with normal force, then it will not open. However, if he leans his shoulder against it and gives a solid push, then the door will open. To model this, it suffices to have a variable O with values either 0 or 1, depending on whether the door opens, and a variable P, with values 0 or 1 depending on whether the homeowner gives a solid push.
In contrast, suppose that the homeowner also forgot to disarm the security system and the system is very sensitive, so it will be tripped by any push on the door, regardless of whether the door opens. Let A = 1 if the alarm goes off, A = 0 otherwise. Now if we try to model the situation with the same variable P, we will not be able to express the dependence of the alarm on the homeowner’s push. To deal with both O and A, we need to extend P to a 3-valued variable P′, with values 0 if the homeowner does not push the door, 1 if he pushes it with normal force, and 2 if he gives it a solid push.
Although in most cases, a reasonable choice for the range of the variables in a model is not hard to come by, there are some important independence principles that apply. That is the topic of the next section.
4.6 Dependence and Independence
The whole notion of intervention requires that we be able to set variables independently. This means that values of different variables should not correspond to logically related events. For suppose that we had a model with variable H1 and H2, where H1 represents “Martha says ‘hello’ ” (i.e., H1 = 1 if Martha says “hello” and H1 = 0 otherwise), and H2 represents “Martha says ‘hello’ loudly”. The intervention H1 = 0 ∧ H2 = 1 is meaningless; it is logically impossible for Martha not to say “hello” and to say “hello” loudly.
For this reason, I was careful to say in the examples in Section 4.1 that the variables added to help in structuring the scenarios were independent variables, not ones defined in terms of the original variables. Thus, for example, the variable D that was added in Example 4.1.1, whose equation is given as D = ¬S ∧ A, can be thought of as a switch that turns on if S makes the route from A to C active and A is on; in particular, it can be set to 1 even if, say, A is off.
It is unlikely that a careful modeler would choose variables that have logically related values. However, the converse of this principle, that the different values of any particular variable should be logically related (in particular, mutually exclusive), is less obvious and equally important. Consider Example 2.3.3. Although, in the actual context, Billy’s rock will hit the bottle if Suzy’s doesn’t, this is not a necessary relationship. Suppose that, instead of using two variables SH and BH, we try to model the scenario with a variable H that takes the value 1 if Suzy’s rock hits and 0 if Billy’s rock hits. If BS = 1 no matter who hits the bottle (i.e., no matter what the value of H), then it is not hard to verify that in this model, there is no contingency such that the bottle’s shattering depends on Suzy’s throw. The problem is that H = 0 and H = 1 are not mutually exclusive; there are possible situations in which both rocks hit or neither rock hits the bottle. Using the language from earlier in this chapter, this model is insufficiently expressive; there are situations significant to the analysis that cannot be represented. In particular, in this model, we cannot consider independent interventions on the rocks hitting the bottle. As the discussion in Example 2.3.3 shows, it is precisely such an intervention that is needed to establish that Suzy’s throw (and not Billy’s) is the actual cause of the bottle shattering.
Although these rules are simple in principle, their application is not always transparent. For example, they will have particular consequences for how we should represent events that might occur at different times. Consider the following example.
Example 4.6.1 Suppose that the Careless Camper (CC for short) has plans to go camping on the first weekend in June. He will go camping unless there is a fire in the forest in May. If he goes camping, he will leave a campfire unattended, and there will be a forest fire. Let the variable C take the value 1 if CC goes camping and 0 otherwise. How should the state of the forest be represented?
There appear to be at least three alternatives. The simplest proposal would be to use a variable F that takes the value 1 if there is a forest fire at some time and 0 otherwise. But in that case, how should the dependency relations between F and C be represented? Since CC will go camping only if there is no fire (in May), we would want to have an equation such as C = ¬F. However, since there will be a fire (in June) iff CC goes camping, we would also need F = C. This representation is clearly not expressive enough, since it does not let us make the clearly relevant distinction between whether the forest fire occurs in May or June. As a consequence, the model is not recursive, and the equations have no consistent solution. A second alternative would be to use a variable F′ that takes the value 0 if there is no fire, 1 if there is a fire in May, and 2 if there is a fire in June. But now how should the equations be written? Since CC will go camping unless there is a fire in May, the equation for C should say that C = 0 iff F′ = 1. And since there will be a fire in June if CC goes camping, the equation for F′ should say that F′ = 2 if C = 1. These equations are highly misleading in what they predict about the effects of interventions. For example, the first equation tells us that intervening to create a forest fire in June would cause CC to go camping in the beginning of June. But this seems to get the causal order backward!
The third way to model the scenario is to use two separate variables, F1 and F2, to represent the state of the forest at separate times. F1 = 1 will represent a fire in May, and F1 = 0 represents no fire in May; F2 = 1 represents a fire in June and F2 = 0 represents no fire in June. Now we can write our equations as C = 1 − F1 and F2 = C × (1 − F1). This representation is free from the defects that plague the other two representations. We have no cycles, and hence there will be a consistent solution for any value of the exogenous variables. Moreover, this model correctly tells us that only an intervention on the state of the forest in May will affect CC’s camping plans. ■
The problem illustrated in this example could also arise in Example 2.4.1. Recall that in that example, there was a variable BMC that represented Billy’s medical condition, with possible values 0 (Billy feels fine on both Tuesday and Wednesday), 1 (Billy feels sick Tuesday morning and fine Wednesday), 2 (Billy feels sick both Tuesday and Wednesday), and 3 (Billy feels fine Tuesday and is dead on Wednesday). Now suppose that we change the story so that the second dose has no impact, but if Billy feels fine on Tuesday, he will do a dangerous stunt dive on Wednesday and die. If we add a variable SD that captures whether Billy does a stunt dive, then SD = 1 if BMC is either 0 or 3 and BMC = 3 if SD = 1; again we get circularity. What this shows is that the problem is due to the combination of having a causal model with a variable X whose values correspond to different times together with another variable causally “sandwiched” between the different values of X.
Similarly, the first representation suggested in Example 4.6.1 is inappropriate only because it is important for the example when the fire occurs. The model would be insufficiently expressive unless it could capture that. However, if the only effect of the forest fire that we are considering is the level of tourism in August, then the first representation may be perfectly adequate. Since a fire in May or June will have the same impact on August tourism, we need not distinguish between the two possibilities in our model.
All this shows that causal modeling can be subtle, especially with variables whose values are time dependent. The following example emphasizes this point.
Example 4.6.2 It seems that being born can be viewed as a cause of one’s death. After all, if one hadn’t been born, then one wouldn’t have died. But this sounds a little odd. If Jones dies suddenly one night, shortly before his 80th birthday, then the coroner’s inquest is unlikely to list “birth” as among the causes of his death. Typically, when we investigate the causes of death, we are interested in what makes the difference between a person’s dying and his surviving. So a model might include a variable D such that D = 1 holds if Jones dies shortly before his 80th birthday, and D = 0 holds if he continues to live. If the model also includes a variable B, taking the value 1 if Jones is born, 0 otherwise, then there simply is no value that D would take if B = 0. Both D = 0 and D = 1 implicitly presuppose that Jones was born (i.e., B = 1). Thus, if the model includes a variable such as D, then it should not also include B, and so we will not be able to conclude that Jones’s birth is a cause of his death! More generally, including the variable D in our model amounts to building in the presupposition that Jones exists and lives to be 79. Only variables whose values are compatible with that presupposition can be included in the model. ■
4.7 Dealing With Normality and Typicality
As we have seen, adding a normality theory to the model gives the HP definition greater flexibility to deal with many cases. This raises the worry, however, that this gives the modeler too much flexibility. After all, the modeler can now render any claim that A is an actual cause of B false by simply choosing a normality order that makes the actual world ![[image]](images/eqn115.jpg) more normal than any world s needed to satisfy AC2. Thus, the introduction of normality exacerbates the problem of motivating and defending a particular choice of model.
more normal than any world s needed to satisfy AC2. Thus, the introduction of normality exacerbates the problem of motivating and defending a particular choice of model.
There was a discussion in Chapter 3 about various interpretations of normality: statistical norms, prescriptive norms, moral norms, societal norms, norms that are dictated by policies (as in the Knobe-Fraser experiment), and norms of proper functioning. The law also suggests a variety of principles for determining the norms that are used in the evaluation of actual causation. In criminal law, norms are determined by direct legislation. For example, if there are legal standards for the strength of seat belts in an automobile, a seat belt that did not meet this standard could be judged a cause of a traffic fatality. By contrast, if a seat belt complied with the legal standard, but nonetheless broke because of the extreme forces it was subjected to during a particular accident, the fatality would be blamed on the circumstances of the accident, rather than the seat belt. In such a case, the manufacturers of the seat belt would not be guilty of criminal negligence. In contract law, compliance with the terms of a contract has the force of a norm. In tort law, actions are often judged against the standard of “the reasonable person”. For instance, if a bystander was harmed when a pedestrian who was legally crossing the street suddenly jumped out of the way of an oncoming car, the pedestrian would not be held liable for damages to the bystander, since he acted as the hypothetical “reasonable person” would have done in similar circumstances. There are also a number of circumstances in which deliberate malicious acts of third parties are considered to be “abnormal” interventions and affect the assessment of causation.
As with the choice of variables, I do not expect that these considerations will always suffice to pick out a uniquely correct theory of normality for a causal model. They do, however, provide resources for a rational critique of models.
Lemma 4.2.2: Suppose that M′ is a conservative extension of ![[image]](images/eqn116.jpg) . Then for all causal formulas φ that mention only variables in
. Then for all causal formulas φ that mention only variables in ![[image]](images/eqn117.jpg) and all contexts
and all contexts ![[image]](images/eqn68.jpg) , we have (M,
, we have (M, ![[image]](images/eqn68.jpg) ) ⊨ φ iff (M′,
) ⊨ φ iff (M′, ![[image]](images/eqnl59.jpg) ) ⊨ φ.
) ⊨ φ.
Proof: Fix a context ![[image]](images/eqn68.jpg) . Since M is a recursive model, there is some partial order
. Since M is a recursive model, there is some partial order ![[image]](images/eqn122.jpg) on the endogenous variables such that unless
on the endogenous variables such that unless ![[image]](images/eqn123.jpg) , Y is not affected by X in context
, Y is not affected by X in context ![[image]](images/eqn124.jpg) ; that is, unless X
; that is, unless X ![[image]](images/eqn125.jpg) Y, if the exogenous variables are set to
Y, if the exogenous variables are set to ![[image]](images/eqn68.jpg) , then changing the value of X has no impact on the value of Y according to the structural equations in M, no matter what the setting of the other endogenous variables. Say that X is independent of a set
, then changing the value of X has no impact on the value of Y according to the structural equations in M, no matter what the setting of the other endogenous variables. Say that X is independent of a set ![[image]](images/eqn127.jpg) of endogenous variables in
of endogenous variables in ![[image]](images/dclimg0100.jpg) if X is independent of Y in
if X is independent of Y in ![[image]](images/dclimg0101.jpg) for all
for all ![[image]](images/eqn128.jpg) .
.
Suppose that ![[image]](images/eqn129.jpg) . Since M is a recursive model, we can assume without loss of generality that these variables are ordered so that Xi is independent of {Xi+1,…, Xn} in
. Since M is a recursive model, we can assume without loss of generality that these variables are ordered so that Xi is independent of {Xi+1,…, Xn} in ![[image]](images/dclimg0102.jpg) for 1 ≤i ≤ n − 1. (Every set
for 1 ≤i ≤ n − 1. (Every set ![[image]](images/eqn45.jpg) of endogenous variables in a recursive model must contain a “minimal” element X such that it is not the case that
of endogenous variables in a recursive model must contain a “minimal” element X such that it is not the case that ![[image]](images/eqn131.jpg) . If such an element did not exist, we could create a cycle. Thus, X is independent of
. If such an element did not exist, we could create a cycle. Thus, X is independent of ![[image]](images/eqn132.jpg) in
in ![[image]](images/dclimg0103.jpg) . We construct the ordering by induction, finding Xi+1 by applying this observation to
. We construct the ordering by induction, finding Xi+1 by applying this observation to ![[image]](images/eqn133.jpg) I now prove by induction on j that, for all
I now prove by induction on j that, for all ![[image]](images/eqn134.jpg) all settings
all settings ![[image]](images/eqn135.jpg) of the variables in
of the variables in ![[image]](images/eqn136.jpg) , and all
, and all ![[image]](images/eqn137.jpg) , we have
, we have ![[image]](images/eqn138.jpg) iff
iff ![[image]](images/eqn139.jpg) : all interventions that make sense in both models produce the same results.
: all interventions that make sense in both models produce the same results.
For the base case of the induction, given ![[image]](images/eqn140.jpg) , let
, let ![[image]](images/eqn141.jpg) . Choose
. Choose ![[image]](images/eqn142.jpg) such that
such that ![[image]](images/eqn143.jpg) . Then we have
. Then we have
![[image]](images/eqn144.jpg)
This completes the proof of the base case. Suppose that 1 < j ≤ n and the result holds for 1,…, j − 1; I prove it for j. Given ![[image]](images/eqn149.jpg) now let
now let ![[image]](images/eqn150.jpg) , let
, let ![[image]](images/eqn151.jpg) , and let
, and let ![[image]](images/eqn152.jpg) . Thus,
. Thus, ![[image]](images/eqn153.jpg) consists of those variables that might affect Xj that are not already being intervened on (because they are in
consists of those variables that might affect Xj that are not already being intervened on (because they are in ![[image]](images/eqn154.jpg) ), whereas
), whereas ![[image]](images/eqn155.jpg) consists of those variables that do not affect Xj and are not already being intervened on. Since
consists of those variables that do not affect Xj and are not already being intervened on. Since ![[image]](images/eqn156.jpg) is contained in {Xj+1,…, Xn}, Xj is independent of
is contained in {Xj+1,…, Xn}, Xj is independent of ![[image]](images/eqn157.jpg) in
in ![[image]](images/dclimg0105.jpg) . Choose
. Choose ![[image]](images/eqn158.jpg) such that
such that ![[image]](images/eqn159.jpg) . Since
. Since ![[image]](images/eqn160.jpg) , by the induction hypothesis,
, by the induction hypothesis, ![[image]](images/eqn161.jpg) . By Lemma 2.10.2, we have
. By Lemma 2.10.2, we have ![[image]](images/eqn162.jpg) iff
iff ![[image]](images/eqn163.jpg) , and similarly for M′. Choose
, and similarly for M′. Choose ![[image]](images/eqn164.jpg) such that
such that ![[image]](images/eqn165.jpg) . Thus,
. Thus,
![[image]](images/eqn166.jpg)
This completes the proof of the inductive step.
It follows easily from the definition of ![[image]](images/eqn173.jpg) and
and ![[image]](images/eqn174.jpg) iff
iff ![[image]](images/eqn175.jpg) and similarly for M′. An easy induction shows that
and similarly for M′. An easy induction shows that ![[image]](images/eqn176.jpg) for an arbitrary Boolean combination ψ of primitive events that mentions only variables in
for an arbitrary Boolean combination ψ of primitive events that mentions only variables in ![[image]](images/eqn177.jpg) . Since causal formulas are Boolean combinations of formulas of the form
. Since causal formulas are Boolean combinations of formulas of the form ![[image]](images/eqn178.jpg) , another easy induction shows that (M,
, another easy induction shows that (M, ![[image]](images/eqn68.jpg) ) ⊨ ψ′ iff (M′,
) ⊨ ψ′ iff (M′, ![[image]](images/eqn68.jpg) ) ⊨ ψ′ for all causal formulas ψ′. ■
) ⊨ ψ′ for all causal formulas ψ′. ■
Theorem 4.3.1: If X = x is not a cause of Y = y in ![[image]](images/dclimg0107.jpg) according to the updated HP definition but is a cause according to the original HP definition, then there is a model M′ that is a conservative extension of M such that X = x is not a cause of Y = y in (M′,
according to the updated HP definition but is a cause according to the original HP definition, then there is a model M′ that is a conservative extension of M such that X = x is not a cause of Y = y in (M′, ![[image]](images/eqnl59.jpg) ) according to either the original or updated HP definitions.
) according to either the original or updated HP definitions.
Proof: Suppose that ![[image]](images/eqn182.jpg) is a witness to X = x being a cause of Y = y in
is a witness to X = x being a cause of Y = y in ![[image]](images/dclimg0108.jpg) according to the original HP definition. Let (M,
according to the original HP definition. Let (M, ![[image]](images/eqn68.jpg) ) ⊨
) ⊨ ![[image]](images/eqn185.jpg) . We must have
. We must have ![[image]](images/eqn186.jpg) , for otherwise it is easy to see that X = x would be a cause of Y = y in
, for otherwise it is easy to see that X = x would be a cause of Y = y in ![[image]](images/dclimg0109.jpg) according to the updated HP definition, with witness
according to the updated HP definition, with witness ![[image]](images/eqn187.jpg) .
.
If M′ is a conservative extension of M with additional variables ![[image]](images/eqn189.jpg) , say that
, say that ![[image]](images/eqn190.jpg) extends
extends ![[image]](images/eqn192.jpg) if
if ![[image]](images/eqn194.jpg) and
and ![[image]](images/eqn195.jpg) agrees with
agrees with ![[image]](images/eqn196.jpg) on the variables in
on the variables in ![[image]](images/eqn197.jpg) . I now construct a conservative extension M′ of M such that X = x is not a cause of Y = y in (M′,
. I now construct a conservative extension M′ of M such that X = x is not a cause of Y = y in (M′, ![[image]](images/eqn68.jpg) ) according to the original HP definition with a witness extending
) according to the original HP definition with a witness extending ![[image]](images/eqn199.jpg) . Of course, this just kills the witnesses in M′ that extend
. Of course, this just kills the witnesses in M′ that extend ![[image]](images/eqn199.jpg) . I then show that we can construct further conservative extensions of M to kill all other extensions of witnesses to X = x being a cause of Y = y in
. I then show that we can construct further conservative extensions of M to kill all other extensions of witnesses to X = x being a cause of Y = y in ![[image]](images/dclimg0110.jpg) according to the original HP definition.
according to the original HP definition.
Let M′ be obtained from M by adding one new variable NW. All the variables have the same equations in M and M′ except for Y and (of course) NW. The equations for NW are easy to explain: if X = x and ![[image]](images/eqn203.jpg) , then NW = 1; otherwise, NW = 0. The equations for Y are the same in M and M′ (and do not depend on the value of NW) except for two special cases. To define these cases, for each variable
, then NW = 1; otherwise, NW = 0. The equations for Y are the same in M and M′ (and do not depend on the value of NW) except for two special cases. To define these cases, for each variable ![[image]](images/eqn204.jpg) , if x″ ∈ {x, x′} define
, if x″ ∈ {x, x′} define ![[image]](images/eqn205.jpg) as the value such that
as the value such that ![[image]](images/eqn206.jpg) . That is,
. That is, ![[image]](images/eqn207.jpg) is the value taken by Z if X is set to x″ and
is the value taken by Z if X is set to x″ and ![[image]](images/eqn208.jpg) is set to
is set to ![[image]](images/eqn209.jpg) . Let
. Let ![[image]](images/eqn210.jpg) consist of all variables in
consist of all variables in ![[image]](images/eqn211.jpg) other than Y, let
other than Y, let ![[image]](images/eqn212.jpg) be a setting of the variables in
be a setting of the variables in ![[image]](images/eqn213.jpg) , and let
, and let ![[image]](images/eqn214.jpg) consist of all variables in
consist of all variables in ![[image]](images/eqn215.jpg) other than X. Then we want the equations for Y in M′ to be such that for all j ∈{0, 1}, we have
other than X. Then we want the equations for Y in M′ to be such that for all j ∈{0, 1}, we have
![[image]](images/eqn216.jpg)
unless the assignment ![[image]](images/eqn217.jpg) results in either (a) X = x,
results in either (a) X = x, ![[image]](images/eqn218.jpg) , for all
, for all ![[image]](images/eqn220.jpg) , and NW = 0 or (b)
, and NW = 0 or (b) ![[image]](images/eqn222.jpg) for all
for all ![[image]](images/eqn223.jpg) , and NW = 1. That is, the structural equations for Y are the same in M and M′ except for two special cases, characterized by (a) and (b). If (a) holds, Y = y′ in M′; if (b) holds, Y = y. Note that in both of these cases, the value of NW is “abnormal”. If X = x,
, and NW = 1. That is, the structural equations for Y are the same in M and M′ except for two special cases, characterized by (a) and (b). If (a) holds, Y = y′ in M′; if (b) holds, Y = y. Note that in both of these cases, the value of NW is “abnormal”. If X = x, ![[image]](images/eqn224.jpg) , and
, and ![[image]](images/eqn225.jpg) for all
for all ![[image]](images/eqn226.jpg) , then NW should be 1; if we set X to x′ and change the values of the variables in
, then NW should be 1; if we set X to x′ and change the values of the variables in ![[image]](images/eqn227.jpg) accordingly, then NW should be 0.
accordingly, then NW should be 0.
I now show that M′ has the desired properties and, in addition, does not make X = x a cause in new ways.
Lemma 4.8.1
(a)It is not the case that X = x is a cause of Y = y in (M′, ![[image]](images/eqn68.jpg) ) according to the updated HP definition with a witness that extends
) according to the updated HP definition with a witness that extends ![[image]](images/eqn229.jpg) .
.
(b)M′ is a conservative extension of M.
(c)If X = x is a cause of Y = y in (M′, ![[image]](images/eqn68.jpg) ) according to the updated (resp., original) HP definition with a witness extending
) according to the updated (resp., original) HP definition with a witness extending ![[image]](images/eqn232.jpg) then X = x is a cause of Y = y in
then X = x is a cause of Y = y in ![[image]](images/dclimg0111.jpg) according to the updated (resp., original) HP definition with witness
according to the updated (resp., original) HP definition with witness ![[image]](images/eqn234.jpg) .
.
Proof: For part (a), suppose, by way of contradiction, that X = x is a cause of Y = y in (M′, ![[image]](images/eqn68.jpg) ) according to the updated HP definition with a witness
) according to the updated HP definition with a witness ![[image]](images/eqn237.jpg) that extends
that extends ![[image]](images/eqn239.jpg) . If NW ∉
. If NW ∉ ![[image]](images/eqn241.jpg) , then
, then ![[image]](images/eqn242.jpg) . But then, since
. But then, since ![[image]](images/eqn243.jpg) and
and ![[image]](images/eqn244.jpg) , it follows that
, it follows that![[image]](images/eqn246.jpg) , so AC2(bo) fails, contradicting the assumption that X = x is a cause of Y = y in (M′,
, so AC2(bo) fails, contradicting the assumption that X = x is a cause of Y = y in (M′, ![[image]](images/eqn68.jpg) ) according to the original HP definition. Now suppose that NW ∈
) according to the original HP definition. Now suppose that NW ∈ ![[image]](images/eqn248.jpg) . There are two cases, depending on how the value of NW is set in
. There are two cases, depending on how the value of NW is set in ![[image]](images/eqn249.jpg) . If NW = 0, since
. If NW = 0, since ![[image]](images/eqn250.jpg) , AC2(bo) fails; and if NW = 1, since
, AC2(bo) fails; and if NW = 1, since ![[image]](images/eqn251.jpg) , AC2(a) fails. So, in all cases, we get a contradiction to the assumption that X = x is a cause of Y = y in (M′,
, AC2(a) fails. So, in all cases, we get a contradiction to the assumption that X = x is a cause of Y = y in (M′, ![[image]](images/eqn68.jpg) ) according to the original HP definition with a witness
) according to the original HP definition with a witness ![[image]](images/eqn253.jpg) that extends
that extends ![[image]](images/eqn255.jpg) .
.
For part (b), note that the only variable in ![[image]](images/eqn46.jpg) for which the equations in M and M′ are different is Y. Consider any setting of the variables in
for which the equations in M and M′ are different is Y. Consider any setting of the variables in ![[image]](images/eqn46.jpg) other than Y. Except for the two special cases noted above, the value of Y is clearly the same in M and M′. But for these two special cases, as was noted above, the value of NW is “abnormal”, that is, it is not the same as its value according to the equations given the setting of the other variables. It follows that for all settings
other than Y. Except for the two special cases noted above, the value of Y is clearly the same in M and M′. But for these two special cases, as was noted above, the value of NW is “abnormal”, that is, it is not the same as its value according to the equations given the setting of the other variables. It follows that for all settings ![[image]](images/eqn259.jpg) of the variables
of the variables ![[image]](images/eqn260.jpg) in other than Y and all values y″ of Y, we have
in other than Y and all values y″ of Y, we have ![[image]](images/eqn261.jpg) iff
iff ![[image]](images/eqn262.jpg) . Thus, M′ is a conservative extension of M.
. Thus, M′ is a conservative extension of M.
For part (c), suppose that X = x is a cause of Y = y in (M′, ![[image]](images/eqnl59.jpg) ) according to the updated (resp., original) HP definition with witness
) according to the updated (resp., original) HP definition with witness ![[image]](images/eqn264.jpg) . Let
. Let ![[image]](images/eqn266.jpg) and
and ![[image]](images/eqn267.jpg) be the restrictions of
be the restrictions of ![[image]](images/eqn268.jpg) and
and ![[image]](images/eqn269.jpg) , respectively, to the variables in
, respectively, to the variables in ![[image]](images/eqn270.jpg) . If NW ∉
. If NW ∉ ![[image]](images/eqn271.jpg) (so that
(so that ![[image]](images/eqn272.jpg) ), then, since M′ is a conservative extension of M, it easily follows that
), then, since M′ is a conservative extension of M, it easily follows that ![[image]](images/eqn273.jpg) is a witness to X = x being a cause of Y = y in
is a witness to X = x being a cause of Y = y in ![[image]](images/dclimg0112.jpg) according to the updated (resp. original) HP definition. If NW
according to the updated (resp. original) HP definition. If NW ![[image]](images/eqn275.jpg) , then it suffices to show that
, then it suffices to show that ![[image]](images/eqn276.jpg) is also a witness to X = x being a cause of Y = y in (M′,
is also a witness to X = x being a cause of Y = y in (M′, ![[image]](images/eqnl59.jpg) ); that is, NW does not play an essential role in the witness. I now do this.
); that is, NW does not play an essential role in the witness. I now do this.
If NW = 0 is a conjunct of ![[image]](images/eqn279.jpg) , since the equations for Y are the same in M and M′ except for two cases, then the only way that NW = 0 can play an essential role in the witness is if setting
, since the equations for Y are the same in M and M′ except for two cases, then the only way that NW = 0 can play an essential role in the witness is if setting ![[image]](images/eqn280.jpg) and X = x results in
and X = x results in ![[image]](images/eqn281.jpg) and
and ![[image]](images/eqn282.jpg) , for all
, for all ![[image]](images/eqn283.jpg) (i.e., we are in the first of the two cases where the value of Y does not agree in
(i.e., we are in the first of the two cases where the value of Y does not agree in ![[image]](images/dclimg0113.jpg) and (M′,
and (M′, ![[image]](images/eqnl59.jpg) )). But then Y = y′, so if this were the case, AC2(bo) (and hence AC2(bu)) would not hold. Similarly, if NW = 1 is a conjunct of
)). But then Y = y′, so if this were the case, AC2(bo) (and hence AC2(bu)) would not hold. Similarly, if NW = 1 is a conjunct of ![[image]](images/eqn285.jpg) , NW plays a role only if x″ = x′ and setting
, NW plays a role only if x″ = x′ and setting ![[image]](images/eqn286.jpg) and X = x′ results in results in
and X = x′ results in results in ![[image]](images/eqn287.jpg) and
and ![[image]](images/eqn288.jpg) for all
for all ![[image]](images/eqn289.jpg) (i.e., we are in the second of the two cases where the value of Y does not agree in
(i.e., we are in the second of the two cases where the value of Y does not agree in ![[image]](images/dclimg0114.jpg) and (M′,
and (M′, ![[image]](images/eqnl59.jpg) )). But then Y = y, so if this were the case, AC2(a) would not hold, and again we would have a contradiction to X = x being a cause of Y = y in (M′,
)). But then Y = y, so if this were the case, AC2(a) would not hold, and again we would have a contradiction to X = x being a cause of Y = y in (M′, ![[image]](images/eqnl59.jpg) ) with witness
) with witness ![[image]](images/eqn292.jpg) . Thus,
. Thus, ![[image]](images/eqn294.jpg) must be a witness to X = x being a cause of Y = y in (M′,
must be a witness to X = x being a cause of Y = y in (M′, ![[image]](images/eqnl59.jpg) ), and hence also in
), and hence also in ![[image]](images/dclimg0115.jpg) . This completes the proof of part (c). ■
. This completes the proof of part (c). ■
Lemma 4.8.1 is not quite enough to complete the proof of Theorem 4.3.1. There may be several witnesses to X = x being a cause of Y = y in ![[image]](images/dclimg0116.jpg) according to the original HP definition. Although we have removed one of the witnesses, some others may remain, so that X = x may still be a cause of Y = y in (M′,
according to the original HP definition. Although we have removed one of the witnesses, some others may remain, so that X = x may still be a cause of Y = y in (M′, ![[image]](images/eqnl59.jpg) ). But by Lemma 4.8.1(c), if there is a witness to X = x being a cause of Y = y in (M′,
). But by Lemma 4.8.1(c), if there is a witness to X = x being a cause of Y = y in (M′, ![[image]](images/eqnl59.jpg) ), it must extend a witness to X = x being a cause of Y = y in
), it must extend a witness to X = x being a cause of Y = y in ![[image]](images/dclimg0117.jpg) . We can repeat the construction of Lemma 4.8.1 to kill this witness as well. Since there are only finitely many witnesses to X = x being a cause of Y = y in
. We can repeat the construction of Lemma 4.8.1 to kill this witness as well. Since there are only finitely many witnesses to X = x being a cause of Y = y in ![[image]](images/dclimg0118.jpg) , after finitely many extensions, we can kill them all. After this is done, we have a causal model M ∗ extending M such that X = x is not a cause of Y = y in (M ∗,
, after finitely many extensions, we can kill them all. After this is done, we have a causal model M ∗ extending M such that X = x is not a cause of Y = y in (M ∗, ![[image]](images/eqn68.jpg) ) according to the original HP definition. ■
) according to the original HP definition. ■
It is interesting to apply the construction of Theorem 4.3.1 to Example 2.8.1 (the loaded-gun example). The variable NW added by the construction is almost identical to the extra variable B′ (where B′ = A ∧ B—B shoots a loaded gun) added in Example 2.8.1 to show that this example could be dealt with using the original HP definition. Indeed, the only difference is that NW = 0 if A = B = C = 1, while B′ = 1 in this case. But since D = 1 if A = B = C = 1 and NW = 0, the equations for D are the same in both causal models if A = B = C = 1. Although it seems strange, given our understanding of the meaning of the variables, to have NW = 0 if A = B = C = 1, it is easy to see that this definition works equally well in showing that A = 1 is not a cause of D = 1 in the context where A = 1, B = 0, and C = 1 according to the original HP definition.
4.8.3 Proofs and example for Section 4.4
I start with the proof of Theorem 4.4.1.
Theorem 4.4.1: For all n ≥ 0, Mn+1 is a conservative extension of Mn. Moreover, B = 1 is not part of a cause of VS = 1 in (M2n, u1), and B = 1 is part of a cause of VS = 1 in (M2n+1, u1), for n = 0, 1, 2, … (according to all variants of the HP definition).
Proof: Fix n ≥ 0. To see that M2n+1 is a conservative extension of M2n, note that, aside from VS, the equations for all endogenous variables that appear in both M2n and M2n+1 (namely, B, VS, A1,…, An, PN 1,…, PN n) are the same in both models. Thus, it clearly suffices to show that, for every setting of the variables U, B, A1,…, An, PN1,…, PNn, the value of VS is the same in both M2n and M2n+1. Clearly, in the context u0, VS = 0 in both models. In the context u1, note that if both Aj and PNj are 0 for some j 1,…, n, then VS = 0 in both M2n and M2n+1. (Again, recall that Aj = 0 means that assassin #j puts poison in the coffee.) If one of Aj and PNj is 1 for all j ∈ {1,…, n}, then VS = 1 in both M2n and M2n+1 (in the latter case because An+1 = 1 in (M2n+1, u1)).
The argument to show that M2n+2 is a conservative extension of M2n+1 is similar in spirit. Now the equations for all variables but VS and PNn+1 are the same in M2n+1 and M2n+2. It clearly suffices to show that, for every setting of the variables U, B, A1,…, An, An+1, PN1,…, PNn, the value of VS is the same in both M2n+1 and M2n+2. Clearly in context u0, VS = 0 in both models. In u1, note that if both Aj and PNj are 0 for some j 1,…, n, then VS = 0 in both M2n+1 and M2n+2. So suppose that one of Aj and PNj is 1 for all j ∈ {1,…, n}. If An+1 = 1, then VS = 1 in both M2n+1 and M2n+2; and if An+1 = 0, then VS = B in both M2n+1 and M2n+2 (in the latter case, because VS = PNn+1, and PNn+1 = B if An+1 = 0).
To see that B = 1 is part of a cause of VS = 1 in (M2n+1, u1) according to all variants of the HP definition, observe that
![[image]](images/eqn300.jpg)
Clearly just setting B to 0 or An+1 to 0 is not enough to make VS = 0, no matter which other variables are held at their actual values. Thus, B = 1 ∧ An+1 = 1 is a cause of VS = 1 in (M2n+1, u1) according to the modified HP definition. It follows from Theorem 2.2.3 that B = 1 is a cause of VS = 1 in (M2n+1, u1) according to the original and updated definition as well.
Finally, to see that, according to all the variants of the HP definition, B = 1 is not part of a cause of VS = 1 in (M2n+2, u1), first suppose, by way of contradiction, that it is a cause according to the original HP definition, with witness ![[image]](images/eqn301.jpg) . By AC2(a), we must have
. By AC2(a), we must have ![[image]](images/eqn303.jpg) . Thus, it must be the case that either (1) there is some j ≤ n + 1 such that Aj, PNj ∈
. Thus, it must be the case that either (1) there is some j ≤ n + 1 such that Aj, PNj ∈ ![[image]](images/eqn304.jpg) and in
and in ![[image]](images/eqn305.jpg) , both Aj and PNj are set to 0; or (2) for some j ≤ n + 1, Aj ∈
, both Aj and PNj are set to 0; or (2) for some j ≤ n + 1, Aj ∈ ![[image]](images/eqn306.jpg) , PNj ∈
, PNj ∈ ![[image]](images/eqn307.jpg) , and Aj is set to 0 in
, and Aj is set to 0 in ![[image]](images/eqn308.jpg) . In case (1), we must have
. In case (1), we must have ![[image]](images/eqn309.jpg) , so AC2(bo) does not hold. In case (2), since
, so AC2(bo) does not hold. In case (2), since ![[image]](images/eqn310.jpg) in the actual world, and
in the actual world, and ![[image]](images/eqn311.jpg) (since Aj is set to 0 when
(since Aj is set to 0 when ![[image]](images/eqn312.jpg) is set to
is set to ![[image]](images/eqn313.jpg) ), AC2(bo) again does not hold. Thus, B = 1 is not a cause of VS = 1 in (M2n+2, u1) according to the original HP definition. (Not surprisingly, this is just a generalization of the argument used in Section 3.4.1.) By Theorem 2.2.3, it follows that B = 1 is not part of a cause of VS = 1 in (M2n+2, u1) according to the updated or modified HP definition either. ■
), AC2(bo) again does not hold. Thus, B = 1 is not a cause of VS = 1 in (M2n+2, u1) according to the original HP definition. (Not surprisingly, this is just a generalization of the argument used in Section 3.4.1.) By Theorem 2.2.3, it follows that B = 1 is not part of a cause of VS = 1 in (M2n+2, u1) according to the updated or modified HP definition either. ■
I next prove Theorem 4.4.4.
Theorem 4.4.4: Suppose that M and M′ are extended causal models such that M′ is a conservative extension of M, the normality ordering in M′ respects the equations for all variables in ![[image]](images/eqn314.jpg) relative to
relative to ![[image]](images/eqnl59.jpg) , where
, where ![[image]](images/eqn315.jpg) and
and ![[image]](images/eqn316.jpg) are the sets of endogenous variables in M and M′, respectively, and all the variables in φ are in
are the sets of endogenous variables in M and M′, respectively, and all the variables in φ are in ![[image]](images/eqn318.jpg) . Then the following holds:
. Then the following holds:
(a)According to the original and updated HP definition, if ![[image]](images/eqn319.jpg) is not a cause of φ in
is not a cause of φ in ![[image]](images/dclimg0119.jpg) , then either
, then either ![[image]](images/eqn320.jpg) is not a cause of φ in (M′,
is not a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ) or there is a strict subset
) or there is a strict subset ![[image]](images/eqn322.jpg) of
of ![[image]](images/eqn323.jpg) such that
such that ![[image]](images/eqn324.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dclimg0120.jpg) , where
, where ![[image]](images/eqn325.jpg) is the restriction of
is the restriction of ![[image]](images/eqn326.jpg) to the variables in
to the variables in ![[image]](images/eqn327.jpg) .
.
(b)According to the modified HP definition, ![[image]](images/eqn328.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/eqn329.jpg) is a cause of φ in (M′,
is a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ) (so, in particular, a cause of φ in (M′,
) (so, in particular, a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ) cannot involve a variable in
) cannot involve a variable in ![[image]](images/eqn60.jpg) ).
).
Proof: I first prove part (a) for the updated definition. Suppose that ![[image]](images/eqn333.jpg) is not a cause of φ in
is not a cause of φ in ![[image]](images/dclimg0122.jpg) according to the updated HP definition, but is a cause of φ in (M′,
according to the updated HP definition, but is a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ), with witness
), with witness ![[image]](images/eqn335.jpg) . Let
. Let ![[image]](images/eqn338.jpg) be the intersection of
be the intersection of ![[image]](images/eqn339.jpg) with
with ![[image]](images/eqn340.jpg) , the set of endogenous variables in M, let
, the set of endogenous variables in M, let ![[image]](images/eqn341.jpg) , and let
, and let ![[image]](images/eqn342.jpg) be the restriction of
be the restriction of ![[image]](images/eqn343.jpg) to the variables in
to the variables in ![[image]](images/eqn344.jpg) . Since
. Since ![[image]](images/eqn345.jpg) is not a cause of φ in
is not a cause of φ in ![[image]](images/dclimg0123.jpg) , it is certainly not a cause with witness
, it is certainly not a cause with witness ![[image]](images/eqn346.jpg) , so either (i)
, so either (i) ![[image]](images/eqn349.jpg) (i.e., AC1 is violated); (ii)
(i.e., AC1 is violated); (ii) ![[image]](images/eqn350.jpg) or
or ![[image]](images/eqn351.jpg) (i.e., AC2+(a) is violated); (iii) there exist subsets
(i.e., AC2+(a) is violated); (iii) there exist subsets ![[image]](images/eqn352.jpg) of
of ![[image]](images/eqn353.jpg) and
and ![[image]](images/eqn354.jpg) of
of ![[image]](images/eqn355.jpg) such that if
such that if ![[image]](images/eqn356.jpg) (i.e.,
(i.e., ![[image]](images/eqn357.jpg) gives the actual values of the variables in
gives the actual values of the variables in ![[image]](images/eqn358.jpg) ), then
), then ![[image]](images/eqn359.jpg) (i.e., AC2(bu) is violated); or (iv) there is a strict subset
(i.e., AC2(bu) is violated); or (iv) there is a strict subset ![[image]](images/eqn360.jpg) of
of ![[image]](images/eqn361.jpg) such that
such that ![[image]](images/eqn362.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dclimg0124.jpg) , where
, where ![[image]](images/eqn363.jpg) is the restriction of
is the restriction of ![[image]](images/eqn364.jpg) to the variables in
to the variables in ![[image]](images/eqn365.jpg) (i.e., AC3 is violated). Since M′ is a conservative extension of M, by Lemma 4.2.2, if (i) or (iii) holds, then the same statement holds with M replaced by M′, showing that
(i.e., AC3 is violated). Since M′ is a conservative extension of M, by Lemma 4.2.2, if (i) or (iii) holds, then the same statement holds with M replaced by M′, showing that ![[image]](images/eqn366.jpg) is not a cause of φ in (M′,
is not a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ) with witness
) with witness ![[image]](images/eqn368.jpg) .
.
Now suppose that (ii) holds. For each variable ![[image]](images/eqn371.jpg) , let v be the value of V in
, let v be the value of V in ![[image]](images/eqn372.jpg) . Further assume that for all
. Further assume that for all ![[image]](images/eqn373.jpg) , we have
, we have ![[image]](images/eqn374.jpg) . I show that this additional assumption leads to a contradiction. With this additional assumption, if
. I show that this additional assumption leads to a contradiction. With this additional assumption, if ![[image]](images/eqn375.jpg) , then
, then ![[image]](images/eqn376.jpg) , so if the reason that
, so if the reason that ![[image]](images/eqn377.jpg) is not a cause of φ in
is not a cause of φ in ![[image]](images/dclimg0125.jpg) is that AC2(a) is violated, then AC2(a) is also violated in (M′,
is that AC2(a) is violated, then AC2(a) is also violated in (M′, ![[image]](images/eqnl59.jpg) ), and
), and ![[image]](images/eqn379.jpg) is not a cause of φ in (M′,
is not a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ) with witness
) with witness ![[image]](images/eqn381.jpg) , a contradiction. Moreover, it follows that
, a contradiction. Moreover, it follows that ![[image]](images/eqn384.jpg) . By CE in the definition of conservative extension, if
. By CE in the definition of conservative extension, if ![[image]](images/eqn385.jpg) , and hence
, and hence ![[image]](images/eqn386.jpg) . So if the reason that
. So if the reason that ![[image]](images/eqn387.jpg) is not a cause of φ in
is not a cause of φ in ![[image]](images/dclimg0126.jpg) is that the normality condition in AC2+(a) is violated, it is also violated in (M′,
is that the normality condition in AC2+(a) is violated, it is also violated in (M′, ![[image]](images/eqnl59.jpg) ), and again we get a contradiction.
), and again we get a contradiction.
Thus, we must have ![[image]](images/eqn389.jpg) for some variable
for some variable ![[image]](images/eqn390.jpg) . That means that the variable V takes on a value other than that specified by the equations in (M′,
. That means that the variable V takes on a value other than that specified by the equations in (M′, ![[image]](images/eqnl59.jpg) ). Since, by assumption, M′ respects the equations for V relative to --u, we have
). Since, by assumption, M′ respects the equations for V relative to --u, we have ![[image]](images/eqn392.jpg) , contradicting the assumption that
, contradicting the assumption that ![[image]](images/eqn393.jpg) is a cause of φ in (M′,
is a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ) with witness
) with witness ![[image]](images/eqn395.jpg) . Either way, if (ii) holds, we get a contradiction. I leave it to the reader to check that the same contradiction can be obtained using the alternative version of AC2+(a) where normality is defined on contexts (and similarly for the remaining arguments in the proof of this result).
. Either way, if (ii) holds, we get a contradiction. I leave it to the reader to check that the same contradiction can be obtained using the alternative version of AC2+(a) where normality is defined on contexts (and similarly for the remaining arguments in the proof of this result).
Thus, either ![[image]](images/eqn398.jpg) is not a cause of φ in (M′,
is not a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ) or
) or ![[image]](images/eqn400.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dclimg0127.jpg) for some strict subset
for some strict subset ![[image]](images/eqn401.jpg) .
.
I leave it to the reader to check that the same argument goes through with essentially no change in the case of the original HP definition. For future reference, note that it also goes through with minimal change for the modified HP definition; we simply use AC2(am) rather than AC2(a) and drop case (iii).
For part (b), first suppose by way of contradiction that, according to the modified HP definition, ![[image]](images/eqn402.jpg) is not a cause of φ in (M′,
is not a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ) but is a cause of φ in
) but is a cause of φ in ![[image]](images/dclimg0128.jpg) with witness
with witness ![[image]](images/eqn404.jpg) . Since M′ is a conservative extension of M, AC2+(am) must hold for
. Since M′ is a conservative extension of M, AC2+(am) must hold for ![[image]](images/eqn407.jpg) with witness
with witness ![[image]](images/eqn408.jpg) . (Here again, I am using condition CE to argue that
. (Here again, I am using condition CE to argue that ![[image]](images/eqn411.jpg) is more normal than
is more normal than ![[image]](images/eqn412.jpg) in M′ because this is the case in M.) Thus, if
in M′ because this is the case in M.) Thus, if ![[image]](images/eqn413.jpg) is not a cause of φ in M′, AC3 must fail, and there must be a strict subset
is not a cause of φ in M′, AC3 must fail, and there must be a strict subset ![[image]](images/eqn414.jpg) of
of ![[image]](images/eqn415.jpg) such that
such that ![[image]](images/eqn416.jpg) is a cause of φ in (M′,
is a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ), where
), where ![[image]](images/eqn418.jpg) is the restriction of
is the restriction of ![[image]](images/eqn419.jpg) to
to ![[image]](images/eqn420.jpg) . Clearly
. Clearly ![[image]](images/eqn421.jpg) is not a cause of φ in
is not a cause of φ in ![[image]](images/dclimg0129.jpg) , for otherwise
, for otherwise ![[image]](images/eqn422.jpg) would not be a cause of φ in
would not be a cause of φ in ![[image]](images/dclimg0130.jpg) . Thus, as observed in the proof of part (a), since
. Thus, as observed in the proof of part (a), since ![[image]](images/eqn423.jpg) is a cause of φ in (M′,
is a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ) according to the modified HP definition, there must be a strict subset
) according to the modified HP definition, there must be a strict subset ![[image]](images/eqn425.jpg) of
of ![[image]](images/eqn426.jpg) such that
such that ![[image]](images/eqn427.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dclimg0131.jpg) according to the modified HP definition, where
according to the modified HP definition, where ![[image]](images/eqn428.jpg) is the restriction of
is the restriction of ![[image]](images/eqn429.jpg) to
to ![[image]](images/eqn430.jpg) . But this contradicts the assumption that
. But this contradicts the assumption that ![[image]](images/eqn431.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dclimg0132.jpg) , since then AC3 does not hold.
, since then AC3 does not hold.
For the converse, suppose that ![[image]](images/eqn432.jpg) is a cause of φ in (M′,
is a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ) with witness
) with witness ![[image]](images/eqn434.jpg) . Thus
. Thus ![[image]](images/eqn437.jpg) . Let
. Let ![[image]](images/eqn438.jpg) , let
, let ![[image]](images/eqn439.jpg) , let
, let ![[image]](images/eqn440.jpg) , let
, let ![[image]](images/eqn441.jpg) , and let
, and let ![[image]](images/eqn442.jpg) and
and ![[image]](images/eqn443.jpg) be the restrictions of
be the restrictions of ![[image]](images/eqn444.jpg) and
and ![[image]](images/eqn445.jpg) to the variables in
to the variables in ![[image]](images/eqn446.jpg) and
and ![[image]](images/eqn447.jpg) , respectively, for i = 1, 2. Since the normality ordering in M′ respects the equations for all the variables in
, respectively, for i = 1, 2. Since the normality ordering in M′ respects the equations for all the variables in ![[image]](images/eqn448.jpg) relative to
relative to ![[image]](images/eqn449.jpg) , it is not hard to show that
, it is not hard to show that ![[image]](images/eqn450.jpg) . For otherwise,
. For otherwise, ![[image]](images/eqn451.jpg) , and AC2+(am) would not hold, contradicting the assumption that
, and AC2+(am) would not hold, contradicting the assumption that ![[image]](images/eqn452.jpg) is a cause of φ in (M′,
is a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ) with witness
) with witness ![[image]](images/eqn454.jpg) . Since
. Since ![[image]](images/eqn457.jpg) , it follows by Lemma 2.10.2 that
, it follows by Lemma 2.10.2 that ![[image]](images/eqn458.jpg) . Since we are dealing with the modified HP definition,
. Since we are dealing with the modified HP definition, ![[image]](images/eqn459.jpg) , so
, so ![[image]](images/eqn460.jpg) must be nonempty. We must have
must be nonempty. We must have ![[image]](images/eqn461.jpg) , otherwise
, otherwise ![[image]](images/eqn462.jpg) cannot be a cause of φ in (M′,
cannot be a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ); we would have a violation of AC3. I claim that
); we would have a violation of AC3. I claim that ![[image]](images/eqn464.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dclimg0133.jpg) , as desired. For if not, we can apply the same argument as in part (a) (which, as I observed above, also holds for the modified HP definition) to show that there must be a strict subset
, as desired. For if not, we can apply the same argument as in part (a) (which, as I observed above, also holds for the modified HP definition) to show that there must be a strict subset ![[image]](images/eqn465.jpg) of
of ![[image]](images/eqn466.jpg) such that
such that ![[image]](images/eqn467.jpg) is a cause of φ in (M′,
is a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ), where
), where ![[image]](images/eqn469.jpg) is the restriction of
is the restriction of ![[image]](images/eqn470.jpg) to
to ![[image]](images/eqn471.jpg) . But this contradicts the assumption that
. But this contradicts the assumption that ![[image]](images/eqn472.jpg) is a cause of φ in (M′,
is a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ). ■
). ■
Theorem 4.4.5: According to the original and updated HP definition, if (a) M′ is a conservative extension of M, (b) M″ is a conservative extension of M′, (c) ![[image]](images/eqn474.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dclimg0134.jpg) and (M″,
and (M″, ![[image]](images/eqn68.jpg) ), (d) the normality ordering in M′ respects the equations for all endogenous variables in M′ not in M relative to
), (d) the normality ordering in M′ respects the equations for all endogenous variables in M′ not in M relative to ![[image]](images/eqn68.jpg) , and (e) the normality ordering in M″ respects the equations for all endogenous variables in M″ not in M′ relative to
, and (e) the normality ordering in M″ respects the equations for all endogenous variables in M″ not in M′ relative to ![[image]](images/eqn477.jpg) , then
, then ![[image]](images/eqn478.jpg) is also a cause of φ in (M′,
is also a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ).
).
Proof: The same argument work for both the original and updated HP definition. Suppose by way of contradiction that ![[image]](images/eqn480.jpg) is not a cause of φ in (M′,
is not a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ). By Theorem 4.4.1(a), there must be a strict subset
). By Theorem 4.4.1(a), there must be a strict subset ![[image]](images/eqn482.jpg) of
of ![[image]](images/eqn483.jpg) such that
such that ![[image]](images/eqn484.jpg) is a cause of φ in (M′,
is a cause of φ in (M′, ![[image]](images/eqnl59.jpg) ), where
), where ![[image]](images/eqn486.jpg) is the restriction of
is the restriction of ![[image]](images/eqn487.jpg) to the variables in
to the variables in ![[image]](images/eqn488.jpg) . But
. But ![[image]](images/eqn489.jpg) cannot be a cause of φ in
cannot be a cause of φ in ![[image]](images/dclimg0135.jpg) , for then, by AC3,
, for then, by AC3, ![[image]](images/eqn490.jpg) would not be a cause of φ in
would not be a cause of φ in ![[image]](images/dclimg0136.jpg) . By Theorem 4.4.1(a) again, there must be a strict subset
. By Theorem 4.4.1(a) again, there must be a strict subset ![[image]](images/eqn491.jpg) of
of ![[image]](images/eqn492.jpg) such that
such that ![[image]](images/eqn493.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dclimg0137.jpg) , where
, where ![[image]](images/eqn494.jpg) is the restriction of
is the restriction of ![[image]](images/eqn495.jpg) to
to ![[image]](images/eqn496.jpg) . But then, by AC3,
. But then, by AC3, ![[image]](images/eqn497.jpg) cannot be a cause of φ in
cannot be a cause of φ in ![[image]](images/dclimg0138.jpg) , giving us the desired contradiction. ■
, giving us the desired contradiction. ■
I next give an example showing that it is possible for ![[image]](images/eqn498.jpg) to go from being a non-cause of φ to being a cause to being a non-cause again according to the updated HP definition, even taking normality into account, showing that Theorem 4.4.5 is the best we can do. Because this type of behavior can happen only if causes are not single conjuncts, it is perhaps not so surprising that the example is a variant of Example 2.8.2, which shows that according to the updated HP definition, a cause may involve more than one conjunct.
to go from being a non-cause of φ to being a cause to being a non-cause again according to the updated HP definition, even taking normality into account, showing that Theorem 4.4.5 is the best we can do. Because this type of behavior can happen only if causes are not single conjuncts, it is perhaps not so surprising that the example is a variant of Example 2.8.2, which shows that according to the updated HP definition, a cause may involve more than one conjunct.
Example 4.8.2 I start with a simplified version of the model in Example 2.8.2, where there is no variable D′. Again, A votes for a candidate. A’s vote is recorded in two optical scanners B and C. D collects the output of the scanners. The candidate wins (i.e., WIN = 1) if any of A, B, or D is 1. The value of A is determined by the exogenous variable. The following structural equations characterize the remaining variables:
Call the resulting causal model M. In the actual context u, A = 1, so B = C = D = WIN = 1. Assume that all worlds in M are equally normal.
I claim that B = 1 is a cause of WIN = 1 in (M, u) according to the updated HP definition. To see this, take ![[image]](images/eqn499.jpg) . Consider the contingency where A = 0. Clearly if B = 0, then WIN = 0, and if B = 1, then WIN = 1. It is easy to check that AC2 holds. Moreover, since B = 1 is a cause of WIN = 1 in (M, u), by AC3, B = 1 ∧ C = 1 cannot be a cause of WIN = 1 in (M, u).
. Consider the contingency where A = 0. Clearly if B = 0, then WIN = 0, and if B = 1, then WIN = 1. It is easy to check that AC2 holds. Moreover, since B = 1 is a cause of WIN = 1 in (M, u), by AC3, B = 1 ∧ C = 1 cannot be a cause of WIN = 1 in (M, u).
Now consider the model M′ from Example 2.8.2. Recall that it is just like M, except that there is one more exogenous variable D′, where D′ = B ∧ ¬ A. The equation for WIN now becomes WIN = A ∨ D′ ∨ D. All the other equations in M′ are the same as those in M. Define the normality ordering in M′ so that it respects the equations for D′ relative to u: all worlds where D′ = B ∧ ¬A are equally normal; all worlds where D′ ≠ B ∧ ¬A are also equally normal, but less normal than worlds where D′ = B ∧ ¬A.
It is easy to see that M′ is a conservative extension of M. Since D′ does not affect any variable but WIN, and all the equations except that for WIN are unchanged, it suffices to show that for all settings of the variables other than D′ and WIN, WIN has the same value in context u in both M and M′. Clearly if A = 1 or D = 1, then WIN = 1 in both M and M′. So suppose that we set A = D = 0. Now if B = 1, then D′ = 1 (since A = 0), so again WIN = 1 in both M and M′. In contrast, if B = 0, then D′ = 0, so WIN = 0 in both M and M′. Condition CE clearly holds as well. As shown in Example 2.8.2, B = 1 ∧ C = 1 is a cause of WIN = 1 in (M′, u).
Finally, consider the model M″ that is just like M′ except that it has one additional variable D″, where D″ = D ∧ ¬ A and the equation for WIN becomes WIN = A ∨ D′ ∨ D″. All the other equations in M″ are the same as those in M′. Define the normality ordering in M′ so that it respects the equations for both D′ and D″ relative to u.
It is easy to check that M″ is a conservative extension of M′. Since D″ does not affect any variable but WIN, and all the equations except that for WIN are unchanged, it suffices to show that for all settings of the variables other than D″ and WIN, WIN has the same value in context u in both M and M′. Clearly if A = 1 or D′ = 1, then WIN = 1 in both M′ and M″. And if A = D = 0, then D′ = 1 iff D = 1, so again the value of WIN is the same in M′ and M″. Condition CE clearly holds as well.
Finally, I claim that B = 1 ∧ C = 1 is no longer a cause of WIN = 1 in (M″, u) according to the updated HP definition. Suppose, by way of contradiction, that it is, with witness ![[image]](images/eqn500.jpg) . A = 0 must be a conjunct of
. A = 0 must be a conjunct of ![[image]](images/eqn503.jpg) . It is easy to see that either D′ = 0 is a conjunct of
. It is easy to see that either D′ = 0 is a conjunct of ![[image]](images/eqn504.jpg) or D′ ∉
or D′ ∉ ![[image]](images/eqn505.jpg) , and similarly for D″. Since D′ = D″ = 0 in the context u and
, and similarly for D″. Since D′ = D″ = 0 in the context u and ![[image]](images/eqn506.jpg) , it easily follows that AC2(bu) does not hold, regardless of whether D′ and D″ are in
, it easily follows that AC2(bu) does not hold, regardless of whether D′ and D″ are in ![[image]](images/eqn507.jpg) .
.
Thus, B = 1 ∧ C = 1 goes from not being a cause of WIN = 1 in (M, u) to being a cause of WIN = 1 in (M′, u) to not being a cause of of WIN = 1 in (M″, u). ■
Paul and Hall [2013], among many others, seem to take it for granted that causality should be objective, but they do express sympathy for what they call a “mixed approach” that “would be sensitive to the need to give a suitably objective account of the causal structure of the world, yet recognize that any account that can do justice to our causal intuitions will have to have some pragmatic features … ” [Paul and Hall 2013, p. 254]. Arguably, the HP approach is such a mixed approach.
Most of the discussion in Sections 4.1–4.4 is taken from [Halpern 2014a]. The example regarding different causes of a traffic accident is a variant of an example originally due to Hanson [1958].
Issues of stability have been considered before. Strevens [2008] provides an example where what Strevens calls a cause can become a non-cause if extra variables are added according to Woodward’s [2003] definition of causality (actually, Strevens considered what Woodward called a contributing cause); Eberhardt [2014] shows that this can also happen for type causality using Woodward’s definition. However, [Halpern 2014a] seems to have been the first systematic investigation of stability. Huber [2013] defines causality using a ranking function on worlds and proposes a condition similar in spirit to that of a normality ordering respecting the equations (although he does not apply it in the context of stability).
Example 4.1.1 is due to Spohn [personal communication, 2012]. Example 4.1.2 is due to Weslake [2015]. Example 4.1.3 is a slight simplification of an example due to Hall [2007]. (Hall [2007] also has variables C and F such that C = B and F = E; adding them does not affect any of the discussion here (or in Hall’s paper).) Of the conclusion that D = 1 is a cause of E = 1 in (M′, u), Hall [2007] says, “This result is plainly silly, and doesn’t look any less silly if you insist that causal claims must always be relativized to a model.” I disagree. To be more precise, I would argue that Hall has in mind a particular picture of the world: that captured by model M. Of course, if that is the “right” picture of the world, then the conclusion that D = 1 is a cause of B = 1 is indeed plainly silly. But for the story with Xavier, it does not seem (to me) at all unreasonable that D = 1 should be a cause of B = 1.
Example 4.1.4 is due to Glymour et al. [2010]; Example 4.1.5 is taken from [Halpern 2015a]. Example 4.6.1 is a simplification of an example introduced by Bennett [1987]. Hitchcock [2012] has an extended discussion of Example 4.6.1.
Most of the discussion in Sections 4.5–4.7 is taken from [Halpern and Hitchcock 2010]. In particular, the question of how the variables and the ranges of variables in a causal model should be chosen is discussed there. Woodward [2016] picks up on the theme of variable choice and provides some candidate criteria, such as choosing variables that are well-defined targets for interventions and choosing variables that can be manipulated to any of their possible values independently of the values taken by other variables.
The issue of the set of possible values of a variable is related to discussions about the metaphysics of “events”. (Note that usage of the word “event” in the philosophy literature is different from the typical usage of the word in computer science and probability, where an event is just a subset of the state space. See the notes at the end of Chapter 2 for more discussion.) Suppose that the homeowner in Section 4.5 pushed on the door with enough force to open it. Some philosophers, such as Davidson [1967], have argued that this should be viewed as just one event, the push, that can be described at various levels of detail, such as a “push” or a “hard push”. Others, such as Kim [1973] and Lewis [1986c], have argued that there are many different events corresponding to these different descriptions. If we take the latter view, which of the many events that occur should be counted as causes of the door’s opening? In the HP definition, these questions must all be dealt with at the time that the variables describing a model and their ranges are chosen. The question then becomes “what choice of variables describes the effects of interventions in a way that is not misleading or ambiguous”. Of course, whether a particular description does so is a matter that can be argued (by lawyers, among others).
The fact that someone is not held liable for damages if he acts as the hypothetical “reasonable person” would have done in similar circumstances is discussed by Hart and Honoré [1985, pp. 142ff.]. They also discuss circumstances under which malicious acts of third parties are considered to be “abnormal” interventions and affect the assessment of causation (see [Hart and Honoré 1985, pp. 68]).
Complexity and Axiomatization
The complexities of cause and effect defy analysis.
Douglas Adams, Dirk Gently’s Holistic Detective Agency
Is it plausible that people actually work with structural equations and (extended) causal models to evaluate actual causation? People are cognitively limited. If we represent the structural equations and the normality ordering in what is perhaps the most obvious way, the models quickly become large and complicated, even with a small number of variables.
To understand the problem, consider a doctor trying to deal with a patient who has just come in reporting bad headaches. Let’s keep things simple. Suppose that the doctor considers only a small number of variables that might be relevant: stress, constriction of blood vessels in the brain, aspirin consumption, and trauma to the head. Again, keeping things simple, assume that each of these variables (including headaches) is binary; that is, has only two possible values. So, for example, the patient either has a headache or not. Each variable may depend on the value of the other four. To represent the structural equation for the variable “headaches”, a causal model will need to assign a value to “headaches” for each of the sixteen possible values of the other four variables. That means that there are 216—over 60,000!— possible equations for “headaches”. Considering all five variables, there are 280 (over 1024) possible sets of equations. Now consider the normality ordering. With five binary variables, there are 25 = 32 possible assignments of values to these variables. Think of each of these assignments as a “possible world”. There are 32! (roughly 2.6 × 1035) strict orders of these 32 worlds, and many more if we allow for ties or incomparable worlds. Altogether, the doctor would need to store close to two hundred bits of information just to represent this simple extended causal model.
Now suppose we consider a more realistic model with 50 random variables. Then the same arguments show that we would need as many as ![[image]](images/eqn508.jpg) possible sets of equations, 250 possible worlds, and over
possible sets of equations, 250 possible worlds, and over ![[image]](images/eqn509.jpg) normality orderings (in general, with n binary variables, there are
normality orderings (in general, with n binary variables, there are ![[image]](images/eqn510.jpg) sets of equations, 2n possible worlds, and
sets of equations, 2n possible worlds, and ![[image]](images/eqn511.jpg) strict orders). Thus, with 50 variables, roughly 50 × 250 bits would be needed to representing a causal model. This is clearly cognitively unrealistic.
strict orders). Thus, with 50 variables, roughly 50 × 250 bits would be needed to representing a causal model. This is clearly cognitively unrealistic.
If the account of actual causation given in the preceding chapters is to be at all realistic as a model of human causal judgment, some form of compact representation will be needed. Fortunately, as I show in this chapter, in practice, things are likely to be much better; it is quite reasonable to expect that most “natural” models can be represented compactly. At a minimum, we cannot use these concerns about compact representations to argue that people cannot be using (something like) causal models to reason about causality.
But even given a compact representation, how hard is it to actually compute whether X = x is a cause of Y = y? It is not hard to exhaustively check all the possibilities if there are relatively few variables involved or in structures with a great deal of symmetry. This has been the case for all the examples I have considered thus far. But, as we shall see in Chapter 8, actual causality can also be of great use in, for example, reasoning about the correctness of programs and in answering database queries. Large programs and databases may well have many variables, so now the question of the complexity of determining actual causality becomes a significant issue. Computer science provides tools to formally characterize the complexity of determining actual causation; I discuss these in Section 5.3.
In many cases, we do not have a completely specified causal model. Rather, what we know are certain facts about the model: for example, we might know that, although X is actually 1, if X were 0, then Y would be 0. The question is what conclusions about causality we can draw from such information. In Section 5.4, I discuss axioms for causal reasoning.
Note to the reader: the four sections in this chapter can be read independently. The material in this chapter is more technical than that of the other chapters in this book; I have deferred the most technical to Section 5.5. The rest of the material should be accessible even to readers with relatively little mathematical background.
5.1 Compact Representations of Structural Equations
The calculations above on the complexity of representing structural equations just gave naive upper bounds. Suppose that whether the patient has a headache is represented by the variable H, and the patient has a headache iff any of the conditions X1,…, Xk holds. Rather than painfully writing out the 2k possible settings of the variables X1,…, Xk and the corresponding setting of H, we can simply write one line: H = X1 ∨… ∨ Xk. Indeed, as long as all variables are binary, we can always describe the effect of X1,…, Xk on H by a single propositional formula. However, in general, this formula will have a length that is exponential in k; we cannot count on it having a short description as in this example. So, in the worst case, we have either 2k short equations or one long equation. Can anything be done to mitigate this?
The first step toward the goal of getting a compact representation comes from the observation that similar representational difficulties arise when it comes to reasoning about probability. For example, if a doctor would like to reason probabilistically about a situation where there are 50 binary variables describing symptoms and potential diseases that a patient might have, just describing a probability distribution on the 250 possible worlds would also require 250 (more precisely, 250 − 1) numbers. Bayesian networks have been used to provide compact representations of probability distributions; they exploit (conditional) independencies between variables. As I mentioned in the notes to Chapter 2, the causal networks that we have been using to describe causal models are similar in spirit to Bayesian networks. This similarity is quite suggestive; the same ideas that allow Bayesian networks to provide compact representations of probability distributions can be applied in the setting of causal models.
Although a thorough discussion of Bayesian networks is well beyond the scope of this book, it is easy to see where independence comes in, both in the probabilistic setting and in the setting of causality. If X1,…, Xn are independent binary variables, then we can represent a probability distribution on the 2n possible worlds generated by these variables using only n numbers rather than 2n numbers. Specifically, the values Pr(Xi = 0), i = 1,…, n, completely determine the distribution. From them, we can compute Pr(Xi = 1) for i = 1,…, n. The probability Pr(X1 = i1 ∧ … Xn = in) for ∈ ij {0, 1}, j = 1,…, n, is then determined, thanks to the assumption that X1,…, Xn are independent.
Of course, it is rarely the case that we are considering a situation described by n variables that are all independent of each other. Most situations of interest involve variables that are somehow related to each other. However, it is still the case that there are often some variables that are (conditionally) independent of others. It turns out that if no variable depends on too many other variables, then we can get a significantly more compact representation of the distribution. Similarly, if the structural equations are such that each variable depends on the values of only a few other variables, then we can again get a significantly simpler representation of the equations.
Consider the model ![[image]](images/eqn512.jpg) for the rock-throwing example again. The variable BS is affected by BT; if ST = 0 (Suzy doesn’t throw), then BS = BT. However, the effect of BT on BS is mediated by BH. Once we know the value of BH, the value of BS is irrelevant. We can think of BS as being independent of BT, conditional on BH. Similarly, BS is independent of ST given SH. So, although BS is affected by all of ST, BT, BH, and SH, its value is completely determined by SH and BH. This is made clear by the equation that we used for BS: BS = SH ∨ BH.
for the rock-throwing example again. The variable BS is affected by BT; if ST = 0 (Suzy doesn’t throw), then BS = BT. However, the effect of BT on BS is mediated by BH. Once we know the value of BH, the value of BS is irrelevant. We can think of BS as being independent of BT, conditional on BH. Similarly, BS is independent of ST given SH. So, although BS is affected by all of ST, BT, BH, and SH, its value is completely determined by SH and BH. This is made clear by the equation that we used for BS: BS = SH ∨ BH.
A causal network describes these conditional independencies. The key point is that the value of a variable in the graph is completely determined by the values of its parents in the graph. As long as each variable has at most k parents in the graph, we can describe the structural equations using 2kn equations in the worst case, rather than 2n−1n equations. (Needless to say, the connection to Bayesian networks is not purely coincidental!) Again, if all variables are binary, we can effectively combine the 2kn or 2n−1n into one formula, but in the worst case, the length of the formula will be comparable to the total length of the short equations corresponding to each setting.
In practice, it often seems to be the case that the value of each variable in a causal network is determined by the values of at most k other variables, where k is relatively small. And when some variable does depend on quite a few other variables, we can sometimes get away with ignoring many of these variables because their impact is relatively small. Alternatively, we can hope that, if the value of a variable depends on that of many variables, the dependence is a simple one, as in the case of the headache example above, so that it can be described by a short equation, perhaps with a few special cases. To take just one example, consider voting. The outcome of a vote may well depend on how each voter votes, and there can be many voters. But voting rules can typically be described by relatively simple equations (majority rules; if there are more than two candidates, someone must get more than 50% of the vote or there is a runoff; no more than 20% can abstain; …).
The bottom line here is that it seems likely that, just as with the probability distributions that arise in practice, the structural equations that arise in practice are likely to have compact representations. Of course, this is a statement that needs to be experimentally verified. But it is worth pointing out that in all the examples given in this book, the equations can be represented compactly.
These compact representations have an added benefit. Recall that in Section 2.5, where I discussed adding probability to structural equations, I pointed out that it was useful to have a natural way to represent certain probabilistic facts. Bayesian networks go a long way to helping in this regard. However, they are not a complete solution. For example, there is no natural way to represent in a Bayesian network the fact that counterfactual outcomes such as “the bottle would have toppled over had only Suzy’s rock hit it” and “the bottle would have toppled over had only Billy’s rock hit it” are independent (see Example 2.5.4), using only the variables we have used for the rock-throwing example so far. However, if we add variables SO and BO to the model that characterize whether the bottle would have toppled over if Suzy (resp., Billy) had hit it, and take these variables to be determined by the context, then we can easily say that these two outcomes are independent. Even with the variables used in Example 2.5.4, we can say, for example, that Billy throwing and Suzy throwing are independent events. Of course, it is not at all clear that these variables are independent; it is easy to imagine that Suzy throwing can influence Billy throwing, and vice versa, so it is more likely that both throw than that only one of them throws. The point is that using a Bayesian network, we can represent these probabilistic independencies. Not surprisingly, here too the choice of variables used to describe the model can make a big difference.
5.2 Compact Representations of the Normality Ordering
I now turn to the problem of representing a normality ordering compactly. There are two main ideas. We have already seen the first: taking advantage of independencies. Although we used a partial preorder ⪰ to represent the normality ordering, not probability, it turns out that the “technology” of Bayesian networks can be applied far more broadly than just probability; we just need a structure that has a number of minimal properties and an analogue of (conditional) independence. Somewhat surprisingly perhaps, it turns out that partial preorders fit the bill.
The second idea can be applied if the normality ordering largely reflects the causal structure in the sense that what is normal is what agrees with the equations. An example should make this point clearer: Suppose that the causal structure is such that if the patient suffers a head trauma, then he would also suffer from headaches. Then we would expect a world where the patient has a headache and a trauma to be more normal, all else being equal, than a world in which the patient has a trauma and does not have a headache. In this way, a representation of causal structure can do “double duty” by representing much of the normality order as well.
In the remainder of this section, I discuss these ideas in more detail. I remark that although I talk about a partial preorder on worlds in this section, these ideas apply equally well to the alternate representation of normality that involves a partial preorder on contexts. Since a context ![[image]](images/eqn68.jpg) can be identified with the world
can be identified with the world ![[image]](images/eqn412.jpg) , a partial preorder on worlds induces a partial preorder on contexts and vice versa (although not all worlds may be of the form
, a partial preorder on worlds induces a partial preorder on contexts and vice versa (although not all worlds may be of the form ![[image]](images/eqn412.jpg) for some context
for some context ![[image]](images/eqn68.jpg) ).
).
5.2.1 Algebraic plausibility measures: the big picture
Probability measures are just one way of representing uncertainty; many other representations of uncertainty have been discussed in the literature. In particular, many of the representations of typicality and normality mentioned in the bibliographic notes for Chapter 3 can be viewed as representations of uncertainty. This includes partial preorders; one way of interpreting s ⪰ s′ is that the world s is more likely than the world s′. Plausibility measures are generalized representations of uncertainty; probability and all the representations of uncertainty mentioned in the notes of Chapter 3 are instances of plausibility measures.
The basic idea behind plausibility measures is straightforward. A probability measure on a finite set W of worlds maps subsets of W to [0, 1]. A plausibility measure is more general; it maps subsets of W to some arbitrary set D partially ordered by ≤. If Pl is a plausibility measure, then Pl(U) denotes the plausibility of U. If Pl(U) ≤ Pl(V), then V is at least as plausible as U. Because the order is partial, it could be that the plausibility of two different sets is incomparable. An agent may not be prepared to order two sets in terms of plausibility. D is assumed to contain two special elements, ⊥ and ⊤, such that ⊥ ≤ d ≤ ⊤ for all d ∈ D. We require that Pl(∅) = ⊥ and Pl(W) = ⊤. Thus, ⊥ and ⊤ are the analogues of 0 and 1 for probability. We further require that if U ⊆ V, then Pl(U) ≤ Pl(V). This seems reasonable; a superset of U should be at least as plausible as U. Since we want to talk about conditional independence here, we will need to deal with what have been called conditional plausibility measures (cpms), not just plausibility measures. A conditional plausibility measure maps pairs of subsets of W to some partially ordered set D. I write Pl(U | V) rather than Pl(U, V), in keeping with standard notation for conditioning. I typically write just Pl(U) rather than Pl(U | W) (so unconditional plausibility is identified with conditioning on the whole space).
In the case of a probability measure Pr, it is standard to take Pr(U | V) to be undefined if Pr(V) = 0. In general, we must make precise what the allowable second arguments of a cpm are. For simplicity here, I assume that Pl(U | V) is defined as long as V ≠ ∅. For each fixed V ≠ ∅, Pl(•| V) is required to be a plausibility measure on W. More generally, the following properties are required:
CPl1. Pl(∅ | V) = ⊥.
CPl2. Pl(W | V) = ⊤.
CPl3. If U ⊆ U′, then Pl(U | V) ≤ Pl(U′ | V).
CPl4. Pl(U | V) = Pl(U ∩ V | V).
CPl1 and CPl2 just say that the empty set has plausibility ⊥ and the whole space has plausibility, conditional on any set V. These are the obvious analogues of the requirements for conditional probability that the empty set has probability 0 and the whole space probability 1, conditional on any set. CPl3 just says that the plausibility of a superset cannot be less than the plausibility of a subset. (Note that this means that these plausibilities are comparable; in general, the plausibilities of two sets may be incomparable.) Finally, CPl4 just says that the plausibility U conditional on V depends only on the part of U in V.
There are some other obvious properties we might want to require, such as generalizations of CPl1 and CPl2 that say that Pl(U | V) = ⊥ if U ∩ V = ∅ and Pl(U | V) = ⊤ if V ⊆ U. In the case of conditional probability, the analogues of these properties follow from the fact that Pr(V1 ∪ V2 | V) = Pr(V1 | V) + Pr(V2 | V) if V1 and V2 are disjoint sets. Another important property of conditional probability is that Pr(U | V′) = Pr(U | V) × Pr(V | V′) if U ⊆ V ⊆ V′. These properties turn out to play a critical role in guaranteeing compact representations of probability distributions, so we will need plausibilistic analogues of them. This means that we need to have plausibilistic analogues of addition and multiplication so that we can take
![[image]](images/eqn517.jpg) (5.1)
(5.1)
A cpm that satisfies these properties is said to be an algebraic cpm. (I give a more formal definition in Section 5.5.1.) Of course, for probability, (5.1) holds if we take ⊕ and ⊗ to be + and ×, respectively. I mentioned in the notes to Chapter 3 that another approach to giving semantics to normality and typicality uses what are called ranking functions; (5.1) holds for ranking functions if we take ⊕ and ⊗ to be min and +, respectively.
Both the original and alternative approach to incorporating normality are based on a partial preorder. In the original approach, it is a partial preorder on worlds, whereas in the alternative approach, it is a partial preorder on contexts, which is lifted to a partial preorder on sets of contexts. We would like to be able to view these partial preorders as algebraic cpms. There is a problem though. A plausibility measure attaches a plausibility to sets of worlds, not single worlds. This is compatible with the alternative approach, for which an ordering on events was critical. Indeed, when defining the alternative approach, I showed how a partial preorder ⪰ on contexts can be extended to a partial preorder on ⪰e sets of contexts. This order on sets essentially defines a plausibility measure. But I need even more here. I want not just an arbitrary plausibility measure but an algebraic cpm. Getting an appropriate algebraic cpm involves some technical details, so I defer the construction to Appendix 5.5.1. For the purposes of this section, it suffices to just accept that this can be done; specifically, assume that a partial preorder on worlds (or contexts) can be extended to an algebraic cpm defined on sets of worlds (or contexts). The key point is that, once we do this, we can talk about the independence and conditional independence of endogenous variables, just as in the case of probability. Moreover, it means that the normality ordering can be represented using the analogue of a causal network, where again a node labeled by X is conditionally independent of all its ancestors in the graph given its parents (just as BS is independent of BT given BH). This will allow us to apply the “technology” of Bayesian networks to the normality ordering almost without change. Although the graph will, in general, be different from the graph representing the (structural equations of) the causal model, in many cases, there will be substantial overlap between the two. As discussed in Section 5.2.2, this allows for even greater representational economy.
Although this is helpful, in a sense, it is the “wrong” result. This result says that if we have a partial preorder on worlds, it can be represented compactly. But the real question is how do agents come up with a normality ordering in the first place? To understand the point, consider a lawyer arguing that a defendant should be convicted of arson. The lawyer will attempt to establish a claim of actual causation: that the defendant’s action of lighting a match was an actual cause of the forest fire. To do this, she will need to convince the jury that a certain extended causal model is correct and that certain initial conditions obtained (for example, that the defendant did indeed light a match). To justify the causal model, she will need to defend the equations. This might involve convincing the jury that the defendant’s match was the sort of thing that could cause a forest fire (the wood was dry), and that there would have been no fire in the absence of some triggering event, such as a lightning strike or an act of arson.
The lawyer will also have to defend a normality ordering. To do this, she might argue that a lightning strike could not have been reasonably foreseen, that lighting a fire in the forest at that time of year was in violation of a statute, and that it was to be expected that a forest fire would result from such an act. It will usually be easier to justify a normality ordering in a piecemeal fashion. Instead of arguing for a particular normality ordering on entire worlds, she argues that individual variables typically take certain values in certain situations. By defining the normality ordering for a variable (or for a variable conditional on other variables taking on certain values) and making some independence assumptions, we can completely characterize the normality ordering.
The idea is that if a situation is characterized by the random variables X1,…, Xn, so that a world has the form (x1,…, xn), then we assume that each world has a plausibility value of the form a1 ⊗⋯⊗ an. For example, if n = 3, X1 and X2 are independent, and X3 depends on both X1 and X2, then a world (1, 0, 1) would be assigned a plausibility of a1 ⊗ a2 ⊗ a3, where a1 is the unconditional plausibility of X1 = 1, a2 is the unconditional plausibility of X2 = 0, and a3 is the plausibility of X3 = 1 conditional on X1 = 1 ∩ X2 = 0. We do not need to actually define the operation ⊗; we just leave a1 ⊗ a2 ⊗ a3 as an uninterpreted expression. However, if we have some constraints on the relative order of elements (as we do in our example and typically will in practice), then we can lift this to an order on expressions of the form a1 ⊗ a2 ⊗ a3 by taking ![[image]](images/eqn518.jpg) if and only if, for all ai, there is a distinct
if and only if, for all ai, there is a distinct ![[image]](images/eqn519.jpg) such that
such that ![[image]](images/eqn520.jpg) . The “only if” builds in a minimality assumption: two elements a1 ⊗ a2 ⊗ a3 and
. The “only if” builds in a minimality assumption: two elements a1 ⊗ a2 ⊗ a3 and ![[image]](images/eqn521.jpg) are incomparable unless they are forced to be comparable by the ordering relations among the ais and the
are incomparable unless they are forced to be comparable by the ordering relations among the ais and the ![[image]](images/eqn522.jpg) . One advantage of using a partial preorder, rather than a total preorder, is that we can do this.
. One advantage of using a partial preorder, rather than a total preorder, is that we can do this.
Although this may all seem rather mysterious, the application of these ideas to specific cases is often quite intuitive. The following two examples show how this construction works in our running example.
Example 5.2.1 Consider the forest-fire example again. We can represent the independencies in the forest-fire example using the causal network given in Figure 5.1 (where the exogenous variable is omitted): L and MD are independent, and FF depends on both of them. Thus, we do indeed have a compact network describing the relevant (in)dependencies. Note that the same network represents the (in)dependencies in both the conjunctive and disjunctive models.
![[image]](images/fig5-1.jpg)
Figure 5.1: The forest-fire example.
For the remainder of this example, for definiteness, consider the disjunctive model, where either a lightning strike or an arsonist’s match suffices for fire. It would be natural to say that lightning strikes and arson attacks are atypical, and that a forest fire typically occurs if either of these events occurs. Suppose that we use ![[image]](images/eqn523.jpg) to represent the plausibility of L = 0 (lightning not occurring) and
to represent the plausibility of L = 0 (lightning not occurring) and ![[image]](images/eqn524.jpg) to represent the plausibility of L = 1; similarly, we use
to represent the plausibility of L = 1; similarly, we use ![[image]](images/eqn525.jpg) to represent the plausibility of MD = 0 and
to represent the plausibility of MD = 0 and ![[image]](images/eqn526.jpg) to represent the plausibility of MD = 1. Now the question is what we should take the conditional plausibility of FF = 0 and FF = 1 to be, given each of the four possible settings of L and MD. For simplicity, take all the four values compatible with the equations to be equally plausible, with plausibility
to represent the plausibility of MD = 1. Now the question is what we should take the conditional plausibility of FF = 0 and FF = 1 to be, given each of the four possible settings of L and MD. For simplicity, take all the four values compatible with the equations to be equally plausible, with plausibility ![[image]](images/eqn527.jpg) . Then using Pl to represent the plausibility measure, we have:
. Then using Pl to represent the plausibility measure, we have:
![[image]](images/eqn528.jpg) (5.2)
(5.2)
Suppose that we further assume that ![[image]](images/eqn529.jpg) ,
, ![[image]](images/eqn530.jpg) , and
, and ![[image]](images/eqn531.jpg) are all incomparable, as are
are all incomparable, as are ![[image]](images/eqn532.jpg) ,
, ![[image]](images/eqn533.jpg) , and
, and ![[image]](images/eqn534.jpg) . Thus, for example, we cannot compare the degree of typicality of no lightning with that of no arson attacks or the degree of atypicality of lightning with that of an arson attack. Using the construction discussed gives us the ordering on worlds given in Figure 5.2, where an arrow from w to w′ indicates that w′ ≻ w.
. Thus, for example, we cannot compare the degree of typicality of no lightning with that of no arson attacks or the degree of atypicality of lightning with that of an arson attack. Using the construction discussed gives us the ordering on worlds given in Figure 5.2, where an arrow from w to w′ indicates that w′ ≻ w.
In this normality ordering, (0, 1, 1) is more normal than (1, 1, 1) and (0, 0, 1) but incomparable with (1, 0, 0) and (0, 0, 1). That is because, according to our construction, (0, 1, 1), (1, 1, 1), (0, 1, 0), (1, 0, 0), and (0, 0, 1) have plausibility ![[image]](images/eqn535.jpg) ,
, ![[image]](images/eqn536.jpg) , and
, and ![[image]](images/eqn539.jpg) , respectively. The fact that
, respectively. The fact that ![[image]](images/eqn540.jpg) follows because
follows because ![[image]](images/eqn541.jpg) . The fact that we have >, not just ≥, follows from the fact that we do not have
. The fact that we have >, not just ≥, follows from the fact that we do not have ![[image]](images/eqn542.jpg) ; it does not follow from our condition from comparability. The other comparisons follow from similar arguments. For example, the fact that (0, 1, 1) is incomparable with (1, 0, 0) follows because neither
; it does not follow from our condition from comparability. The other comparisons follow from similar arguments. For example, the fact that (0, 1, 1) is incomparable with (1, 0, 0) follows because neither ![[image]](images/eqn543.jpg) follows from our conditions. ■
follows from our conditions. ■
Example 5.2.1 shows how the “Bayesian network technology” can be used to compute all the relevant plausibilities (and thus the normality ordering). To go from the qualitative representation of (in)dependencies in terms of a causal network to a more quantitative representation, we need the conditional plausibility of the value of each variable given each possible setting of its parents. For variables that have no parents, this amounts to giving the unconditional plausibility of each of the values of the variable. This is exactly what is done on the first two lines of Table (5.2) for the variables L and MD, which have no parents in the causal network (other than the exogenous variable). The next four lines of Table (5.2) give the plausibility of the two values of FF, conditional on the four possible settings of its parents in the network, L and MD. As is shown in the rest of the discussion in the example, these values suffice to compute all the relevant plausibilities.
![[image]](images/fig5-2.jpg)
Figure 5.2: A normality order on worlds.
Although the savings in this case is not so great, the savings can be quite significant if we have larger models. If there are n binary variables, and each one has at most k parents, rather than describing the plausibility of the 2n worlds, we need to give, for each variable, at most 2k+1 plausibilities (the plausibility of each value of the variable conditional on each of the 2k possible settings of values for its parents). Thus, we need at most n2k+1 plausibilities. Of course, this is not much of a savings if k is close to n, but if k is relatively small and n is large, then n2k+1 is much smaller than 2n. For example, if k = 5 and n = 100 (quite realistic numbers for a medical example; indeed, n may be even larger), then n2k+1 = 6, 400, while 2n = 2100 > 1033. In general, we have to consider all the ways of ordering these 6, 400 (or 2100!) plausibility values, but as the discussion in the example shows, the additional assumptions on the ordering of expressions of the form a1 ⊗⋯⊗ an makes this straightforward (and easy to represent) as well.
Example 5.2.2 The preorder on worlds induced by the Bayesian network in the previous example treats the lightning and the arsonist’s actions as incomparable. For example, the world (1, 0, 1), where lightning strikes, the arsonist doesn’t, and there is a fire, is incomparable with the world where lightning doesn’t strike, the arsonist lights his match, and the fire occurs. But this is not the only possibility. Suppose we judge that it would be more atypical for the arsonist to light a fire than for lightning to strike and also more typical for the arsonist not to light a fire than for lightning not to strike. (Unlike the case of probability, the latter does not follow from the former.) Recall that this order might reflect the fact that arson is illegal and immoral, rather than the frequency of occurrence of arson as opposed to lightning. Although Table (5.2) still describes the conditional plausibility relations, we now have ![[image]](images/eqn544.jpg) and
and ![[image]](images/eqn545.jpg) . This gives us the ordering on worlds described in Figure 5.3.
. This gives us the ordering on worlds described in Figure 5.3.
![[image]](images/fig5-3.jpg)
Figure 5.3: A different normality ordering on worlds.
Now, for example, the world (0, 1, 1) is strictly more normal than the world (1, 0, 1); again, the former has plausibility ![[image]](images/eqn546.jpg) , whereas the latter has plausibility
, whereas the latter has plausibility ![[image]](images/eqn547.jpg) . But since
. But since ![[image]](images/eqn548.jpg) and
and ![[image]](images/eqn549.jpg) , by assumption, it follows that
, by assumption, it follows that ![[image]](images/eqn550.jpg) . ■
. ■
5.2.2 Piggy-backing on the causal model
As I noted earlier, the graph representing the normality ordering can, in general, be different from that representing the causal model. Nonetheless, in many cases there will be substantial agreement between them. When this happens, it will be possible to make parts of the causal model do “double duty”: representing both the causal structure and the structure of the normality ordering. In Examples 5.2.1 and 5.2.2, the graph describing the causal structure is the same as that representing the normality ordering. We assumed that L and MD were independent with regard to both the structural equations and normality, but that FF depended on both L and MD. In the case of the structural equations, the independence of L and MD means that, once we set all other variables, a change in the value of L cannot affect the value of MD, and vice versa. In the case of normality, it means that the degree of normality of a world where lightning occurred (resp., did not occur) does not affect the degree of normality of a world where the arsonist dropped a match (resp., did not drop a match), and vice versa.
But we can say something more “quantitative”, beyond just the qualitative statement of independence. Consider the entries for the conditional plausibility of variable FF from Table (5.2), which can be summarized as follows:
![[image]](images/eqn551.jpg)
Recall that FF = max(L, MD) is the structural equation for FF in the causal model. So the conditional plausibility table says, in effect, that it is typical for FF to obey the structural equations and atypical to violate it.
Variables typically obey the structural equations. Thus, it is often far more efficient to assume that this holds by default, and explicitly enumerate cases where this is not so, rather than writing out all the equations. Consider the following default rule.
Default Rule 1 (Normal Causality): Let X be a variable in a causal model with no exogenous parents, and let ![[image]](images/eqn552.jpg) be the vector of parents of X. Let the structural equation for X be
be the vector of parents of X. Let the structural equation for X be ![[image]](images/eqn553.jpg) . Then, unless explicitly given otherwise, there are two plausibility values
. Then, unless explicitly given otherwise, there are two plausibility values ![[image]](images/eqn554.jpg) and
and ![[image]](images/eqn555.jpg) with
with ![[image]](images/eqn556.jpg) such that
such that
![[image]](images/eqn557.jpg)
Default Rule 1 says that it is typical for variables to satisfy the equations unless we explicitly stipulate otherwise. Moreover, it says that, by default, all values of variables that satisfy the equations are equally typical, whereas all those that do not satisfy the equations are equally atypical. In Examples 5.2.1 and 5.2.2, FF satisfies Default Rule 1. Of course, we could allow some deviations from the equations to be more atypical than others; this would be a violation of the default rule. As the name suggests, the default rule is to be assumed unless explicitly stated otherwise. The hope is that there will be relatively few violations, so there is still substantial representational economy in assuming the rule. That is, the hope is that, once a causal model is given, the normality ordering can be represented efficiently by providing the conditional plausibility tables for only those variables that violate the default rule, or whose plausibility values are not determined by the default rule (because they have exogenous parents). It may, of course, be possible to formulate more complex versions of Default Rule 1 that accommodate exogenous parents and allow for more than two default values. The rule as stated seems like a reasonable compromise between simplicity and general applicability.
The Normal Causality rule, by itself, does not tell us how the plausibility values for one variable compare to the plausibility values for another variable. Default Rule 1 can be supplemented with a second rule:
Default Rule 2 (Minimality): If dx and dy are plausibility values for distinct variables X and Y, and no information is given explicitly regarding the relative orders of dx and dy, then dx and dy are incomparable.
Again, this default rule is assumed to hold only if there is no explicit stipulation to the contrary. Default Rule 2 says that the normality ordering among possible worlds should not include any comparisons that do not follow from the equations (via Default Rule 1) together with the information that is explicitly given. Interestingly, in the context of probability, a distribution that maximizes entropy subject to some constraints is the one that (very roughly) makes things “as equal as possible” subject to the constraints. If there are no constraints, it reduces to the classic principle of indifference, which assigns equal probability to different possibilities in the absence of any reason to think some are more probable. In the context of plausibility, where only a partial order is assigned, it is possible to push this idea a step further by making the possibilities incomparable. In Example 5.2.1, all three variables satisfy Minimality. In Example 5.2.2, FF satisfies Minimality with respect to the other two variables, but the variables L and MD do not satisfy it with respect to one another (since their values are stipulated to be comparable).
With these two default rules, the extended causal model for the disjunctive model of the forest fire can be represented succinctly as follows:
The rest of the structure of the normality ordering follows from the default rules.
The extended causal model in Example 5.2.2 can be represented just using the following equations and inequalities:
Again, the rest of the structure follows from the default rules. In each case, the normality ordering among the eight possible worlds can be represented with the addition of just a few plausibility values to the causal model. Thus, moving from a causal model to an extended causal model need not impose enormous cognitive demands.
Exceptions to the default rules can come in many forms. There could be values of the variables for which violations of the equations are more typical than agreements with the equations. As was suggested after Default Rule 1, there could be multiple values of typicality, rather than just two for each variable. Or the conditional plausibility values of one variable could be comparable with those of another variable. These default rules are useful to the extent that there are relatively few violations of them. For some settings, other default rules may also be useful; the two rules above are certainly not the only possible useful defaults.
Given these examples, the reader may wonder whether the causal structure is always identical to the normality ordering. It is easy to see that there are counterexamples to this. Recall the Knobe and Fraser experiment from Section 3.1, in which Professor Smith and the administrative assistant took the two remaining pens. Suppose that we modify the example slightly by assuming that the department chair has the option of instituting a policy forbidding faculty members from taking pens. Further suppose that Professor Smith will ignore the policy even if it is instituted and take a pen if he needs. it. We can model this story using the binary variables CP (which is 1 if the chairman institutes the policy and 0 otherwise), PS (which is 1 if Professor Smith takes the pen and 0 otherwise), and PO (which is 1 if a problem occurs and 0 otherwise). Now, by assumption, as far as the causal structures goes, PS is independent of CP: Professor Smith takes the pen regardless of whether there is a policy. However, as far as the normality ordering goes, PS does depend on CP.
5.3 The Complexity of Determining Causality
In this section I discuss the computational complexity of determining causality. It seems clear that the modified definition is conceptually simpler than the original and updated HP definition. This conceptual simplicity has a technical analogue: in a precise sense, it is simpler to determine whether ![[image]](images/eqn558.jpg) is a cause of φ according to the modified definition than it is for either the original or updated HP definitions.
is a cause of φ according to the modified definition than it is for either the original or updated HP definitions.
To make this precise, I need to review some basic notions of complexity theory. Formally, we are interested in describing the difficulty of determining whether a given x is an element of a set L (sometimes called a language). The language of interest here is
![[image]](images/eqn559.jpg)
We will be interested in the difficulty of determining whether a particular tuple is in ![[image]](images/eqn560.jpg) .
.
How do we characterize the difficulty of determining whether a particular tuple is in ![[image]](images/eqn561.jpg) We expect the problem of determining whether a tuple
We expect the problem of determining whether a tuple ![[image]](images/eqn562.jpg) is in
is in ![[image]](images/eqn565.jpg) to be harder if the tuple is larger; intuitively, the problem should be harder for larger causal models M than for smaller models. The question is how much harder. The complexity class P (polynomial time) consists of all languages
to be harder if the tuple is larger; intuitively, the problem should be harder for larger causal models M than for smaller models. The question is how much harder. The complexity class P (polynomial time) consists of all languages ![[image]](images/eqn566.jpg) such that determining if x is in
such that determining if x is in ![[image]](images/eqn567.jpg) can be done in time that is a polynomial function of the size of x (where the size of x is just the length of x, viewed as a string of symbols). Typically, languages for which membership can be determined in polynomial time are considered tractable. Similarly, PSPACE (polynomial space) consists of all languages for which membership can be determined in space polynomial in the input size, and EXPTIME consists of all languages for which membership can be determined in time exponential in the input size.
can be done in time that is a polynomial function of the size of x (where the size of x is just the length of x, viewed as a string of symbols). Typically, languages for which membership can be determined in polynomial time are considered tractable. Similarly, PSPACE (polynomial space) consists of all languages for which membership can be determined in space polynomial in the input size, and EXPTIME consists of all languages for which membership can be determined in time exponential in the input size.
The class NP consists of those languages for which membership can be determined in non-deterministic polynomial time. A language ![[image]](images/eqn568.jpg) is in NP if a program that makes some guesses can determine membership in
is in NP if a program that makes some guesses can determine membership in ![[image]](images/eqn569.jpg) in polynomial time. The classic language in NP is the language consisting of all satisfiable propositional formulas (i.e., formulas satisfied by some truth assignment). We can determine whether a formula is satisfiable by guessing a satisfying truth assignment; after guessing a truth assignment, it is easy to check in polynomial time that the formula is indeed satisfied by that truth assignment.
in polynomial time. The classic language in NP is the language consisting of all satisfiable propositional formulas (i.e., formulas satisfied by some truth assignment). We can determine whether a formula is satisfiable by guessing a satisfying truth assignment; after guessing a truth assignment, it is easy to check in polynomial time that the formula is indeed satisfied by that truth assignment.
The class co-NP consists of all languages whose complement is in NP. For example, the language consisting of all unsatisfiable propositional formulas is in co-NP because its complement, the set of satisfiable propositional formulas, is in NP. Similarly, the set of valid propositional formulas is in co-NP.
It can be shown that the following is an equivalent definition of NP: a language ![[image]](images/eqn570.jpg) is in NP iff there is a polynomial-time algorithm A that takes two arguments, x and y, such that
is in NP iff there is a polynomial-time algorithm A that takes two arguments, x and y, such that ![[image]](images/eqn571.jpg) iff there exists a y such that A(x, y) = 1. We can think of y as representing the “guess”. For example, if
iff there exists a y such that A(x, y) = 1. We can think of y as representing the “guess”. For example, if ![[image]](images/eqn572.jpg) is the language of satisfiable propositional formulas, x represents a propositional formula, y is a truth assignment, and A(x, y) = 1 if the truth assignment y satisfies x. It is easy to see that x is satisfiable iff there is some y such that A(x, y) = 1. Moreover, A is certainly polynomial time. Similarly, a language
is the language of satisfiable propositional formulas, x represents a propositional formula, y is a truth assignment, and A(x, y) = 1 if the truth assignment y satisfies x. It is easy to see that x is satisfiable iff there is some y such that A(x, y) = 1. Moreover, A is certainly polynomial time. Similarly, a language ![[image]](images/eqn573.jpg) is in co-NP iff there is a polynomial-time algorithm A that takes two arguments, x and y, such that
is in co-NP iff there is a polynomial-time algorithm A that takes two arguments, x and y, such that ![[image]](images/eqn574.jpg) iff, for all y, we have A(x, y) = 1. For validity, we can again take x to be a formula and y to be a truth assignment. Now x is valid iff A(x, y) = 1 for all truth assignments y.
iff, for all y, we have A(x, y) = 1. For validity, we can again take x to be a formula and y to be a truth assignment. Now x is valid iff A(x, y) = 1 for all truth assignments y.
The polynomial hierarchy is a hierarchy of complexity classes that generalize NP and co-NP. We take ![[image]](images/eqn575.jpg) to be NP.
to be NP. ![[image]](images/eqn576.jpg) consists of all languages
consists of all languages ![[image]](images/eqn577.jpg) for which there exists a polynomial-time algorithm A that takes three arguments such that
for which there exists a polynomial-time algorithm A that takes three arguments such that ![[image]](images/eqn578.jpg) iff there exists y1 such that for all y2 we have (x, y1, y2) = 1. To get
iff there exists y1 such that for all y2 we have (x, y1, y2) = 1. To get ![[image]](images/eqn579.jpg) , we consider algorithms that take four arguments and use one more alternation of quantifiers (there exists y1 such that for all y2 there exists y3). We can continue alternating quantifiers in this way to define
, we consider algorithms that take four arguments and use one more alternation of quantifiers (there exists y1 such that for all y2 there exists y3). We can continue alternating quantifiers in this way to define ![[image]](images/eqn580.jpg) for all k. We can similarly define
for all k. We can similarly define ![[image]](images/eqn581.jpg) , this time starting the alternation with a universal quantifier (for all y1, there exists y2, such that for all y3 …). Finally, the set
, this time starting the alternation with a universal quantifier (for all y1, there exists y2, such that for all y3 …). Finally, the set ![[image]](images/eqn582.jpg) is defined as follows:
is defined as follows:
![[image]](images/eqn583.jpg)
That is, ![[image]](images/eqn584.jpg) consists of all languages (sets) that can be written as the intersection of a language in
consists of all languages (sets) that can be written as the intersection of a language in ![[image]](images/eqn585.jpg) and a language in
and a language in ![[image]](images/eqn586.jpg) .
.
We can think of NP as consisting of all languages ![[image]](images/eqn587.jpg) such that if
such that if ![[image]](images/eqn588.jpg) , then there is a short proof demonstrating this fact (although the proof may be hard to find). Similarly, co-NP consists of those languages
, then there is a short proof demonstrating this fact (although the proof may be hard to find). Similarly, co-NP consists of those languages ![[image]](images/eqn589.jpg) such that if
such that if ![[image]](images/eqn590.jpg) , then there is a short proof demonstrating this fact. Thus,
, then there is a short proof demonstrating this fact. Thus, ![[image]](images/eqn591.jpg) consists of all languages
consists of all languages ![[image]](images/eqn592.jpg) such that for all x, there is a short proof of whichever of
such that for all x, there is a short proof of whichever of ![[image]](images/eqn593.jpg) and
and ![[image]](images/eqn594.jpg) is true.
is true. ![[image]](images/eqn595.jpg) generalizes these ideas to higher levels of the polynomial hierarchy. Classifying a language
generalizes these ideas to higher levels of the polynomial hierarchy. Classifying a language ![[image]](images/eqn596.jpg) in terms of which complexity class it lies in helps us get an idea of how difficult it is to determine membership in
in terms of which complexity class it lies in helps us get an idea of how difficult it is to determine membership in ![[image]](images/eqn597.jpg) . It is remarkable how many naturally defined languages can be characterized in terms of these complexity classes.
. It is remarkable how many naturally defined languages can be characterized in terms of these complexity classes.
Note that if a complexity class C1 is a subset of complexity class C2, then every language in C1 is in C2; hence, C2 represents problems that are at least as hard as C1. It is not hard to show that
![[image]](images/eqn598.jpg)
It is known that P ≠ EXPTIME (so that, in general, the problem determining set membership for a language in EXPTIME is strictly harder than the corresponding problem for a language in P, but it is not known whether any of the other inclusions is strict (although it is conjectured that they all are).
We can get a similar chain of inequalities by replacing NP and ![[image]](images/eqn599.jpg) by co-NP and
by co-NP and ![[image]](images/eqn600.jpg) . Finally, it is not hard to show that
. Finally, it is not hard to show that
![[image]](images/eqn601.jpg)
For example, to see that ![[image]](images/eqn602.jpg) , take
, take ![[image]](images/eqn603.jpg) in the definition of
in the definition of ![[image]](images/eqn604.jpg) to be the universal set, so that
to be the universal set, so that ![[image]](images/eqn605.jpg) . (The argument that
. (The argument that ![[image]](images/eqn606.jpg) is essentially the same.) Thus,
is essentially the same.) Thus, ![[image]](images/eqn607.jpg) represents problems that are at least as hard as each of
represents problems that are at least as hard as each of ![[image]](images/eqn608.jpg) and
and ![[image]](images/eqn609.jpg) but no harder than either of
but no harder than either of ![[image]](images/eqn610.jpg) and
and ![[image]](images/eqn611.jpg) . It is perhaps worth noting that although, by definition, a language is in
. It is perhaps worth noting that although, by definition, a language is in ![[image]](images/eqn612.jpg) if it can be written as the intersection of languages in
if it can be written as the intersection of languages in ![[image]](images/eqn613.jpg) and
and ![[image]](images/eqn614.jpg) , this is very different from saying that
, this is very different from saying that ![[image]](images/eqn615.jpg) .
.
We need one more set of definitions: a language ![[image]](images/eqn616.jpg) is said to be hard with respect to a complexity class
is said to be hard with respect to a complexity class ![[image]](images/eqn617.jpg) (e.g., NP-hard, PSPACE-hard, etc.) if every language in
(e.g., NP-hard, PSPACE-hard, etc.) if every language in ![[image]](images/eqn618.jpg) can be efficiently reduced to
can be efficiently reduced to ![[image]](images/eqn619.jpg) ; that is, for every language
; that is, for every language ![[image]](images/eqn620.jpg) in
in ![[image]](images/eqn621.jpg) an algorithm deciding membership in
an algorithm deciding membership in ![[image]](images/eqn622.jpg) can be easily obtained from an algorithm for deciding membership in
can be easily obtained from an algorithm for deciding membership in ![[image]](images/eqn623.jpg) . More precisely, this means that there is a polynomial-time computable function f such that
. More precisely, this means that there is a polynomial-time computable function f such that ![[image]](images/eqn624.jpg) iff
iff ![[image]](images/eqn625.jpg) . Thus, given an algorithm
. Thus, given an algorithm ![[image]](images/eqn626.jpg) for deciding membership in
for deciding membership in ![[image]](images/eqn627.jpg) , we can decide whether
, we can decide whether ![[image]](images/eqn628.jpg) by running
by running ![[image]](images/eqn629.jpg) on input f (x). Finally, a language is said to be complete with respect to a complexity class
on input f (x). Finally, a language is said to be complete with respect to a complexity class ![[image]](images/eqn630.jpg) , or
, or ![[image]](images/eqn631.jpg) -complete, if it is both in
-complete, if it is both in ![[image]](images/eqn632.jpg) and
and ![[image]](images/eqn633.jpg) -hard. It is well known that Sat, the language consisting of all satisfiable propositional formulas, is NP-complete. It easily follows that its complement Satc, which consists of all propositional formulas that are not satisfiable (i.e., negations of formulas that are valid), is co-NP-complete.
-hard. It is well known that Sat, the language consisting of all satisfiable propositional formulas, is NP-complete. It easily follows that its complement Satc, which consists of all propositional formulas that are not satisfiable (i.e., negations of formulas that are valid), is co-NP-complete.
Although the complexity classes in the polynomial hierarchy are somewhat exotic, they are exactly what we need to characterize the complexity of determining causality. The exact complexity depends on the definition used. The problem is easiest with the modified definition; roughly speaking, this is because we do not have to deal with AC2(bo) or AC2(bu). Since, with the original definition, causes are always single conjuncts, the original definition is easier to deal with than the updated definition. Again, this shouldn’t be too surprising, since there is less to check.
Before making these claims precise, there is another issue that must be discussed. Recall that when we talk about the complexity of determining whether ![[image]](images/eqn634.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dclimg0139.jpg) , formally, we consider how hard it is to decide whether the tuple (M,
, formally, we consider how hard it is to decide whether the tuple (M, ![[image]](images/eqn635.jpg) , φ,
, φ, ![[image]](images/eqn636.jpg) ,
, ![[image]](images/eqn637.jpg) ) is in the language
) is in the language ![[image]](images/eqn638.jpg) . In light of the discussion in Sections 5.1, we need to be careful about how M is represented. If we represent M naively, then its description can be exponential in the signature
. In light of the discussion in Sections 5.1, we need to be careful about how M is represented. If we represent M naively, then its description can be exponential in the signature ![[image]](images/eqn639.jpg) (in particular, exponential in the length of φ, the number of endogenous variables in
(in particular, exponential in the length of φ, the number of endogenous variables in ![[image]](images/eqn640.jpg) , and the cardinality of the range of these variables). It is not hard to see that all the relevant calculations are no worse than exponential in the length of φ, the number of endogenous variables, and the cardinality of their ranges, so the calculation becomes polynomial in the size of the input. This makes the problem polynomial for what are arguably the wrong reasons. The size of the input is masking the true complexity of the problem. Here, I assume that the causal model can be described succinctly. In particular, I assume that succinct expressions for equations are allowed in describing the model, as I have been doing all along. Thus, for example, the equation for BS in the “sophisticated” model
, and the cardinality of the range of these variables). It is not hard to see that all the relevant calculations are no worse than exponential in the length of φ, the number of endogenous variables, and the cardinality of their ranges, so the calculation becomes polynomial in the size of the input. This makes the problem polynomial for what are arguably the wrong reasons. The size of the input is masking the true complexity of the problem. Here, I assume that the causal model can be described succinctly. In particular, I assume that succinct expressions for equations are allowed in describing the model, as I have been doing all along. Thus, for example, the equation for BS in the “sophisticated” model ![[image]](images/eqn641.jpg) for the rock-throwing example is given as BS = BH ∨ SH, rather than explicitly giving the value of BS for each of the sixteen settings of BT, ST, BH, and SH. This is just a long-winded way of saying that I allow (but do not require) models to be described succinctly. Moreover, the description is such that it is easy to determine (i.e., in time polynomial in the description of the model), for each context
for the rock-throwing example is given as BS = BH ∨ SH, rather than explicitly giving the value of BS for each of the sixteen settings of BT, ST, BH, and SH. This is just a long-winded way of saying that I allow (but do not require) models to be described succinctly. Moreover, the description is such that it is easy to determine (i.e., in time polynomial in the description of the model), for each context ![[image]](images/eqn642.jpg) , the unique solution to the equations. Listing the equations in the “affects” order determined by
, the unique solution to the equations. Listing the equations in the “affects” order determined by ![[image]](images/eqn643.jpg) can help in this task; the value of each endogenous variable can then be determined in sequence.
can help in this task; the value of each endogenous variable can then be determined in sequence.
With this background, I can state the relevant complexity results.
Theorem 5.3.1
(a) The complexity of determining whether ![[image]](images/eqn644.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dclimg0140.jpg) under the original HP definition is
under the original HP definition is ![[image]](images/eqn645.jpg) .
.
(b) The complexity of determining whether ![[image]](images/eqn646.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dclimg0141.jpg) under the updated HP definition is
under the updated HP definition is ![[image]](images/eqn647.jpg) .
.
(c) The complexity of determining whether ![[image]](images/eqn648.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dclimg0142.jpg) under the modified HP definition is
under the modified HP definition is ![[image]](images/eqn649.jpg) .
.
The proofs of parts (a) and (b) of Theorem 5.3.1 are beyond the scope of this book (see the notes at the end of the chapter for references); the proof of part (c) can be found in Section 5.5.2.
These results seem somewhat disconcerting. Even ![[image]](images/eqn650.jpg) is considered intractable, which suggests that it may be hard to determine whether
is considered intractable, which suggests that it may be hard to determine whether ![[image]](images/eqn651.jpg) is a cause of φ in general. There are some reasons to believe that the situation is not quite so bad. First, in practice, there may be quite a bit of structure in causal models that may make the computation much simpler. The kinds of models that we use to get the hardness results are not typical. Second, there are two important special cases that are not so complicated, as the following result shows.
is a cause of φ in general. There are some reasons to believe that the situation is not quite so bad. First, in practice, there may be quite a bit of structure in causal models that may make the computation much simpler. The kinds of models that we use to get the hardness results are not typical. Second, there are two important special cases that are not so complicated, as the following result shows.
Theorem 5.3.2
(a) The complexity of determining whether X = x is a cause of φ in ![[image]](images/dclimg0143.jpg) under the original HP definition is NP-complete in binary models (i.e., models where all variables are binary).
under the original HP definition is NP-complete in binary models (i.e., models where all variables are binary).
(b) The complexity of determining whether X = x is a cause of φ in ![[image]](images/dclimg0144.jpg) under the modified HP definition is NP-complete.
under the modified HP definition is NP-complete.
As we have observed, the restriction to singleton causes is made without loss of generality for the original HP definition. Although the restriction to binary models does entail some loss of generality, binary models do arise frequently in practice; indeed, almost all the examples in this book have involved binary models. The restriction to singleton causes does entail a nontrivial loss of generality for the modified HP definition. As we have seen, in voting scenarios and in the disjunctive case of the forest-fire example, causes are not singletons. Nevertheless, many examples of interest do involve singleton causes.
This may not seem like major progress. Historically, even NP-complete problems were considered intractable. However, recently, major advances have been made in finding algorithms that deal well with many NP-complete problems; there seems to be some hope on this front.
5.4 Axiomatizing Causal Reasoning
The goal of this section is to understand the properties of causality in greater detail. The technique that I use for doing so is to characterize causal reasoning axiomatically. Before doing this, I first review some standard definitions from logic.
An axiom system AX consists of a collection of axioms and inference rules. An axiom is a formula (in some predetermined language ![[image]](images/eqn652.jpg) ), and an inference rule has the form “from φ1,…, φk infer ψ,” where φ1,…, φk, ψ are formulas in
), and an inference rule has the form “from φ1,…, φk infer ψ,” where φ1,…, φk, ψ are formulas in ![[image]](images/eqn653.jpg) . A proof in AX consists of a sequence of formulas in
. A proof in AX consists of a sequence of formulas in ![[image]](images/eqn654.jpg) , each of which is either an axiom in AX or follows by an application of an inference rule. A proof is said to be a proof of the formula φ if the last formula in the proof is φ. The formula φ is said to be provable in AX, written AX ⊢ φ, if there is a proof of φ in AX; similarly, φ is said to be consistent with AX if ¬φ is not provable in AX.
, each of which is either an axiom in AX or follows by an application of an inference rule. A proof is said to be a proof of the formula φ if the last formula in the proof is φ. The formula φ is said to be provable in AX, written AX ⊢ φ, if there is a proof of φ in AX; similarly, φ is said to be consistent with AX if ¬φ is not provable in AX.
A formula φ is valid in causal structure M, written M ⊨ φ, if (M, ![[image]](images/eqn655.jpg) ) ⊨ φ in all contexts
) ⊨ φ in all contexts ![[image]](images/eqn656.jpg) . The formula φ is valid in a set
. The formula φ is valid in a set ![[image]](images/eqn657.jpg) of causal structures if M ⊨ φ for all
of causal structures if M ⊨ φ for all ![[image]](images/eqn658.jpg) ; φ is satisfiable in
; φ is satisfiable in ![[image]](images/eqn659.jpg) if there is a causal structure
if there is a causal structure ![[image]](images/eqn660.jpg) and a context
and a context ![[image]](images/eqn661.jpg) such that (M,
such that (M, ![[image]](images/eqn662.jpg) ) ⊨ φ. Note that φ is valid in
) ⊨ φ. Note that φ is valid in ![[image]](images/eqn663.jpg) iff ¬φ is not satisfiable in
iff ¬φ is not satisfiable in ![[image]](images/eqn664.jpg) .
.
The notions of soundness and completeness connect provability and validity. An axiom system AX is said to be sound for a language ![[image]](images/eqn665.jpg) with respect to a set
with respect to a set ![[image]](images/eqn666.jpg) of causal models if every formula in
of causal models if every formula in ![[image]](images/eqn667.jpg) provable in AX is valid with respect to
provable in AX is valid with respect to ![[image]](images/eqn668.jpg) . AX is complete for
. AX is complete for ![[image]](images/eqn669.jpg) with respect to
with respect to ![[image]](images/eqn670.jpg) if every formula in
if every formula in ![[image]](images/eqn671.jpg) that is valid with respect to
that is valid with respect to ![[image]](images/eqn672.jpg) is provable in AX.
is provable in AX.
The causal models and language that I consider here are parameterized by a signature ![[image]](images/eqn673.jpg) . (Recall that
. (Recall that ![[image]](images/eqn674.jpg) is the set of exogenous variables,
is the set of exogenous variables, ![[image]](images/eqn675.jpg) is the set of endogenous variables, and for each variable Y,
is the set of endogenous variables, and for each variable Y, ![[image]](images/eqn676.jpg) is the range of Y.) I restrict
is the range of Y.) I restrict ![[image]](images/eqn677.jpg) here to signatures where
here to signatures where ![[image]](images/eqn678.jpg) is finite and the range of each endogenous variable is finite. This restriction certainly holds in all the examples that I consider in this book. For each signature
is finite and the range of each endogenous variable is finite. This restriction certainly holds in all the examples that I consider in this book. For each signature ![[image]](images/eqn679.jpg) , I consider
, I consider ![[image]](images/eqn680.jpg) , the set of all recursive causal models with signature
, the set of all recursive causal models with signature ![[image]](images/eqn681.jpg) . The language that I consider is
. The language that I consider is ![[image]](images/eqn682.jpg) , the language of causal formulas defined in Section 2.2.1, where the variables are restricted to those in
, the language of causal formulas defined in Section 2.2.1, where the variables are restricted to those in ![[image]](images/eqn683.jpg) , and the range of these variables is given by
, and the range of these variables is given by ![[image]](images/eqn684.jpg) .
. ![[image]](images/eqn685.jpg) is rich enough to express actual causality in models in
is rich enough to express actual causality in models in ![[image]](images/eqn686.jpg) . More precisely, given
. More precisely, given ![[image]](images/eqn687.jpg) ,
, ![[image]](images/eqn688.jpg) , φ, and,
, φ, and, ![[image]](images/eqn689.jpg) for each variant of the HP definition, it is straightforward to construct a formula ψ in this language such that (M,
for each variant of the HP definition, it is straightforward to construct a formula ψ in this language such that (M, ![[image]](images/eqn690.jpg) ) ⊨ ψ for a causal model
) ⊨ ψ for a causal model ![[image]](images/eqn691.jpg) if and only if
if and only if ![[image]](images/eqn692.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/dclimg0145.jpg) . (The existential quantification implicit in the statement of AC2(a) and AC2(am) can be expressed using a disjunction because the set
. (The existential quantification implicit in the statement of AC2(a) and AC2(am) can be expressed using a disjunction because the set ![[image]](images/eqn693.jpg) of endogenous variables is assumed to be finite; similarly, the universal quantification implicit in the statement of AC2(bo) and AC2(bu) can be expressed using a conjunction.) Moreover, the language can express features of models, such as the effect of interventions. Thus, we will be able to see what inferences can be made if we understand the effect of various interventions. For example, results like Propositions 2.4.3 and 2.4.4 that provide sufficient conditions for causality to be transitive follow from the axioms.
of endogenous variables is assumed to be finite; similarly, the universal quantification implicit in the statement of AC2(bo) and AC2(bu) can be expressed using a conjunction.) Moreover, the language can express features of models, such as the effect of interventions. Thus, we will be able to see what inferences can be made if we understand the effect of various interventions. For example, results like Propositions 2.4.3 and 2.4.4 that provide sufficient conditions for causality to be transitive follow from the axioms.
To help characterize causal reasoning in ![[image]](images/eqn694.jpg) , where
, where ![[image]](images/eqn695.jpg) , it is helpful to define a formula Y ⤳ Z for Y,
, it is helpful to define a formula Y ⤳ Z for Y, ![[image]](images/eqn696.jpg) , read “Y affects Z”. Intuitively, this formula is true in a model M and context
, read “Y affects Z”. Intuitively, this formula is true in a model M and context ![[image]](images/eqn697.jpg) if there is a setting of the variables other than Y and Z such that changing the value of Y changes the value of Z. Formally, taking
if there is a setting of the variables other than Y and Z such that changing the value of Y changes the value of Z. Formally, taking ![[image]](images/eqn698.jpg) (so that
(so that ![[image]](images/eqn699.jpg) consists of the endogenous variables other than Y and Z), and taking
consists of the endogenous variables other than Y and Z), and taking ![[image]](images/eqn700.jpg) to be the range of the variables in
to be the range of the variables in ![[image]](images/eqn701.jpg) , Y ⤳ Z is an abbreviation of
, Y ⤳ Z is an abbreviation of
![[image]](images/eqn702.jpg)
which is a formula in ![[image]](images/eqn703.jpg) . (In statisticians’ notation, this says that Y ⤳ Z is true in a context
. (In statisticians’ notation, this says that Y ⤳ Z is true in a context ![[image]](images/eqn704.jpg) if there exists y, y′, z, and z′ with z ≠ z′ such that
if there exists y, y′, z, and z′ with z ≠ z′ such that ![[image]](images/eqn705.jpg) The disjunction is really acting as an existential quantifier here; this is one place I am using the fact that the range of each endogenous variable is finite. (With existential quantification in the language, I would not need this assumption.)
The disjunction is really acting as an existential quantifier here; this is one place I am using the fact that the range of each endogenous variable is finite. (With existential quantification in the language, I would not need this assumption.)
Consider the following axioms C0–5 and rule of inference MP. (I translate the first four axioms into statisticians’ notation, omitting the context ![[image]](images/eqn706.jpg) since they are intended to hold for all contexts
since they are intended to hold for all contexts ![[image]](images/eqn707.jpg) . The representation in this case is quite compact. However, standard statisticians’ notation is not so well suited for translating axiom C6, although of course it could be extended to capture it.)
. The representation in this case is quite compact. However, standard statisticians’ notation is not so well suited for translating axiom C6, although of course it could be extended to capture it.)
![[image]](images/eqn708.jpg)
To explain the notion of substitution instance in C0, note that, for example, p ∨ ¬p is a propositional tautology; ![[image]](images/eqn716.jpg) (i.e.,
(i.e., ![[image]](images/eqn717.jpg) ) is a substitution instance of it, obtained by substituting
) is a substitution instance of it, obtained by substituting ![[image]](images/eqn718.jpg) for p. More generally, by a substitution instance of a propositional tautology φ, I mean the result of uniformly replacing all primitive propositions in φ by arbitrary formulas of
for p. More generally, by a substitution instance of a propositional tautology φ, I mean the result of uniformly replacing all primitive propositions in φ by arbitrary formulas of ![[image]](images/eqn719.jpg) . C1 just states an obvious property of equality: if X = x in the unique solution of the equations in context
. C1 just states an obvious property of equality: if X = x in the unique solution of the equations in context ![[image]](images/eqn720.jpg) of model
of model ![[image]](images/eqn721.jpg) , then we cannot have X = x′ if x′ ≠ x. C2 states that there is some value
, then we cannot have X = x′ if x′ ≠ x. C2 states that there is some value ![[image]](images/eqn722.jpg) that is the value of X in all solutions to the equations in context
that is the value of X in all solutions to the equations in context ![[image]](images/eqn723.jpg) in
in ![[image]](images/eqn724.jpg) . Note that the statement of C2 makes use of the fact that
. Note that the statement of C2 makes use of the fact that ![[image]](images/eqn725.jpg) is finite (for otherwise C2 would involve an infinite disjunction). C3 says that if, after setting
is finite (for otherwise C2 would involve an infinite disjunction). C3 says that if, after setting ![[image]](images/eqn726.jpg) to
to ![[image]](images/eqn727.jpg) , Y = y and W = w, then W = w if we both set
, Y = y and W = w, then W = w if we both set ![[image]](images/eqn728.jpg) to
to ![[image]](images/eqn729.jpg) and Y to y; this was proved in Lemma 2.10.2. C4 simply says that in all solutions obtained after setting X to x, the value of X is x. It is easy to see that C5 holds in recursive models. For if
and Y to y; this was proved in Lemma 2.10.2. C4 simply says that in all solutions obtained after setting X to x, the value of X is x. It is easy to see that C5 holds in recursive models. For if ![[image]](images/eqn730.jpg) , then
, then ![[image]](images/eqn731.jpg) . Thus, if
. Thus, if ![[image]](images/eqn732.jpg) , then
, then ![[image]](images/eqn733.jpg) , so we cannot have
, so we cannot have ![[image]](images/eqn734.jpg) if X0 ≠ Xk. Thus,
if X0 ≠ Xk. Thus, ![[image]](images/eqn735.jpg) . Finally, the validity of C6 is almost immediate from the semantics of the relevant formulas.
. Finally, the validity of C6 is almost immediate from the semantics of the relevant formulas.
C5 can be viewed as a collection of axioms (actually, axiom schemes), one for each k. The case k = 1 already gives us ¬(Y ⤳ Z) ∨¬ (Z ⤳ Y) for all distinct variables Y and Z. That is, it tells us that, for any pair of variables, at most one affects the other. However, it can be shown that just restricting C5 to the case of k = 1 does not suffice to characterize ![[image]](images/eqn736.jpg) .
.
Let ![[image]](images/eqn737.jpg) consist of C0–C6 and MP.
consist of C0–C6 and MP. ![[image]](images/eqn738.jpg) characterizes causal reasoning in recursive models, as the following theorem shows.
characterizes causal reasoning in recursive models, as the following theorem shows.
Theorem 5.4.1 ![[image]](images/eqn739.jpg) is a sound and complete axiomatization for the language
is a sound and complete axiomatization for the language ![[image]](images/eqn740.jpg) in
in ![[image]](images/eqn741.jpg) .
.
Proof: See Section 5.5.3. ■
We can also consider the complexity of determining whether a formula φ is valid in ![[image]](images/eqn742.jpg) (or, equivalently, is provable in
(or, equivalently, is provable in ![[image]](images/eqn743.jpg) . This depends in part on how we formulate the problem.
. This depends in part on how we formulate the problem.
One version of the problem is to consider a fixed signature ![[image]](images/eqn744.jpg) and ask how hard it is to decide whether a formula
and ask how hard it is to decide whether a formula ![[image]](images/eqn745.jpg) is valid. This turns out to be quite easy, for trivial reasons.
is valid. This turns out to be quite easy, for trivial reasons.
Theorem 5.4.2 If ![[image]](images/eqn746.jpg) is a fixed finite signature, the problem of deciding if a formula
is a fixed finite signature, the problem of deciding if a formula ![[image]](images/eqn747.jpg) is valid in
is valid in ![[image]](images/eqn748.jpg) can be solved in time linear in |φ| (the length of φ viewed as a string of symbols).
can be solved in time linear in |φ| (the length of φ viewed as a string of symbols).
Proof: If ![[image]](images/eqn749.jpg) is finite, there are only finitely many causal models in
is finite, there are only finitely many causal models in ![[image]](images/eqn750.jpg) , independent of φ. Given φ, we can explicitly check whether φ is valid in any (or all) of them. This can be done in time linear in |φ|. Since
, independent of φ. Given φ, we can explicitly check whether φ is valid in any (or all) of them. This can be done in time linear in |φ|. Since ![[image]](images/eqn751.jpg) is not a parameter to the problem, the huge number of possible causal models that we have to check affects only the constant. ■
is not a parameter to the problem, the huge number of possible causal models that we have to check affects only the constant. ■
We can do even better than Theorem 5.4.2 suggests. Suppose that ![[image]](images/eqn752.jpg) consists of 100 variables and φ mentions only 3 of them. A causal model must specify the equations for all 100 variables. Is it really necessary to consider what happens to the 97 variables not mentioned in φ to decide whether φ is satisfiable or valid? As the following result shows, we need to check only the variables that appear in φ. Given a signature
consists of 100 variables and φ mentions only 3 of them. A causal model must specify the equations for all 100 variables. Is it really necessary to consider what happens to the 97 variables not mentioned in φ to decide whether φ is satisfiable or valid? As the following result shows, we need to check only the variables that appear in φ. Given a signature ![[image]](images/eqn753.jpg) and a context
and a context ![[image]](images/eqn754.jpg) , where
, where ![[image]](images/eqn755.jpg) consists of the variables in
consists of the variables in ![[image]](images/eqn756.jpg) that appear in φ,
that appear in φ, ![[image]](images/eqn757.jpg) , and
, and ![[image]](images/eqn758.jpg) for all variables
for all variables ![[image]](images/eqn759.jpg) .
.
Theorem 5.4.3 A formula ![[image]](images/eqn760.jpg) is satisfiable in
is satisfiable in ![[image]](images/eqn761.jpg) iff there exists
iff there exists ![[image]](images/eqn762.jpg) such that φ is satisfiable in
such that φ is satisfiable in ![[image]](images/eqn763.jpg) .
.
Proof: See Section 5.5.3. ■
Theorem 5.4.2 is the analogue of the observation that for propositional logic, the satisfiability problem is in linear time if we restrict to a fixed set of primitive propositions. The proof that the satisfiability problem for propositional logic is NP-complete implicitly assumes that we have an unbounded number of primitive propositions at our disposal. There are two ways to get an analogous result here. The first is to allow the signature ![[image]](images/eqn764.jpg) to be infinite; the second is to make the signature part of the input to the problem. The results in both cases are similar, so I just consider the case where the signature is part of the input here.
to be infinite; the second is to make the signature part of the input to the problem. The results in both cases are similar, so I just consider the case where the signature is part of the input here.
Theorem 5.4.4 Given as input a pair (φ, ![[image]](images/eqn765.jpg) ), where
), where ![[image]](images/eqn766.jpg) and
and ![[image]](images/eqn767.jpg) is a finite signature, the problem of deciding if φ is satisfiable in
is a finite signature, the problem of deciding if φ is satisfiable in ![[image]](images/eqn768.jpg) is NP-complete.
is NP-complete.
Proof: See Section 5.5.3. ■
Thus, the satisfiability problem for the language of causality is no harder than it is for propositional logic. Since satisfiability is the dual of validity, the same is true for the validity problem (which is co-NP-complete). This can be viewed as good news. The techniques developed to test for satisfiability of propositional formulas can perhaps be applied to testing the satisfiability of causal formulas as well.
5.5 Technical Details and Proofs
In this section, I go through some of the technical details that I deferred earlier.
5.5.1 Algebraic plausibility measures: the details
In this section, I fill in the technical details of the construction of algebraic plausibility measures. I start with the formal definition.
Definition 5.5.1 An algebraic conditional plausibility measure (algebraic cpm) Pl on W maps pairs of subsets of W to a domain D that is endowed with operations ⊕ and ⊗, defined on domains Dom(⊕) and Dom(⊗), respectively, such that the following properties hold:
Alg1. If U1 and U2 are disjoint subsets of W and V ≠ ∅, then
![[image]](images/eqn769.jpg)
Alg2. If U ⊆ V ⊆ V′ and V ≠ ∅, then Pl(U | V′) = Pl(U | V) ⊗ Pl(V | V′).
Alg3. ⊗ distributes over ⊕; more precisely, a ⊗ (b1 ⊕⋯⊕ bn) = (a ⊗ b1) ⊕⋯⊕ (a ⊗ bn) if (a, b1),…, (a, bn), (a, b1⊕⋯⊕bn) ∈ Dom(⊗) and (b1,…, bn), (a⊗b1,…, a⊗bn) ∈ Dom(⊕), where Dom(⊕) = {(Pl(U1 | V),…, Pl(Un | V)): U1,…, Un are pairwise disjoint and V ≠ ∅} and Dom(⊗) = {(Pl(U | V), Pl(V | V′)): U ⊆ V ⊆ V′, V ≠ ∅}. (The reason that this property is required only for tuples in Dom(⊕) and Dom(⊗) is discussed shortly. Note that parentheses are not required in the expression b1 ⊕⋯⊕ bn although, in general, ⊕ need not be associative. This is because it follows immediately from Alg1 that ⊕ is associative and commutative on tuples in Dom(⊕).)
Alg4. If (a, c), (b, c) ∈ Dom(⊗), a ⊗ c ≤ b ⊗ c, and c ≠ ⊥, then a ≤ b. ■
The restrictions in Alg3 and Alg4 to tuples in Dom(⊕) and Dom(⊗) make these conditions a little more awkward to state. It may seem more natural to consider a stronger version of, say, Alg4 that applies to all pairs in D × D. Requiring Alg3 and Alg4 to hold only for limited domains allows the notion of an algebraic plausibility measure to apply to a (usefully) larger set of plausibility measures.
Roughly speaking, Dom(⊕) and Dom(⊗) are the only sets where we really care how ⊕ and ⊗ work. We use ⊕ to determine the (conditional) plausibility of the union of two disjoint sets. Thus, we care about a ⊕ b only if a and b have the form Pl(U1 | V) and Pl(U2 | V), respectively, where U1 and U2 are disjoint sets, in which case we want a ⊕ b to be Pl(U1 ∪ U2 | V). More generally, we care about a1⊕⋯⊕an only if ai has the form Pl(Ui | V), where U1,…, Un are pairwise disjoint. Dom(⊕) consists of precisely these tuples of plausibility values. Similarly, we care about a ⊗ b only if a and b have the form Pl(U |V) and Pl(V |V′), respectively, where U ⊆ V ⊆ V′, in which case we want a ⊗ b to be Pl(U |V). Dom(⊗) consists of precisely these pairs (a, b). Restricting ⊕ and ⊗ to Dom(⊕) and Dom(⊗) will make it easier for us to view a partial preorder as an algebraic plausibility measure. Since ⊕ and ⊗ are significant mainly to the extent that Alg1 and Alg2 hold, and Alg1 and Alg2 apply to tuples in Dom(⊕) and Dom(⊗), respectively, it does not seem unreasonable that properties like Alg3 and Alg4 be required to hold only for these tuples.
In an algebraic cpm, we can define a set U to be plausibilistically independent of V conditional on V′ if V ∩ V′ ≠ ∅ implies that Pl(U | V ∩ V′) = Pl(U | V′). The intuition here is that learning V does not affect the conditional plausibility of U given V′. Note that conditional independence is, in general, asymmetric. U can be conditionally independent of V without V being conditionally independent of U. Although this may not look like the standard definition of probabilistic conditional independence, it is not hard to show that this definition agrees with the standard definition (that Pr(U ∩ V | V′) = Pr(U | V′) × Pr(V | V′)) in the special case that the plausibility measure is actually a probability measure, provided that Pr(V ∩ V′) ≠ 0. Of course, in this case, the definition is symmetric.
The next step is to show how to represent a partial preorder on worlds as an algebraic plausibility measure. Given an extended causal model ![[image]](images/eqn770.jpg) , define a preorder ⪰e on subsets of W just as in Section 3.5: U ⪰e V if, for all w ∈ V, there exists some w′ ∈ U such that w′ ⪰ w. Recall that ⪰e extends the partial preorder ⪰ on worlds. We might consider getting an unconditional plausibility measure Pl⪰ that extends the partial preorder on worlds by taking the range of Pl⪰ to be subsets of W, defining Pl⪰ as the identity (i.e., taking Pl⪰(U) = U), and taking U ≥ V iff U ⪰e V.
, define a preorder ⪰e on subsets of W just as in Section 3.5: U ⪰e V if, for all w ∈ V, there exists some w′ ∈ U such that w′ ⪰ w. Recall that ⪰e extends the partial preorder ⪰ on worlds. We might consider getting an unconditional plausibility measure Pl⪰ that extends the partial preorder on worlds by taking the range of Pl⪰ to be subsets of W, defining Pl⪰ as the identity (i.e., taking Pl⪰(U) = U), and taking U ≥ V iff U ⪰e V.
This almosts works. There is a subtle problem though. The relation ≥ used in plausibility measures must be a partial order, not a partial preorder. Recall that for ≥ to be a partial order on a set X, if x ≥ x′ and x′ ≥ x, we must have x′ = x; this is not required for a partial preorder. Thus, for example, if w ⪰ w′ and w′ ⪰ w, then we want Pl⪰({w}) = Pl⪰ ({w′}). This is easily arranged.
Define U ≡ V if U ⪰e V and V ⪰e U. Let [U] = {U′ ⊆ W: U′ ≡ U}; that is, [U] consists of all sets equivalent to U according to ⪰e. We call U the equivalence class of U. Now define Pl⪰(U) = [U], and define an order ≥ on equivalence classes by taking [U] ≥ [V] iff U′ ⪰e V′ for some U′ ∈ [U] and V′ ∈ [V]. It is easy to check that ≥ is well defined on equivalence classes (since if U′ ⪰e V′ for some U′ ∈ [U] and V′ ∈ [V], then U′ ⪰e V′ for all U′ ∈ [U] and V′ ∈ [V]—for all w ∈ V′, there must be some w′ ∈ U′ such that w′ ⪰ w) and is a partial order.
Although this gives us an unconditional plausibility measure extending ⪰, we are not quite there yet. We need a conditional plausibility measure and a definition of ⊕ and ⊗. Note that if U1, U2 ∈ [U], then U1 ∪ U2 ∈ [U]. Since W is finite, it follows that each set [U] has a largest element, namely, the union of the sets in [U].
Let D be the domain consisting of ⊥, ⊤, and all elements of the form d[U]|[V] for all [U] and [V] such that the largest element in [U] is a strict subset of the largest element in [V]. Intuitively, d[U]|[V] represents the plausibility of U conditional on V; the definition given below enforces this intuition. Place an ordering ≥ on D by taking ⊥ < d[U]|[V] < T and d[U]|[V] ≥d[U′]|[V′] if [V] = [V′] and U′ ⪰e U. D can be viewed as the range of an algebraic plausibility measure, defined by taking
![[image]](images/eqn771.jpg)
It remains to define ⊕ and ⊗ on D so that Alg1 and Alg2 hold. This is easy to do, in large part because ⊕ and ⊗ must be defined only on Dom(⊕) and Dom(⊗), where the definitions are immediate because of the need to satisfy Alg1 and Alg2. It is easy to see that these conditions and the definition of Pl guarantee that Pl1–4 hold. With a little more work, it can be shown that these conditions imply Alg3 and Alg4 as well. (Here the fact that Alg3 and Alg4 are restricted to Dom(⊕) and Dom(⊗) turns out to be critical; it is also important that U ≡ V implies that U ≡ U ∪ V.) I leave details to the interested reader.
This construction gives an algebraic cpm, as desired.
5.5.2 Proof of Theorems 5.3.1(c) and 5.3.2(b)
In this section, I prove that the complexity of determining of ![[image]](images/eqn772.jpg) is a cause of φ in
is a cause of φ in ![[image]](images/eqn773.jpg) complete under the modified HP definition. Formally, we want to show that the language
complete under the modified HP definition. Formally, we want to show that the language
![[image]](images/eqn774.jpg)
is ![[image]](images/eqn775.jpg) Let
Let
![[image]](images/eqn776.jpg)
![[image]](images/eqn777.jpg)
Clearly ![[image]](images/eqn778.jpg) .
.
It is easy to see that LAC2 is in NP and LAC3 is in co-NP. Checking that AC1 holds can be done in polynomial time. To check whether AC2(am) holds, we can guess ![[image]](images/eqn779.jpg) and
and ![[image]](images/eqn780.jpg) , and check in polynomial time that
, and check in polynomial time that ![[image]](images/eqn781.jpg) (where
(where ![[image]](images/eqn782.jpg) is such that
is such that ![[image]](images/eqn783.jpg) . Finally, checking whether AC3 is not satisfied can be done by guessing a counterexample and verifying. Since
. Finally, checking whether AC3 is not satisfied can be done by guessing a counterexample and verifying. Since ![[image]](images/eqn784.jpg) , it follows by definition that
, it follows by definition that ![[image]](images/eqn785.jpg) is
is ![[image]](images/eqn786.jpg) .
.
To see that ![[image]](images/eqn787.jpg) is
is ![[image]](images/eqn788.jpg) , first observe that the language Sat × Satc, that is, the language consisting of pairs (ψ, ψ′) of formulas such that ψ is satisfiable and ψ′ is not satisfiable, is
, first observe that the language Sat × Satc, that is, the language consisting of pairs (ψ, ψ′) of formulas such that ψ is satisfiable and ψ′ is not satisfiable, is ![[image]](images/eqn789.jpg) . For if
. For if ![[image]](images/eqn790.jpg) is the set of formulas of propositional logic, then Sat × Satc is the intersection of a language in
is the set of formulas of propositional logic, then Sat × Satc is the intersection of a language in ![[image]](images/eqn791.jpg) and a language in co-NP
and a language in co-NP ![[image]](images/eqn792.jpg) , so it is in
, so it is in ![[image]](images/eqn793.jpg) . To show that Sat × Satc is
. To show that Sat × Satc is ![[image]](images/eqn794.jpg) , suppose that
, suppose that ![[image]](images/eqn795.jpg) is an arbitrary language in
is an arbitrary language in ![[image]](images/eqn796.jpg) . There must exist languages
. There must exist languages ![[image]](images/eqn797.jpg) and
and ![[image]](images/eqn798.jpg) in NP and co-NP, respectively, such that
in NP and co-NP, respectively, such that ![[image]](images/eqn799.jpg) . Since Sat is NP-complete, there must exist a polynomial-time computable function f reducing
. Since Sat is NP-complete, there must exist a polynomial-time computable function f reducing ![[image]](images/eqn800.jpg) to Sat; that is,
to Sat; that is, ![[image]](images/eqn801.jpg) iff f (x) ∈ Sat. Similarly, there must be a polynomial-time function g reducing
iff f (x) ∈ Sat. Similarly, there must be a polynomial-time function g reducing ![[image]](images/eqn802.jpg) to Satc. The function (f, g) mapping x to (f (x), g(x)) gives a polynomial-time reduction from
to Satc. The function (f, g) mapping x to (f (x), g(x)) gives a polynomial-time reduction from ![[image]](images/eqn803.jpg) to Sat × Satc:
to Sat × Satc: ![[image]](images/eqn804.jpg) iff (f (x), g(x)) ∈ Sat × Satc.
iff (f (x), g(x)) ∈ Sat × Satc.
Thus, to show that ![[image]](images/eqn805.jpg) is
is ![[image]](images/eqn806.jpg) , it suffices to reduce Sat×Satc to
, it suffices to reduce Sat×Satc to ![[image]](images/eqn807.jpg) . I now map a pair (ψ, ψ′) of formulas to a tuple (M,
. I now map a pair (ψ, ψ′) of formulas to a tuple (M, ![[image]](images/eqn808.jpg) , Z = 0, (X0, X1), (0, 0)) such that (ψ, ψ′) ∈ Sat × Satc iff X0 = 0 ∧ X1 = 0 is a cause of Z = 0 in
, Z = 0, (X0, X1), (0, 0)) such that (ψ, ψ′) ∈ Sat × Satc iff X0 = 0 ∧ X1 = 0 is a cause of Z = 0 in ![[image]](images/eqn809.jpg) according to the modified HP definition.
according to the modified HP definition.
We can assume without loss of generality that ψ and ψ′ involve disjoint sets of variables (if not, rename all the variables in ψ′ so that they do not appear in ψ; this can clearly be done without affecting whether ψ′ is satisfiable). Suppose that the variables that appear in ψ and ψ′ are included in Y1,…, Yn. Consider the causal model M with endogenous variables X0, X1, Y1,…, Yn, Z, one exogenous variable U, and the following equations:
I claim that (a) if ψ is not satisfiable, then there is no cause of Z = 0 in (M, 0) according to the modified HP definition; (b) if both ψ and ψ′ are satisfiable, then X0 = 0 is a cause of Z = 0 in (M, 0); and (c) if ψ is satisfiable and ψ′ is unsatisfiable, then X0 = 0 ∧ X1 = 0 is a cause of Z = 0 in (M, 0). Clearly, (a) holds; if ψ is unsatisfiable, then no setting of the variables will make Z = 1. For (b), suppose that ψ and ψ′ are both satisfiable. Since ψ and ψ′ involve disjoint sets of variables, there is a truth assignment a to the variables Y1,…, Yn that makes ψ ∧ ψ′ true. Let ![[image]](images/eqn809a.jpg) be the subset of variables in {Y1,…, Yn} that are set to 0 (i.e., false) in a. It follows that
be the subset of variables in {Y1,…, Yn} that are set to 0 (i.e., false) in a. It follows that ![[image]](images/eqn810.jpg) , so
, so ![[image]](images/eqn811.jpg) and AC2(am) holds. AC3 is immediate. Thus, X0 = 0 is indeed a cause of Z = 0, as desired. Finally, for (c), if ψ′ is unsatisfiable, then it is clear that neither X0 = 0 nor X1 = 0 individually is a cause of Z = 0 in (M, 0); to have Z = 1, we must set both X0 = 1 and X1 = 1. Moreover, the same argument as in part (b) shows that, since ψ is satisfiable, we can find a subset
and AC2(am) holds. AC3 is immediate. Thus, X0 = 0 is indeed a cause of Z = 0, as desired. Finally, for (c), if ψ′ is unsatisfiable, then it is clear that neither X0 = 0 nor X1 = 0 individually is a cause of Z = 0 in (M, 0); to have Z = 1, we must set both X0 = 1 and X1 = 1. Moreover, the same argument as in part (b) shows that, since ψ is satisfiable, we can find a subset ![[image]](images/eqn812.jpg) of {Y1,…, Yn} such that
of {Y1,…, Yn} such that ![[image]](images/eqn813.jpg) , so
, so ![[image]](images/eqn814.jpg) . This shows that X0 = 1 ∧ X1 = 1 is a cause of Z = 0 iff (ψ, ψ′) ∈ Sat × Satc. This completes the proof of Theorem 5.3.1(c).
. This shows that X0 = 1 ∧ X1 = 1 is a cause of Z = 0 iff (ψ, ψ′) ∈ Sat × Satc. This completes the proof of Theorem 5.3.1(c).
The proof of Theorem 5.3.2(b) is almost immediate. Now we want to show that the language
![[image]](images/eqn815.jpg)
is NP-complete. AC3 trivially holds and, as we have observed, checking that AC1 and AC2(am) holds is in NP. Moreover, the argument above shows that AC2(am) is NP-hard even if we consider only singleton causes.
5.5.3 Proof of Theorems 5.4.1, 5.4.2, and 5.4.4
In this section, I prove Theorems 5.4.1, 5.4.2, and 5.4.4. I repeat the statements for the reader’s convenience.
Theorem 5.4.1: AXrec(S) is a sound and complete axiomatization for the language ![[image]](images/eqn816.jpg) in
in ![[image]](images/eqn817.jpg) .
.
Proof: The fact that C1, C2, C4, and C6 are valid is almost immediate; the soundness of C3 was proved in Lemma 2.10.2; and the soundness of C5 is discussed in Section 5.4 before the statement of the theorem.
For completeness, it suffices to prove that if a formula φ in ![[image]](images/eqn818.jpg) is consistent with
is consistent with ![[image]](images/eqn819.jpg) (i.e., its negation is not provable), then φ is satisfiable in
(i.e., its negation is not provable), then φ is satisfiable in ![[image]](images/eqn820.jpg) . For suppose that every consistent formula is satisfiable and that φ is valid. If φ is not provable, then ¬φ is consistent. By assumption, this means that ¬φ is satisfiable, contradicting the assumption that φ is valid.
. For suppose that every consistent formula is satisfiable and that φ is valid. If φ is not provable, then ¬φ is consistent. By assumption, this means that ¬φ is satisfiable, contradicting the assumption that φ is valid.
So suppose that a formula ![[image]](images/eqn821.jpg) , with
, with ![[image]](images/eqn822.jpg) , is consistent with
, is consistent with ![[image]](images/eqn823.jpg) . Consider a maximal consistent set C of formulas that includes φ. (A maximal consistent set is a set of formulas whose conjunction is consistent such that any larger set of formulas would be inconsistent.) It follows easily from standard propositional reasoning (i.e., using C0 and MP only) that such a maximal consistent set exists. Moreover, it is well known that a maximal
. Consider a maximal consistent set C of formulas that includes φ. (A maximal consistent set is a set of formulas whose conjunction is consistent such that any larger set of formulas would be inconsistent.) It follows easily from standard propositional reasoning (i.e., using C0 and MP only) that such a maximal consistent set exists. Moreover, it is well known that a maximal ![[image]](images/eqn824.jpg) set C has the following properties:
set C has the following properties:
![[image]](images/eqn825.jpg) , either ψ ∈ C or ¬ψ ∈ C;
, either ψ ∈ C or ¬ψ ∈ C;![[image]](images/eqn826.jpg) is in C.
is in C.(See the notes for references for this standard result.) Moreover, from C1 and C2, it follows that for each variable ![[image]](images/eqn827.jpg) and vector
and vector ![[image]](images/eqn828.jpg) of values for
of values for ![[image]](images/eqn829.jpg) , there exists exactly one element
, there exists exactly one element ![[image]](images/eqn830.jpg) such that
such that ![[image]](images/eqn831.jpg) (i.e., in statisticians’ notation,
(i.e., in statisticians’ notation, ![[image]](images/eqn832.jpg) . I now construct a causal model
. I now construct a causal model ![[image]](images/eqn833.jpg) and context
and context ![[image]](images/eqn834.jpg) such that
such that ![[image]](images/eqn835.jpg) ⊨ ψ for every formula ψ ∈ C (and, in particular, φ).
⊨ ψ for every formula ψ ∈ C (and, in particular, φ).
The idea is straightforward: the formulas in C determine ![[image]](images/eqn836.jpg) . For each variable
. For each variable ![[image]](images/eqn837.jpg) , let
, let ![[image]](images/eqn838.jpg) . By C1 and C2, for all
. By C1 and C2, for all ![[image]](images/eqn839.jpg) , there is a unique
, there is a unique ![[image]](images/eqn840.jpg) such that
such that ![[image]](images/eqn841.jpg) . For all contexts
. For all contexts ![[image]](images/eqn842.jpg) , define
, define ![[image]](images/eqn843.jpg) . (Note that FX is independent of the context
. (Note that FX is independent of the context ![[image]](images/eqn844.jpg) .) This defines FX for all endogenous variables X, and hence
.) This defines FX for all endogenous variables X, and hence ![[image]](images/eqn845.jpg) . Let
. Let ![[image]](images/eqn846.jpg) .
.
I claim that for all formulas ![[image]](images/eqn847.jpg) , we have ψ ∈ C iff
, we have ψ ∈ C iff ![[image]](images/eqn848.jpg) for all contexts
for all contexts ![[image]](images/eqn849.jpg) . Before proving this, I need to deal with a subtle issue. The definition of ⊨ was given in Section 2.2.1 under the assumption that M is recursive (i.e.,
. Before proving this, I need to deal with a subtle issue. The definition of ⊨ was given in Section 2.2.1 under the assumption that M is recursive (i.e., ![[image]](images/eqn850.jpg) ). Although I will show this, I have not done so yet. Thus, for now, I take
). Although I will show this, I have not done so yet. Thus, for now, I take ![[image]](images/eqn851.jpg) to hold if there is a unique solution to the equations in the model
to hold if there is a unique solution to the equations in the model ![[image]](images/eqn852.jpg) in context
in context ![[image]](images/eqn853.jpg) , and ψ holds in that solution. This definition is consistent with the definition given in Section 2.2.1 and makes sense even if
, and ψ holds in that solution. This definition is consistent with the definition given in Section 2.2.1 and makes sense even if ![[image]](images/eqn854.jpg) . (Recall that, in Section 2.7, I gave a definition of ⊨ that works even in nonrecursive models. I could have worked with that definition here; it is slightly easier to prove the result using the approach that I have taken.)
. (Recall that, in Section 2.7, I gave a definition of ⊨ that works even in nonrecursive models. I could have worked with that definition here; it is slightly easier to prove the result using the approach that I have taken.)
I first prove that ![[image]](images/eqn855.jpg) for formulas ψ of the form
for formulas ψ of the form ![[image]](images/eqn856.jpg) . The proof is by induction on
. The proof is by induction on ![[image]](images/eqn857.jpg) . First consider the case where
. First consider the case where ![[image]](images/eqn858.jpg) . In that case,
. In that case, ![[image]](images/eqn859.jpg) . If
. If ![[image]](images/eqn860.jpg) , then the value of each endogenous variable is determined by its setting in
, then the value of each endogenous variable is determined by its setting in ![[image]](images/eqn861.jpg) , so there is clearly a unique solution to the equations in
, so there is clearly a unique solution to the equations in ![[image]](images/eqn862.jpg) for every context
for every context ![[image]](images/eqn863.jpg) and X = x in that solution. Conversely, if
and X = x in that solution. Conversely, if ![[image]](images/eqn864.jpg) , then
, then ![[image]](images/eqn865.jpg) is an instance of C4, so must be in C.
is an instance of C4, so must be in C.
If ![[image]](images/eqn866.jpg) and
and ![[image]](images/eqn867.jpg) , then again there is a unique solution to the equations in
, then again there is a unique solution to the equations in ![[image]](images/eqn868.jpg) for each context; the value of each variable
for each context; the value of each variable ![[image]](images/eqn869.jpg) is determined by
is determined by ![[image]](images/eqn870.jpg) , and the value of the one endogenous variable W not in
, and the value of the one endogenous variable W not in ![[image]](images/eqn871.jpg) is determined by the equation FW. If
is determined by the equation FW. If ![[image]](images/eqn872.jpg) and
and ![[image]](images/eqn873.jpg) , then the fact that X = x in the unique solution follows from C4, while if
, then the fact that X = x in the unique solution follows from C4, while if ![[image]](images/eqn874.jpg) , the result follows from the definition of FX. Conversely, if
, the result follows from the definition of FX. Conversely, if ![[image]](images/eqn875.jpg) and
and ![[image]](images/eqn876.jpg) then again
then again ![[image]](images/eqn877.jpg) must be an instance of C4, so must be in C, while if
must be an instance of C4, so must be in C, while if ![[image]](images/eqn878.jpg) , then we must have
, then we must have ![[image]](images/eqn879.jpg) , given how FX is defined.
, given how FX is defined.
For the general case, suppose that ![[image]](images/eqn880.jpg) and
and ![[image]](images/eqn881.jpg) . I want to show that there is a unique solution to the equations in
. I want to show that there is a unique solution to the equations in ![[image]](images/eqn882.jpg) in every context
in every context ![[image]](images/eqn883.jpg) and that in this solution, X has value x. To show that there is a solution, I define a vector
and that in this solution, X has value x. To show that there is a solution, I define a vector ![[image]](images/eqn884.jpg) and show that it is in fact a solution. If
and show that it is in fact a solution. If ![[image]](images/eqn885.jpg) and W ← w is a conjunct of
and W ← w is a conjunct of ![[image]](images/eqn886.jpg) , then set the W component of
, then set the W component of ![[image]](images/eqn887.jpg) to w. If W is not in
to w. If W is not in ![[image]](images/eqn888.jpg) , then set the W component of
, then set the W component of ![[image]](images/eqn889.jpg) to the unique value w such that
to the unique value w such that ![[image]](images/eqn890.jpg) . (By C1 and C2 there is such a unique value w.) I claim that
. (By C1 and C2 there is such a unique value w.) I claim that ![[image]](images/eqn891.jpg) is a solution to the equations in
is a solution to the equations in ![[image]](images/eqn892.jpg) for all contexts
for all contexts ![[image]](images/eqn893.jpg) .
.
To see this, let V1 be a variable in ![[image]](images/eqn894.jpg) , let V2 be an arbitrary variable in
, let V2 be an arbitrary variable in ![[image]](images/eqn895.jpg) , and let v1 and v2 be the values of these variables in
, and let v1 and v2 be the values of these variables in ![[image]](images/eqn896.jpg) . By assumption,
. By assumption, ![[image]](images/eqn897.jpg) ,
, ![[image]](images/eqn898.jpg) , and C contains every instance of C3, so it follows that
, and C contains every instance of C3, so it follows that ![[image]](images/eqn899.jpg) . Since V2 was arbitrary, it follows from the induction hypothesis that
. Since V2 was arbitrary, it follows from the induction hypothesis that ![[image]](images/eqn900.jpg) is the unique solution to the equations in
is the unique solution to the equations in ![[image]](images/eqn901.jpg) for all contexts
for all contexts ![[image]](images/eqn902.jpg) . For every endogenous variable Z other than V1, the equation FZ for Z is the same in
. For every endogenous variable Z other than V1, the equation FZ for Z is the same in ![[image]](images/eqn903.jpg) and in
and in ![[image]](images/eqn904.jpg) . Thus, every equation except possibly that for V1 is satisfied by
. Thus, every equation except possibly that for V1 is satisfied by ![[image]](images/eqn905.jpg) in
in ![[image]](images/eqn906.jpg) for all contexts
for all contexts ![[image]](images/eqn907.jpg) . Since
. Since ![[image]](images/eqn908.jpg) , we can repeat this argument starting with a variable in
, we can repeat this argument starting with a variable in ![[image]](images/eqn909.jpg) other than V1 to conclude that, in fact, every equation in
other than V1 to conclude that, in fact, every equation in ![[image]](images/eqn910.jpg) is satisfied by
is satisfied by ![[image]](images/eqn911.jpg) for all contexts
for all contexts ![[image]](images/eqn912.jpg) . That is,
. That is, ![[image]](images/eqn913.jpg) is a solution to the equations in
is a solution to the equations in ![[image]](images/eqn914.jpg) for all contexts
for all contexts ![[image]](images/eqn915.jpg) .
.
It remains to show that ![[image]](images/eqn916.jpg) is the unique solution to the equations in
is the unique solution to the equations in ![[image]](images/eqn917.jpg) for all contexts
for all contexts ![[image]](images/eqn918.jpg) . Suppose there were another solution, say
. Suppose there were another solution, say ![[image]](images/eqn919.jpg) , to the equations in
, to the equations in ![[image]](images/eqn920.jpg) for some context
for some context ![[image]](images/eqn921.jpg) . There must be some variable V1 whose value in
. There must be some variable V1 whose value in ![[image]](images/eqn922.jpg) is different from its value in
is different from its value in ![[image]](images/eqn923.jpg) . Suppose that the value of V1 in
. Suppose that the value of V1 in ![[image]](images/eqn924.jpg) is v1 and its value in
is v1 and its value in ![[image]](images/eqn925.jpg) is
is ![[image]](images/eqn926.jpg) , with
, with ![[image]](images/eqn927.jpg) . By construction,
. By construction, ![[image]](images/eqn928.jpg) . By C1,
. By C1, ![[image]](images/eqn929.jpg) . Since
. Since ![[image]](images/eqn930.jpg) is a solution to the equations in
is a solution to the equations in ![[image]](images/eqn931.jpg) in context
in context ![[image]](images/eqn932.jpg) , it is easy to check that
, it is easy to check that ![[image]](images/eqn933.jpg) is also a solution to the equations in
is also a solution to the equations in ![[image]](images/eqn934.jpg) in context
in context ![[image]](images/eqn935.jpg) . By the induction hypothesis,
. By the induction hypothesis, ![[image]](images/eqn936.jpg) is the unique solution to the equations in
is the unique solution to the equations in ![[image]](images/eqn937.jpg) in every context. Let V2 be a variable other than V1 in
in every context. Let V2 be a variable other than V1 in ![[image]](images/eqn938.jpg) , and let
, and let ![[image]](images/eqn939.jpg) be the value of V2 in
be the value of V2 in ![[image]](images/eqn940.jpg) . As above,
. As above, ![[image]](images/eqn941.jpg) is the unique solution to the equations in
is the unique solution to the equations in ![[image]](images/eqn942.jpg) in all contexts. It follows from the induction hypothesis that
in all contexts. It follows from the induction hypothesis that ![[image]](images/eqn943.jpg) and
and ![[image]](images/eqn944.jpg) are both in C. I now claim that
are both in C. I now claim that ![[image]](images/eqn945.jpg) . This, together with the fact that
. This, together with the fact that ![[image]](images/eqn946.jpg) (and hence
(and hence ![[image]](images/eqn947.jpg) by C6(a)), contradicts the consistency of C.
by C6(a)), contradicts the consistency of C.
To prove that ![[image]](images/eqn948.jpg) , note that by C5, at most one of V1 ⤳ V2 and V2 ⤳ V1 is in C. If V2 ⤳ V1 ∉ C, then ¬(V2 ⤳ V1) ∈ C, so V2 does not affect V1. Since
, note that by C5, at most one of V1 ⤳ V2 and V2 ⤳ V1 is in C. If V2 ⤳ V1 ∉ C, then ¬(V2 ⤳ V1) ∈ C, so V2 does not affect V1. Since ![[image]](images/eqn949.jpg) , it follows that
, it follows that ![[image]](images/eqn950.jpg) , proving the claim.
, proving the claim.
Now suppose that V1 ⤳ V2 ∉ C. Then an argument analogous to that above shows that ![[image]](images/eqn951.jpg) . If
. If ![[image]](images/eqn952.jpg) , by C2,
, by C2, ![[image]](images/eqn953.jpg) for some
for some ![[image]](images/eqn954.jpg) . Now applying C3, it follows that
. Now applying C3, it follows that ![[image]](images/eqn955.jpg) . But this, together with the fact that
. But this, together with the fact that ![[image]](images/eqn956.jpg) and C1, contradicts the consistency of C. This completes the uniqueness proof.
and C1, contradicts the consistency of C. This completes the uniqueness proof.
For the converse, suppose that ![[image]](images/eqn957.jpg) . Suppose, by way of contradiction, that
. Suppose, by way of contradiction, that ![[image]](images/eqn958.jpg) . Then, by C2,
. Then, by C2, ![[image]](images/eqn959.jpg) for some x′ ≠ x. By the argument above,
for some x′ ≠ x. By the argument above, ![[image]](images/eqn960.jpg) , a contradiction.
, a contradiction.
The rest of this proof is straightforward. I next show that for all formulas ψ of form ![[image]](images/eqn961.jpg) iff
iff ![[image]](images/eqn962.jpg) for all contexts
for all contexts ![[image]](images/eqn963.jpg) . The proof is by induction on the structure of ψ′. Since ψ′ is a Boolean combination of formulas of the form X = x, for the base case, ψ′ has the form X = x. This was handled above. If ψ′ has the form ¬ψ″, then
. The proof is by induction on the structure of ψ′. Since ψ′ is a Boolean combination of formulas of the form X = x, for the base case, ψ′ has the form X = x. This was handled above. If ψ′ has the form ¬ψ″, then
![[image]](images/eqn964.jpg)
If ψ′ has the form ψ1 ∧ ψ2, then
![[image]](images/eqn969.jpg)
The argument if ψ′ has the form ψ1 ∨ ψ2 is similar to that for ψ1 ∧ ψ2, using axiom C6(c), and is left to the reader.
Finally, we need to consider the case that ψ is a Boolean combination of formulas of the form ![[image]](images/eqn973.jpg) . We again proceed by induction on structure. The argument is similar to that above and is left to the reader.
. We again proceed by induction on structure. The argument is similar to that above and is left to the reader.
There is one more thing that needs to be checked: that ![[image]](images/eqn974.jpg) . Since every instance of C5 is in C, every instance of C5 is true in
. Since every instance of C5 is in C, every instance of C5 is true in ![[image]](images/eqn975.jpg) for all contexts
for all contexts ![[image]](images/eqn976.jpg) . We just need to observe that this guarantees that M is recursive. Define a relation ⪯′ on the endogenous variables by taking
. We just need to observe that this guarantees that M is recursive. Define a relation ⪯′ on the endogenous variables by taking ![[image]](images/eqn977.jpg) . It is easy to see that ⪯′ is reflexive; we must have
. It is easy to see that ⪯′ is reflexive; we must have ![[image]](images/eqn978.jpg) . Let ⪯ be the transitive closure of ⪯′: that is ⪯, is the smallest transitive relation (“smallest” in the sense of relating the fewest pairs of elements) that includes ⪯′. It is well known (and easy to check) that X ⪯ Y iff there exists X0,…, Xn such that X = X0, Y = Xn, X0 ⪯′ X1, X1 ⪯′ X2,…, Xn−1 ⪯′ Xn. (The relation ⪯′ defined this way extends ⪯ and is easily seen to be transitive; moreover, any transitive relation that extends ⪯ must also extend ⪯′.)
. Let ⪯ be the transitive closure of ⪯′: that is ⪯, is the smallest transitive relation (“smallest” in the sense of relating the fewest pairs of elements) that includes ⪯′. It is well known (and easy to check) that X ⪯ Y iff there exists X0,…, Xn such that X = X0, Y = Xn, X0 ⪯′ X1, X1 ⪯′ X2,…, Xn−1 ⪯′ Xn. (The relation ⪯′ defined this way extends ⪯ and is easily seen to be transitive; moreover, any transitive relation that extends ⪯ must also extend ⪯′.)
By construction, ⪯ is reflexive and transitive. Axiom C5 guarantees that it is antisymmetric. For suppose, by way of contradiction, that X ⪯ Y and Y ⪯ X for distinct variables X and Y. Then there exist variables X0,…, Xn and Y0,…, Ym such that X = X0 = Ym, Y = Xn = Y0, X0 ⪯′ X1,…, Xn−1 ⪯′ Xn, Y0 ⪯′ Y1,…, Ym−1 ⪯′ Ym. But then
![[image]](images/eqn978a.jpg)
Finally, the definition of ⤳ guarantees that X affects Y iff ![[image]](images/eqn979.jpg) in some context
in some context ![[image]](images/eqn980.jpg) . Thus,
. Thus, ![[image]](images/eqn981.jpg) , as desired (and, in fact, the same “affects” ordering ⪯ on endogenous variables can be used in all contexts). ■
, as desired (and, in fact, the same “affects” ordering ⪯ on endogenous variables can be used in all contexts). ■
Theorem 5.4.3: A formula ![[image]](images/eqn982.jpg) is satisfiable in
is satisfiable in ![[image]](images/eqn983.jpg) iff there exists
iff there exists ![[image]](images/eqn984.jpg) such that φ is satisfiable in
such that φ is satisfiable in ![[image]](images/eqn985.jpg) .
.
Proof: Clearly, if a formula is satisfiable in ![[image]](images/eqn986.jpg) , then it is satisfiable in
, then it is satisfiable in ![[image]](images/eqn987.jpg) . We can easily convert a causal model
. We can easily convert a causal model ![[image]](images/eqn988.jpg) satisfying φ to a causal model
satisfying φ to a causal model ![[image]](images/eqn989.jpg) satisfying φ by simply defining
satisfying φ by simply defining ![[image]](images/eqn990.jpg) to be a constant, independent of its arguments, for
to be a constant, independent of its arguments, for ![[image]](images/eqn991.jpg) ; if
; if ![[image]](images/eqn992.jpg) , define
, define ![[image]](images/eqn993.jpg) , where
, where ![[image]](images/eqn994.jpg) and
and ![[image]](images/eqn995.jpg) .
.
For the converse, suppose that φ is satisfiable in a causal model ![[image]](images/eqn996.jpg) . Thus,
. Thus, ![[image]](images/eqn997.jpg) for some context
for some context ![[image]](images/eqn998.jpg) , and there is a partial ordering
, and there is a partial ordering ![[image]](images/eqn999.jpg) on the variables in
on the variables in ![[image]](images/eqn999a.jpg) such that unless
such that unless ![[image]](images/eqn1000.jpg) , FX is independent of the value of Y in context
, FX is independent of the value of Y in context ![[image]](images/eqn1001.jpg) .
.
This means that we can view FX as a function of ![[image]](images/eqn1002.jpg) and the variables
and the variables ![[image]](images/eqn1003.jpg) such that
such that ![[image]](images/eqn1003a.jpg) . Let
. Let ![[image]](images/eqn1004.jpg) . For convenience, I allow FX to take as arguments only
. For convenience, I allow FX to take as arguments only ![[image]](images/eqn1005.jpg) and the values of the variables in Pre(X), rather than requiring its arguments to include the values of all the variables in
and the values of the variables in Pre(X), rather than requiring its arguments to include the values of all the variables in ![[image]](images/eqn1006.jpg) . Now define functions
. Now define functions ![[image]](images/eqn1007.jpg) for all
for all ![[image]](images/eqn1008.jpg) by induction on
by induction on ![[image]](images/eqn1009.jpg) ; that is, start by defining
; that is, start by defining ![[image]](images/eqn1010.jpg) for the
for the ![[image]](images/eqn1011.jpg) -minimal elements X, whose value is independent of that of all the other variables, and then work up the
-minimal elements X, whose value is independent of that of all the other variables, and then work up the ![[image]](images/eqn1012.jpg) chains. Suppose
chains. Suppose ![[image]](images/eqn1013.jpg) and
and ![[image]](images/eqn1014.jpg) is a vector of values for the variables in
is a vector of values for the variables in ![[image]](images/eqn1015.jpg) . If X is
. If X is ![[image]](images/eqn1016.jpg) -minimal, then define
-minimal, then define ![[image]](images/eqn1017.jpg) . In general, define
. In general, define ![[image]](images/eqn1018.jpg) , where
, where ![[image]](images/eqn1019.jpg) is a vector of values for the variables in Pre(X) defined as follows. If
is a vector of values for the variables in Pre(X) defined as follows. If ![[image]](images/eqn1020.jpg) , then the value of the Y component in
, then the value of the Y component in ![[image]](images/eqn1021.jpg) is the value of the Y component in
is the value of the Y component in ![[image]](images/eqn1022.jpg) ; if
; if ![[image]](images/eqn1023.jpg) , then the value of the Y component in
, then the value of the Y component in ![[image]](images/eqn1024.jpg) is
is ![[image]](images/eqn1025.jpg) . (By the induction hypothesis,
. (By the induction hypothesis, ![[image]](images/eqn1026.jpg) has already been defined.) Let
has already been defined.) Let ![[image]](images/eqn1027.jpg) . It is easy to check that
. It is easy to check that ![[image]](images/eqn1028.jpg) (the ordering of the variables is just
(the ordering of the variables is just ![[image]](images/eqn1029.jpg) restricted to
restricted to ![[image]](images/eqn1030.jpg) ). Moreover, the construction guarantees that if
). Moreover, the construction guarantees that if ![[image]](images/eqn1031.jpg) , then in context
, then in context ![[image]](images/eqn1032.jpg) , the solutions to the equations
, the solutions to the equations ![[image]](images/eqn1033.jpg) and
and ![[image]](images/eqn1034.jpg) are the same when restricted to the variables in
are the same when restricted to the variables in ![[image]](images/eqn1035.jpg) . It follows that
. It follows that ![[image]](images/eqn1036.jpg) . ■
. ■
Theorem 5.4.4: Given as input a pair (φ, ![[image]](images/eqn1037.jpg) ), where
), where ![[image]](images/eqn1038.jpg) and
and ![[image]](images/eqn1039.jpg) is a finite signature, the problem of deciding if φ is satisfiable in
is a finite signature, the problem of deciding if φ is satisfiable in ![[image]](images/eqn1040.jpg) is NP-complete.
is NP-complete.
Proof: The NP lower bound is easy; there is an obvious way to encode the satisfiability problem for propositional logic into the satisfiability problem for ![[image]](images/eqn1041.jpg) . Given a propositional formula φ with primitive propositions p1,…, pk, let
. Given a propositional formula φ with primitive propositions p1,…, pk, let ![[image]](images/eqn1042.jpg) , where
, where ![[image]](images/eqn1043.jpg) for i = 1,…, k. Replace each occurrence of the primitive proposition pi in φ with the formula Xi = 1. This gives us a formula φ′ in
for i = 1,…, k. Replace each occurrence of the primitive proposition pi in φ with the formula Xi = 1. This gives us a formula φ′ in ![[image]](images/eqn1044.jpg) . It is easy to see that φ′ is satisfiable in a causal model
. It is easy to see that φ′ is satisfiable in a causal model ![[image]](images/eqn1045.jpg) iff φ is a satisfiable propositional formula.
iff φ is a satisfiable propositional formula.
For the NP upper bound, suppose that we are given (φ, ![[image]](images/eqn1046.jpg) ) with
) with ![[image]](images/eqn1047.jpg) . We want to check whether φ is satisfiable in
. We want to check whether φ is satisfiable in ![[image]](images/eqn1048.jpg) . The basic idea is to guess a causal model M and verify that it indeed satisfies φ. There is a problem with this though. To completely describe a model M, we need to describe the functions FX. However, there may be many variables X in
. The basic idea is to guess a causal model M and verify that it indeed satisfies φ. There is a problem with this though. To completely describe a model M, we need to describe the functions FX. However, there may be many variables X in ![[image]](images/eqn1049.jpg) , and they can have many possible inputs. As we have seen, just describing these functions may take time much longer than polynomial in φ. Part of the solution to this problem is provided by Theorem 5.4.3, which tells us that it suffices to check whether φ is satisfiable in
, and they can have many possible inputs. As we have seen, just describing these functions may take time much longer than polynomial in φ. Part of the solution to this problem is provided by Theorem 5.4.3, which tells us that it suffices to check whether φ is satisfiable in ![[image]](images/eqn1050.jpg) . In light of this, for the remainder of this part of the proof, I assume without loss of generality that
. In light of this, for the remainder of this part of the proof, I assume without loss of generality that ![[image]](images/eqn1051.jpg) . Moreover, the proof of Theorem 5.4.1 shows that if a formula is satisfiable at all, it is satisfiable in a model where the equations are independent of the exogenous variables.
. Moreover, the proof of Theorem 5.4.1 shows that if a formula is satisfiable at all, it is satisfiable in a model where the equations are independent of the exogenous variables.
This limits the number of variables that we must consider to at most |φ| (the length of the formula φ, viewed a string of symbols). But even this does not solve the problem completely. Since we are not given any bounds on ![[image]](images/eqn1052.jpg) for variables Y in
for variables Y in ![[image]](images/eqn1053.jpg) , even describing the functions FY for the variables Y that appear in φ on all their possible input vectors could take time much more than polynomial in φ. The solution is to give only a short partial description of a model M and show that this suffices.
, even describing the functions FY for the variables Y that appear in φ on all their possible input vectors could take time much more than polynomial in φ. The solution is to give only a short partial description of a model M and show that this suffices.
Let R be the set of all assignments ![[image]](images/eqn1054.jpg) that appear in φ. Say that two causal models M and M′ in
that appear in φ. Say that two causal models M and M′ in ![[image]](images/eqn1055.jpg) agree on R if, for each assignment
agree on R if, for each assignment ![[image]](images/eqn1056.jpg) , the (unique) solutions to the equations in
, the (unique) solutions to the equations in ![[image]](images/eqn1057.jpg) and
and ![[image]](images/eqn1058.jpg) in context
in context ![[image]](images/eqn1059.jpg) are the same. It is easy to see that if M and M′ agree on R, then either both M and M′ satisfy φ in context
are the same. It is easy to see that if M and M′ agree on R, then either both M and M′ satisfy φ in context ![[image]](images/eqn1060.jpg) or neither do. That is, all we need to know about a causal model is how it deals with the relevant assignments—those in R.
or neither do. That is, all we need to know about a causal model is how it deals with the relevant assignments—those in R.
For each assignment ![[image]](images/eqn1061.jpg) , guess a vector
, guess a vector ![[image]](images/eqn1062.jpg) of values for the endogenous variables; intuitively, this is the unique solution to the equations in
of values for the endogenous variables; intuitively, this is the unique solution to the equations in ![[image]](images/eqn1063.jpg) in context
in context ![[image]](images/eqn1064.jpg) . Given this guess, it is easy to check whether φ is satisfied in a model where these guesses are the solutions to the equations. It remains to show that there exists a causal model in
. Given this guess, it is easy to check whether φ is satisfied in a model where these guesses are the solutions to the equations. It remains to show that there exists a causal model in ![[image]](images/eqn1065.jpg) where the relevant equations have these solutions.
where the relevant equations have these solutions.
To do this, we first guess an ordering ≺ on the variables. We can then verify whether the solution vectors ![[image]](images/eqn1066.jpg) guessed for the relevant equations are compatible with ≺, in the sense that it is not the case that there are two solutions
guessed for the relevant equations are compatible with ≺, in the sense that it is not the case that there are two solutions ![[image]](images/eqn1067.jpg) and
and ![[image]](images/eqn1068.jpg) such that some variable X takes on different values in
such that some variable X takes on different values in ![[image]](images/eqn1069.jpg) and
and ![[image]](images/eqn1070.jpg) , but all variables Y such that Y ≺ X take on the same values in
, but all variables Y such that Y ≺ X take on the same values in ![[image]](images/eqn1071.jpg) and
and ![[image]](images/eqn1072.jpg) . It is easy to see that if the solutions are compatible with ≺, then we can define the functions FX for
. It is easy to see that if the solutions are compatible with ≺, then we can define the functions FX for ![[image]](images/eqn1073.jpg) such that all the equations hold and FX is independent of the values of Y if X ≺ Y for all X,
such that all the equations hold and FX is independent of the values of Y if X ≺ Y for all X, ![[image]](images/eqn1074.jpg) . (Note that we never actually have to write out the functions FX, which may take too long; we just have to know that they exist.) To summarize, as long as we can guess some solutions to the relevant equations such that a causal model that has these solutions satisfies φ, and an ordering ≺ such that these solutions are compatible with ≺, then φ is satisfiable in
. (Note that we never actually have to write out the functions FX, which may take too long; we just have to know that they exist.) To summarize, as long as we can guess some solutions to the relevant equations such that a causal model that has these solutions satisfies φ, and an ordering ≺ such that these solutions are compatible with ≺, then φ is satisfiable in ![[image]](images/eqn1075.jpg) . Conversely, if φ is satisfiable in
. Conversely, if φ is satisfiable in ![[image]](images/eqn1076.jpg) , then there clearly are solutions to the relevant equations that satisfy φ and an ordering ≺ such that these solutions are compatible with ≺. (We just take the solutions and the ordering ≺ from M.) This shows that the satisfiability problem for
, then there clearly are solutions to the relevant equations that satisfy φ and an ordering ≺ such that these solutions are compatible with ≺. (We just take the solutions and the ordering ≺ from M.) This shows that the satisfiability problem for ![[image]](images/eqn1077.jpg) is in NP, as desired. ■
is in NP, as desired. ■
The material in Section 5.1 is largely taken from [Halpern and Hitchcock 2013]. References to the literature on Bayesian networks are given in the notes to Chapter 2. Plausibility measures and conditional plausibility measures were defined by Friedman and Halpern [1995]. The notion of algebraic cpm was introduced in [Halpern 2001], where its application to Bayesian networks is also discussed. Specifically, it is shown there how the “technology” of Bayesian networks applies to representations of uncertainty other probability measures, as long as the representation can be viewed as an algebraic cpm.
Glymour et al. [2010] suggest that trying to understand causality through examples is hopeless because the number of models grows exponentially large as the number of variables increases, which means that the examples considered in the literature represent an “infinitesimal fraction” of the possible examples. (They use much the same combinatorial arguments as those outlined at the beginning of the chapter.) They consider and dismiss a number of approaches to restricting the number of models. Interestingly, although they consider Bayesian networks (and advocate their use), they do not point out that by restricting the number of parents of a node, we get only polynomial growth rather than exponential growth in the number of models. That said, I agree with their point that it does not suffice to just look at examples. See Chapter 8 for more discussion of this point.
Pearl [2000] first discusses causality using causal networks and only then considers definitions of causality using structural equations. As I mentioned in the text, the causal network just gives information regarding the (in)dependencies between variables; the equations in a causal model give more information. However, we can augment a (qualitative) Bayesian network with what are called conditional probability tables. These are just the probabilistic analogue of what was done in Table (5.2) in Example 5.2.1: we give the conditional probability of the value of each variable in the Bayesian network given each possible setting of its parents. (Thus, for variables that have no parents, we give the unconditional probability of each value.) In the deterministic case, these probabilities are always either 0 or 1. In this special case, the conditional probability tables can be viewed as defining structural equations; for each variable X, they determine the equation FX characterizing how the value of X depends on the value of each of the other variables. (Of course, since the value of X is independent of variables that are not its parents, we need to define only how the value of X depends on the values of its parents.) Thus, a qualitative Bayesian network augmented with conditional probability tables (which is called a quantitative Bayesian network in [Halpern 2003]) can be viewed as defining a causal model.
Sipser [2012] gives an excellent introduction to complexity theory, including the fact that Sat is NP-complete (which was originally proved by Cook [1971]). The polynomial hierarchy was defined by Stockmeyer [1977]; the complexity class ![[image]](images/eqn1078.jpg) was defined by Papadimitriou and Yannakakis [1982]; this was generalized to
was defined by Papadimitriou and Yannakakis [1982]; this was generalized to ![[image]](images/eqn1079.jpg) by Aleksandrowicz et al. [2014]. Theorem 5.3.1(a) and Theorem 5.3.2(a) were proved by Eiter and Lukasiewicz [2002], using the fact (which they also proved) that causes in the original HP definition are always singletons; Theorem 5.3.1(b) was proved by Aleksandrowicz et al. [2014]; Theorem 5.3.1(c) and Theorem 5.3.2(b) were proved in [Halpern 2015a]. The fact that many large NP-complete problems can now be solved quite efficiently is discussed in detail by Gomes et al. [2008].
by Aleksandrowicz et al. [2014]. Theorem 5.3.1(a) and Theorem 5.3.2(a) were proved by Eiter and Lukasiewicz [2002], using the fact (which they also proved) that causes in the original HP definition are always singletons; Theorem 5.3.1(b) was proved by Aleksandrowicz et al. [2014]; Theorem 5.3.1(c) and Theorem 5.3.2(b) were proved in [Halpern 2015a]. The fact that many large NP-complete problems can now be solved quite efficiently is discussed in detail by Gomes et al. [2008].
The discussion of axiomatizations is mainly taken from [Halpern 2000]. The axioms considered here were introduced by Galles and Pearl [1998]. The technical results in Section 5.4 were originally proved in [Halpern 2000], although there are some slight modifications here. An example is also given there showing that just restricting C5 to the case of k = 1 does not suffice to characterize ![[image]](images/eqn1080.jpg) . The technique of using maximal consistent sets used in the proof of Theorem 5.4.1 is a standard technique in modal logic. A proof of the properties of maximal consistent sets used in the proof of Theorem 5.4.1, as well as more discussion of this technique, can be found in [Fagin, Halpern, Moses, and Vardi 1995, Chapter 3].
. The technique of using maximal consistent sets used in the proof of Theorem 5.4.1 is a standard technique in modal logic. A proof of the properties of maximal consistent sets used in the proof of Theorem 5.4.1, as well as more discussion of this technique, can be found in [Fagin, Halpern, Moses, and Vardi 1995, Chapter 3].
Briggs [2012] has extended the language ![[image]](images/eqn1081.jpg) to allow disjunctions to appear inside the [] (so that we can write, for example, [X ← 1 ∨ Y ← 1](Z = 1)) and to allow nested counterfactuals (so that we can write [X ← 1]([Y ← 1](Z = 1)). She gives semantics to this language in a way that generalizes that given here and provides a sound and complete axiomatization.
to allow disjunctions to appear inside the [] (so that we can write, for example, [X ← 1 ∨ Y ← 1](Z = 1)) and to allow nested counterfactuals (so that we can write [X ← 1]([Y ← 1](Z = 1)). She gives semantics to this language in a way that generalizes that given here and provides a sound and complete axiomatization.
Responsibility and Blame
Responsibility is a unique concept … You may share it with others, but your portion is not diminished.
Hyman G. Rickover
I enjoyed the position I was in as a tennis player. I was to blame when I lost. I was to blame when I won. And I really like that, because I played soccer a lot too, and I couldn’t stand it when I had to blame it on the goalkeeper.
Roger Federer
Up to now I have mainly viewed causality as an all-or-nothing concept. Although that position is mitigated somewhat by the notion of graded causality discussed in Chapter 3, and by the probabilistic notion of causality discussed in Section 2.5, it is still the case that either A is a cause of B or it is not (in a causal setting ![[image]](images/eqn1081a.jpg) ). Graded causality does allow us to think of some causes as being better than others; with probability, we can take a better cause to be one that has a higher probability of being the cause. But we may want to go further.
). Graded causality does allow us to think of some causes as being better than others; with probability, we can take a better cause to be one that has a higher probability of being the cause. But we may want to go further.
Recall the voting scenario from Example 2.3.2, where there are 11 voters. If Suzy wins the vote 6–5, then all the definitions agree that each voter is a cause of Suzy’s victory. Using the notation from the beginning of Section 2.1, in the causal setting (M, u) where V1 = ⋯ = V6 = 1 and V7 = ⋯ = V11 = 0, so each of the first six voters voted for Suzy, and the rest voted for Billy, each of Vi = 1, i = 1,…, 6 is a cause of W = 1 (Suzy’s victory).
Now consider a context where all 11 voters vote for Suzy. Then according to the original and updated HP definition, it is now the case that Vi = 1 is a cause of W = 1 for i = 1,…, 11. But intuitively, we would like to say that each voter in this case is “less” of a cause than in the case of the 6–5 victory. Graded causality doesn’t help here, since it does not allow us to compare degrees of causality across different causal settings; we cannot use graded causality to say that a voter in the case of a 6–5 win is a “better” cause than a voter in the case of an 11–0 win.
To some extent, this problem is dealt with by the modified HP definition. In the case of the 6–5 victory, each voter is still a cause. In the case of the 11–0 victory, each voter is only part of a cause. As observed in Example 2.3.2, each subset J of six voters is a cause; that is, ∧i∈JVi = 1 is a cause of W = 1. Intuitively, being part of a “large” cause should make a voter feel less responsible than being part of a “small” cause. In the next section, I formalize this intuition (for all the variants of the HP definition). This leads to a naive definition of responsibility, which nevertheless captures intuitions reasonably well.
Like the definition of causality, this definition of responsibility assumes that everything relevant about the facts of the world and how the world works is known. Formally, this means that the definition is relative to a causal setting ![[image]](images/eqn1081b.jpg) . But this misses out on an important component of determining what I will call here blame: the epistemic state. Consider a doctor who treats a patient with a particular drug, resulting in the patient’s death. The doctor’s treatment is a cause of the patient’s death; indeed, the doctor may well bear degree of responsibility 1 for the death. However, if the doctor had no idea that the treatment had adverse side effects for people with high blood pressure, then he should perhaps not be blamed for the death. Actually, in legal arguments, it may not be so relevant what the doctor actually did or did not know, but what he should have known. Thus, rather than considering the doctor’s actual epistemic state, it may be more important to consider what his epistemic state should have been. But, in any case, if we are trying to determine whether the doctor is to blame for the patient’s death, we must take into account the doctor’s epistemic state.
. But this misses out on an important component of determining what I will call here blame: the epistemic state. Consider a doctor who treats a patient with a particular drug, resulting in the patient’s death. The doctor’s treatment is a cause of the patient’s death; indeed, the doctor may well bear degree of responsibility 1 for the death. However, if the doctor had no idea that the treatment had adverse side effects for people with high blood pressure, then he should perhaps not be blamed for the death. Actually, in legal arguments, it may not be so relevant what the doctor actually did or did not know, but what he should have known. Thus, rather than considering the doctor’s actual epistemic state, it may be more important to consider what his epistemic state should have been. But, in any case, if we are trying to determine whether the doctor is to blame for the patient’s death, we must take into account the doctor’s epistemic state.
Building on the definition of responsibility, in Section 6.2, I present a definition of blame that considers whether agent a performing action b is to blame for an outcome φ. The definition is relative to an epistemic state for a, which is a set of causal settings, together with a probability on them. The degree of blame is then essentially the expected degree of responsibility of action b for φ. To understand the difference between responsibility and blame, suppose that there is a firing squad consisting of ten excellent marksmen. Only one of them has live bullets in his rifle; the rest have blanks. The marksmen do not know which of them has the live bullets. The marksmen shoot at the prisoner and he dies. The only marksman who is the cause of the prisoner’s death is the one with the live bullets. That marksman has degree of responsibility 1 for the death; all the rest have degree of responsibility 0. However, each of the marksmen has degree of blame 1/10.
The definition of responsibility that I give in Section 6.1 is quite naive, although it does surprisingly well at predicting how people ascribe causal responsibility. However, people depart from this definition in some systematic ways. For one thing, people seem to take normality into account. Thus, to some extent, graded causality is getting at similar intuitions as the notion of responsibility. To make matters worse, people seem to confound blame and responsibility when ascribing responsibility; in particular, they take into account the prior probabilities of the outcome, before the action was performed. All this suggests that there may not be a clean, elegant definition of responsibility that completely matches how people ascribe responsibility. I discuss this in more detail in Section 6.3.
Before going on, a few words on the choice of words. Although I believe that the definitions of “responsibility” and “blame” presented here are reasonable, they certainly do not capture all the connotations of these words as used in the literature or in natural language. In the philosophy literature, papers on responsibility typically are concerned with moral responsibility. The definitions given here, by design, do not take into account intentions or what the alternatives were, both of which seem necessary in dealing with moral issues. (The model implicitly encodes the existence of alternative actions in the range of variables representing actions, but the definition of causality does not take this into account beyond requiring the existence of at least a second alternative before saying that a particular action is a cause of an outcome.)
For example, there is no question that Truman was in part responsible and to blame for the deaths resulting from dropping the atom bombs on Hiroshima and Nagasaki. However, to decide whether this is a morally reprehensible act, it is also necessary to consider the alternative actions he could have performed and their possible outcomes. The definitions given do not address these moral issues, but I believe that they may be helpful in elucidating them.
Although “responsibility” and “blame” as I will define them are distinct notions, these words are often used interchangeably in natural language. Phrases and terms like “degree of causality”, “degree of culpability”, and “accountability” are also used to describe similar notions. I think it is important to tease out the distinctions between notions. However, the reader should be careful not to read too much into my usage of words like “responsibility” and “blame”.
6.1 A Naive Definition of Responsibility
I start by giving a naive definition of responsibility for the original HP definition. I give the definition in causal models without a normality ordering. I briefly remark after the definition how responsibility can be defined in extended causal models.
Definition 6.1.1 The degree of responsibility of X = x for φ in ![[image]](images/eqn1081c.jpg) according to the original HP definition, denoted
according to the original HP definition, denoted ![[image]](images/eqn1082.jpg) , is 0 if X = x is not a cause of φ in
, is 0 if X = x is not a cause of φ in ![[image]](images/eqn1082a.jpg) according to the original HP definition; it is 1/(k + 1) if there is a witness (
according to the original HP definition; it is 1/(k + 1) if there is a witness (![[image]](images/eqn1083.jpg) ,
, ![[image]](images/eqn1084.jpg) , x′) to X = x being a cause of φ in
, x′) to X = x being a cause of φ in ![[image]](images/eqn1085.jpg) according to the original HP definition, and k is minimal, in that there is no witness (
according to the original HP definition, and k is minimal, in that there is no witness (![[image]](images/eqn1086.jpg) ,
, ![[image]](images/eqn1087.jpg) , x′) to X = x being a cause of φ in (M,
, x′) to X = x being a cause of φ in (M, ![[image]](images/eqn1088.jpg) ) according to the original HP definition such that
) according to the original HP definition such that ![[image]](images/eqn1089.jpg) . ■
. ■
Of course, if we consider extended causal models, we should restrict to witnesses (![[image]](images/eqn1090.jpg) ,
, ![[image]](images/eqn1091.jpg) , x′) such that
, x′) such that ![[image]](images/eqn1092.jpg) . (Recall this condition says that the witness world is at least as normal as the actual world.) Doing this does not change any of the essential features of the definition, so I do not consider the normality ordering further in this section. I consider its impact more carefully in Section 6.3.
. (Recall this condition says that the witness world is at least as normal as the actual world.) Doing this does not change any of the essential features of the definition, so I do not consider the normality ordering further in this section. I consider its impact more carefully in Section 6.3.
Roughly speaking, ![[image]](images/eqn1093.jpg) measures the minimal number of changes that have to be made to the world
measures the minimal number of changes that have to be made to the world ![[image]](images/eqn1094.jpg) in order to make φ counterfactually depend on X. If X = x is not a cause of φ, then no partition of
in order to make φ counterfactually depend on X. If X = x is not a cause of φ, then no partition of ![[image]](images/eqn1095.jpg) to
to ![[image]](images/eqn1096.jpg) makes φ counterfactually depend on X = x, and the minimal number of changes in Definition 6.1.1 is taken to have cardinality ∞; thus, the degree of responsibility of X = x is 0. If φ counterfactually depends on X = x, that is, X = x is a but-for cause of φ in (M,
makes φ counterfactually depend on X = x, and the minimal number of changes in Definition 6.1.1 is taken to have cardinality ∞; thus, the degree of responsibility of X = x is 0. If φ counterfactually depends on X = x, that is, X = x is a but-for cause of φ in (M, ![[image]](images/eqn1098.jpg) ), then the degree of responsibility of X = x in φ is 1. In other cases, the degree of responsibility is strictly between 0 and 1. Thus, X = x is a cause of φ in (M,
), then the degree of responsibility of X = x in φ is 1. In other cases, the degree of responsibility is strictly between 0 and 1. Thus, X = x is a cause of φ in (M, ![[image]](images/eqn1099.jpg) ) according to the original HP definition iff
) according to the original HP definition iff ![[image]](images/eqn1100.jpg) .
.
Example 6.1.2 Going back to the voting example, it is immediate that each voter who votes for Suzy has degree of responsibility 1 in the case of a 6–5 victory. Each voter for Suzy is a but-for cause of the outcome; changing any of their votes is enough to change the outcome. However, in the case of an 11–0 victory, each voter has degree of responsibility 1/6. To see that the degree of responsibility of, say, V1 = 1 for W = 1 is 1/6 in the latter case, we could, for example, take ![[image]](images/eqn1101.jpg) and
and ![[image]](images/eqn1102.jpg) . Clearly,
. Clearly, ![[image]](images/eqn1103.jpg) is a witness to V1 = 1 being a cause of W = 1. There are many other witnesses, but none has a set
is a witness to V1 = 1 being a cause of W = 1. There are many other witnesses, but none has a set ![[image]](images/eqn1106.jpg) of smaller cardinality.
of smaller cardinality.
As this example illustrates, the sum of the degrees of responsibility can be more than 1. The degree of responsibility is not a probability!
Example 6.1.3 Consider the forest-fire example yet again. In the conjunctive model, both the lightning and the arsonist have degree of responsibility 1 for the fire; changing either one results in there being no fire. In the disjunctive model, they both have degree of responsibility 1/2. Thus, degree of responsibility lets us distinguish the two scenarios even though, according to the original HP definitions, the lightning and the arsonist are causes of the fire in both scenarios. ■
The intuition that ![[image]](images/eqn1107.jpg) is the minimal number of changes that has to be made in order to make φ counterfactually depend on X is not completely right, as the following example shows.
is the minimal number of changes that has to be made in order to make φ counterfactually depend on X is not completely right, as the following example shows.
Example 6.1.4 Consider a model with three endogenous variables, A, B, and C. The value of A is determined by the context, B takes the same value as A, and C is 0 if A and B agree, and 1 otherwise. The context u is such that A = 0, so B = 0 and C = 0. A = 0 is a cause of C = 0 according to the original HP definition, with witness ({B}, 0, 1): if we fix B at 0, then if A = 1, C = 1. It is easy to check that (∅, ∅, 1) is not a witness. Thus, the degree of responsibility of A = 0 is 1/2. However, the value of B did not have to change in order to make C depend counterfactually on A; rather, B had to be held at its actual value. ■
Example 6.1.5 In the naive model of the rock-throwing example, Suzy and Billy each have degree of responsibility 1/2 for the bottle shattering. In the sophisticated model, Suzy has degree of responsibility 1/2 for the outcome, since the the minimal witness for ST = 1 being a cause of BS = 1 consists of BH (or BT). In contrast, Billy has degree of responsibility 0 for the bottle shattering, since his throw was not a cause of the outcome. ■
These examples also suggest how to define degree of responsibility of X = x for φ in (M, ![[image]](images/eqn1108.jpg) ) for the modified and updated HP definitions. Now a cause can involve a set of variables, not just a single variable. Both the size of the cause and the size of the witness matter for computing the degree of responsibility.
) for the modified and updated HP definitions. Now a cause can involve a set of variables, not just a single variable. Both the size of the cause and the size of the witness matter for computing the degree of responsibility.
Definition 6.1.6 The degree of responsibility of X = x for φ in (M, ![[image]](images/eqn1109.jpg) ) according to the updated (resp., modified) HP definition, denoted
) according to the updated (resp., modified) HP definition, denoted ![[image]](images/eqn1110.jpg) (resp.,
(resp., ![[image]](images/eqn1111.jpg) , is 0 if X = x is not part of a cause of φ in (M,
, is 0 if X = x is not part of a cause of φ in (M, ![[image]](images/eqn1112.jpg) ) according to the updated (resp., modified) HP definition; it is 1/k if there exists a cause
) according to the updated (resp., modified) HP definition; it is 1/k if there exists a cause ![[image]](images/eqn1113.jpg) of φ and a witness (
of φ and a witness (![[image]](images/eqn1114.jpg) ,
, ![[image]](images/eqn1115.jpg) ,
, ![[image]](images/eqn1116.jpg) ) to
) to ![[image]](images/eqn1117.jpg) being a cause of φ in (M,
being a cause of φ in (M, ![[image]](images/eqn1118.jpg) ) such that (a) X = x is a conjunct of
) such that (a) X = x is a conjunct of ![[image]](images/eqn1119.jpg) , (b)
, (b) ![[image]](images/eqn1120.jpg) , and (c) k is minimal, in that there is no cause
, and (c) k is minimal, in that there is no cause ![[image]](images/eqn1121.jpg) for φ in (M,
for φ in (M, ![[image]](images/eqn1122.jpg) ) and witness (
) and witness (![[image]](images/eqn1123.jpg) ,
, ![[image]](images/eqn1124.jpg) ,
, ![[image]](images/eqn1125.jpg) ) to
) to ![[image]](images/eqn1126.jpg) being a cause of φ in (M,
being a cause of φ in (M, ![[image]](images/eqn1128.jpg) ) according to the updated (resp., modified) HP definition that includes X = x as a conjunct with
) according to the updated (resp., modified) HP definition that includes X = x as a conjunct with ![[image]](images/eqn1129.jpg) . ■
. ■
It is easy to see that all the definitions of degree of responsibility agree that the degree of responsibility is 1/6 for each voter in the case of the 11–0 vote; that A = 0 has degree of responsibility 1/2 for C = 0 in the causal settings described in Example 6.1.4; that Suzy has degree of responsibility 1/2 for the bottle shattering in both the naive and sophisticated rock-throwing examples; that the lightning and arsonist both have degree of responsibility 1/2 in the disjunctive forest-fire model; and that they both have degree of responsibility 1 in the conjunctive forest-fire model. If the distinction between the various HP definitions of causality is not relevant for the degree of responsibility, I just write dr, omitting the superscript.
These examples already suggest that this definition of responsibility does capture some of the way people use the word. But this definition is admittedly somewhat naive. I look at it more carefully, and consider refinements of it, in Section 6.3. But first I consider blame.
The definitions of both causality and responsibility assume that the context and the structural equations are given; there is no uncertainty. We are often interested in assigning a degree of blame to an action. This assignment depends on the epistemic state of the agent before the action was performed. Intuitively, if the agent had no reason to believe, before he performed the action, that his action would result in a particular outcome, then he should not be held to blame for the outcome (even if in fact his action caused the outcome).
There are two significant sources of uncertainty for an agent who is contemplating performing an action:
In a causal model, the values of variables is determined by the context; “how the world works” is determined by the structural equations. Thus, I model an agent’s uncertainty by a pair (![[image]](images/eqn1130.jpg) , Pr), where
, Pr), where ![[image]](images/eqn1131.jpg) is a set of causal settings, that is, pairs of the form (M,
is a set of causal settings, that is, pairs of the form (M, ![[image]](images/eqn1132.jpg) ), and Pr is a probability distribution over
), and Pr is a probability distribution over ![[image]](images/eqn1133.jpg) . If we are trying to assign a degree of blame to X = x, then we assume that X = x holds in all causal settings in
. If we are trying to assign a degree of blame to X = x, then we assume that X = x holds in all causal settings in ![[image]](images/eqn1134.jpg) ; that is,
; that is, ![[image]](images/eqn1135.jpg) for all
for all ![[image]](images/eqn1136.jpg) ). The assumption is that X = x is known;
). The assumption is that X = x is known; ![[image]](images/eqn1137.jpg) describes the uncertainty regarding other features of the world. We typically think of
describes the uncertainty regarding other features of the world. We typically think of ![[image]](images/eqn1138.jpg) as describing an agent’s uncertainty before he has actually performed X = x, so I do not take φ to be known (although in many cases of interest, it will be);
as describing an agent’s uncertainty before he has actually performed X = x, so I do not take φ to be known (although in many cases of interest, it will be); ![[image]](images/eqn1139.jpg) could also be taken to describe the agent’s uncertainty after performing X = x and making observations regarding the effect of this action (which will typically include φ). I return to this point below (see Example 6.2.4). In any case, the degree of blame of X = x for φ is just the expected degree of responsibility of X = x for φ, where the expectation is taken with respect to Pr. Just as there is a definition of degree of responsibility corresponding to each variant of the HP definition, there are definitions of degree of blame corresponding to each variant. Here I ignore these distinctions and just write dr for degree of responsibility (omitting the superscript) and db for the notion of degree of blame (again, omitting the corresponding superscript).
could also be taken to describe the agent’s uncertainty after performing X = x and making observations regarding the effect of this action (which will typically include φ). I return to this point below (see Example 6.2.4). In any case, the degree of blame of X = x for φ is just the expected degree of responsibility of X = x for φ, where the expectation is taken with respect to Pr. Just as there is a definition of degree of responsibility corresponding to each variant of the HP definition, there are definitions of degree of blame corresponding to each variant. Here I ignore these distinctions and just write dr for degree of responsibility (omitting the superscript) and db for the notion of degree of blame (again, omitting the corresponding superscript).
Definition 6.2.1 The degree of blame of X = x for φ relative to epistemic state (![[image]](images/eqn1140.jpg) , Pr), denoted db(
, Pr), denoted db(![[image]](images/eqn1141.jpg) , Pr, X = x, φ), is
, Pr, X = x, φ), is
![[image]](images/eqn1142.jpg)
Example 6.2.2 Suppose that we are trying to compute the degree of blame of Suzy’s throwing the rock for the bottle shattering. Suppose that the only causal model that Suzy considers possible is essentially like that of Figure 2.3, with some minor modifications: BT can now take on three values, say 0, 1, 2. As before, if BT = 0, then Billy doesn’t throw, and if BT = 1, then Billy does throw; if BT = 2, then Billy throws extra hard. Assume that the causal model is such that if BT = 1, then Suzy’s rock will hit the bottle first, but if BT = 2, then they will hit simultaneously. Thus, SH = 1 if ST = 1, and BH = 1 if BT = 1 and SH = 0 or if BT = 2. Call this structural model M.
At time 0, Suzy considers the following four causal settings equally likely:
![[image]](images/eqn1143.jpg) ), where
), where ![[image]](images/eqn1144.jpg) is such that Billy already threw at time 0 (and hence the bottle is shattered);
is such that Billy already threw at time 0 (and hence the bottle is shattered);![[image]](images/eqn1145.jpg) ), where the bottle was whole before Suzy’s throw, and Billy throws extra hard, so Billy’s throw and Suzy’s throw hit the bottle simultaneously (this essentially gives the model in Figure 2.2);
), where the bottle was whole before Suzy’s throw, and Billy throws extra hard, so Billy’s throw and Suzy’s throw hit the bottle simultaneously (this essentially gives the model in Figure 2.2);![[image]](images/eqn1146.jpg) ), where the bottle was whole before Suzy’s throw, and Suzy’s throw hit before Billy’s throw (this essentially gives the model in Figure 2.3); and
), where the bottle was whole before Suzy’s throw, and Suzy’s throw hit before Billy’s throw (this essentially gives the model in Figure 2.3); and![[image]](images/eqn1147.jpg) ), where the bottle was whole before Suzy’s throw, and Billy did not throw.
), where the bottle was whole before Suzy’s throw, and Billy did not throw.The bottle is already shattered in (M, ![[image]](images/eqn1148.jpg) ) before Suzy’s action, so Suzy’s throw is not a cause of the bottle shattering, and her degree of responsibility for the shattered bottle is 0. As discussed earlier, the degree of responsibility of Suzy’s throw for the bottle shattering is 1/2 in both (M,
) before Suzy’s action, so Suzy’s throw is not a cause of the bottle shattering, and her degree of responsibility for the shattered bottle is 0. As discussed earlier, the degree of responsibility of Suzy’s throw for the bottle shattering is 1/2 in both (M, ![[image]](images/eqn1149.jpg) ) and (M,
) and (M, ![[image]](images/eqn1150.jpg) ) and 1 in (M,
) and 1 in (M, ![[image]](images/eqn1151.jpg) ). Thus, the degree of blame of ST = 1 for
). Thus, the degree of blame of ST = 1 for ![[image]](images/eqn1152.jpg) . ■
. ■
Example 6.2.3 Consider again the example of the firing squad with ten excellent marksmen. Suppose that marksman 1 knows that exactly one marksman has a live bullet in his rifle and that all the marksmen will shoot. Thus, he considers 10 contexts possible, depending on who has the bullet. Let pi be his prior probability that marksman i has the live bullet. Then the degree of blame (according to marksman 1) of the ith marksman’s shot for the death is pi. The degree of responsibility is either 1 or 0, depending on whether marksman i actually had the live bullet. Thus, it is possible for the degree of responsibility to be 1 and the degree of blame to be 0 (if marksman 1 mistakenly ascribes probability 0 to his having the live bullet, when in fact he does), and it is possible for the degree of responsibility to be 0 and the degree of blame to be 1 (if he mistakenly ascribes probability 1 to his having the bullet when in fact he does not). ■
As I said earlier, typically the probability Pr on the set ![[image]](images/eqn1153.jpg) of causal settings can be thought of as being the agent’s prior probability, before observing the consequences of having X = x. But it makes perfect sense to take other choices for Pr. For example, it could be the agent’s posterior probability, after making observations. In legal settings, it might be important to consider not the agent’s actual prior (or posterior) probability—that is, the agent’s actual epistemic state—but what the agent’s probability should have been. The definition of degree of blame does not change, however Pr is interpreted; it just takes the probability Pr as an input. But the choice can clearly affect the degree of blame computed. The following example illustrates some of the key differences.
of causal settings can be thought of as being the agent’s prior probability, before observing the consequences of having X = x. But it makes perfect sense to take other choices for Pr. For example, it could be the agent’s posterior probability, after making observations. In legal settings, it might be important to consider not the agent’s actual prior (or posterior) probability—that is, the agent’s actual epistemic state—but what the agent’s probability should have been. The definition of degree of blame does not change, however Pr is interpreted; it just takes the probability Pr as an input. But the choice can clearly affect the degree of blame computed. The following example illustrates some of the key differences.
Example 6.2.4 Consider a patient who dies as a result of being treated by a doctor with a particular drug. Assume that the patient died due to the drug’s adverse side effects on people with high blood pressure and, for simplicity, that this was the only cause of death. Suppose that the doctor was not aware of the drug’s adverse side effects. (Formally, this means that he does not consider possible a causal model where taking the drug causes death.) Then, relative to the doctor’s actual epistemic state, the doctor’s degree of blame will be 0. The key point here is that the doctor will ascribe high probability to causal setting in ![[image]](images/eqn1154.jpg) where he treats the patient and the patient does not die. However, a lawyer might argue in court that the doctor should have known that this treatment had adverse side effects for patients with high blood pressure (because this fact is well documented in the literature) and thus should have checked the patient’s blood pressure. If the doctor had performed this test, then he would of course have known that the patient had high blood pressure. With respect to the resulting epistemic state, the doctor’s degree of blame for the death is quite high. Of course, the lawyer’s job is to convince the court that the latter epistemic state is the appropriate one to consider when assigning degree of blame.
where he treats the patient and the patient does not die. However, a lawyer might argue in court that the doctor should have known that this treatment had adverse side effects for patients with high blood pressure (because this fact is well documented in the literature) and thus should have checked the patient’s blood pressure. If the doctor had performed this test, then he would of course have known that the patient had high blood pressure. With respect to the resulting epistemic state, the doctor’s degree of blame for the death is quite high. Of course, the lawyer’s job is to convince the court that the latter epistemic state is the appropriate one to consider when assigning degree of blame.
In any case, the doctor’s actual epistemic state and the epistemic state he arguably should have had before observing the effects of the drug might both be different from his epistemic state after treating the patient with the drug and observing that he dies. Not knowing the literature, the doctor may still consider it possible that the patient died for reasons other than the treatment, but will consider causal models where the treatment was a cause of death more likely. Thus, the doctor will likely have a higher degree of blame relative to his epistemic state after the treatment. ■
Interestingly, all three epistemic states (the epistemic state that an agent actually has before performing an action, the epistemic state that the agent should have had before performing the action, and the epistemic state after performing the action) have been considered relevant to determining responsibility according to different legal theories. Thinking in terms of the relevant epistemic state also helps clarify some earlier examples that seemed problematic.
Example 6.2.5 Recall Example 2.3.8, where company A dumps 100 kilograms of pollutant, company B dumps 60 kilograms, and biologists determine that k kilograms of pollutant suffice for the fish to die. The “problematic” case was when k = 80. In this case, only A is a cause of the fish dying according to the modified HP definition. A is also a cause according to the original and updated HP definition; whether B is a cause depends on whether A’s only choices are to dump either 0 or 100 kilograms of pollutant (in which case B is not a cause) or whether A can dump some intermediate amount between 20 and 79 kilograms (in which case B is a cause).
Although it may not be clear what the “right” answer is here, it does seem disconcerting that B escapes responsibility if we use the modified HP definition, and that B’s degree of responsibility should depend so heavily on the amount of pollutant that A could have dumped in the case of the original and updated definition. Thinking in terms of blame gives what seem to be more reasonable answers here. When trying to decide how blameworthy B’s action is, we typically do not think that B will know exactly how much pollutant A will dump, nor that B will know how much pollutant is needed to kill fish. A causal model for B can thus be characterized by two parameters: the amount a of pollutant that A dumps and the amount k of pollutant that is needed to kill the fish. We can now consider B’s degree of responsibility in a causal model as a function of a and k:
The point here is that with reasonable assumptions about what B’s state of mind should have been, no matter which variant of the HP definition we use, B gets a positive degree of blame. The degree of blame is likely to depend on factors like how close k is to 60 and the difference between a and k; that is, how close B was to making a difference. This indeed seems to track how juries might assign blame. Moreover, if company B could convince the jury that, before dumping pollutant, it had hard evidence that company A had already dumped more than k kilograms of pollutant (so that B was certain that its act would make no difference), then there is a good chance that the jury would ascribe less blame to B. (Of course, a jury may still want to punish B for the deterrent value of the punishment, but that is a matter orthogonal to the notion of blame that is being captured here.)
Similar considerations show that, under minimal assumptions, if the amount of pollutant dumped by A and B is known, but there is uncertainty about k, then A’s degree of blame will be higher than that of B. This again seems to accord with intuition. ■
Example 6.2.6 Voting has often been viewed as irrational. After all, the probability that one individual’s vote can affect the outcome is typically extremely small. Indeed, the probability that an individual’s vote can affect the outcome of the U.S. presidential election has been calculated to be roughly 10−8. (Of course, if almost everyone decides not to vote on the grounds that their vote is extremely unlikely to affect the outcome, then the few people who actually vote will have a major impact on the outcome.)
In any case, people clearly do vote. There has been a great deal of work trying to explain why people vote and defining reasonable utilities that people might have that would make voting rational. One approach that I find compelling is that people feel a certain degree of responsibility for the outcome. Indeed, in a 2-candidate race where A gets a votes and B gets b votes, with a > b, assuming that it requires a majority to win, all the approaches agree that a voter for A has degree of responsibility ![[image]](images/eqn1155.jpg) for the outcome (where ⌈x⌉ is the smallest integer greater than or equal to x, so that, for example, ⌈5/2⌉ = 3 and ⌈3⌉ = 3). Thus, in an 11-0 victory, each voter has degree of responsibility 1/6, since ⌈1/2⌉ = 6, and in a 6–5 victory, each voter has degree of responsibility 1. Each voter can then carry out an analysis in the spirit of Example 6.2.5 to compute his degree of blame for the outcome. The argument goes that he should then vote because he bears some degree of responsibility/blame for the outcome.
for the outcome (where ⌈x⌉ is the smallest integer greater than or equal to x, so that, for example, ⌈5/2⌉ = 3 and ⌈3⌉ = 3). Thus, in an 11-0 victory, each voter has degree of responsibility 1/6, since ⌈1/2⌉ = 6, and in a 6–5 victory, each voter has degree of responsibility 1. Each voter can then carry out an analysis in the spirit of Example 6.2.5 to compute his degree of blame for the outcome. The argument goes that he should then vote because he bears some degree of responsibility/blame for the outcome.
Of course, it then seems reasonable to ask how that degree of responsibility and blame change depending on whether he votes. There is an intuition that someone who abstains should be less responsible for an outcome than someone who votes for it. Although certainly someone who abstains can never be more responsible for an outcome than someone who votes for it, they may be equally responsible. For example, if we take ties to be undecided and Suzy wins a 6–5 vote against Billy where there is one abstention, then the abstainer and each of the six voters for Suzy are but-for causes of the outcome and thus have degree of responsibility 1. If the vote is 7–5 for Suzy with one abstention, then again each of the voters for Suzy has degree of responsibility 1 for all variants of the HP definition, since they are but-for cause of the outcome. However, the abstainer has degree of responsibility 1/2: if a voter for Suzy abstains, then the abstainer’s vote becomes critical, since he can make the outcome a draw by voting for Billy.
More generally, if a voters vote for Suzy, b voters vote for Billy, c voters abstain, and a > b, then, as we have seen, the degree of responsibility of one of Suzy’s voters for the outcome is ![[image]](images/eqn1156.jpg) . If a − b is odd, this is also the degree of responsibility of an abstainer. However, if a − b is even and c ≥ 2, then the degree of responsibility of an abstainer is slightly lower:
. If a − b is odd, this is also the degree of responsibility of an abstainer. However, if a − b is even and c ≥ 2, then the degree of responsibility of an abstainer is slightly lower: ![[image]](images/eqn1157.jpg) . Finally, if a − b is even and c = 1, then the abstainer has degree of responsibility 0 for all variants of the HP definition. To understand why this should be so, suppose that the vote is 9–5 with 2 abstentions. Then if we switch one of the voters for Suzy to voting for Billy and switch one abstainer to voting for Billy, then the vote becomes 8–7; now if the second abstainer votes for Billy, Suzy is no longer the winner. Thus, the second abstainer has degree of responsibility 1/3 for Suzy’s victory. However, if there is only one abstention, there are no vote flips that would make the abstainer critical; the abstainer is not a cause of the outcome. This argument applies to all the variants of the HP definition.
. Finally, if a − b is even and c = 1, then the abstainer has degree of responsibility 0 for all variants of the HP definition. To understand why this should be so, suppose that the vote is 9–5 with 2 abstentions. Then if we switch one of the voters for Suzy to voting for Billy and switch one abstainer to voting for Billy, then the vote becomes 8–7; now if the second abstainer votes for Billy, Suzy is no longer the winner. Thus, the second abstainer has degree of responsibility 1/3 for Suzy’s victory. However, if there is only one abstention, there are no vote flips that would make the abstainer critical; the abstainer is not a cause of the outcome. This argument applies to all the variants of the HP definition.
We can “smooth away” this dependence on the parity of a – b and on whether c = 1 or c > 1 by considering the degree of blame. Under minimal assumptions, the degree of blame of an abstainer will be (slightly) less than that of a voter for the victor.
Is the increase in degree of blame for the outcome (here perhaps “responsibility” is a better word) enough to get someone to vote? Perhaps people don’t consider the increase in degree of blame/responsibility when deciding whether to vote; rather, they say (correctly) that they feel responsible for the outcome if they vote and believe that that’s a good thing. The impact of responsibility on voting behavior deserves further investigation. ■
![[image]](images/fig6-1.jpg)
Figure 6.1: Attenuation in a causal chain.
Example 6.2.7 Recall the causal chain example from Section 3.4.4. The causal network for this example is reproduced in Figure 6.1. Although both M = 1 and LL = 1 are causes of ES = 1 according to all the variants of the HP definition (indeed, they are but-for causes), taking graded causality into account, the original and updated HP definition captured the attenuation of causality along the chain. A cause close to the outcome, like LL = 1, is viewed as being a better cause than one further away, like M = 1. The modified HP definition was not able to obtain this result.
However, once we take blame into account and make reasonable assumptions about an agent’s probability distribution on causal models, all the definitions again agree that LL = 1 is more to blame for the outcome than M = 1. Recall that in the actual context in this example, M = R = F = LI = EU = 1, so all the variables are 1. However, the equations are such that if any of these variables is 0, then ES = 0. Now suppose that an agent is uncertain as to the values of these variables. That is, although the agent knows the causal model, he is uncertain about the context. For all variants of the HP definition, LL = 1 is a cause (and hence has degree of responsibility 1) in all causal settings where EU = 1, and otherwise is not a cause. Similarly, M = 1 is a cause and has degree of responsibility 1 in the causal setting where R = F = LI = EU = 1, and otherwise is not a cause. Again, under minimal assumptions, the degree of blame of M = 1 for ES = 1 is strictly less than that of LL = 1 (and, more generally, attenuates as we go along the chain). ■
Example 6.2.8 Consider the classic bystander effect: A victim is attacked and is in need of help. The probability that someone helps is inversely related to the number of bystanders: the greater the number of bystanders, the less likely one of them is to help. The bystander effect has often been explained in terms of “diffusion of responsibility” and the degree of responsibility that a bystander feels.
Suppose for simplicity that as long as one bystander gets involved, the victim will be saved; otherwise the victim will die. That means that if no one gets involved, each bystander is a cause of the victim’s death and has degree of responsibility 1. This seems inconsistent with the intuition that the more bystanders there are, the less responsibility a bystander feels. It actually seems that the notion of blame as I have defined it is capturing the intuition here, rather than the notion of responsibility. (Recall my earlier comment that English tends to use these words interchangeably.)
For suppose that we assume that a bystander sees n other bystanders and is deciding whether to get involved. Further suppose (as seems quite plausible) that there is a significant cost to being involved in terms of time, so, all things being equal, the bystander would prefer not to be involved. However, the bystander does not want to get blamed for the outcome. Of course, if he gets involved, then he will not be blamed. If he does not get involved, then his degree of blame will depend on what others do. The lower his perceived blame, the less likely the bystander is to get involved. Thus, the bystander must compute his degree of blame if he does not get involved. Assume that which other bystanders will get involved is determined by the context. Note that a bystander who gets involved has degree of responsibility 1/(k + 1) for the victim surviving in a causal setting where k other bystanders get involved; a bystander who does not get involved has degree of responsibility 0 for the victim surviving. Getting an accurate model of how many other bystanders will get involved is, of course, rather complicated (especially since other bystanders might be thinking along similar lines). But for our purposes, it suffices that bystanders assume that the more bystanders there are, for each k > 0, the more likely it is that at least k bystanders will get involved. With this assumption, the bystander’s degree of blame decreases the more bystanders there are. If he uses the rule of getting involved only if his degree of blame (i.e., expected degree of responsibility) for the victim’s survival is greater than some threshold, and uses this naive analysis to compute degree of blame (which does not seem so unreasonable in the heat of the moment), then the more bystanders there are, the less likely he is to get involved. ■
6.3 Responsibility, Normality, and Blame
The definition of responsibility given in Section 6.1 is rather naive. Nevertheless, experiments have shown that it does give qualitatively reasonable results in many cases. For example, when asked to judge the degree of responsibility of a voter for a victory, they give each voter lower and lower responsibility as the outcome goes from 1–0 to 4–0 (although it is certainly not the case that they ascribe degree of responsibility 1 in the case of a 2–0 and 1/2 in the case of a 3–0 victory, as the naive definition would suggest). However, this definition does not capture all aspects of how people attribute responsibility. In this section, I discuss some systematic ways in which people’s responsibility attributions deviate from this definition and suggest some improvements to the definition that takes them into account.
One problem with the naive definition of responsibility is that it is clearly language dependent, as the following example shows.
Example 6.3.1 Consider a vote where there are two large blocs: bloc A controls 25 votes and bloc B controls 25 votes. As the name suggests, all the voters in a bloc vote together, although in principle, they could vote differently. There is also one independent voter; call her C. A measure passes unanimously, by a vote of 51–0. What is the degree of responsibility of C for the outcome? If the only variables in the model are A, B, C, and O (for outcome), then it is 1/2; we need to change either A or B’s vote to make C’s vote critical. But this misses out on the fact that A and B each made a more significant contribution to the outcome than C. If instead we use variables A1,…, A25, B1,…, B25, where Ai = 1 if the ith voter in bloc A votes in favor, and similarly for Bi, then C’s degree of responsibility drops to 1/26. Intuitively, changing bloc A from voting for the outcome to voting against is a much “bigger” change than changing C from voting for the outcome to voting against. The current definition does not reflect that (although I suspect people’s responsibility judgments do). ■
Example 3.5.1 captures a related phenomenon.
Example 6.3.2 Consider Example 3.5.1 again. Recall that, in this example, there is a team consisting of Alice, Bob, Chuck, and Dan. In order to compete in the International Salsa Tournament, the team must have at least one male and one female member. All four of the team members are supposed to show up for the competition, but in fact none of them does. To what extent is each of the team members responsible for the fact that the team could not compete?
The naive definition of responsibility says that all team members have degree of responsibility 1/2. For example, if Alice shows up, then each of Bob, Chuck, and Dan becomes critical. However, there is an intuition that Alice is more responsible for the outcome than any of Bob, Chuck, or Dan. Intuitively, there are three ways for Alice to be critical: if any of Bob, Chuck, or Dan show up. But there is only one way for Dan to be critical: if Alice shows up. Similarly for Bob and Chuck. ■
Recall that in Chapter 3, the alternative definition of normality took into account the fact that there were more witnesses for Alice being a cause of the team not being able to participate than for each of Bob, Chuck, or Dan, and ended up grading Alice a “better” cause. It is not hard to modify Definitions 6.1.1 and 6.1.6 to also take this into account. For example, in Definition 6.1.1, we could count not just the size of the minimal witness set but the number of witness sets of that size. Indeed, we could take into account how many witness sets there are of each size. (See the notes at the end of the chapter for an explicit approach to doing this.)
This example also suggests a connection between responsibility and normality. Thinking in terms of normality could help explain why changing the votes of an entire bloc of voters in Example 6.3.1 is viewed as having a bigger impact than just changing the vote of one voter: we can think of changing the votes of an entire bloc of voters as being a more abnormal change than just changing the vote of a single voter.
The connection between normality and responsibility seems to run deep. The next example provides another illustration of the phenomenon.
Example 6.3.3 Suppose that there are five people on a congressional committee. Three votes are required for a measure to pass the committee. A, B, and C vote against the procedure, while D and E vote for it, so the measure fails. Each of A, B, and C is a cause of the measure failing, and thus have degree of responsibility 1. But now suppose that A is a Democrat, whereas B and C are Republicans. Moreover, the Democratic party favors the measure and the Republican party is opposed to it. Does that change things? For most people, it does. Going back to graded causality, A would be viewed as a “better” cause of the outcome than B because the witness world where A votes for the measure is more normal than the world where B votes for the measure. Sure enough, people do assign A more responsibility for the outcome than either B or C. This suggests that people do seem to be taking normality considerations into account when ascribing degree of responsibility. ■
Gerstenberg, Halpern, and Tenenbaum did an extensive series of experiments on voting behavior of the type discussed in Example 6.3.3. The number of committee members was always either 3 or 5. They varied the number of votes required for the measure to pass, the party affiliations of the committee members, and whether the parties supported the measure or opposed it. As expected, pivotality considerations, that is, how far a voter was from being critical to the outcome, in the sense captured by Definitions 6.1.1 and 6.1.6, were highly correlated with the outcome. Normality considerations also affected the outcome. The normality considerations came in two flavors. First, voting against your party was considered abnormal, as suggested in Example 6.3.3. But this does not completely explain the observations. In the causal setting discussed in Example 6.3.3, when all voters should have responsibility 1 according to the definition, in fact, the average degree of responsibility ascribed (averaged over subjects in the experiment) was about.75 to voter A and.5 to voter B.
We can get some insight into this phenomenon if we consider votes where party considerations do not apply. For example, suppose that there are three committee members, all in the same party, all three vote for a measure, and unanimity is needed for the measure to pass. This means that all three voters are but-for causes of the outcome and should have degree of responsibility 1 according to the naive definition. But again, subjects only assign them an average degree of responsibility of.75. Interestingly, if only one vote is needed for the measure to pass and only one committee member votes for it, then that committee member gets an average degree of responsibility very close 1. So somehow responsibility is being diffused even when everyone who voted for the measure is a but-for cause.
One way of understanding this is by considering a different normality criterion. Note that if only one vote is needed for the measure to pass, there are three voters, and the vote is 2–1 against, then the voter who voted in favor is “bucking the trend” and acting more abnormally than in the case where all three voters voted for the measure and three votes are needed to pass it. Thus, the difference between the two assignments of responsibility can be understood in terms of normality considerations if we identify degree of normality with “degree of going along with the crowd”.
Taking normality into account also lets us account for another phenomenon that we see with responsibility attributions: they typically attenuate over a long chain. Recall the example from Section 3.4.4, where a lit match aboard a ship caused a cask of rum to ignite, causing the ship to burn, which resulted in a large financial loss by Lloyd’s insurance, leading to the suicide of a financially ruined insurance executive. Although each of the events along the causal path from the lit match to the suicide is a (but-for) case of the suicide, as we saw in Section 3.4.4, a reasonable normality ordering results in witnesses for causes further up the chain being viewed as less normal than the witnesses for causes closer to the suicide, so the graded notion of normality deals with this well, at least for the original and modified and updated definition. By incorporating these normality considerations into the notion of responsibility, responsibility will also attenuate along causal chains, at least with the original and updated definition. (I discuss another approach to dealing with this problem, based on the observations in Example 6.2.7, shortly.)
I now sketch one way of incorporating normality considerations more formally into the notion of degree of responsibility The idea is to consider the normality of the changes required to move from the actual world to a witness world. Going back to the naive definition of responsibility, suppose that we start in a context ![[image]](images/eqn1158.jpg) . Changing the value of a variable from its value in
. Changing the value of a variable from its value in ![[image]](images/eqn1159.jpg) or holding a variable fixed at a value inconsistent with other changes is, all else being equal, abnormal, but not all changes or clampings of variables are equally abnormal. Changing the votes of a large bloc of voters is more abnormal, in general, than changing the vote of one voter; changing a vote so that it is more aligned with the majority is less abnormal than changing it to be less aligned with the majority; changing the vote of a voter so that it is more aligned with his party’s views is more normal than changing it so that it is less aligned with his party’s view; and so on. We would expect the degree of responsibility to be inversely related to the “difficulty” of getting from the actual world to the witness, where the difficulty depends on both the “distance” (i.e., how many changes have to be made to convert the actual world to the witness world—that is what is being measured by the naive definition of responsibility) and how normal these changes are—the larger the increase in normality (or the smaller the decrease in normality), the shorter the distance, and hence the greater the responsibility.
or holding a variable fixed at a value inconsistent with other changes is, all else being equal, abnormal, but not all changes or clampings of variables are equally abnormal. Changing the votes of a large bloc of voters is more abnormal, in general, than changing the vote of one voter; changing a vote so that it is more aligned with the majority is less abnormal than changing it to be less aligned with the majority; changing the vote of a voter so that it is more aligned with his party’s views is more normal than changing it so that it is less aligned with his party’s view; and so on. We would expect the degree of responsibility to be inversely related to the “difficulty” of getting from the actual world to the witness, where the difficulty depends on both the “distance” (i.e., how many changes have to be made to convert the actual world to the witness world—that is what is being measured by the naive definition of responsibility) and how normal these changes are—the larger the increase in normality (or the smaller the decrease in normality), the shorter the distance, and hence the greater the responsibility.
An important point here is that when we judge the abnormality of a change, we do so from the perspective of the event whose responsibility we are judging. The following example should help clarify this.
Example 6.3.4 Recall that in Example 3.5.2, A flips a switch, followed by B (who knows A’s choice). If they both flip the switch in the same direction, C gets a shock. In the actual context, B wants to shock C, so when A flips the switch to the right, so does B, and C gets a shock. We now want to consider the extent to which A and B are responsible for C’s shock. In the witness showing that A is responsible, A’s flip has to change from left to right and B’s flip has to be held constant. Given that B wants to shock C, holding B’s flip constant is quite abnormal. Now it is true that wanting to shock someone is abnormal from the point of view of societal norms, but since A doesn’t want to shock C, this norm is not relevant when judging A’s responsibility. By way of contrast, society’s norms are quite relevant when it comes to judging B’s responsibility. For B to be responsible, the witness world is one where B’s flip changes (and A’s flip stays the same as it is in the actual context). Although it is abnormal to change B’s flip in the sense that doing so goes against B’s intent, it makes for a more normal outcome according to society’s norms. The net effect is to make B’s change not so large. The move from the actual world to the witness world for A being a cause results in a significant decrease in normality; the move from the actual world to the witness world for B being a cause results in a much smaller decrease in normality (or perhaps even an increase). Thus, we judge B to be more responsible. Similar considerations apply when considering Billy’s medical condition (see the discussion in Example 3.5.2).
Note that these considerations are similar to those used when applying ideas of normality to judge causality, provided that we do not just look at the normality of the witness worlds involved but rather consider the normality of the changes involved in moving from the actual world to the witness world, relative to the event we are interested in. ■
One final confounding factor when it comes to responsibility judgments is that, as I said earlier, people seem to conflate responsibility and blame, as I have defined them. Recall the discussion of the bystander effect in Example 6.2.8. Suppose people are asked to what degree a bystander is responsible for the victim’s death if there are n bystanders, none of whom acted. We would expect that the larger n is, the lower the degree of responsibility assigned to each bystander. Part of this can be explained by the normality effect just discussed. The more bystanders there are doing nothing, the more abnormal it is for someone to act (in some sense of the word “abnormal”), so the lower the degree of responsibility for each one. But it may also be that when asked about the degree of responsibility of a bystander, people are actually responding with something like the degree of blame. As we have already seen, under some reasonable assumptions, the degree of blame goes down as n increases.
Thinking in terms of blame also provides an approach to dealing with the apparent attenuation of responsibility along causal chains, namely, the claim is that what is attenuating is really blame (in the technical sense that I have defined it in Section 6.2), not responsibility. As I pointed out in the discussion in Example 6.2.7, for all variants of the HP definition, the degree of blame attenuates as we go along the chain.
This discussion suggests that we may want to combine considerations of normality and blame. The alternative approach to incorporating normality given in Section 3.5 gives us a useful framework for doing so, especially when combined with some of the ideas in Chapter 5. In the alternative approach to normality, I assume a partial preorder on contexts that is viewed as a normality ordering. For blame, I assumed a probability on contexts in this section, but that was mainly so that we could compute blame as the expected degree of responsibility. I discussed in Sections 5.2.1 and 5.5.1 how a partial preorder on worlds can be viewed as algebraic conditional plausibility measure. Recall that an algebraic plausibility measure is just a generalization of probability: it is a function that associates with each event (set of worlds) a plausibility, and it has operations ⊕ and ⊗ that are analogues of addition and multiplication, so that plausibilities can be added and multiplied. If we also take the degree of responsibility to be an element of the domain of the plausibility measure, we can still take blame to be the expected degree of responsibility, but now it can be a more qualitative plausibility, rather than necessarily being a number. This is perhaps more consistent with the more qualitative way people use and assign blame. In any case, this viewpoint lets us work with blame and normality in one framework; instead of using probability or an partial preorder on worlds, we use a plausibility measure (or perhaps two plausibility measures: one representing likelihood and the other representing normality in the sense of norms). Doing this also lets us incorporate normality considerations into blame in a natural way and lets us work with likelihood without necessarily requiring a probabilistic representation of it. It is not yet clear how much is gained by this added generalization, although it seems worth exploring.
The definitions of responsibility and blame given in Sections 6.1 and 6.2 are largely taken from [Chockler and Halpern 2004], as is much of the discussion in these sections. However, there is a subtle difference between the definition of responsibility given here for the original and updated definition and the one given by Chockler and Halpern. In computing the degree of responsibility of X = x for φ, the Chockler-Halpern definition counted the number of changes needed to make X = x critical. Thus, for example, in Example 6.1.4, it would have taken the degree of responsibility of A = 0 for C = 1 to be 1, since the value of B did not have to change to make A = 0 critical. Similarly, it would take Suzy’s throw in the sophisticated rock-throwing model to be 1. The current definition seems to be a more accurate representation of people’s responsibility ascriptions.
The definition of blame given here is also slightly modified from the original Chockler- Halpern definition. Here I assume that all the contexts ![[image]](images/eqn1160.jpg) in the set
in the set ![[image]](images/eqn1161.jpg) used to assign a degree of blame to
used to assign a degree of blame to ![[image]](images/eqn1162.jpg) also satisfy
also satisfy ![[image]](images/eqn1163.jpg) . In [Chockler and Halpern 2004], it was assumed that the contexts in
. In [Chockler and Halpern 2004], it was assumed that the contexts in ![[image]](images/eqn1164.jpg) represented the agent’s epistemic state prior to observing
represented the agent’s epistemic state prior to observing ![[image]](images/eqn1165.jpg) , and the degree of responsibility of
, and the degree of responsibility of ![[image]](images/eqn1166.jpg) for φ was computed with respect to
for φ was computed with respect to ![[image]](images/eqn1167.jpg) , not
, not ![[image]](images/eqn1168.jpg) . The choice here is arguably more reasonable, given that my focus has been on assigning degree of blame and responsibility to
. The choice here is arguably more reasonable, given that my focus has been on assigning degree of blame and responsibility to ![[image]](images/eqn1169.jpg) in circumstances where
in circumstances where ![[image]](images/eqn1170.jpg) holds. Note that the agent might well assign different probabilities to settings if
holds. Note that the agent might well assign different probabilities to settings if ![[image]](images/eqn1171.jpg) is observed than if
is observed than if ![[image]](images/eqn1172.jpg) is the result of an intervention setting
is the result of an intervention setting ![[image]](images/eqn1173.jpg) to
to ![[image]](images/eqn1174.jpg) .
.
There is an analysis of the complexity of computing the degree of responsibility and blame for the original HP definition by Chockler and Halpern [2004], for the updated definition by Aleksandrowicz et al. [2014], and for the modified definition by Alechina, Halpern, and Logan [2016].
Tim Williamson [private communication, 2002] suggested the marksmen example to distinguish responsibility from blame. The law apparently would hold the marksmen who fired the live bullet more accountable than the ones who fired blanks. To me, this just says that the law is taking into account both blame and responsibility when it comes to punishment. I think there are advantages to carefully distinguishing what I have called “blame” and “responsibility” here, so that we can then have a sensible discussion of how punishment should depend on each.
Zimmerman [1988] gives a good introduction to the literature on moral responsibility. Somewhat surprisingly, most of the discussion of moral responsibility in the literature does not directly relate moral responsibility to causality. Shafer [2001] does discuss a notion of responsibility that seems somewhat in the spirit of the notion of blame as defined here, especially in that he views responsibility as being based (in part) on causality. However, he does not give a formal definition of responsibility, so it is hard to compare his notion to the one used here. Moreover, there are some significant technical differences between his notion of causality and the HP definition, so a formalization of Shafer’s notion would undoubtedly be different from the notions used here.
Hart and Honoré [1985, p. 482] discuss how different epistemic states are relevant for determining responsibility.
Goldman [1999] seems to have been the first to explain voting in terms of (causal) responsibility. His analysis was carried out in terms of Mackie’s INUS condition (see the notes to Chapter 1), but essentially the same analysis applies here. He also raised the point that someone who abstains should have a smaller degree of responsibility for an outcome than someone who votes for it, but did not show formally that this was the case in his model. Riker and Ordeshook [1968] estimated the probability of a voter being decisive in a U.S. presidential election as 10−8.
Gerstenberg and Lagnado [2010] showed that the notion of responsibility defined here does a reasonable job in characterizing people’s causality ascriptions. Zultan, Gerstenberg, and Lagnado [2012] discuss the effect of multiple witnesses on responsibility ascriptions and give Example 3.5.1 as an instance of this phenomenon. They also provide a formal definition of responsibility that takes this into account. Given X = x, φ, and a causal setting (M, u), let
![[image]](images/eqn1175.jpg)
where k is the number of witnesses for X = x being a cause of φ, and for each witness (![[image]](images/eqn1176.jpg) ,
, ![[image]](images/eqn1177.jpg) , xi),
, xi), ![[image]](images/eqn1178.jpg) , for i = 1,…, k. Then the degree of responsibility is taken to be 1/(N + 1). In the special case where there is only one witness, this definition reduces to Definition 6.1.1. Zultan, Gerstenberg, and Lagnado show this more refined notion of responsibility is a better predictor of people’s ratings than the one given by Definition 6.1.1.
, for i = 1,…, k. Then the degree of responsibility is taken to be 1/(N + 1). In the special case where there is only one witness, this definition reduces to Definition 6.1.1. Zultan, Gerstenberg, and Lagnado show this more refined notion of responsibility is a better predictor of people’s ratings than the one given by Definition 6.1.1.
The voting experiments discussed in Section 6.3 are described in [Gerstenberg, Halpern, and Tenenbaum 2015]. There it is pointed out that, in addition to pivotality and normality, what is called criticality is significant. The notion of criticality used is discussed in more detail by Lagnado, Gerstenberg, and Zultan [2013]. Criticality is meant to take people’s prior beliefs into account. Taking Pr to be the prior probability on causal settings, Lagnado, Gerstenberg, and Zultan characterize the criticality of X = x for φ by the formula
![[image]](images/eqn1179.jpg)
X = x is assumed to have a positive impact on φ, so Pr(φ | X = x) > Pr(φ | X ≠ x). If X = x is irrelevant to φ, then Pr(φ | X = x) = Pr(φ | X ≠ x) so Crit (φ, X = x) = 0. However, if X = x is necessary for φ, then Pr(φ | X ≠ x) = 1 so Crit (φ, X = x) = 1. Lagnado, Gerstenberg, and Zultan then suggest that the ascription of responsibility is some function of criticality and pivotality.
I have not discussed criticality here because I view it as playing essentially the same role as blame. Note that if X = x is irrelevant to φ, then the degree of blame of X = x for φ is 0; if X = x is necessary for φ in the sense of being a but-for cause of φ whenever φ occurs, and φ is known to have occurred (i.e., φ holds in all causal setting in ![[image]](images/eqn1180.jpg) ), then the degree of blame of X = x for φ is 1. Although the degree of blame and degree of criticality are related, and both take prior probabilities into account, they are not the same. For example, if X = x and φ are perfectly correlated, but X = x is not a cause of φ (which would be the case if X = x and φ have a common cause), then the degree of blame of X = x for φ would be 0, whereas Crit (φ, X = x) would still be 1. It seems to me that degree of blame comes closer to describing the impact of the prior probability on responsibility ascriptions than criticality in cases like this. But there is no question that, because people seem to conflate blame and responsibility, the prior probability will have an impact.
), then the degree of blame of X = x for φ is 1. Although the degree of blame and degree of criticality are related, and both take prior probabilities into account, they are not the same. For example, if X = x and φ are perfectly correlated, but X = x is not a cause of φ (which would be the case if X = x and φ have a common cause), then the degree of blame of X = x for φ would be 0, whereas Crit (φ, X = x) would still be 1. It seems to me that degree of blame comes closer to describing the impact of the prior probability on responsibility ascriptions than criticality in cases like this. But there is no question that, because people seem to conflate blame and responsibility, the prior probability will have an impact.
Further support for the role of normality in responsibility judgments is provided by the work of Kominsky et al. [2014] (although they present a somewhat different account of their experimental results than that given here).
See Chu and Halpern [2008] for details on applying plausibility measures in the context of expectation.
Explanation
Good explanations are like bathing suits, darling; they are meant to reveal everything by covering only what is necessary.
E. L. Konigsburg
There has to be a mathematical explanation for how bad that tie is.
Russell Crowe
Perhaps the main reason that people are interested in causality is that they want explanations. Consider the three questions I asked in the first paragraph of this book: Why is my friend depressed? Why won’t that file display properly on my computer? Why are the bees suddenly dying? The questions are asking for causes; the answers would provide an explanation.
Perhaps not surprisingly, just as with causality, getting a good definition of explanation is notoriously difficult. And, just as with causality, issues concerning explanation have been the focus of philosophical investigation for millennia. In this chapter, I show how the ideas behind the HP definition of causality can be used to give a definition of (causal) explanation that deals well with many of the problematic examples discussed in the literature. The basic idea is that an explanation is a fact that, if found to be true, would constitute an actual cause of the explanandum (the fact to be explained), regardless of the agent’s initial uncertainty.
As this gloss suggests, the definition of explanation involves both causality and knowledge. What counts as an explanation for one agent may not count as an explanation for another agent, since the two agents may have different epistemic states. For example, an agent seeking an explanation of why Mr. Johansson has been taken ill with lung cancer will not consider the fact that he worked for years in asbestos manufacturing a part of an explanation if he already knew this fact. For such an agent, an explanation of Mr. Johansson’s illness may include a causal model describing the connection between asbestos fibers and lung cancer. However, for someone who already knows the causal model but does not know that Mr. Johansson worked in asbestos manufacturing, the explanation would involve Mr. Johansson’s employment but would not mention the causal model. This example illustrates another important point: an explanation may include (fragments of) a causal model.
Salmon distinguishes between epistemic and ontic explanations. Roughly speaking, an epistemic explanation is one that depends on an agent’s epistemic state, telling him something that he doesn’t already know, whereas an ontic explanation is agent-independent. An ontic explanation would involve the causal model and all the relevant facts. When an agent asks for an explanation, he is typically looking for an epistemic explanation relative to his epistemic state; that is, those aspects of the ontic explanation that he does not already know. Both notions of explanation seem to me to be interesting. Moreover, having a good definition of one should take us a long way toward getting a good definition of the other. The definitions I give here are more in the spirit of the epistemic notion.
7.1 Explanation: The Basic Definition
The “classical” approaches to defining explanation in the philosophy literature, such as Hempel’s deductive-nomological model and Salmon’s statistical relevance model, fail to exhibit the directionality inherent in common explanations. Despite all the examples in the philosophy literature on the need for taking causality and counterfactuals into account, and the extensive work on causality defined in terms of counterfactuals in the philosophy literature, philosophers have been reluctant to build a theory of explanation on top of a theory of causality built on counterfactuals. (See the notes at the end of the chapter.)
As I suggested above, the definition of explanation is relative to an epistemic state, just like that of blame. An epistemic state ![[image]](images/eqn1181.jpg) , as defined in Section 6.2, is a set of causal settings, with a probability distribution over them. I assume for simplicity in the basic definition that the causal model is known, so that we can view an epistemic state as a set of contexts. The probability distribution plays no role in the basic definition, although it will play a role in the next section, when I talk about the “quality” or “goodness” of an explanation. Thus, for the purposes of the following definition, I take an epistemic state to simply be a set
, as defined in Section 6.2, is a set of causal settings, with a probability distribution over them. I assume for simplicity in the basic definition that the causal model is known, so that we can view an epistemic state as a set of contexts. The probability distribution plays no role in the basic definition, although it will play a role in the next section, when I talk about the “quality” or “goodness” of an explanation. Thus, for the purposes of the following definition, I take an epistemic state to simply be a set ![[image]](images/eqn1182.jpg) of contexts. I think of
of contexts. I think of ![[image]](images/eqn1183.jpg) as the set of contexts that the agent considers possible before observing φ, the explanandum. Given a formula ψ, let
as the set of contexts that the agent considers possible before observing φ, the explanandum. Given a formula ψ, let ![[image]](images/eqn1184.jpg) . Recall that in Section 3.5, I defined
. Recall that in Section 3.5, I defined ![[image]](images/eqn1185.jpg) . Using this notation (which will be useful later in this chapter),
. Using this notation (which will be useful later in this chapter), ![[image]](images/eqn1186.jpg) .
.
The definition of explanation is built on the definition of sufficient causality, as defined in Section 2.6. Just as there are three variants of the definition of causality, there are three variants of the definition of explanation.
Definition 7.1.1 ![[image]](images/eqn1187.jpg) is an explanation of φ relative to a set
is an explanation of φ relative to a set ![[image]](images/eqn1188.jpg) of contexts in a causal model M if the following conditions hold:
of contexts in a causal model M if the following conditions hold:
EX1. ![[image]](images/eqn1189.jpg) is a sufficient cause of φ in all contexts in
is a sufficient cause of φ in all contexts in ![[image]](images/eqn1190.jpg) satisfying
satisfying ![[image]](images/eqn1191.jpg) . More precisely,
. More precisely,
![[image]](images/eqn1192.jpg) and
and ![[image]](images/eqn1193.jpg) , then there exists a conjunct X = x of
, then there exists a conjunct X = x of ![[image]](images/eqn1194.jpg) and a (possibly empty) conjunction
and a (possibly empty) conjunction ![[image]](images/eqn1195.jpg) such that
such that ![[image]](images/eqn1196.jpg) is a cause of φ in (M,
is a cause of φ in (M, ![[image]](images/eqn1197.jpg) ). (This is essentially condition SC2 from the definition of sufficient cause, applied to all contexts
). (This is essentially condition SC2 from the definition of sufficient cause, applied to all contexts ![[image]](images/eqn1198.jpg) . Note that SC1 is guaranteed to hold in all contexts in
. Note that SC1 is guaranteed to hold in all contexts in ![[image]](images/eqn1199.jpg) .)
.)![[image]](images/eqn1200.jpg) for all contexts
for all contexts ![[image]](images/eqn1201.jpg) . (This is just the sufficiency condition SC3, restricted to the contexts in
. (This is just the sufficiency condition SC3, restricted to the contexts in ![[image]](images/eqn1202.jpg) .)
.)EX2. ![[image]](images/eqn1203.jpg) is minimal; there is no strict subset
is minimal; there is no strict subset ![[image]](images/eqn1204.jpg) of
of ![[image]](images/eqn1205.jpg) such that
such that ![[image]](images/eqn1206.jpg) satisfies EX1, where
satisfies EX1, where ![[image]](images/eqn1207.jpg) is the restriction of
is the restriction of ![[image]](images/eqn1208.jpg) to the variables in
to the variables in ![[image]](images/eqn1209.jpg) . (This is just SC4.)
. (This is just SC4.)
EX3. ![[image]](images/eqn1210.jpg) . (This just says that the agent considers possible a context where the explanation holds.) ■
. (This just says that the agent considers possible a context where the explanation holds.) ■
The explanation is nontrivial if it satisfies in addition
EX4. ![[image]](images/eqn1211.jpg) for some
for some ![[image]](images/eqn1212.jpg) (The explanation is not already known given the observation of φ.) ■
(The explanation is not already known given the observation of φ.) ■
Most of the conditions here depend only on ![[image]](images/eqn1213.jpg) , the set of contexts that the agent considers possible after discovering φ. The set
, the set of contexts that the agent considers possible after discovering φ. The set ![[image]](images/eqn1214.jpg) plays a role only in the second clause of EX1 (the analogue of SC3); it determines the set of contexts for which the condition
plays a role only in the second clause of EX1 (the analogue of SC3); it determines the set of contexts for which the condition ![[image]](images/eqn1215.jpg) must hold.
must hold.
The minimality requirement EX2 essentially throws out parts of the explanation that are already known. Thus, we do not get an ontic explanation. The nontriviality requirement EX4 (which I view as optional) says that explanations that are known do not count as “real” explanations—the minimality requirement as written does not suffice to get rid of trivial explanations. This seems reasonable for epistemic explanations.
EX4 may seem incompatible with linguistic usage. For example, say that someone observes φ, then discovers some fact A and says, “Aha! That explains why φ happened.” That seems like a perfectly reasonable utterance, yet A is known to the agent when he says it. A is a trivial explanation of φ (one not satisfying EX4) relative to the epistemic state after A has been discovered. I think of ![[image]](images/eqn1216.jpg) as the agent’s epistemic state just after φ is discovered but before A is discovered (although nothing in the formal definition requires this). A may well be a nontrivial explanation of φ relative to the epistemic state before A was discovered. Moreover, even after an agent discovers A, she may still be uncertain about how A caused φ; that is, she may be uncertain about the causal model. This means that A is not, in fact, a trivial explanation once we take all of the agent’s uncertainty into account, as the more general definition of explanation will do.
as the agent’s epistemic state just after φ is discovered but before A is discovered (although nothing in the formal definition requires this). A may well be a nontrivial explanation of φ relative to the epistemic state before A was discovered. Moreover, even after an agent discovers A, she may still be uncertain about how A caused φ; that is, she may be uncertain about the causal model. This means that A is not, in fact, a trivial explanation once we take all of the agent’s uncertainty into account, as the more general definition of explanation will do.
Example 7.1.2 Consider again the forest-fire example (Example 2.3.1). In the notation introduced in Section 2.1, consider the following four contexts: in u0 = (0, 0), there is no lightning and no arsonist; in u1 = (1, 0), there is only lightning; in u2 = (0, 1), the arsonist drops a match but there is no lightning; and in u3 = (1, 1), there is lightning and the arsonist drops a match. In the disjunctive model Md, if ![[image]](images/eqn1217.jpg) , then both L = 1 and MD = 1 are explanations of FF = 1 relative to
, then both L = 1 and MD = 1 are explanations of FF = 1 relative to ![[image]](images/eqn1218.jpg) , according to all variants of the HP definition.
, according to all variants of the HP definition.
Going on with the example, L = 1 and MD = 1 are also both explanations of FF = 1 relative to ![[image]](images/eqn1219.jpg) and
and ![[image]](images/eqn1220.jpg) . However, in the case of
. However, in the case of ![[image]](images/eqn1221.jpg) , L = 1 is a trivial explanation; it is known once the forest fire is discovered.
, L = 1 is a trivial explanation; it is known once the forest fire is discovered.
By way of contrast, in the conjunctive forest-fire model Mc, relative to ![[image]](images/eqn1222.jpg) , the only explanation of the fire is L = 1 ∧ MD = 1. Due to the sufficiency requirement, with u0, u1, and u2 in
, the only explanation of the fire is L = 1 ∧ MD = 1. Due to the sufficiency requirement, with u0, u1, and u2 in ![[image]](images/eqn1223.jpg) , neither L = 1 nor MD = 1 is by itself an explanation of the fire. However, L = 1 MD = 1 is a trivial explanation. If the agent is convinced that the only way that the forest fire could start is through a combination of lightning and a dropped match (it could not, for example, have been due to unattended campfires), then once the forest fire is observed, he knows why it happened; he does not really need an explanation.
, neither L = 1 nor MD = 1 is by itself an explanation of the fire. However, L = 1 MD = 1 is a trivial explanation. If the agent is convinced that the only way that the forest fire could start is through a combination of lightning and a dropped match (it could not, for example, have been due to unattended campfires), then once the forest fire is observed, he knows why it happened; he does not really need an explanation.
However, with respect to ![[image]](images/eqn1224.jpg) , MD = 1 is an explanation of the forest fire, although a trivial one. Since L = 1 is already known, MD = 1 is all the agent needs to know to explain the fire, but since both MD = 1 and L = 1 are required for there to be a fire, the agent knows that MD = 1 when he see the fire. Note that MD = 1 ∧ L = 1 is not an explanation; it violates the minimality condition EX2. L = 1 is not an explanation either, since (Mc, u1) ⊨ ¬[L ← 1](FF = 1), so sufficient causality does not hold. ■
, MD = 1 is an explanation of the forest fire, although a trivial one. Since L = 1 is already known, MD = 1 is all the agent needs to know to explain the fire, but since both MD = 1 and L = 1 are required for there to be a fire, the agent knows that MD = 1 when he see the fire. Note that MD = 1 ∧ L = 1 is not an explanation; it violates the minimality condition EX2. L = 1 is not an explanation either, since (Mc, u1) ⊨ ¬[L ← 1](FF = 1), so sufficient causality does not hold. ■
This example already suggests why we want to consider sufficient causality in the context of explanation. We would not typically accept lightning as an explanation of the forest fire relative to either ![[image]](images/eqn1225.jpg) or
or ![[image]](images/eqn1226.jpg) .
.
Example 7.1.3 Now consider the voting scenario with 11 voters discussed in Section 2.1. Let ![[image]](images/eqn1227.jpg) consist of all the 211 contexts describing the possible voting patterns. If we want an explanation of why Suzy won relative to
consist of all the 211 contexts describing the possible voting patterns. If we want an explanation of why Suzy won relative to ![[image]](images/eqn1228.jpg) , then any subset of six voters voting for Suzy is one. Thus, in this case, the explanations look like the causes according to the modified HP definition. But this is not the case in general, as shown by the discussion above for the disjunctive model of the forest fire. If
, then any subset of six voters voting for Suzy is one. Thus, in this case, the explanations look like the causes according to the modified HP definition. But this is not the case in general, as shown by the discussion above for the disjunctive model of the forest fire. If ![[image]](images/eqn1229.jpg) consists of all the 26 contexts where voters 1 to 5 vote for Suzy, then each of Vi = 1 is an explanation of Suzy’s victory, for i = 6,…, 11. Intuitively, if we already know that the first five voters voted for Suzy, then a good explanation tells us who gave her the sixth vote. ■
consists of all the 26 contexts where voters 1 to 5 vote for Suzy, then each of Vi = 1 is an explanation of Suzy’s victory, for i = 6,…, 11. Intuitively, if we already know that the first five voters voted for Suzy, then a good explanation tells us who gave her the sixth vote. ■
Although I have used the word “explanation”, the explanations here should be thought of as potential or possible explanations. For example, when considering the explanation for Suzy’s victory relative to ![[image]](images/eqn1230.jpg) , where it is known that voters 1 to 5 voted for Suzy, calling voter 6 an explanation doesn’t mean that, in fact, voter 6 voted for Suzy. Rather, it means that it is possible that voter 6 voted for Suzy and, if she did, then her vote was sufficient to give Suzy the victory.
, where it is known that voters 1 to 5 voted for Suzy, calling voter 6 an explanation doesn’t mean that, in fact, voter 6 voted for Suzy. Rather, it means that it is possible that voter 6 voted for Suzy and, if she did, then her vote was sufficient to give Suzy the victory.
As with causes, Definition 7.1.1 disallows disjunctive explanations. However, disjunctive explanations seem to make perfect sense here, particularly since we are thinking in terms of possible explanations. It seems quite reasonable to say that Suzy’s victory is explained by the fact that either voter 6 or voter 7 or … voter 11 voted for her; we need further investigation to determine which voter it actually was. In this case, we can give a reasonable definition of disjunctive explanations; say that ![[image]](images/eqn1231.jpg) is an explanation of φ if each of
is an explanation of φ if each of ![[image]](images/eqn1232.jpg) is an explanation of φ, according to Definition 7.1.1. Disjunctive explanations defined in this way play a role when it comes to talking about the quality of an explanation, a point I return to in the next section. I conclude this section with one more example.
is an explanation of φ, according to Definition 7.1.1. Disjunctive explanations defined in this way play a role when it comes to talking about the quality of an explanation, a point I return to in the next section. I conclude this section with one more example.
Example 7.1.4 Suppose that there was a heavy rain in April and electrical storms in the following two months; and in June there was a forest fire. If it hadn’t been for the heavy rain in April, given the electrical storm in May, the forest would have caught fire in May (and not in June). However, given the storm, if there had been an electrical storm only in May, the forest would not have caught fire at all; if there had been an electrical storm only in June, it would have caught fire in June. The situation can be captured using a model with five endogenous binary variables:
The equations are straightforward: the value of AS, ESJ, and ESM is determined by the context; FFM = 1 exactly if ESM = 1 and AS = 0; FFJ = 1 exactly if ESJ = 1 and either AS = 1 or ESM = 0 (or both).
Identifying a context with a triple (i, j, k) consisting of the values of AS, ESM, and ESJ, respectively, let ![[image]](images/eqn1233.jpg) consist of all eight possible contexts. What are the explanations of the forest fire (FFM = 1∨FFJ = 1) relative to
consist of all eight possible contexts. What are the explanations of the forest fire (FFM = 1∨FFJ = 1) relative to ![[image]](images/eqn1234.jpg) ? It is easy to see that the only sufficient causes of fire are ESJ = 1 and ESM = 1 ∧ AS = 0, and these are in fact the only explanations of the fire relative to
? It is easy to see that the only sufficient causes of fire are ESJ = 1 and ESM = 1 ∧ AS = 0, and these are in fact the only explanations of the fire relative to ![[image]](images/eqn1235.jpg) . If we are instead interested in an explanation of a fire in June (FFJ = 1), then the only explanations are AS = 1∧ES J = 1 and ES M = 0∧ES J = 1. All the variants of the HP definition agree in these cases.
. If we are instead interested in an explanation of a fire in June (FFJ = 1), then the only explanations are AS = 1∧ES J = 1 and ES M = 0∧ES J = 1. All the variants of the HP definition agree in these cases.
This seems to me quite reasonable. The fact that there was a storm in June does not explain the fire in June, but the storm in June combined with either the fact that there was no storm in May or the fact that there were April showers does provide an explanation. It also seems reasonable to consider the disjunctive explanation (ES J = 1∧AS = 1) ∨ (ES J = 1 ∧ ES M = 0).
Now suppose that the agent already knows that there was a forest fire, so is seeking an explanation of the fire with respect to ![[image]](images/eqn1236.jpg) , the set consisting of the five contexts compatible with a fire, namely, (0, 1, 0), (0, 0, 1), (0, 1, 1), (1, 0, 1), and (1, 1, 1). In this case, the situation is a bit more complicated. The sufficient causality clause holds almost trivially, since there is a forest fire in all contexts under consideration. Here is a summary of the situation:
, the set consisting of the five contexts compatible with a fire, namely, (0, 1, 0), (0, 0, 1), (0, 1, 1), (1, 0, 1), and (1, 1, 1). In this case, the situation is a bit more complicated. The sufficient causality clause holds almost trivially, since there is a forest fire in all contexts under consideration. Here is a summary of the situation:
![[image]](images/eqn1237.jpg) according to the original HP definition.
according to the original HP definition.![[image]](images/eqn1238.jpg) according to all the variants of the HP definition. It is not hard to check that ES J = 1 is a cause of FF M = 1 ∨ FFJ = 1 in (M, u) for all contexts
according to all the variants of the HP definition. It is not hard to check that ES J = 1 is a cause of FF M = 1 ∨ FFJ = 1 in (M, u) for all contexts ![[image]](images/eqn1239.jpg) such that
such that ![[image]](images/eqn1240.jpg) according to the original and updated HP definition, and is part of a cause in all these contexts according to the modified HP definition.
according to the original and updated HP definition, and is part of a cause in all these contexts according to the modified HP definition.![[image]](images/eqn1241.jpg) according to the updated and modified HP definitions but is an explanation according to the original HP definition. Consider the context (1, 1, 1). I leave it to the reader to check that taking
according to the updated and modified HP definitions but is an explanation according to the original HP definition. Consider the context (1, 1, 1). I leave it to the reader to check that taking ![[image]](images/eqn1242.jpg) and setting
and setting ![[image]](images/eqn1243.jpg) shows that the May storm is a cause of the fire according to the original HP definition, but this is not a witness in the case of the updated HP definition. (Again, the original HP definition is arguably giving an inappropriate answer in this case.)
shows that the May storm is a cause of the fire according to the original HP definition, but this is not a witness in the case of the updated HP definition. (Again, the original HP definition is arguably giving an inappropriate answer in this case.)![[image]](images/eqn1244.jpg) according to the updated and modified HP definition; a conjunct of ES M = 1 ∧ AS = 0, namely ES M = 1, is part of a cause of FF M = 1 ∨ FF J = 1 in every context satisfying ES M = 1 ∧ AS = 0. Moreover, the minimality condition EX2 is easily seen to hold (since neither ES M = 1 nor AS = 0 is an explanation, as we have seen).
according to the updated and modified HP definition; a conjunct of ES M = 1 ∧ AS = 0, namely ES M = 1, is part of a cause of FF M = 1 ∨ FF J = 1 in every context satisfying ES M = 1 ∧ AS = 0. Moreover, the minimality condition EX2 is easily seen to hold (since neither ES M = 1 nor AS = 0 is an explanation, as we have seen).Now suppose that we are looking for an explanation of the June fire relative to ![[image]](images/eqn1245.jpg) .
.
Thus, although we have different explanations of fire relative to ![[image]](images/eqn1246.jpg) and
and ![[image]](images/eqn1247.jpg) , the explanations of the June fire are the same. ■
, the explanations of the June fire are the same. ■
7.2 Partial Explanations and Explanatory Power
Not all explanations are considered equally good. There are different dimensions of “goodness”, such as simplicity, generality, and informativeness. I focus on one aspect of “goodness” here: likelihood (without meaning to suggest that the other aspects are unimportant!). To capture the likelihood of an explanation, it is useful to bring probability into the picture. Suppose that the agent has a probability Pr on the set ![[image]](images/eqn1248.jpg) of possible contexts. Recall that I think of
of possible contexts. Recall that I think of ![[image]](images/eqn1249.jpg) as the set of contexts that the agent considers possible before observing the explanandum φ; Pr can be thought of as the agent’s prior probability on
as the set of contexts that the agent considers possible before observing the explanandum φ; Pr can be thought of as the agent’s prior probability on ![[image]](images/eqn1250.jpg) . One obvious way of defining the goodness of
. One obvious way of defining the goodness of ![[image]](images/eqn1251.jpg) as an explanation of φ relative to
as an explanation of φ relative to ![[image]](images/eqn1252.jpg) is to consider the probability of the set of contexts where
is to consider the probability of the set of contexts where ![[image]](images/eqn1253.jpg) is true or, as has been more commonly done, to consider this probability conditional on φ.
is true or, as has been more commonly done, to consider this probability conditional on φ.
This is certainly a useful notion of goodness. For example, going back to the forest-fire example and taking the set of contexts to be ![[image]](images/eqn1254.jpg) , the agent may consider lightning more likely than an arsonist dropping a match. In this case, intuitively, we should consider L = 1 a better explanation of the fire than MD = 1; it has a higher probability of being the actual explanation than MD = 1. (What I have been calling an explanation of φ should really be viewed as a possible explanation of φ; this definition of goodness provides one way of evaluating the relative merits of a number of possible explanations of φ.) Of course, if we allow disjunctive explanations, then L = 1 ∨ MD = 1 is an even better explanation from this viewpoint; it has probability 1 conditional on observing the fire. But this already points to an issue. Intuitively, L = 1 ∨ MD = 1 is a less informative explanation. I would like to capture this intuition of “informativeness”, but before doing so, it is useful to take a detour and consider partial explanations. For most of the discussion that follows, I do not consider disjunctive explanations; I return to them at the end of the section.
, the agent may consider lightning more likely than an arsonist dropping a match. In this case, intuitively, we should consider L = 1 a better explanation of the fire than MD = 1; it has a higher probability of being the actual explanation than MD = 1. (What I have been calling an explanation of φ should really be viewed as a possible explanation of φ; this definition of goodness provides one way of evaluating the relative merits of a number of possible explanations of φ.) Of course, if we allow disjunctive explanations, then L = 1 ∨ MD = 1 is an even better explanation from this viewpoint; it has probability 1 conditional on observing the fire. But this already points to an issue. Intuitively, L = 1 ∨ MD = 1 is a less informative explanation. I would like to capture this intuition of “informativeness”, but before doing so, it is useful to take a detour and consider partial explanations. For most of the discussion that follows, I do not consider disjunctive explanations; I return to them at the end of the section.
Example 7.2.1 Suppose that I see that Victoria is tanned and I seek an explanation. The causal model includes the three variables “Victoria took a vacation in the Canary Islands”, “sunny in the Canary Islands”, and “went to a tanning salon”; a context assigns values to just these three variables. That means that there are eight contexts, depending on the values assigned to these three variables. Before seeing Victoria, I consider all eight of them possible. Victoria going to the Canaries is not an explanation of Victoria’s tan, for two reasons. First, Victoria going to the Canaries is not a sufficient cause of Victoria getting a tan. There are contexts where it is not sunny in the Canaries and Victoria does not go to the tanning salon; going to the Canaries in those contexts would not result in her being tanned. And even among contexts where Victoria is tanned and goes to the Canaries, going to the Canaries is not the cause of her getting the tan in the context where it is not sunny and she goes to the tanning salon, at least according to the modified and updated HP definitions. (According to the original HP definition, it is a cause; this example has the same structure as Example 2.8.1, where A does not load B’s gun, although B shoots. And just as with that example, the original HP seems to be giving an inappropriate causality ascription here. The problem can be resolved in the same way as Example 2.8.1, by adding an extra variable for “Victoria vacationed in a place that was sunny and warm”; then going to the Canaries is not a cause of Victoria’s tan even according to the original HP definition.) Nevertheless, most people would accept “Victoria took a vacation in the Canary Islands” as a satisfactory explanation of Victoria being tanned. Although EX1 is not satisfied, intuitively, it is “almost” satisfied, especially if we assume that the Canaries are likely to be sunny. The problematic contexts are exactly the ones where it is not sunny in the Canaries, and these have low probability. The only complete (ontic) explanations according to Definition 7.1.1 are “Victoria went to the Canary Islands and it was sunny”, “Victoria went to the Canary Islands and did not go to a tanning salon”, and “Victoria went to a tanning salon”. “Victoria went to the Canary Islands” is a partial explanation (a notion more general than just being part of an explanation). ■
In Example 7.2.1, the partial explanation can be extended to a complete explanation by adding a conjunct. But not every partial explanation as I am about to define it can be extended to a complete explanation. Roughly speaking, this is because the complete explanation may involve exogenous factors, which are not permitted in explanations. Suppose, for example, that we used a different causal model for Victoria, one where the only endogenous variable is the one representing Victoria’s vacation; there is no variable corresponding to the weather in the Canaries, nor one corresponding to whether Victoria goes to a tanning salon. Instead, the model simply has exogenous variables that can make Victoria suntanned even in the absence of a trip to the Canaries and leave her not suntanned even if she goes to the Canaries. Arguably this model is insufficiently expressive, since it does not capture important features of the story. But even in this model, Victoria’s vacation would still be a partial explanation of her suntan: the contexts where it fails to be a (sufficient) cause (ones corresponding to no sun in the Canary Islands) are fairly unlikely. But note that, in this model, we cannot add conjuncts to the event of Victoria going to the Canaries that exclude the “bad” contexts from consideration. Indeed, in this model, there is no (complete) explanation for Victoria’s tan. Given the choice of exogenous variables, it is inexplicable!
Intuitively, if we do not have a “name” for a potential cause, then there may not be an explanation for an observation. This type of situation arises often, as the following example shows.
Example 7.2.2 Suppose that the sound on a television works but there is no picture. Furthermore, the only cause of there being no picture that the agent is aware of is the picture tube being faulty. (Older non-digital televisions had picture tubes.) However, the agent is also aware that there are times when there is no picture even though the picture tube works perfectly well—intuitively, there is no picture “for inexplicable reasons”. This is captured by the causal network described in Figure 7.1, where T describes whether the picture tube is working (1 if it is and 0 if it is not) and P describes whether there is a picture (1 if there is and 0 if there is not). The exogenous variable U0 determines the status of the picture tube:
![[image]](images/fig7-1.jpg)
Figure 7.1: The television with no picture.
T = U0. The exogenous variable U1 is meant to represent the mysterious “other possible causes”. If U1 = 0, then whether there is a picture depends solely on the status of the picture tube—that is, P = T. However, if U1 = 1, then there is no picture (P = 0) no matter what the status of the picture tube. Thus, in contexts where U1 = 1, T = 0 is not a cause of P = 0. Now suppose that ![[image]](images/eqn1255.jpg) includes the contexts
includes the contexts ![[image]](images/eqn1256.jpg) , where U0 = U1 = 0, and
, where U0 = U1 = 0, and ![[image]](images/eqn1257.jpg) , where U0 = 1 and U1 = 0. The only cause of P = 0 in both
, where U0 = 1 and U1 = 0. The only cause of P = 0 in both ![[image]](images/eqn1258.jpg) and -
and -![[image]](images/eqn1259.jpg) is P = 0 itself (assuming that we do not exclude self-causation). (Note that T = 0 is not a cause of P = 0 in
is P = 0 itself (assuming that we do not exclude self-causation). (Note that T = 0 is not a cause of P = 0 in ![[image]](images/eqn1260.jpg) , since P = 0 even if T is set to 1.) Indeed, there is no nontrivial explanation of P = 0 relative to any epistemic state
, since P = 0 even if T is set to 1.) Indeed, there is no nontrivial explanation of P = 0 relative to any epistemic state ![[image]](images/eqn1260a.jpg) that includes
that includes ![[image]](images/eqn1261.jpg) and
and ![[image]](images/eqn1262.jpg) . However, T = 0 is a cause of P = 0 in all contexts in
. However, T = 0 is a cause of P = 0 in all contexts in ![[image]](images/eqn1263.jpg) satisfying T = 0 other than
satisfying T = 0 other than ![[image]](images/eqn1264.jpg) and is a sufficient cause of P = 0 in all contexts. If the probability of
and is a sufficient cause of P = 0 in all contexts. If the probability of ![[image]](images/eqn1265.jpg) is low (capturing the intuition that it is unlikely that more than one thing goes wrong with a television at once), then we are entitled to view T = 0 as a quite good partial explanation of P = 0 with respect to
is low (capturing the intuition that it is unlikely that more than one thing goes wrong with a television at once), then we are entitled to view T = 0 as a quite good partial explanation of P = 0 with respect to ![[image]](images/eqn1266.jpg) .
.
Note that if we modify the causal model by adding an endogenous variable, say I, corresponding to the “inexplicable” cause U1 (with equation I = U1), then T = 0 and I = 0 both become explanations of P = 0, according to all variants of the HP definition. ■
Example 7.2.2 and the discussion after Example 7.2.1 emphasize the point I made above: if there is no name for a cause, then there may be no explanation. Adding an endogenous variable that provides such a name can result in there being an explanation when there was none before. This phenomenon of adding “names” to create explanations is quite common. For example, “gods” are introduced to explain otherwise inexplicable phenomena; clusters of symptoms are given names in medicine so as to serve as explanations.
I now define partial explanation formally. The definition is now relative to a pair (![[image]](images/eqn1267.jpg) , Pr), just like the definition of blame. Once we have a probability distribution in the picture, it makes sense to modify conditions EX3 and EX4 so that they use the distribution. That is, EX3 would now say that
, Pr), just like the definition of blame. Once we have a probability distribution in the picture, it makes sense to modify conditions EX3 and EX4 so that they use the distribution. That is, EX3 would now say that ![[image]](images/eqn1268.jpg) , rather than just
, rather than just ![[image]](images/eqn1269.jpg) ; similarly, EX4 becomes
; similarly, EX4 becomes ![[image]](images/eqn1270.jpg) . I assume that the modified definition is applied whenever there is a probability in the picture.
. I assume that the modified definition is applied whenever there is a probability in the picture.
Definition 7.2.3 Given a set ![[image]](images/eqn1271.jpg) of contexts in a causal model M and a probability Pr on
of contexts in a causal model M and a probability Pr on ![[image]](images/eqn1272.jpg) , let
, let ![[image]](images/eqn1273.jpg) consist of all contexts
consist of all contexts ![[image]](images/eqn1274.jpg) that satisfy SC2 with respect to
that satisfy SC2 with respect to ![[image]](images/eqn1275.jpg) (i.e., the first condition in EX1). More precisely,
(i.e., the first condition in EX1). More precisely,
![[image]](images/eqn1276.jpg)
Let ![[image]](images/eqn1277.jpg) consist of all contexts
consist of all contexts ![[image]](images/eqn1278.jpg) that satisfy SC3; that is,
that satisfy SC3; that is,
![[image]](images/eqn1279.jpg)
![[image]](images/eqn1280.jpg) is a partial explanation of φ with goodness (α, β) relative to (
is a partial explanation of φ with goodness (α, β) relative to (![[image]](images/eqn1281.jpg) , Pr) if
, Pr) if ![[image]](images/eqn1282.jpg) is an explanation of φ relative to
is an explanation of φ relative to ![[image]](images/eqn1283.jpg) ,
, ![[image]](images/eqn1284.jpg) , and
, and ![[image]](images/eqn1285.jpg) . ■
. ■
The goodness of a partial explanation measures the extent to which it provides an explanation of φ. As I mentioned above, there are two ways that ![[image]](images/eqn1286.jpg) can fail to provide an explanation: there may be some contexts
can fail to provide an explanation: there may be some contexts ![[image]](images/eqn1287.jpg) that satisfy
that satisfy ![[image]](images/eqn1288.jpg) but
but ![[image]](images/eqn1289.jpg) is not a cause of φ in (M,
is not a cause of φ in (M, ![[image]](images/eqn1290.jpg) ) (these are the contexts in
) (these are the contexts in ![[image]](images/eqn1291.jpg) ), and there may be contexts where the sufficient causality condition
), and there may be contexts where the sufficient causality condition ![[image]](images/eqn1292.jpg) does not hold (these are the contexts in
does not hold (these are the contexts in ![[image]](images/eqn1293.jpg) . The parameter α in the definition of partial explanation measures the fraction of the contexts in
. The parameter α in the definition of partial explanation measures the fraction of the contexts in ![[image]](images/eqn1294.jpg) that are “good” in the first sense; the parameter β measures the fraction of contexts in
that are “good” in the first sense; the parameter β measures the fraction of contexts in ![[image]](images/eqn1295.jpg) that are good in the second sense. For the first sense of goodness, we care only about which contexts in
that are good in the second sense. For the first sense of goodness, we care only about which contexts in ![[image]](images/eqn1296.jpg) are good, so it makes sense to condition on
are good, so it makes sense to condition on ![[image]](images/eqn1297.jpg) . If
. If ![[image]](images/eqn1298.jpg) is an explanation of φ relative to
is an explanation of φ relative to ![[image]](images/eqn1299.jpg) , then for all probability distributions Pr on
, then for all probability distributions Pr on ![[image]](images/eqn1300.jpg) ,
, ![[image]](images/eqn1301.jpg) is a partial explanation of φ relative to (
is a partial explanation of φ relative to (![[image]](images/eqn1302.jpg) , Pr) with goodness (1, 1).
, Pr) with goodness (1, 1).
In Example 7.2.1, if the agent believes that it is sunny in the Canary Islands with probability.9, independent of whether Victoria actually goes to the Canaries or the tanning salon, then Victoria going to the Canaries is a partial explanation of her being tanned with goodness (α, β), where α ≥.9 and β ≥.9 (according to the updated and modified HP definition; recall that the original HP definition gives arguably inappropriate causality ascriptions in this example). To see that α ≥.9, note the probability of Victoria going to the Canaries being a cause of her being tanned is already.9 conditional on her going to Canaries; it is at least as high conditional on her going to the Canaries and being tanned. Similarly, β ≥.9, since the set of contexts that satisfy SC3 consists of all contexts where it is sunny in the Canary Islands together with contexts where Victoria goes to the tanning salon and it is not sunny in the Canaries. Similarly, in Example 7.2.2, if the agent believes that the probability of the other mysterious causes being operative is.1 conditional on the picture tube being faulty (i.e., ![[image]](images/eqn1303.jpg) , then T = 0 is a partial explanation of P = 0 with goodness (.9, 1).
, then T = 0 is a partial explanation of P = 0 with goodness (.9, 1).
In the literature, there have been many attempts to define probabilistic notions of explanation, in the spirit of the probabilistic definition of causality discussed in Section 2.5. These definitions typically say that the explanation raises the probability of the explanandum. Just is the case of causality, rather than dealing with probabilistic explanations, we can use notions like partial causality, in the spirit of the following example.
Example 7.2.4 Suppose a Geiger counter is placed near a rock and the Geiger counter clicks. What’s an explanation? Assume that the agent does not know that the rock has uranium, and thus is somewhat radioactive, but considers it possible, and understands that being near a radioactive object causes a Geiger counter to click with some probability less than 1. Clearly being near the radioactive object raises the probability of the Geiger counter clicking, so it becomes an explanation according to the probabilistic accounts of explanation. If the Geiger counter necessarily clicks whenever it is placed near a radioactive object, then Definition 7.1.1 would declare being near a radioactive object the explanation without difficulty. But since the clicking happens only with some probability β < 1, there must be some context that the agent considers possible where the Geiger counter would not click, despite being placed near the rock. Thus, the second half of EX1 does not hold, so being put close to the rock is not an explanation of the Geiger counter clicking according to Definition 7.1.1. However, it is a partial explanation, with goodness (1, β): moving the Geiger counter close to the rock is an explanation of it ticking relative to the set of contexts where it actually does tick, and the probability of such a context, by assumption, is β. ■
My sense is that most explanations are partial, although if α and β are close to 1, we call them “explanations” rather than “partial explanations”. The partiality may help explain why explanations attenuate over longer chains: even though, for each link, the parameters α and β may be close to 1, over the whole chain, α and β can get close to 0. For example, while Sylvia’s depression might be viewed as a reasonably good explanation of her depression, and Sylvia’s genetic makeup might be viewed as a reasonably good explanation of her depression, Sylvia’s genetic makeup might not be viewed as a particularly good explanation of her suicide.
Although the parameters α and β in the notion of partial explanation do give a good sense of the quality of an explanation, they do not tell the whole story, even if our notion of “goodness” is concerned only with likelihood. For one thing, as I mentioned earlier, we are interested in the probability of the explanation or, even better, the probability of the explanation conditional on the explanandum (i.e., ![[image]](images/eqn1304.jpg) ). But there may be a tension between these measures. For example, suppose that, in the disjunctive forest-fire model, we add another context u4 where there is no lightning, the arsonist drops a match, but there is no forest fire (suppose that, in u4, someone is able to stamp out the forest fire before it gets going). For definiteness, suppose that Pr(u1) =.1, Pr(u2) =.8, and Pr(u4) =.1, so the probability of having only lightning is.1, the probability of the arsonist dropping the match and starting the forest fire is.8, and the probability of the arsonist dropping a match and there being no fire is.1. In this case, the lightning is an explanation of the fire, and thus is a partial explanation with goodness (1, 1), but it has probability only 1/9 conditional on there being a fire. Although the arsonist is not an explanation of the fire, his dropping a match is a partial explanation of the fire with goodness (1,.9), and the arsonist has probability 8/9 conditional on there being a fire.
). But there may be a tension between these measures. For example, suppose that, in the disjunctive forest-fire model, we add another context u4 where there is no lightning, the arsonist drops a match, but there is no forest fire (suppose that, in u4, someone is able to stamp out the forest fire before it gets going). For definiteness, suppose that Pr(u1) =.1, Pr(u2) =.8, and Pr(u4) =.1, so the probability of having only lightning is.1, the probability of the arsonist dropping the match and starting the forest fire is.8, and the probability of the arsonist dropping a match and there being no fire is.1. In this case, the lightning is an explanation of the fire, and thus is a partial explanation with goodness (1, 1), but it has probability only 1/9 conditional on there being a fire. Although the arsonist is not an explanation of the fire, his dropping a match is a partial explanation of the fire with goodness (1,.9), and the arsonist has probability 8/9 conditional on there being a fire.
As if that wasn’t enough, there is yet another measure of goodness that people are quite sensitive to. Suppose that we are scientists wondering why there is a fire in the chemistry lab. We suspect an arsonist. But suppose that we include in the model an endogenous variable O representing the presence of oxygen. Ignoring normality considerations, O = 1 is certainly a cause of the fire in all contexts, and it holds with probability 1. It is a trivial explanation (i.e., it does not satisfy EX4), so that perhaps might be a reason to exclude it. But now suppose that we add an extremely unlikely context where O = 0 and yet there is a fire (perhaps it is possible to evacuate the oxygen from the lab, yet still create a fire using some other oxidizing substance). In that case, O = 1 is still an explanation of the fire, and it has high probability conditional on there being a fire. Nevertheless, it is an explanation with, intuitively, very little explanatory power. We would typically prefer the explanation that an arsonist started the fire, even though this might not have such high probability. How can we make this precise?
Here it is useful that we started with a set ![[image]](images/eqn1305.jpg) of contexts that can be viewed as the contexts that the agent considers possible before making the observation (in this case, before observing the fire), and that we view Pr as intuitively representing the agent’s “pre-observation” prior probability. Roughly speaking, I would like to define the explanatory power of a (partial) explanation
of contexts that can be viewed as the contexts that the agent considers possible before making the observation (in this case, before observing the fire), and that we view Pr as intuitively representing the agent’s “pre-observation” prior probability. Roughly speaking, I would like to define the explanatory power of a (partial) explanation ![[image]](images/eqn1306.jpg) as
as ![[image]](images/eqn1307.jpg) . This describes how likely φ becomes on learning
. This describes how likely φ becomes on learning ![[image]](images/eqn1308.jpg) . Taking LF to stand for lab fire, if lab fires are not common, Pr(⟦LF = 1⟧ ⟦O = 1⟧) is essentially equal to Pr(⟦LF = 1⟧) and is not so high. Thus, oxygen has low explanatory power for the fire in the lab. In contrast, Pr(⟦LF = 1⟧ ⟦MD = 1⟧) is likely to be quite high; learning that there is an arsonist who dropped a match makes the lab fire much more likely.
. Taking LF to stand for lab fire, if lab fires are not common, Pr(⟦LF = 1⟧ ⟦O = 1⟧) is essentially equal to Pr(⟦LF = 1⟧) and is not so high. Thus, oxygen has low explanatory power for the fire in the lab. In contrast, Pr(⟦LF = 1⟧ ⟦MD = 1⟧) is likely to be quite high; learning that there is an arsonist who dropped a match makes the lab fire much more likely.
Although this definition captures some important intuitions, it is not quite what we want. The problem is that it confounds correlation with causation. For example, according to this definition, the barometer falling would have high explanatory power for rain (although it is not a cause of rain). The following definition replaces the ![[image]](images/eqn1309.jpg) by
by ![[image]](images/eqn1310.jpg) , the set of contexts where a conjunct of
, the set of contexts where a conjunct of ![[image]](images/eqn1311.jpg) is part of a cause of φ.
is part of a cause of φ.
Definition 7.2.5 The explanatory power of the partial explanation ![[image]](images/eqn1312.jpg) for φ relative to (
for φ relative to (![[image]](images/eqn1313.jpg) , Pr) is
, Pr) is ![[image]](images/eqn1314.jpg) . ■
. ■
If ![[image]](images/eqn1315.jpg) is an explanation of φ (rather than just being a partial explanation of φ), then
is an explanation of φ (rather than just being a partial explanation of φ), then ![[image]](images/eqn1316.jpg) , and Definition 7.2.5 agrees with the original informal definition. The difference between the two definitions arises if there are contexts where φ and
, and Definition 7.2.5 agrees with the original informal definition. The difference between the two definitions arises if there are contexts where φ and ![[image]](images/eqn1317.jpg) both happen to be true, but
both happen to be true, but ![[image]](images/eqn1318.jpg) is not a cause of φ. In Example 7.2.1, the context where Victoria went to the Canary Islands, it was not sunny, but Victoria also went to the tanning salon, and so got tanned is one such example. Because of this difference, according to Definition 7.2.5, a falling barometer has 0 explanatory power for explaining the rain. Even though the barometer falls in almost all contexts where it rains (there may be some contexts where the barometer is defective, so it does not fall even if it rains), the barometer falling is not a cause of the rain in any context. Making the barometer rise would not result in the rain stopping!
is not a cause of φ. In Example 7.2.1, the context where Victoria went to the Canary Islands, it was not sunny, but Victoria also went to the tanning salon, and so got tanned is one such example. Because of this difference, according to Definition 7.2.5, a falling barometer has 0 explanatory power for explaining the rain. Even though the barometer falls in almost all contexts where it rains (there may be some contexts where the barometer is defective, so it does not fall even if it rains), the barometer falling is not a cause of the rain in any context. Making the barometer rise would not result in the rain stopping!
There is a tension between the explanatory power, the goodness, and the probability of a partial explanation. As we have seen, O = 1 has low explanatory power for LF = 1, although it has high probability conditional on the fire and has goodness (1, 1) (or close to it, if there is a context where there is a fire despite the lack of oxygen). For another example, in Example 7.1.4, as we observed, ES J = 1 is not an explanation of the forest fire in June (FF J = 1) relative to ![[image]](images/eqn1319.jpg) . The problem is the context (0, 1, 1), which does not satisfy [ESJ ←1](FF J = 1), so the second half of EX1 (i.e., SC3) does not hold. If Pr((0, 1, 1)) = p and Pr(⟦ESJ = 1⟧) = q, then the explanatory power of ES J = 1 is
. The problem is the context (0, 1, 1), which does not satisfy [ESJ ←1](FF J = 1), so the second half of EX1 (i.e., SC3) does not hold. If Pr((0, 1, 1)) = p and Pr(⟦ESJ = 1⟧) = q, then the explanatory power of ES J = 1 is ![[image]](images/eqn1320.jpg) , the probability of ES J = 1 conditional on there being a fire in June is 1, and ES J = 1 is a partial explanation of the fire in June with goodness (1, 1 – p). By way of contrast, AS = 1 ∧ ES J = 1 has goodness (1, 1) and explanatory power 1, but may have much lower probability than ES J = 1 conditional on there being a fire in June.
, the probability of ES J = 1 conditional on there being a fire in June is 1, and ES J = 1 is a partial explanation of the fire in June with goodness (1, 1 – p). By way of contrast, AS = 1 ∧ ES J = 1 has goodness (1, 1) and explanatory power 1, but may have much lower probability than ES J = 1 conditional on there being a fire in June.
There is no obvious way to resolve the tension between these various measures of the goodness of an explanation. A modeler must just decide what is most important. Things get even worse if we allow disjunctive explanations. The probability of a disjunctive explanation will be higher than that of its disjuncts, so according to that metric, disjunctive explanations are better. What about the goodness of a disjunctive partial explanation? It is not quite clear how to define this. Perhaps the most natural way of defining goodness would be to take its goodness to be the maximum goodness of each of its disjuncts, but if there are two disjuncts, one of which has goodness (.8,.9), while the other has goodness (.9,.8), which one has maximum goodness?
There is an intuition that a disjunctive explanation has less explanatory power than its disjuncts. This intuition can be captured in a natural way by taking the explanatory power of the disjunction ![[image]](images/eqn1321.jpg) for φ relative to (
for φ relative to (![[image]](images/eqn1322.jpg) , Pr) to be
, Pr) to be
![[image]](images/eqn1323.jpg) (7.1)
(7.1)
Thus, rather than taking the explanatory power of the disjunction ![[image]](images/eqn1324.jpg) to be
to be ![[image]](images/eqn1325.jpg) , which would be the obvious generalization of Definition 7.2.5, what (7.1) says is that, for each disjunct
, which would be the obvious generalization of Definition 7.2.5, what (7.1) says is that, for each disjunct ![[image]](images/eqn1326.jpg) , we consider how likely it is that
, we consider how likely it is that ![[image]](images/eqn1327.jpg) is a cause of φ conditional on learning the disjunction, and identify the explanatory power of the disjunction with the maximum likelihood, taken over all disjuncts.
is a cause of φ conditional on learning the disjunction, and identify the explanatory power of the disjunction with the maximum likelihood, taken over all disjuncts.
The notion of explanatory power helps explain why we are less interested in trivial explanations, even though they have high probability conditional on the explanandum (probability 1, in fact). They typically have worse explanatory power than nontrivial explanations.
These notions of goodness could be refined further by bringing normality into the picture. However, I have not yet explored how to best do this.
7.3 The General Definition of Explanation
In general, an agent may be uncertain about the causal model, so an explanation will have to include information about it. It is relatively straightforward to extend Definition 7.1.1 to accommodate this provision. Now an epistemic state ![[image]](images/eqn1328.jpg) consists not only of contexts, but of causal settings, that is, pairs (M,
consists not only of contexts, but of causal settings, that is, pairs (M, ![[image]](images/eqn1329.jpg) ) consisting of a causal model M and a context
) consisting of a causal model M and a context ![[image]](images/eqn1330.jpg) . Intuitively, now an explanation should consist of some causal information (such as “prayers do not cause fires”) and some facts that are true.
. Intuitively, now an explanation should consist of some causal information (such as “prayers do not cause fires”) and some facts that are true.
I assume that the causal information in an explanation is described by a formula ψ in the causal language. For example, ψ could say things like “prayers do not cause fires”, which corresponds to the formula (F = 0) ⇒ [P ← 1](F = 1), where P is a variable describing whether prayer takes place and F = 0 says that there is no fire; that is, if there is no fire, then praying won’t result in a fire. I take a (general) explanation to have the form (ψ, ![[image]](images/eqn1331.jpg) ), where ψ is an arbitrary formula in the causal language and, as before,
), where ψ is an arbitrary formula in the causal language and, as before, ![[image]](images/eqn1332.jpg) is a conjunction of primitive events. The first component in a general explanation restricts the set of causal models. Recall from Section 5.4 that ψ is valid in causal model M, written M ⊨ ψ, if
is a conjunction of primitive events. The first component in a general explanation restricts the set of causal models. Recall from Section 5.4 that ψ is valid in causal model M, written M ⊨ ψ, if ![[image]](images/eqn1333.jpg) for all contexts
for all contexts ![[image]](images/eqn1334.jpg) .
.
I now extend the Definition 7.1.1 to the more general setting where ![[image]](images/eqn1335.jpg) consists of arbitrary causal settings, dropping the assumption that the causal model is known. Conditions EX3 and EX4 remain unchanged; the differences arise only in EX1 and EX2. Let
consists of arbitrary causal settings, dropping the assumption that the causal model is known. Conditions EX3 and EX4 remain unchanged; the differences arise only in EX1 and EX2. Let ![[image]](images/eqn1336.jpg) .
.
Definition 7.3.1 (ψ, ![[image]](images/eqn1337.jpg) =
= ![[image]](images/eqn1338.jpg) ) is an explanation of φ relative to a set
) is an explanation of φ relative to a set ![[image]](images/eqn1339.jpg) of causal settings if the following conditions hold:
of causal settings if the following conditions hold:
EX1. ![[image]](images/eqn1340.jpg) is a sufficient cause of φ in all causal settings
is a sufficient cause of φ in all causal settings ![[image]](images/eqn1341.jpg) satisfying
satisfying ![[image]](images/eqn1342.jpg) such that M ⊨ ψ. More precisely,
such that M ⊨ ψ. More precisely,
![[image]](images/eqn1343.jpg) , then there exists a conjunct X = x of
, then there exists a conjunct X = x of ![[image]](images/eqn1344.jpg) and a (possibly empty) conjunction
and a (possibly empty) conjunction ![[image]](images/eqn1345.jpg) such that
such that ![[image]](images/eqn1346.jpg) is a cause of φ in (M,
is a cause of φ in (M, ![[image]](images/eqn1347.jpg) ).
).![[image]](images/eqn1348.jpg) for all causal settings
for all causal settings ![[image]](images/eqn1349.jpg) such that M ⊨ ψ.
such that M ⊨ ψ.EX2. ![[image]](images/eqn1350.jpg) is minimal; there is no pair
is minimal; there is no pair ![[image]](images/eqn1351.jpg) satisfying EX1 such that either
satisfying EX1 such that either ![[image]](images/eqn1352.jpg) (where “⊃” denotes strict superset),
(where “⊃” denotes strict superset), ![[image]](images/eqn1353.jpg) , and
, and ![[image]](images/eqn1354.jpg) is the restriction of
is the restriction of ![[image]](images/eqn1355.jpg) to
to ![[image]](images/eqn1356.jpg) , or
, or ![[image]](images/eqn1357.jpg) , and
, and ![[image]](images/eqn1358.jpg) is the restriction of
is the restriction of ![[image]](images/eqn1359.jpg) to
to ![[image]](images/eqn1360.jpg) . Roughly speaking, this says that no subset of
. Roughly speaking, this says that no subset of ![[image]](images/eqn1361.jpg) provides a sufficient cause of φ in more contexts than
provides a sufficient cause of φ in more contexts than ![[image]](images/eqn1362.jpg) does, and no strict subset of
does, and no strict subset of ![[image]](images/eqn1363.jpg) provides a sufficient cause of φ in the same set of contexts as
provides a sufficient cause of φ in the same set of contexts as ![[image]](images/eqn1364.jpg) does.
does.
EX3. ![[image]](images/eqn1365.jpg) .
.
The explanation is nontrivial if it satisfies in addition
EX4. ![[image]](images/eqn1366.jpg) for some
for some ![[image]](images/eqn1367.jpg) for some
for some ![[image]](images/eqn1368.jpg) . ■
. ■
Note that in EX1, the sufficient causality requirement is restricted to causal settings ![[image]](images/eqn1369.jpg) such that both M ⊨ ψ and
such that both M ⊨ ψ and ![[image]](images/eqn1370.jpg) . Although both components of an explanation are formulas in the causal language, they play different roles. The first component serves to restrict the set of causal models considered to those with the appropriate structure; the second describes a cause of φ in the resulting set of situations.
. Although both components of an explanation are formulas in the causal language, they play different roles. The first component serves to restrict the set of causal models considered to those with the appropriate structure; the second describes a cause of φ in the resulting set of situations.
Clearly Definition 7.1.1 is the special case of Definition 7.3.1 where there is no uncertainty about the causal structure (i.e., there is some M such that if ![[image]](images/eqn1371.jpg) , then M = M′). In this case, it is clear that we can take ψ in the explanation to be true.
, then M = M′). In this case, it is clear that we can take ψ in the explanation to be true.
Example 7.3.2 Paresis develops only in patients who have been syphilitic for a long time, but only a small number of patients who are syphilitic in fact develop paresis. For simplicity, suppose that no other factor is known to be relevant in the development of paresis. This description is captured by a simple causal model MP. There are two endogenous variables, S (for syphilis) and P (for paresis), and two exogenous variables, U1, the background factors that determine S, and U2, which intuitively represents “disposition to paresis”, that is, the factors that determine, in conjunction with syphilis, whether paresis actually develops. An agent who knows this causal model and that a patient has paresis does not need an explanation of why: he knows without being told that the patient must have syphilis and that U2 = 1. In contrast, for an agent who does not know the causal model (i.e., considers a number of causal models of paresis possible), (ψP, S = 1) is an explanation of paresis, where ψP is a formula that characterizes MP. ■
Although issues concerning scientific explanation have been discussed by philosophers for millennia, the mainstays of recent discussion have been Hempel’s [1965] deductive-nomological model and Salmon’s [1970] statistical relevance model. Woodward [2014] provides a good recent overview of work in philosophy on explanation. Although many have noted the connection between explanation and causation, there are not too many formal definitions of explanation in terms of causality in the literature. In particular, the definitions given by Hempel and Salmon do not really involve causality. In later work, Salmon [1984] did try to bring causality into his definitions, using the so-called process theories of causation [Dowe 2000], although he tried to do so without using counterfactuals. Gärdenfors [1980, 1988] and Van Fraassen [1980], among others, give definitions of probabilistic explanation that involves the explanation raising the probability of the explanandum. As I said in the main text, Salmon [1984] introduced the notions of ontic and epistemic explanation.
Lewis [1986a] does relate causality and explanation; he defends the thesis that “to explain an event is to provide some information about its causal history”. Although this view is compatible with the definition given here, there is no formal definition given to allow for a careful comparison between the approaches. Woodward [2003] clearly views explanation as causal explanation and uses a theory of causality based on structural equations. But he does not provide different definitions of causality and explanation, and he does not have a notion of explanation that depends on epistemic state. As a consequence, he has no analogues to the various notions of goodness of explanation considered here.
The definition of explanation given here, as well as much of the material in this chapter, is based on material in [Halpern and Pearl 2005b]. However, there are some significant differences between the definition given here and that in [Halpern and Pearl 2005b]; perhaps the most significant is the requirement of sufficient causality here (essentially, SC3). As I argued in Section 7.1, requiring sufficient causality seems to give a notion of explanation that corresponds more closely to natural language usage.
The idea that an explanation should be relative to an agent’s epistemic state is discussed at length by Gärdenfors [1988]. The idea appears in Gärdenfors’ earlier work [Gärdenfors 1980] as well; it is also explicit in Salmon’s [1984] notion of epistemic explanation. The observation that explanations may include (fragments of) a causal model is due to Gärdenfors [1980, 1988], as is the example of Mr. Johanssen. Hempel [1965] also observed that an explanation will have to be relative to uncertainty involving not just the context but also the causal model. However, neither Gärdenfors nor Hempel explicitly incorporated causality into their definitions, focusing instead on statistical and nomological information (i.e., information about basic physical laws).
Example 7.1.4 is due to Bennett (see [Sosa and Tooley 1993, pp. 222–223]). The analysis follows along the lines of the analysis in [Halpern and Pearl 2005b]. Example 7.2.1 is due to Gärdenfors [1988]. He pointed out that we normally accept “Victoria took a vacation in the Canary Islands” as a satisfactory explanation of Victoria being tanned; indeed, according to his definition, it is an explanation.
The notion of partial explanation defined here is related to, but different from, that of Chajewska and Halpern [1997]. Gärdenfors identifies the explanatory power of the (partial) explanation ![[image]](images/eqn1372.jpg) of φ with
of φ with ![[image]](images/eqn1373.jpg) (see [Chajewska and Halpern 1997; Gärdenfors 1988]). More precisely, Gärdenfors take the explanatory power of
(see [Chajewska and Halpern 1997; Gärdenfors 1988]). More precisely, Gärdenfors take the explanatory power of ![[image]](images/eqn1374.jpg) to be
to be ![[image]](images/eqn1375.jpg) . As far as comparing the explanatory power of two explanations for φ, it suffices to consider just
. As far as comparing the explanatory power of two explanations for φ, it suffices to consider just ![[image]](images/eqn1376.jpg) , since the Pr(⟦φ⟧) term appears in both expressions. Chajewska and Halpern [1997] argued that the quotient
, since the Pr(⟦φ⟧) term appears in both expressions. Chajewska and Halpern [1997] argued that the quotient ![[image]](images/eqn1377.jpg) gives a better measure of explanatory power than the difference, but the issues raised by Chajewska and Halpern are somewhat orthogonal to the concerns of this chapter.
gives a better measure of explanatory power than the difference, but the issues raised by Chajewska and Halpern are somewhat orthogonal to the concerns of this chapter.
The dominant approach to explanation in the Artificial Intelligence literature is the maximum a posteriori (MAP) approach; see, for example, [Henrion and Druzdzel 1990; Pearl 1988; Shimony 1991] for a discussion. The MAP approach focuses on the probability of the explanation, that is, ![[image]](images/eqn1378.jpg) . It is based on the intuition that the best explanation for an observation is the state of the world (in the language of this book, the context) that is most probable given the evidence. Although this intuition is quite reasonable, it completely ignores the issue of explanatory power, an issue that people are quite sensitive to. The formula O = 1 has high probability in the lab fire example, even though most people would not consider the presence of oxygen a satisfactory explanation of the fire. To remedy this problem, more intricate combinations of the quantities
. It is based on the intuition that the best explanation for an observation is the state of the world (in the language of this book, the context) that is most probable given the evidence. Although this intuition is quite reasonable, it completely ignores the issue of explanatory power, an issue that people are quite sensitive to. The formula O = 1 has high probability in the lab fire example, even though most people would not consider the presence of oxygen a satisfactory explanation of the fire. To remedy this problem, more intricate combinations of the quantities ![[image]](images/eqn1379.jpg) , and Pr(⟦φ⟧) have been suggested to quantify the causal relevance of
, and Pr(⟦φ⟧) have been suggested to quantify the causal relevance of ![[image]](images/eqn1380.jpg) to φ, but, as Pearl [2000, p. 221] argues, without taking causality into account, it seems that we cannot capture explanation in a reasonable way.
to φ, but, as Pearl [2000, p. 221] argues, without taking causality into account, it seems that we cannot capture explanation in a reasonable way.
Fitelson and Hitchcock [2011] discuss a number of probabilistic measures of causal strength and the connections between them. Almost all of these can be translated to probabilistic measures of “goodness” of an explanation as well. The notions of partial explanation and explanatory power that I have discussed here certainly do not exhaust the possibilities. Schupbach [2011] also considers various approaches to characterizing explanatory power in probabilistic terms.
Example 7.3.2 is due to Scriven [1959]. Apparently there are now other known factors, but this does not change the import of the example.
Applying the Definitions
Throughout history, people have studied pure science from a desire to understand the universe rather than practical applications for commercial gain. But their discoveries later turned out to have great practical benefits.
Stephen Hawking
In Chapter 1, I said that my goal was to get definitions of notions like causality, responsibility, and blame that matched our natural language usage of these words and were also useful. Now that we are rapidly approaching the end of the book, it seems reasonable to ask where we stand in this project.
First some good news: I hope that I have convinced most of you that the basic approach of using structural equations and defining causality in terms of counterfactuals can deal with many examples, especially once we bring normality into the picture. Moreover, the framework also allows us to define natural notions of responsibility, blame, and explanation. These notions do seem to capture many of the intuitions that people have in a natural way.
Next, some not-so-good news: One thing that has become clear to me in the course of writing this book is that things haven’t stabilized as much as I had hoped they would. Just in the process of writing the book, I developed a new definition of causality (the modified HP definition) and a new approach to dealing with normality (discussed in Section 3.5), and modified the definitions of responsibility, blame, and explanation (see the notes at the end of Chapters 6 and 7). Although I think that the latest definitions hold up quite well, particularly the modified HP definition combined with the alternative notion of normality, given that the modified HP definition is my third attempt at defining causality, and that other researchers continue to introduce new definitions, I certainly cannot be too confident that this is really the last word. Indeed, as I have indicated at various points in the book, there are some subtleties that the current definition does not seem to be capturing quite so well. To my mind, what is most needed is a good definition of agent-relative normality, which takes into account the issues discussed in Example 6.3.4 (where A and B can flip switches to determine whether C is shocked) and meshes well with the definition of causality, but doubtless others will have different concerns.
Moreover, when we try to verify experimentally the extent to which the definitions that we give actually measure how people ascribe causality and responsibility, the data become messy. Although the considerations discussed in Chapter 6 (pivotality, normality, and blame assignments) seem to do quite a good job of predicting how people will ascribe causal responsibility at a qualitative level, because all these factors (and perhaps others) affect people’s causality and responsibility judgments, it seems that it will be hard to design a clean theory that completely characterizes exactly how people acribe causality, responsibility, and blame at a more quantitative level.
So where does this leave us? I do not believe that there is one “true” definition of causality. We use the word in many different, but related, ways. It is unreasonable to expect one definition to capture them all. Moreover, there are a number of closely related notions—causality, blame, responsibility, intention—that clearly are often confounded. Although we can try to disentangle them at a theoretical level, people clearly do not always do so.
That said, I believe that it is important and useful to have precise formal definitions. To take an obvious example, legal judgments depend on causal judgments. A jury will award a large settlement to a patient if it believes that the patient’s doctor was responsible for an inappropriate outcome. Although we might disagree on whether and the extent to which the doctor was responsible, the disagreement should be due to the relevant facts in the case, not a disagreement about what causality and responsibility mean. Even if people confound notions like causality and responsibility, it is useful to get definitions that distinguish them (and perhaps other notions as well), so we can be clear about what we are discussing.
Although the definition(s) may not be able to handle all the subtleties, that is not necessary for them to be useful. I have discussed a number of different approaches here, and the jury is still out on which is best. The fact that the approaches all give the same answers in quite a few cases makes me even more optimistic about the general project.
I conclude the book with a brief discussion of three applications of causality related to computer science. These have the advantage that we have a relatively clear idea of what counts as a “good” definition. The modeling problem is also somewhat simpler; it is relatively clear exactly what the exogenous and endogenous variables should be, and what their ranges are, so some of the modeling issues encountered in Chapter 4 no longer arise.
The dominant approach to dealing with information security has been preventative: we try to prevent someone from accessing confidential data or connecting to a private network. More recently, there has been a focus on accountability: when a problem occurs, it should be possible after the fact to determine the cause of the problem (and then punish the perpetrators appropriately). Of course, dealing with accountability requires that we have good notions of causality and responsibility.
The typical assumption in the accountability setting, at least for computer science applications, is that we have logs that completely describe exactly what happened; there is no uncertainty about what happened. Moreover, in the background, there is a programming language. An adversary writes a program in some pre-specified programming language that interacts with the system. We typically understand the effect of changing various lines of code. The variables in the program can be taken to be the endogenous variables in the causal model. The programs used and the initial values of program variables are determined by the context. Changing some lines of code becomes an intervention. The semantics of the program in the language determines the causal model and the effect of interventions.
The HP definitions of causality and responsibility fit this application quite well. Of course, if some logs are missing, we can then move to a setting where there is an epistemic state, with a probability on contexts; the contexts of interest are the ones that would generate the portion of the log that is seen. If we are interested in a setting where there are several agents working together to produce some outcome, blame becomes even more relevant. Agents may have (possibly incorrect) beliefs about the programs that other agents are using. Issues of which epistemic state to use (the one that the agent actually had or the one that the agent should have had) become relevant. But the general framework of structural equations and the definitions provided here should work well.
A database is viewed as consisting of a large collection of tuples. A typical tuple may, for example, give an employee’s name, manager, gender, address, social security number, salary, and job title. A standard query in a database may have the form: tell me all employees who are programmer analysts, earn a salary of less than $100,000, and work for a manager earning a salary greater than $150,000. Causality in databases aims to answer the question: Given a query and a particular output of the query, which tuples in the database caused that output? This is of interest because we may be, for example, interested in explaining unexpected answers to a query. Tim Burton is a director well known for fantasy movies involving dark Gothic schemes, such as “Edward Scissorhands” and “Beetlejuice”. A user wishing to learn more about his work might query the IMDB movie database (www.imdb.com) about the genres of movies that someone named Burton directed. He might be surprised (and perhaps a little suspicious of the answer) when he learns that one genre is “Music and Musical”. He would then want to know which tuple (i.e., essentially, which movie) caused that output. He could then check whether there is an error in the database, or perhaps other directors named Burton who directed musicals. It turns out that Tim Burton did direct a musical (“Sweeney Todd”); there are also two other directors named Burton (David Burton and Humphrey Burton) who directed other musicals.
Another application of the causality definition is for diagnosing network failures. Consider a computer consisting of a number of servers, with physical links between them. Suppose that the database contains tuples of the form (Link (x, y), Active(x), Active(y)). Given a server x, Active(x) is either 0 or 1, depending on whether x is active; similarly Link (x, y) is either 0 or 1 depending on whether the link between x and y is up. Servers x and y are connected if there is a path of links between them, all of which are up, such that all servers on the path are active. Suppose that at some point the network administrator observes that servers x0 and y0 are no longer connected. This means that the query Connected (x0, y0) will return “false”. The causality query “Why did Connected (x0, y0) return ‘false’?” will return all the tuples (Link (x, y), Active(x), Active(y)) that are on some path from x0 to y0 such that either server x is not active, server y is not active, or the link between them is down. These are the potential causes of Connected (x0, y0) returning “false”.
I now briefly sketch how this is captured formally. As I said, a database D is taken to be a collection of tuples. For each tuple t, there is a binary variable Xt, which is 0 if the tuple t is not in the database of interest and 1 if it is. We are interested in causal models where the context determines the database. That is, the context determines which variables Xt are 1 and which are 0; there are no interesting structural equations. There is assumed to be a query language ![[image]](images/eqn1381.jpg) that is richer than the language
that is richer than the language ![[image]](images/eqn1382.jpg) introduced in Section 2.2.1. Each formula
introduced in Section 2.2.1. Each formula ![[image]](images/eqn1383.jpg) has a free variable x that ranges over tuples. There is a relation ⊨ such that, for each tuple t and formula
has a free variable x that ranges over tuples. There is a relation ⊨ such that, for each tuple t and formula ![[image]](images/eqn1384.jpg) , either D ⊨ φ(t) or D ⊨ ¬φ(t) (but not both). If D ⊨ φ(t), then t is said to satisfy the query φ in database D. In response to a query φ, a database D returns all the tuples t such that D ⊨ φ(t).
, either D ⊨ φ(t) or D ⊨ ¬φ(t) (but not both). If D ⊨ φ(t), then t is said to satisfy the query φ in database D. In response to a query φ, a database D returns all the tuples t such that D ⊨ φ(t).
We can easily build a causal language based on ![[image]](images/eqn1385.jpg) in the spirit of
in the spirit of ![[image]](images/eqn1386.jpg) . That is, instead of starting with Boolean combinations of formulas of the form X = x, we start with formulas of the form φ(t), where
. That is, instead of starting with Boolean combinations of formulas of the form X = x, we start with formulas of the form φ(t), where ![[image]](images/eqn1387.jpg) and t is a tuple in addition to formulas of the form Xt = i for i ∈ {0, 1}. If M is a causal model for databases, since each causal setting (M,
and t is a tuple in addition to formulas of the form Xt = i for i ∈ {0, 1}. If M is a causal model for databases, since each causal setting (M, ![[image]](images/eqn1388.jpg) ) determines a database, (M,
) determines a database, (M, ![[image]](images/eqn1389.jpg) ) ⊨ φ(t) exactly if D ⊨ φ(t), where D is the database determined by (M,
) ⊨ φ(t) exactly if D ⊨ φ(t), where D is the database determined by (M, ![[image]](images/eqn1390.jpg) ) and (M,
) and (M, ![[image]](images/eqn1391.jpg) ) ⊨ Xt = 1 exactly if t ∈ D. We can then define
) ⊨ Xt = 1 exactly if t ∈ D. We can then define ![[image]](images/eqn1392.jpg) just as in Section 2.2.1.
just as in Section 2.2.1.
Of course, for causality queries to be truly useful, it must be possible to compute them efficiently. To do this, a slight variant of the updated HP definition has been considered. Say that tuple t is a cause of the answer t′ for φ if
D1. (M, ![[image]](images/eqn1393.jpg) ) ⊨ (Xt = 1) ∧ φ(t′) (so t ∈ D and D ⊨ φ(t′), where D is the database determined by (M,
) ⊨ (Xt = 1) ∧ φ(t′) (so t ∈ D and D ⊨ φ(t′), where D is the database determined by (M, ![[image]](images/eqn1394.jpg) )); and
)); and
D2. there exists a (possibly empty) set T of tuples contained in D such that t ∉ T, D − T ⊨ φ(t′), and D − (T ∪ {t}) ⊨ ¬φ(t′).
If the tuple t is a cause of the answer t′ for φ in (M, ![[image]](images/eqn1395.jpg) ), then Xt = 1 is a cause of φ(t′) in (M,
), then Xt = 1 is a cause of φ(t′) in (M, ![[image]](images/eqn1396.jpg) ). D1 is just AC1. Translating to the kinds of formulas that we have been using all along, and taking
). D1 is just AC1. Translating to the kinds of formulas that we have been using all along, and taking ![[image]](images/eqn1397.jpg) to consist of all the variables Xt″ such that t″ ∈ T, the second clause says:
to consist of all the variables Xt″ such that t″ ∈ T, the second clause says: ![[image]](images/eqn1398.jpg) and
and ![[image]](images/eqn1399.jpg) . Thus, it is saying that
. Thus, it is saying that ![[image]](images/eqn1400.jpg) is a witness to the fact that Xt = 1 is a cause of φ(t′) according to the original HP definition; AC2(bo) holds. Note that AC3 is satisfied vacuously.
is a witness to the fact that Xt = 1 is a cause of φ(t′) according to the original HP definition; AC2(bo) holds. Note that AC3 is satisfied vacuously.
This does not necessarily make Xt = 0 a cause of φ(t′) according to the updated HP definition. There may be a subset T′ of T such that ![[image]](images/eqn1401.jpg) , in which case AC2(bu) would fail. Things are better if we restrict to monotone queries, that is, queries ψ such that for all t′, if D ⊨ ψ(t′) and D ⊆ D′, then D′ ⊨ ψ(t′) (in words, if ψ(t′) holds for a small database, then it is guaranteed to hold for larger databases, with more tuples). Monotone queries arise often in practice, so proving results for monotone queries is of practical interest. If φ is a monotone query, then AC2(bu) holds as well: if
, in which case AC2(bu) would fail. Things are better if we restrict to monotone queries, that is, queries ψ such that for all t′, if D ⊨ ψ(t′) and D ⊆ D′, then D′ ⊨ ψ(t′) (in words, if ψ(t′) holds for a small database, then it is guaranteed to hold for larger databases, with more tuples). Monotone queries arise often in practice, so proving results for monotone queries is of practical interest. If φ is a monotone query, then AC2(bu) holds as well: if ![[image]](images/eqn1402.jpg) , then for all subsets T′ of T, we must have
, then for all subsets T′ of T, we must have ![[image]](images/eqn1403.jpg) (because
(because ![[image]](images/eqn1404.jpg) , and if T′ ⊆ T, then D – T ⊆ D – T′, so we can appeal to monotonicity). It is also easy to see that for a monotone query, this definition also guarantees that Xt = 1 is part of a cause of φ(t′) according to the modified HP definition.
, and if T′ ⊆ T, then D – T ⊆ D – T′, so we can appeal to monotonicity). It is also easy to see that for a monotone query, this definition also guarantees that Xt = 1 is part of a cause of φ(t′) according to the modified HP definition.
The second clause has some of the flavor of responsibility; we are finding a set such that removing this set from D results in t being critical for φ(t′). Indeed, we can define a notion of responsibility in databases by saying that tuple t has degree of responsibility 1/(k + 1) for the answer t′ for φ if k is the size of the smallest set T for which the definition above holds.
Notice that I said “if t is a cause of the answer t′ for φ in (M, ![[image]](images/eqn1405.jpg) ), then Xt = 1 is a cause of φ(t′) in (M,
), then Xt = 1 is a cause of φ(t′) in (M, ![[image]](images/eqn1406.jpg) )”; I did not say “if and only if”. The converse is not necessarily true. The only witnesses (
)”; I did not say “if and only if”. The converse is not necessarily true. The only witnesses (![[image]](images/eqn1407.jpg) ,
,![[image]](images/eqn1408.jpg) , 0) that this definition allows are ones where
, 0) that this definition allows are ones where ![[image]](images/eqn1409.jpg) . That is, in determining whether the counterfactual clause holds, we can consider only witnesses that involve removing tuples from the database, not witnesses that might add tuples to the database. This can be captured in terms of a normality ordering that makes it abnormal to add tuples to the database but not to remove them. However, the motivation for this restriction is not normality as discussed in Chapter 3, but computational. For causality queries to be of interest, it must be possible to compute the answers quickly, even in huge databases, with millions of tuples. This restriction makes the computation problem much simpler. Indeed, it is known that for conjunctive queries (i.e., queries that can be written as conjunctions of basic queries about components of tuples in databases—I omit the formal definitions here), computing whether t is an actual cause of φ can be done in time polynomial in the size of the database, which makes it quite feasible. Importantly, conjunctive queries (which are guaranteed to be monotone) arise frequently in practice.
. That is, in determining whether the counterfactual clause holds, we can consider only witnesses that involve removing tuples from the database, not witnesses that might add tuples to the database. This can be captured in terms of a normality ordering that makes it abnormal to add tuples to the database but not to remove them. However, the motivation for this restriction is not normality as discussed in Chapter 3, but computational. For causality queries to be of interest, it must be possible to compute the answers quickly, even in huge databases, with millions of tuples. This restriction makes the computation problem much simpler. Indeed, it is known that for conjunctive queries (i.e., queries that can be written as conjunctions of basic queries about components of tuples in databases—I omit the formal definitions here), computing whether t is an actual cause of φ can be done in time polynomial in the size of the database, which makes it quite feasible. Importantly, conjunctive queries (which are guaranteed to be monotone) arise frequently in practice.
In model checking, the goal is to check whether a program satisfies a certain specification. When a model checker says that a program does not satisfy its specification, it typically provides in addition a counterexample that demonstrates the failure of the specification. Such a counterexample can be quite useful in helping the programmer understand what went wrong and in correcting the program. In many cases, however, understanding the counterexample can be quite challenging.
The problem is that counterexamples can be rather complicated objects. Specifications typically talk about program behavior over time, saying things like “eventually φ will happen”, “ψ will never happen’, and “property φ′ will hold at least until ψ′ does”. A counterexample is a path of the program; that is, roughly speaking, a possibly infinite sequence of tuples (x1,…, xn), where each tuple describes the values of the variables X1,…, Xn. Trying to understand from the path why the program did not satisfy its specification may not be so simple. As I now show, having a formal notion of causality can help in this regard.
Formally, we associate with each program a Kripke structure, a graph with nodes and directed edges. Each node is labeled with a possible state of the program. If X1,…, Xn are the variables in the program, then a program state just describes the values of these variables. For simplicity in this discussion, I assume that X1,…, Xn are all binary variables, although it is straightforward to extend the approach to non-binary variables (as long as they have finite range). The edges in the Kripke structure describe possible transitions of the program. That is, there is an edge from node v1 to node v2 if the program can make a transition from the program state labeling v1 to that labeling v2. The programs we are interested in are typically concurrent programs, which are best thought of as a collection of possibly communicating programs, each of which is run by a different agent in the system. (We can think of the order of moves as being determined exogenously.) This means that there may be several possible transitions from a given node. For example, at a node where X and Y both have value 0, one agent’s program may flip the value of X and another agent’s program may flip the value of Y. If these are the only variables, then there would be a transition from the node labeled (0, 0) to nodes labeled (1, 0) and (0, 1).
A path π = (s0, s1, s2, …) in M is a sequence of states such that each state sj is associated with a node in M and for all i, there is a directed edge from the node associated with si to the node associated with si+1. Although the use of the word “state” here is deliberately intended to suggest “program state”, technically they are different. Although two distinct states si and sj on a path might be associated with the same node (and thus the same program state), it is useful to think of them as being different so that we can talk about different occurrences of the same program state on a path. That said, I often blur the distinction between state and program state.
Kripke structures have frequently been used as models of modal logics, logics that extend propositional or first-order logic by including modal operators such as operators for belief or knowledge. For example, in a modal logic of knowledge, we can make statements like “Alice knows that Bob knows that p is true”. Temporal logic, which includes operators like “eventually”, “always”, and “until”, has been found to be a useful tool for specifying properties of programs. For example, the temporal logic formula □X says that X is always true (i.e., □X is true of a path π if X = 1 at every state in π). All the specifications mentioned above (“eventually φ will happen”, “ψ will never happen’, and “property φ′ will hold at least until ψ′ does”) can be described in temporal logic and evaluated on the paths of a Kripke structure. That is, there is a relation ⊨ such that, given a Kripke structure M, a path π, and a temporal logic formula φ, either (M, π) ⊨ φ or (M, π) ⊨ ¬φ, but not both. The details of temporal logic and the ⊨ relation are not necessary for the following discussion. All that we need is that (M, (s0, s1, s2, …)) ⊨ Dφ, where φ is a propositional formula, if φ is true at each state si.
A model checker may show that a program characterized by a Kripke structure M fails to satisfy a particular specification φ by returning (a compact description of) a possibly infinite path π in M that satisfies ¬φ. The path π provides a counterexample to M satisfying φ. As I said, although having such a counterexample is helpful, a programmer may want a deeper understanding of why the program failed to satisfy the specification. This is where causality comes in.
Beer, Ben-David, Chocker, Orni, and Trefler give a definition of causality in Kripke structures in the spirit of the HP definition. Specifically, they define what it means for the fact that X = x in the state si on a path π to be a cause of the temporal logic formula φ not holding in path π. (As an aside, rather than considering the value of the variable X in state s, for each state s and variable X in the program, we could have a variable Xs, and just ask whether Xs = x is a cause of φ. Conceptually, it seems more useful to think of the same variable as having different values in different states, rather than having many different variables Xs.) As with the notion of causality in databases, the language for describing what can be caused is richer than the language ![[image]](images/eqn1410.jpg) , but the basic intuitions behind the definition of causality are unchanged.
, but the basic intuitions behind the definition of causality are unchanged.
To formalize things, I need a few more definitions. Since we are dealing with binary variables, in a temporal logic formula, I write X rather than X = 1 and ¬X rather than X = 0. For example, I write X ∧ ¬Y rather than X = 1 ∧ Y = 0. Define the polarity of an occurrence of a variable X in a formula φ to be positive if X occurs in the scope of an even number of negations and negative if X occurs in the scope of an odd number of negations. Thus, for example, the first occurrence of X in a temporal formula such as ¬□(¬X ∧ Y) ∨ ¬X has positive polarity, the only occurrence of Y has negative polarity, and the second occurrence of X has negative polarity. (The temporal operators are ignored when computing the polarity of a variable.)
A pair (s, X) consisting of a state s and a variable X is potentially helpful for φ if either there exists at least one occurrence of X in φ that has positive polarity and X = 0 in s or there exists at least one occurrence of X in φ that has negative polarity and X = 1 in s. It is not hard to show that if (s, X) is not potentially helpful for φ, then changing the value of X in s cannot change the truth value of φ from false to true in π. (This claim is stated more formally below.)
Given distinct pairs (s1, X1),…, (sk, Xk) and a path π, let π[(s1, X1),…, (sk, Xk)] be the path that is just like π except that the value of Xi in state si is flipped, for i = 1,…, k. (We can think of π[(s1, X1),…, (sk, Xk)] as the result of intervening on π so as to flip the values of the variable Xi in state i, for i = 1,…, k.) Thus, the previous observation says that if (s, X) is not potentially helpful for φ and (M, π) ⊨ ¬φ, then (M, π[(s, X)]) ⊨ ¬φ.
Suppose that π is a counterexample to φ. A finite prefix ρ of π is said to be a counterexample to φ if (M, π′) ⊨ ¬φ for all paths π′ that extend ρ. Note that even if π is a counterexample to φ, there may not be any finite prefix of π that is a counterexample to φ. For example, if φ is the formula ¬□(X = 0), which says that X is not always 0, so eventually X = 1, a counterexample π is a path such that X = 0 at every state on the path. However, for every finite prefix ρ of π, there is an extension π′ of ρ that includes a state where X = 1, so ρ is not a counterexample.
A prefix ρ of π is said to be a minimal counterexample to φ if it is a counterexample to φ and there is no shorter prefix that is a counterexample to φ. If no finite prefix of π is a counterexample to φ, then π itself is a minimal counterexample to φ.
We are finally ready for the definition of causality.
Definition 8.3.1 If π is a counterexample to φ, then (s, X) (intuitively, the value of X in state s) is a cause of the first failure of φ on π if
Co1. there is a prefix ρ of π (which could be π itself) such that ρ is a minimal counterexample to φ and s is a state on ρ; and
Co2. there exist distinct pairs (s1, X1),…, (sk, Xk) potentially helpful for φ such that (M, ρ[(s1, X1),…, (sk, Xk)]) ⊨ ¬φ and (M, ρ[(s, X), (s1, X1),…, (sk, Xk)]) ⊨ φ. ■
Condition Co2 in Definition 8.3.1 is essentially a combination of AC2(a) and A2(bo), if we assume that the value of all variables is determined exogenously. Clearly the analogue of AC2(a) holds: changing the value of X in state s flips φ from true to false, under the contingency that the value of Xi is flipped in state si, for i = 1,…, k. Moreover, AC2(bo) holds, since leaving X at its value in state s while flipping X1,…, Xk keeps φ false.
To get an analogue of AC2(bu), we need a further requirement:
![[image]](images/eqn1411.jpg)
Finally, to get an analogue of AC2(am), we need yet another condition:
![[image]](images/eqn1412.jpg)
I use strict subset in Co4 since Co2 requires that (M, ρ[(s, X), (s1, X1),…, (sk, Xk)]) ⊨ φ. If Co2–4 hold, then the values of X, X1,…, Xk in state s together form a cause of φ according to the modified HP definition, and the value of X is part of a cause of φ.
Condition Co1 in Definition 8.3.1 has no analogue in the HP definition of actual causality (in part, because there is no notion of time in the basic HP framework). It was added here because knowing about the first failure of φ seems to be of particular interest to programmers. Also, focusing on one failure reduces the set of causes, which makes it easier for programmers to understand an explanation. Of course, the definition would make perfect sense without this clause.
Example 8.3.2 Suppose that (the program state labeling) node v satisfies X = 1 and node v′ satisfies X = 0. Assume that v and v′ are completely connected in the Kripke structure: there is an edge from v to itself, from v to v′, from v′ to itself, and from v′ to v. Consider the path π = (s0, s1, s2, …), where all states on the path are associated with v except s2, which is associated with v′. Clearly (M, π) ⊨ ¬□X. Indeed, if ρ = (s0, s1, s2), then □X already fails in ρ. Note that (s2, X) is potentially helpful for □X (since X has positive polarity in □X and X = 0 in s2). It is easy to check that (s2, X) is a cause of the first failure of □X in π.
Now consider the formula ¬□X. The path ![[image]](images/eqn1413.jpg) where each state
where each state ![[image]](images/eqn1414.jpg) is associated with v is a counterexample to ¬□X, but no finite prefix of π′ is a counterexample; it is always possible to extend a finite prefix so as to make ¬□X true (by making X = 0 at some state in the extension). The value of X in each of the states on π′ is a cause of ¬□X failing. ■
is associated with v is a counterexample to ¬□X, but no finite prefix of π′ is a counterexample; it is always possible to extend a finite prefix so as to make ¬□X true (by making X = 0 at some state in the extension). The value of X in each of the states on π′ is a cause of ¬□X failing. ■
Beer, Ben-David, Chocker, Orni, and Trefler built a tool that implemented these ideas; they report that programmers found it quite helpful.
Just as in the database case, the complexity of computing causality becomes significant in this application. In general, the complexity of computing causality in counterexamples is NP-complete. However, given a finite path ρ and a specification φ that fails in all paths extending ρ, there is an algorithm that runs in time polynomial in the length of ρ and φ (viewed as a string of symbols) that produces a superset of the causes of φ failing in ρ. Moreover, in many cases of practical interest, the set produced by the algorithm is precisely the set of causes. This algorithm is actually the one implemented in the tool.
Causality also turns out to be useful even if a program does satisfy its specification. In that case, a model checker typically provides no further information. The implicit assumption was that if the model checker says that a program satisfies its specification, then programmers are happy to leave well enough alone; they feel no need to further analyze the program. However, there has been growing awareness that further analysis may be necessary even if a model checker reports that a program satisfies its specification. The concern is that the reason that the program satisfies its specification is due to an error in the specification itself (the specification may not cover an important case). One way to minimize this concern is to try to understand what causes the program to satisfy its specification. And one useful way of formalizing this turns out to be to examine the degree of responsibility that the value of variable X in state s (i.e., a pair (s, X), in the notation of the earlier discussion) has for the program satisfying the specification. If there are states s such that (s, X) has a low degree of responsibility for a specification φ for all variables X, this suggests that s is redundant. Similarly, if there is a variable X such that (s, X) has a low degree of responsibility for φ for all states s, this suggests that X is redundant. In either case, we have a hint that there may be a problem with the specification: The programmer felt that state s (or variable X) was important, but it is not carrying its weight in terms of satisfying the specification. Understanding why this is the case may uncover a problem.
Again, while the general problem of computing degree of responsibility in this context is hard, there are tractable special cases of interest. It is necessary to identify these tractable cases and argue that they are relevant in practice for this approach to be considered worth-while.
These examples have a number of features that are worth stressing.
The applications in this chapter illustrate just how useful a good account of causality can be. Although the HP definition needed to be tweaked somewhat in these applications (both because of the richer languages involved and to decrease the complexity of determining causality), these examples, as well as the many other examples in the book, make me confident that the HP definition, augmented by a normality ordering if necessary, provides a powerful basis for a useful account of causality. Clearly more work can and should be done on refining and extending the definitions of causality, responsibility, and explanation. But I suspect that looking at the applications will suggest further research questions quite different from the traditional questions that researchers have focused on thus far. I fully expect that the coming years will give us further applications and a deeper understanding of the issues involved.
Lombrozo [2010] provides further evidence regarding the plethora of factors that affect causality ascriptions.
Feigenbaum, Jaggard, and Wright [2011] point out the role of causality in accountability ascriptions and suggest using the HP definition. Datta et al. [2015] explore the role of causality in accountability in greater detail. Although their approach to causality involves counterfactuals, there are some significant differences from the HP definition. Among other things, they use sufficient causality rather than what I have been calling “actual causality”.
Much of the material on the use of causality in databases is taken from the work of Meliou, Gatterbauer, Halpern, Koch, Moore, and Suciu [2010]. The complexity results for queries mentioned in the discussion (as well as other related results) are proved by Meliou, Gatterbauer, Moore, and Suciu [2010].
As I said in Section 8.3, Beer et. al. [2012] examined the use of causality in explaining counterexamples to the specification of programs. The causality computation was implemented in a counterexample explanation tool for the IBM hardware model checker RuleBase [Beer et al. 2012]. Programmers found the tool tremendously helpful. In fact, when it was temporarily disabled between releases, users called and complained about its absence [Chockler 2015].
Chockler, Halpern, and Kupferman [2008] considered the use of causality and responsibility to check whether specifications were appropriate, or if the programmer was trying to satisfy a specification different from the one that the model checker was checking. They provided a number of tractable cases of the problem.
Chockler, Grumberg, and Yadgar [2008] consider another application of responsibility (in the spirit of the HP definition) to model checking: refinement. Because programs can be so large and complicated, model checking can take a long time. One way to reduce the runtime is to start with a coarse representation of the program, where one event represents a family of events. Model checking a coarse representation is much faster than model checking a refined representation, but it may not produce a definitive answer. The representation is then refined until a definitive answer is obtained. Chockler, Grumberg, and Yadgar [2008] suggested that the way that the refinement process works could be guided by responsibility considerations. Roughly speaking, the idea is to refine events that are most likely to be responsible for the outcome. Again, they implemented their ideas in a model-checking tool and showed that it performed very well in practice.
Groce [2005] also used a notion of causality based on counterfactuals to explain errors in programs, although his approach was not based on the HP definitions.
Adams, E. (1975). The Logic of Conditionals. Dordrecht, Netherlands: Reidel.
Alechina, N., J. Y. Halpern, and B. Logan (2016). Causality, responsibility, and blame in team plans. Unpublished manuscript.
Aleksandrowicz, G., H. Chockler, J. Y. Halpern, and A. Ivrii (2014). The computational complexity of structure-based causality. In Proc. Twenty-Eighth National Conference on Artificial Intelligence (AAAI ’14), pp. 974–980. Full paper available at www.cs.cornell.edu/home/halpern/papers/newcause.pdf.
Alicke, M. (1992). Culpable causation. Journal of Personality and Social Psychology 63, 368–378.
Alicke, M. D., D. Rose, and D. Bloom (2011). Causation, norm violation, and culpable control. Journal of Philosophy 108, 670–696.
Alvarez, L. W., W. Alvarez, F. Asaro, and H. Michel (1980). Extraterrestrial cause for the Cretaceous–Tertiary extinction. Science 208(4448), 1095–1108.
Balke, A. and J. Pearl (1994). Probabilistic evaluation of counterfactual queries. In Proc. Twelfth National Conference on Artificial Intelligence (AAAI ’94), pp. 200–207.
Baumgartner, M. (2013). A regularity theoretic approach to actual causation. Erkenntnis 78(1), 85–109.
Beebee, H. (2004). Causing and nothingness. In J. Collins, N. Hall, and L. A. Paul (Eds.), Causation and Counterfactuals, pp. 291–308. Cambridge, MA: MIT Press.
Beer, I., S. Ben-David, H. Chockler, A. Orni, and R. J. Trefler (2012). Explaining counterexamples using causality. Formal Methods in System Design 40(1), 20–40.
Bell, J. S. (1964). On the Einstein Podolsky Rosen paradox. Physics 1(3), 195–200.
Bennett, J. (1987). Event causation: the counterfactual analysis. In Philosophical Perspectives, Vol. 1, Metaphysics, pp. 367–386. Atascadero, CA: Ridgeview Publishing Company.
Briggs, R. (2012). Interventionist counterfactuals. Philosophical Studies 160, 139–166.
Casati, R. and A. Varzi (2014). Events. In E. N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy (Fall 2014 edition). Available at http://plato.stanford.edu/archives/spr2014/entries/events/.
Chajewska, U. and J. Y. Halpern (1997). Defining explanation in probabilistic systems. In Proc. Thirteenth Conference on Uncertainty in Artificial Intelligence (UAI ’97), pp. 62–71.
Chockler, H. (2015). Personal email.
Chockler, H., O. Grumberg, and A. Yadgar (2008). Efficient automatic STE refinement using responsibility. In Proc. 14th Conference on Tools and Algorithms for the Construction and Analysis of Systems, pp. 233–248.
Chockler, H. and J. Y. Halpern (2004). Responsibility and blame: A structural-model approach. Journal of A.I. Research 20, 93–115.
Chockler, H., J. Y. Halpern, and O. Kupferman (2008). What causes a system to satisfy a specification? ACM Transactions on Computational Logic 9(3).
Chu, F. and J. Y. Halpern (2008). Great expectations. Part I: On the customizability of generalized expected utility. Theory and Decision 64(1), 1–36.
Cook, S. A. (1971). The complexity of theorem proving procedures. In Proc. 3rd ACM Symposium on Theory of Computing, pp. 151–158.
Cushman, F., J. Knobe, and W. Sinnott-Armstrong (2008). Moral appraisals affect doing/allowing judgments. Cognition 108(1), 281–289.
Datta, A., D. Garg, D. Kaynar, D. Sharma, and A. Sinha (2015). Program actions as actual causes: a building block for accountability. In Proc. 28th IEEE Computer Security Foundations Symposium.
Davidson, D. (1967). Causal relations. Journal of Philosophy LXIV(21), 691–703.
Dawid, A. P. (2007). Fundamenthals of statistical causality. Research Report No. 279, Dept. of Statistical Science, University College, London.
Dawid, A. P., D. L. Faigman, and S. E. Fienberg (2014). Fitting science into legal contexts: assessing effects of causes or causes of effects? Sociological Methods and Research 43(3), 359–390.
Dowe, P. (2000). Physical Causation. Cambridge, U.K.: Cambridge University Press.
Dubois, D. and H. Prade (1991). Possibilistic logic, preferential models, non-monotonicity and related issues. In Proc. Twelfth International Joint Conference on Artificial Intelligence (IJCAI ’91), pp. 419–424.
Eberhardt, F. (2014). Direct causes and the trouble with soft intervention. Erkenntnis 79(4), 755–777.
Eells, E. (1991). Probabilistic Causality. Cambridge, U.K.: Cambridge University Press.
Eells, E. and E. Sober (1983). Probabilistic causality and the question of transitivity. Philosophy of Science 50, 35–57.
Eiter, T. and T. Lukasiewicz (2002). Complexity results for structure-based causality. Artificial Intelligence 142(1), 53–89.
Fagin, R., J. Y. Halpern, Y. Moses, and M. Y. Vardi (1995). Reasoning About Knowledge. Cambridge, MA: MIT Press. A slightly revised paperback version was published in 2003.
Falcon, A. (2014). Aristotle on causality. In E. N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy (Spring 2014 edition). Available at http://plato.stanford.edu/archives/spr2014/entries/aristotle-causality.
Feigenbaum, J., A. D. Jaggard, and R. N. Wright (2011). Towards a formal model of accountability. In Proc. 14th New Security Paradigms Workshop (NSPW), pp. 45–56.
Fenton-Glynn, L. (2016). A proposed probabilistic extension of the Halpern and Pearl definition of actual cause. British Journal for the Philosophy of Science. To appear.
Fitelson, B. and C. Hitchcock (2011). Probabilistic measures of causal strength. In Causality in the Sciences, Chapter 29. Oxford, U.K.: Oxford University Press.
Frick, J. (2009). “Causal dependence” and chance: the new problem of false negatives. Unpublished manuscript.
Friedman, N. and J. Y. Halpern (1995). Plausibility measures: a user’s guide. In Proc. Eleventh Conference on Uncertainty in Artificial Intelligence (UAI ’95), pp. 175– 184.
Galles, D. and J. Pearl (1998). An axiomatic characterization of causal counterfactuals. Foundation of Science 3(1), 151–182.
Gärdenfors, P. (1980). A pragmatic approach to explanations. Philosophy of Science 47, 404–423.
Gärdenfors, P. (1988). Knowledge in Flux. Cambridge, MA: MIT Press.
Geffner, H. (1992). High probabilities, model preference and default arguments. Mind and Machines 2, 51–70.
Gerstenberg, T., N. D. Goodman, D. Lagnado, and J. B. Tenenbaum (2014). From couterfactual simulation to causal judgment. In Proc. 36th Annual Conference of the Cognitive Science Society (CogSci 2014), pp. 523–528.
Gerstenberg, T., N. D. Goodman, D. Lagnado, and J. B. Tenenbaum (2015). How, whether, why: causal judgments as counterfactual constraints. In Proc. 37th Annual Conference of the Cognitive Science Society (CogSci 2015).
Gerstenberg, T., J. Halpern, and J. B. Tenenbaum (2015). Responsiblity judgments in voting scenarios. In Proc. 37th Annual Conference of the Cognitive Science Society (CogSci 2015), pp. 788–793.
Gerstenberg, T. and D. Lagnado (2010). Spreading the blame: the allocation of responsibility amongst multiple agents. Cognition 115, 166–171.
Glymour, C., D. Danks, B. Glymour, F. Eberhardt, J. Ramsey, R. Scheines, P. Spirtes, C. M. Teng, and J. Zhang (2010). Actual causation: a stone soup essay. Synthese 175, 169–192.
Glymour, C. and F. Wimberly (2007). Actual causes and thought experiments. In J. Campbell, M. O’Rourke, and H. Silverstein (Eds.), Causation and Explanation, pp. 43–67. Cambridge, MA: MIT Press.
Goldberger, A. S. (1972). Structural equation methods in the social sciences. Econometrica 40(6), 979–1001.
Goldman, A. I. (1999). Why citizens should vote: a causal responsibility approach. Social Philosophy and Policy 16(2), 201–217.
Goldszmidt, M. and J. Pearl (1992). Rank-based systems: a simple approach to belief revision, belief update and reasoning about evidence and actions. In Principles of Knowledge Representation and Reasoning: Proc. Third International Conference (KR ’92), pp. 661–672.
Gomes, C. P., H. Kautz, A. Sabharwal, and B. Selman (2008). Satisfiability solvers. In Handbook of Knowledge Representation, pp. 89–133.
Good, I. J. (1961a). A causal calculus I. British Journal for the Philosophy of Science 11, 305–318.
Good, I. J. (1961b). A causal calculus II. British Journal for the Philosophy of Science 12, 43–51.
Groce, A. (2005). Error Explanation and Fault Localization with Distance Metrics. Ph. D. thesis, CMU.
Haavelmo, T. (1943). The statistical implications of a system of simultaneous equations. Econometrica 11, 1–12.
Hall, N. (2004). Two concepts of causation. In J. Collins, N. Hall, and L. A. Paul (Eds.), Causation and Counterfactuals. Cambridge, MA: MIT Press.
Hall, N. (2007). Structural equations and causation. Philosophical Studies 132, 109–136.
Halpern, J. Y. (1997). Defining relative likelihood in partially-ordered preferential structures. Journal of A.I. Research 7, 1–24.
Halpern, J. Y. (2000). Axiomatizing causal reasoning. Journal of A.I. Research 12, 317– 337.
Halpern, J. Y. (2001). Conditional plausibility measures and Bayesian networks. Journal of A.I. Research 14, 359–389.
Halpern, J. Y. (2003). Reasoning About Uncertainty. Cambridge, MA: MIT Press.
Halpern, J. Y. (2008). Defaults and normality in causal structures. In Principles of Knowledge Representation and Reasoning: Proc. Eleventh International Conference (KR ’08), pp. 198–208.
Halpern, J. Y. (2013). From causal models to possible-worlds models of counterfactuals. Review of Symbolic Logic 6(2), 305–322.
Halpern, J. Y. (2014a). Appropriate causal models and stability of causation. In Principles of Knowledge Representation and Reasoning: Proc. Fourteenth International Conference (KR ’14), pp. 198–207.
Halpern, J. Y. (2014b). The probability of causality. Unpublished manuscript.
Halpern, J. Y. (2015a). A modification of the Halpern-Pearl definition of causality. In Proc. 24th International Joint Conference on Artificial Intelligence (IJCAI 2015), pp. 3022–3033.
Halpern, J. Y. (2015b). Sufficient conditions for causality to be transitive. Philosophy of Science. To appear.
Halpern, J. Y. and C. Hitchcock (2010). Actual causation and the art of modeling. In R. Dechter, H. Geffner, and J. Halpern (Eds.), Causality, Probability, and Heuristics: A Tribute to Judea Pearl, pp. 383–406. London: College Publications.
Halpern, J. Y. and C. Hitchcock (2013). Compact representations of causal models. Cognitive Science 37, 986–1010.
Halpern, J. Y. and C. Hitchcock (2015). Graded causation and defaults. British Journal for the Philosophy of Science 66(2), 413–457.
Halpern, J. Y. and J. Pearl (2001). Causes and explanations: A structural-model approach. Part I: Causes. In Proc. Seventeenth Conference on Uncertainty in Artificial Intelligence (UAI 2001), pp. 194–202.
Halpern, J. Y. and J. Pearl (2005a). Causes and explanations: A structural-model approach. Part I: Causes. British Journal for Philosophy of Science 56(4), 843–887.
Halpern, J. Y. and J. Pearl (2005b). Causes and explanations: A structural-model approach. Part II: Explanations. British Journal for Philosophy of Science 56(4), 889–911.
Halpern, J. Y. and M. R. Tuttle (1993). Knowledge, probability, and adversaries. Journal of the ACM 40(4), 917–962.
Hanson, N. R. (1958). Patterns of Discovery. Cambridge, U.K.: Cambridge University Press.
Hart, H. L. A. and T. Honoré (1985). Causation in the Law (second ed.). Oxford, U.K.: Oxford University Press.
Hempel, C. G. (1965). Aspects of Scientific Explanation. New York: Free Press.
Henrion, M. and M. J. Druzdzel (1990). Qualitative propagation and scenario-based approaches to explanation of probabilistic reasoning. In P. P. Bonissone, M. Henrion, L. N. Kanal, and J. Lemmer (Eds.), Uncertainty in Artificial Intelligence 6, pp. 17–32. Amsterdam: Elsevier.
Hiddleston, E. (2005). Causal powers. British Journal for Philosophy of Science 56, 27–59.
Hitchcock, C. (1995). The mishap at Reichenbach Fall: singular vs. general causation. Philosophical Studies (3), 257–291.
Hitchcock, C. (2001). The intransitivity of causation revealed in equations and graphs. Journal of Philosophy XCVIII(6), 273–299.
Hitchcock, C. (2004). Do all and only causes raise the probability of effects? In J. Collins, N. Hall, and L. A. Paul (Eds.), Causation and Counterfactuals, pp. 403–418. Cambridge, MA: MIT Press.
Hitchcock, C. (2007). Prevention, preemption, and the principle of sufficient reason. Philosophical Review 116, 495–532.
Hitchcock, C. (2012). Events and times: a case study in meands-end metaphysics. Philosophical Studies 160, 79–96.
Hitchcock, C. (2013). What is the “cause” in causal decision theory? Erkenntnis 78, 129– 146.
Hitchcock, C. and J. Knobe (2009). Cause and norm. Journal of Philosophy 106, 587–612.
Honoré, A. (2010). Causation in the law. In E. N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy (Winter 2010 Edition). Available at http://plato.stanford.edu/archives/win2010/entries/causation-law.
Hoover, K. D. (2008). Causality in economics and econometrics. In L. Blume and S. Durlauf (Eds.), The New Palgrave: A Dictionary of Economics. New York: Palgrave Macmillan.
Hopkins, M. (2001). A proof of the conjunctive cause conjecture. Unpublished manuscript.
Hopkins, M. and J. Pearl (2003). Clarifying the usage of structural models for commonsense causal reasoning. In Proc. AAAI Spring Symposium on Logical Formalizations of Commonsense Reasoning.
Huber, F. (2013). Structural equations and beyond. Review of Symbolic Logic 6, 709–732.
Hume, D. (1748). An Enquiry Concerning Human Understanding. Reprinted by Open Court Press, LaSalle, IL, 1958.
Illari, P. M., F. Russo, and J. Williamson (Eds.) (2011). Causality in the Sciences. Oxford, U.K.: Oxford University Press.
Kahneman, D. and D. T. Miller (1986). Norm theory: comparing reality to its alternatives. Psychological Review 94(2), 136–153.
Kahneman, D. and A. Tversky (1982). The simulation heuristic. In D. Kahneman, P. Slovic, and A. Tversky (Eds.), Judgment Under Uncertainty: Heuristics and Biases, pp. 201–210. Cambridge/New York: Cambridge University Press.
Katz, L. (1987). Bad Acts and Guilty Minds. Chicago: University of Chicago Press.
Kim, J. (1973). Causes, nomic subsumption, and the concept of event. Journal of Philosophy LXX, 217–236.
Knobe, J. and B. Fraser (2008). Causal judgment and moral judgment: two experiments. In W. Sinnott-Armstrong (Ed.), Moral Psychology, Volume 2: The Cognitive Science of Morality, pp. 441–447. Cambridge, MA: MIT Press.
Kominsky, J., J. Phillips, T. Gerstenberg, D. Lagnado, and J. Knobe (2014). Causal suppression. In Proc. 36th Annual Conference of the Cognitive Science Society (CogSci 2014), pp. 761–766.
Kraus, S., D. Lehmann, and M. Magidor (1990). Nonmonotonic reasoning, preferential models and cumulative logics. Artificial Intelligence 44, 167–207.
Lagnado, D. A., T. Gerstenberg, and R. Zultan (2013). Causal responsibility and counterfactuals. Cognitive Science 37, 1036–1073.
Lewis, D. (1973a). Causation. Journal of Philosophy 70, 556–567. Reprinted with added “Postscripts” in D. Lewis, Philosophical Papers, Volume II, Oxford University Press, 1986, pp. 159–213.
Lewis, D. (1973b). Counterfactuals. Cambridge, MA: Harvard University Press.
Lewis, D. (1986a). Causal explanation. In Philosophical Papers, Volume II, pp. 214–240. New York: Oxford University Press.
Lewis, D. (1986b). Causation. In Philosophical Papers, Volume II, pp. 159–213. New York: Oxford University Press. The original version of this paper, without numerous postscripts, appeared in the Journal of Philosophy 70, 1973, pp. 113–126.
Lewis, D. (1986c). Events. In Philosophical Papers, Volume II, pp. 241–270. New York: Oxford University Press.
Lewis, D. (2000). Causation as influence. Journal of Philosophy XCVII(4), 182–197.
Lewis, D. (2004). Void and object. In J. Collins, N. Hall, and L. A. Paul (Eds.), Causation and Counterfactuals, pp. 277–290. Cambridge, MA: MIT Press.
Livengood, J. (2013). Actual causation in simple voting scenarios. Nous 47(2), 316–345.
Livengood, J. (2015). Four varieties of causal reasoning problem. Unpublished manuscript.
Livengood, J. and E. Machery (2007). The folk probably don’t think what you think they think: experiments on causation by absence. Midwest Studies in Philosophy 31, 107– 127.
Lombrozo, T. (2010). Causal-explanatory pluralism: how intentions, functions, and mechanisms influence causal ascriptions. Cognitive Psychology 61, 303–332.
Mackie, J. L. (1965). Causes and conditions. American Philosophical Quarterly 2/4, 261–264. Reprinted in E. Sosa and M. Tooley (Eds.), Causation, Oxford University Press, 1993.
Mackie, J. L. (1974). The Cement of the Universe. Oxford, U.K.: Oxford University Press.
Mandel, D. R. and D. R. Lehman (1996). Counterfactual thinking and ascriptions of cause and preventability. Journal of Personality and Social Psychology 71(3), 450–463.
McDermott, M. (1995). Redundant causation. British Journal for the Philosophy of Science 40, 523–544.
McGill, A. L. and A. E. Tenbrunsel (2000). Mutability and propensity in causal selection. Journal of Personality and Social Psychology 79(5), 677–689.
McGrath, S. (2005). Causation by omission. Philosophical Studies 123, 125–148.
Meliou, A., W. Gatterbauer, J. Y. Halpern, C. Koch, K. F. Moore, and D. Suciu (2010). Causality in databases. IEEE Data Engineering Bulletin 33(3), 59–67.
Meliou, A., W. Gatterbauer, K. F. Moore, and D. Suciu (2010). The complexity of causality and responsibility for query answers and non-answers. Proc. VLDB Endowment 4(1), 33–45.
Mellor, D. H. (2004). For facts as causes and effects. In J. Collins, N. Hall, and L. A. Paul (Eds.), Causation and Counterfactuals, pp. 309–323. Cambridge, MA: MIT Press.
Menzies, P. (2004). Causal models, token causation, and processes. Philosophy of Science 71, 820–832.
Menzies, P. (2007). Causation in context. In H. Price and R. Corry (Eds.), Causation, Physics, and the Constitution of Reality, pp. 191–223. Oxford, U.K.: Oxford University Press.
Menzies, P. (2014). Counterfactual theories of causation. In E. N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy (Spring 2014 Edition). Available at http://plato.stanford.edu/archives/spr2014/entries/causation-counterfactual/.
Mill, J. S. (1856). A System of Logic, Ratiocinative and Inductive (fourth ed.). London: John W. Parker and Son.
Moore, M. S. (2009). Causation and Responsibility. Oxford, U.K.: Oxford University Press.
Northcott, R. (2010). Natural born determinists. Philosophical Studies 150, 1–20.
O’Connor, A. (2012). When surgeons leave objects behind. New York Times. Sept. 24, 2012.
Pälike, H. (2013). Impact and extinction. Science 339(6120), 655–656.
Papadimitriou, C. H. and M. Yannakakis (1982). The complexity of facets (and some facets of complexity). Journal of Computer and System Sciences 28(2), 244–259.
Paul, L. A. (2000). Aspect causation. Journal of Philosophy XCVII(4), 235–256.
Paul, L. A. and N. Hall (2013). Causation: A User’s Guide. Oxford, U.K.: Oxford University Press.
Pearl, J. (1988). Probabilistic Reasoning in Intelligent Systems. San Francisco: Morgan Kaufmann.
Pearl, J. (1989). Probabilistic semantics for nonmonotonic reasoning: a survey. In Proc. First International Conference on Principles of Knowledge Representation and Reasoning (KR ’89), pp. 505–516. Reprinted in G. Shafer and J. Pearl (Eds.), Readings in Uncertain Reasoning, pp. 699–710. San Francisco: Morgan Kaufmann, 1990.
Pearl, J. (1998). On the definition of actual cause. Technical Report R-259, Department of Computer Science, University of California, Los Angeles, Los Angeles, CA.
Pearl, J. (1999). Probabilities of causation: three counterfactual interpretations and their identification. Synthese 121(1/2), 93–149.
Pearl, J. (2000). Causality: Models, Reasoning, and Inference. New York: Cambridge University Press.
Pearl, J. (2009). Causal inference in statistics. Statistics Surveys 3, 96–146.
Regina v. Faulkner (1877). Court of Crown Cases Reserved, Ireland. In 13 Cox Criminal Cases 550.
Riker, W. H. and P. C. Ordeshook (1968). A theory of the calculus of voting. American Political Science Review 25(1), 25–42.
Robinson, J. (1962). Hume’s two definitions of “cause”. The Philosophical Quarterly 47(12), 162–171.
Salmon, W. C. (1970). Statistical explanation. In R. Kolodny (Ed.), The Nature and Function of Scientific Theories, pp. 173–231. Pittsburgh, PA: University of Pittsburgh Press.
Salmon, W. C. (1984). Scientific Explanation and the Causal Structure of the World. Princeton, N.J.: Princeton University Press.
Schaffer, J. (2000a). Causation by disconnection. Philosophy of Science 67, 285–300.
Schaffer, J. (2000b). Trumping preemption. Journal of Philosophy XCVII(4), 165–181. Reprinted in J. Collins and N. Hall and L. A. Paul (Eds.), Causation and Counterfactuals. Cambridge, MA: MIT Press, 2002.
Schaffer, J. (2004). Causes need not be physically connected to their effects. In C. Hitchcock (Ed.), Contemporary Debates in Philosophy of Science, pp. 197–216. Oxford, U.K.: Basil Blackwell.
Schaffer, J. (2012). Disconnection and responsibility. Legal Theory 18(4), 399–435.
Schumacher, M. (2014). Defaults, normality, and control. Unpublished manuscript.
Schupbach, J. (2011). Comparing probabilistic measures of explanatory power. Philosophy of Science 78, 813–829.
Scriven, M. J. (1959). Explanation and prediction in evolutionary theory. Science 130, 477–482.
Shafer, G. (2001). Causality and responsibility. Cardozo Law Review 22, 101–123.
Shimony, S. E. (1991). Explanation, irrelevance and statistical independence. In Proc. Ninth National Conference on Artificial Intelligence (AAAI ’91), pp. 482–487.
Shoham, Y. (1987). A semantical approach to nonmonotonic logics. In Proc. 2nd IEEE Symposium on Logic in Computer Science, pp. 275–279. Reprinted in M. L. Ginsberg (Ed.), Readings in Nonmonotonic Reasoning, pp. 227–250. San Francisco: Morgan Kaufman, 1987.
Simon, H. A. (1953). Causal ordering and identifiability. In W. C. Hood and T. C. Koopmans (Eds.), Studies in Econometric Methods, Cowles Commission for Research in Economics, Monograph No. 14, pp. 49–74. New York: Wiley.
Sipser, M. (2012). Introduction to Theory of Computation (third ed.). Boston: Thomson Course Technology.
Sloman, S. A. (2009). Causal Models: How People Think About the World and Its Alternatives. Oxford, U.K.: Oxford University Press.
Smith, A. (1994). An Inquiry into the Nature and Causes of the Wealth of Nations. New York, NY: Modern Library. Originally published in 1776.
Sober, E. (1984). Two concepts of cause. In PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association, pp. 405–424.
Sosa, E. and M. Tooley (Eds.) (1993). Causation. Oxford Readings in Philosophy. Oxford, U.K.: Oxford University Press.
Spirtes, P., C. Glymour, and R. Scheines (1993). Causation, Prediction, and Search. New York: Springer-Verlag.
Spohn, W. (1988). Ordinal conditional functions: a dynamic theory of epistemic states. In W. Harper and B. Skyrms (Eds.), Causation in Decision, Belief Change, and Statistics, Volume 2, pp. 105–134. Dordrecht, Netherlands: Reidel.
Stalnaker, R. C. (1968). A theory of conditionals. In N. Rescher (Ed.), Studies in Logical Theory, pp. 98–112. Oxford, U.K.: Blackwell.
Stockmeyer, L. J. (1977). The polynomial-time hierarchy. Theoretical Computer Science 3, 1–22.
Strevens, M. (2008). Comments on Woodward, Making Things Happen. Philosophy and Phenomenology 77(1), 171–192.
Strevens, M. (2009). Depth. Cambridge, MA: Harvard Univesity Press.
Strotz, R. H. and H. O. A. Wold (1960). Recursive vs. nonrecursive systems: an attempt at synthesis. Econometrica 28(2), 417–427.
Suppes, P. (1970). A Probabilistic Theory of Causality. Amsterdam: North-Holland.
Sytsma, J., J. Livengood, and D. Rose (2012). Two types of typicality: rethinking the role of statistical typicality in ordinary causal attributions. Studies in History and Philosophy of Biological and Biomedical Sciences 43, 814–820.
van Fraassen, B. C. (1980). The Scientific Image. Oxford, U.K.: Oxford University Press.
Watson v. Kentucky and Indiana Bridge and Railroad (1910). 137 Kentucky 619. In 126 SW 146.
Weslake, B. (2015). A partial theory of actual causation. British Journal for the Philosophy of Science. To appear.
Wolff, P., A. K. Barbey, and M. Hausknecht (2010). For want of a nail: how absences cause events. Journal of Experimental Psychology 139(2), 191–221.
Woodward, J. (2003). Making Things Happen: A Theory of Causal Explanation. Oxford, U.K.: Oxford University Press.
Woodward, J. (2006). Sensitive and insensitive causation. Philosophical Review 115, 1–50.
Woodward, J. (2014). Scientific explanation. In E. N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy (Winter 2014 edition). Available at http://plato.stanford.edu/archives/win2014/entries/scientific-explanation/.
Woodward, J. (2016). The problem of variable choice. Synthese. To appear.
Wright, S. (1921). Correlation and causation. Journal of Agricultural Research 20, 557– 585.
Zhang, J. (2013). A Lewisian logic of causal counterfactuals. Minds and Machines 23(1), 77–93.
Zimmerman, M. (1988). An Essay on Moral Responsibility. Totowa, N.J.: Rowman and Littlefield.
Zultan, R., T. Gerstenberg, and D. Lagnado (2012). Finding fault: causality and counterfactuals in group attributions. Cognition 125, 429–440.
AC1, 23–26, 28, 32, 54, 57, 60, 65, 68, 160, 161, 206
AC2, 23, 25, 28, 32, 54, 57, 60, 62, 63
AC2(a), 23–26, 28, 32, 54, 57, 59, 60, 62–65, 68–70, 81, 82, 86, 89, 155, 209
AC2(am), 25, 26, 35, 54, 57, 65, 68–70, 81, 86, 97, 114, 155, 160, 161
AC2(bo), 24–26, 28, 32, 35, 37, 40, 53, 54, 57–59, 61–63, 65, 68, 69, 75, 85, 89, 116, 117, 155, 206
AC2(bu), 25, 26, 28, 32, 35, 37, 53, 54, 57–63, 65, 75, 76, 85, 116, 117, 155, 206
AC2(c), 75
AC2+(a), 81, 82, 85, 86, 89, 93, 94, 96, 97, 101, 120
AC2+(am), 81, 84–86, 101, 114, 120
AC3, 23, 24, 26–28, 32, 54, 57, 60, 65, 68, 160, 161, 206
accountability, 204, 205, 211, 212
actual world, see world
acyclic causal model, see causal model, recursive
Adams, D., 139
Adams, E., 103
Alechina, N., 184
algebraic conditional plausibility measure, see plausibility measure
Alicke, M., 103
Alvarez, L. W., 5
Alvarez, W., 5
anti-symmetric relation, 17, 80
Asaro, M., 5
axiom system, 154
Balke, A., 74
Barbey, A. K., 104
Baumgartner, M., 6
Bayesian network, 72, 140–142, 147, 167
Beckers, S., ix, 105
Beebee, H., 103
Bell, J. S., 7
best witness, 86, 87, 94, 96, 98
binary model, see causal model, binary
blame, 1, 41, 46, 53, 56, 75, 94, 99, 169–171, 173–179, 183–185, 188, 195, 203, 204
Bloom, D., 103
Box, G. E. P., 107
but-for cause, 3, 4, 7, 12, 23, 26, 29, 36, 38–41, 43–46, 53, 55, 58, 64, 66–68, 73, 83, 87, 92, 93, 96, 100, 109, 110, 112, 171, 172, 177, 178, 181, 185
bystander effect, 178, 179, 183
Casati, R., 72
causal formula, 20, 21, 56, 155, 158, 188
causal graph, see causal network
causal model, 13, 15, 16, 18, 19, 21, 35, 38, 41–45, 47–51, 66, 71
binary, 154
extended, 81, 84, 90, 119–122, 132, 139, 145, 150, 159
insufficiently expressive, 108, 109, 124, 125, 194
recursive, 17, 21, 34, 56, 57, 67, 70, 75, 127, 155, 156, 164
causal network, 16, 18, 30, 34, 36, 40, 41, 45, 60, 62, 63, 66, 70, 72, 100, 141, 142, 144, 145, 178, 194
causal path, 24, 45, 46, 61–64, 66–70, 75, 115
causal setting, 21, 23, 38, 46, 48, 54, 66, 97, 169, 170, 173–175, 178–181, 185, 188, 199, 200, 206
Chekov, A., 77
Chockler, H., ix, 168, 183, 184, 208, 210, 212, 213
Chu, F., 186
closest-word semantics for counterfactuals, 71
co-NP, see computational complexity, co-NP
compact representation, 140–144
complete assignment, 57, 79, 122
complete axiomatization, 157, 162
complexity, see computational complexity
computational complexity, 140, 151–154, 157, 158, 160, 161, 166–168, 184, 211
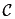 -complete, 153
-complete, 153
 -hard, 152
-hard, 152
co-NP, 152
complexity class, 151
co-NP, 151, 152, 157, 158, 160
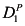 , 168
, 168
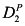 -complete, 153
-complete, 153
EXPTIME, 151
NP, 160
NP-complete, 154, 157, 161, 166, 168, 210
NP-hard, 152
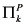 , 152
, 152
polynomial hierarchy, 152, 153, 168
polynomial time, 151–153, 160, 161, 166, 207, 210
PSPACE, 151
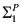 , 152
, 152
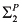 , 152
, 152
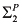 -complete, 153
-complete, 153
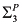 , 152
, 152
condition, 19
conditional independence, see independence (of variables)
conditional plausibility measure, see plausibility measure
conjunctive model of forest fire, see forest-fire example, conjunctive model
conjunctive query, see query, conjunctive
conservative extension, 115–123, 127–133, 135
consistent with axiom system, 154, 162, 168
context, 17, 19, 21, 24–26, 28–32, 34–36, 38, 39, 42–44, 46, 51, 53–57, 59–63, 69, 70, 74, 75, 174
contingency, 4, 23, 24, 28, 32, 36, 39, 40, 57, 59, 60, 62, 88, 90–92, 109–112, 124, 134, 191, 210
Cook, S., 168
counterfactual, 2, 3, 6, 7, 15, 23, 43, 53, 55, 62, 71, 142, 188, 201, 203, 207, 212, 213
counterfactual dependence, see dependence (of one variable on another)
criticality, 185
Crowe, R., 187
Cushman, F., 103
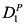 , see computational complexity,
, see computational complexity, 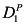
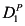 -complete, see computational complexity,
-complete, see computational complexity, 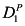 -complete
-complete
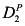 -complete, see computational complexity,
-complete, see computational complexity, 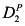 -complete
-complete
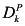 , see computational complexity,
, see computational complexity, 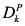
Das, S., 107
Davidson, D., 136
deductive-nomological model (for explanation), 188, 201
default, 77, 80, 82, 102, 110, 149, 150
default rule, see default
degree of blame, see blame
degree of responsibility, see responsibility
dependence (of one variable on another), 14–19, 21, 31, 34, 43, 45, 47, 56, 62, 66, 67, 72, 124, 126, 142, 148, 171, 172
disjunctive explanation, see explanation, disjunctive
disjunctive model of forest fire, see forest-fire example, disjunctive model
Draper, N. R., 107
Druzdzel, M. J., 202
Dubois, D., 103
Einstein, A., 23
endogenous variable, 108
endogenous variable, 13, 17–21, 23, 24, 28, 30, 32, 34, 38, 47, 49, 50, 56, 57, 62, 66, 67, 79–82, 84, 85, 87–94, 98, 100, 101, 105, 107–109, 111, 117, 120–122, 127, 131, 132, 134, 144, 153, 155, 161–163, 165, 166, 172, 191, 194, 195, 197, 200, 204, 205
epistemic state, 170, 173–175, 184, 187–189, 199, 201
equations, see structural equations
exogenous variable, 13, 15–20, 28, 30, 47–49, 56, 57, 66, 79–82, 85, 87, 91–94, 98, 107, 108, 117, 122, 125, 127, 134, 135, 145, 155, 161, 166, 194, 200, 204
explanandum, 187, 188, 192, 197, 199
explanation, 56, 187–203, 210, 213
disjunctive, 190, 191, 193, 198
nontrivial, 189, 190, 195, 197, 199, 200
explanatory power, 197–199, 202
EXPTIME, see computational complexity, EXPTIME
extended causal model, see causal model, extended, 171
extends, see witness extends another witness
Fagin, R., 168
Faigman, D. L., 6
Falcon, A., 6
Federer, R., 169
Feigenbaum, J., 212
Fenton-Glynn, L., 74
Fienberg, S. E., 6
Fitelson, B., 74
forest-fire example, 10, 14–19, 23, 28–29, 54–56, 61, 63–64, 71, 80, 82, 84, 104, 107, 125–126, 145–146, 172, 173, 189–190, 193
conjunctive model, 11, 14–16, 28, 54, 55, 145, 172, 173, 190
disjunctive model, 11, 14, 16, 21, 22, 28, 30, 54, 56, 63–64, 88, 113–114, 145–146, 150, 154, 172, 173, 189–190, 193, 197
fire in May or June, 190–192, 198
Frick, J., 74
Friedman, N., 167
Gatterbauer, W., 212
Geffner, H., 103
Gerstenberg, T., ix, 6, 75, 105, 185
Goldberger, A. S., 70
Goldman, A. I., 184
Goldszmidt, M., 103
Gomes, C. P., 168
Good, I. J., 6
Goodman, N. D., 75
Goodman, N. D., 6
graded causality, 86, 87, 89, 98–101, 105, 169, 170, 178, 181
Groce, A., 213
Grumberg, O., 213
H-account, 75
Haavelmo, T., 70
Hall, N., 6, 71–75, 102, 104, 105, 135, 136
Halpern, D., v
Halpern, G., v
Halpern, J. Y., 3, 6, 22, 70–76, 102–105, 136, 167, 168, 183, 184, 186, 201, 202, 212, 213
Halpern, S., v
Hanson, N. R., 136
Hausknecht, M., 104
Hawking, S., 203
Henrion, M., 202
Hiddleston, E., 104
Hitchcock, C., ix, 6, 71–75, 102–105, 136, 167
Hoffman, D., ix
Hoover, K. D., 7
Huber, F., 136
Illari, P. M., 7
independence (of variables), 15, 17, 18, 34, 124, 127, 128, 140–145, 150, 159, 165, 167
insufficiently expressive (causal model), see causal model, insufficiently expressive
intervention, 14, 15, 21, 32, 47, 81, 108, 124, 125, 127, 137, 155, 205
Jaggard, A. D., 212
Kahneman, D., 103
Katz, L., 72
Kautz, H., 168
Kim, J., 136
Knobe, J., 79, 86, 103, 104, 185
Kominsky, J., 185
Konigsburg, E. L., 187
Kraus, S., 103
Kripke structure, 207, 208, 210
Kupferman, O., 213
Lagnado, D., ix, 6, 75, 105, 185
language, 9, 10, 15, 18, 20, 22, 26, 34, 151, 152, 154, 155, 157, 158, 160–162, 206
Lehman, D. R., 103
Lehmann, D., 103
Lewis, D., 7, 71, 73–75, 103–105, 136, 201
Livengood, J., ix, 5, 104, 105
Logan, B., 184
Lombrozo, T., 212
Lorenz, E., 9
Machery, E., 104
Magidor, M., 103
Mandel, D. R., 103
maximal consistent set, 162
maximum a posteriori (MAP) approach, 202
Maxton, R., ix
McGill, A. L., 103
McGrath, S., 104
Meliou, A., 212
Mellor, D. H., 72
Merovingian, 9
Michel, H., 5
Mill, J. S., 104
Miller, D. T., 103
minimal counterexample, 209
model, see causal model
model checking, see program verification
montone query, see query, monotone
Moore, K. F., 212
moral responsibility, 170, 171, 184
Moses, Y., 168
nonrecursive causal model, see causal model, nonrecursive
nontrivial explanation, see explanation, nontrivial
normality, 4, 19, 32, 38, 39, 56, 64, 75, 77, 79–105, 107–109, 114, 119, 120, 122, 126, 127, 132–135, 139, 143, 144, 170, 171, 180–183, 185, 197, 203, 204, 211, 212
normality ordering, 80–85, 88, 93, 94, 96, 97, 99, 102–105, 107, 108, 119–122, 132, 134, 135, 139, 142–145, 148–150, 212
respects the equations, 120–122, 134, 135
Northcott, R., 74
NP, see computational complexity, NP
NP-complete, see computational complexity, NP-complete
O'Connor, A., 73
omissions as causes, 38, 72, 82–83, 103, 104
Ordeshook, P. C., 185
overdetermination, 29
P (polynomial time), see computational complexity, P (polynomial time)
Pälike, H., 5
Papadimitriou, C. H., 168
partial (pre)order, 17, 18, 67, 70, 80, 81, 97, 103, 127, 142–145, 147, 150, 159, 165, 183
Paul, L. A., ix, 6, 71–74, 135
Pearl, J., ix, 3, 6, 7, 22, 70–76, 102, 103, 105, 168, 201, 202
Philips, J., 185
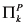 , see computational complexity,
, see computational complexity, 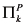
plausibility, see plausibility measure
plausibility measure, 143–146, 148–150, 158–160, 167, 183, 186
algebraic conditional, see plausibility measure
polynomial hierarchy, see computational complexity, polynomial hierarchy
polynomial time, see computational complexity, polynomial time
possibility measure, 103
possible world, see world
potentially helpful, 209
Prade, H., 103
trumping, 73
preferential structure, 103
primitive event, 20–22, 56, 57, 128, 199
probability of sufficiency, 75
process theories of causation, 201
provable (in axiom system), 154, 155, 157, 162
PSPACE, see computational complexity, PSPACE
conjunctive, 207
monotone, 206
ranking function, 97, 103, 144
recursive causal model, see causal model, recursive
reduced, 152
refinement, 213
reflexive relation, 17
regularity definition (of causality), 2, 6
respects the equations, see normality ordering, respects the equations
responsibility, 1, 29, 30, 40, 41, 169–185, 203–205, 207, 211, 213
Rickover, H. G., 169
right weakening, 41
Riker, W. H., 185
Robinson, J., 6
rock-throwing example, 3, 4, 7, 23, 24, 30–32, 34, 35, 47–49, 51–53, 55, 59, 60, 70, 72, 84, 85, 89, 97, 98, 105, 107–109, 114, 115, 117, 119, 122, 124, 141, 153, 172–174, 184
Rosen, D., 74
Russo, F., 7
Sabharwal, A., 168
satisfiable, 151, 155, 157, 160–162, 165–167
Scheines, R., 72, 73, 136, 167
Schumacher, M., 105
Schupbach, J., 202
Scriven, M. J., 202
Selman, B., 168
Shafer, G., 184
Shimony, A., 202
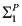 , see computational complexity,
, see computational complexity, 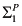
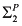 , see computational complexity,
, see computational complexity, 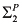
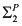 -complete, see computational complexity,
-complete, see computational complexity, 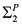 -complete
-complete
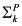 , see computational complexity,
, see computational complexity, 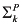
signature, 13, 153, 155, 157, 166
Simon, H. A., 70
Sinnott-Armstrong, W., 103
Sipser, M., 168
Sloman, S. A., 7
Smith, A., 7
Sosa, E., 201
sound axiomatization, 155, 157, 162
Stalnaker, R. C., 71
statistical relevance model (for explanation), 188, 201
statisticians' notation, 22, 24, 25, 66, 155, 156, 162
Stockmeyer, L. J., 168
strong causality, 75
Strotz, R. H., 75
structural equations, 4, 10, 13–15, 18, 19, 21, 25, 31, 34, 41–44, 47–49, 53, 56, 57, 59, 68, 70–73, 79, 80, 84, 87–89, 93, 95, 96, 107–113, 115, 120–122, 125, 127, 129–135, 139–142, 144–146, 148–150, 153, 156, 157, 161–167, 173, 178, 195, 201, 203, 205, 206, 212
substitution instance, 156
Suciu, D., 212
sufficient cause, 54–56, 75, 82, 188–196, 199–201, 212
Suppes, P., 74
Sytsma, J., 104
Tenbrunsel, A. E., 103
token causality, 1
Tooley, M., 201
total (pre)order, 70, 80, 81, 103, 104
transitive relation, 17
transitivity of causality, 41–46, 155
trivial explanation, see explanation, nontrivial
trumping preemption, see preemption, trumping
tuple (in database), 205–207, 211
Tuttle, M. R., 74
Tversky, A., 103
typicality, 4, 77–82, 85, 89, 93–96, 98, 103, 143, 144, 146, 148–150, 154
valid, 151, 155, 157, 158, 162
van Fraassen, B., 73
Vardi, M. Y., 168
variable
binary, 10–12, 38, 45, 58, 63, 139–141, 150, 154, 206, 207, 209
variable takes on value other than that specified by equations, 120, 133
Varzi, A., 72
Virgil, 1
voting examples, 10, 16, 29, 30, 54, 59–62, 75, 83, 91, 92, 105, 112, 113, 142, 154, 169, 170, 172, 173, 177–182, 184, 185, 190
Watson v. Kentucky and Indiana Bridge and Railroad, 94, 105
Weslake, B., 136
Williamson, J., 7
Williamson, T., 184
Wimberly, F., 71
witness, 25, 26, 28, 29, 39, 60, 62–65, 68–70, 82, 84–86, 128–130, 132–135, 171–173, 180–182, 185, 206, 207
witness event, 98
witness extends another witness, 128, 129
witness world, 85–87, 89, 90, 93, 94, 96, 98, 99, 101, 103, 114, 120, 128, 180, 182, 192
Wold, H. O. A., 75
Wolff, P., 104
Woodward, J., 71, 75, 105, 136, 201
world, 79–87, 89–94, 96–99, 101, 103, 105, 109, 119, 120, 122, 126, 132, 134–136, 139, 140, 142–150
Wright, R. N., 212
Wright, S., 70
Yadgar, A., 213
Yannakakis, M., 168
Zimmerman, M., 184