Lazy Code Motion
Code motion optimizations shift computations around a control-flow graph
(CFG) in order to avoid redundant computation, reduce code size, or save
resources. Loop invariant code motion, for example, identifies expressions
computed within loops which have the same value from iteration to iteration and
hoists them out of the loop so that they are computed only once. Common
subexpression elimination can also be viewed as a code motion
optimization: rather than computing a subexpression e twice in expressions
f(e) and g(e), compute it once and store it in a termporary register.
Lazy code motion unifies and improves upon several forms of code motion including loop invariant code motion and common subexpression elimination. It is termed lazy to contrast with earlier approaches to unified code motion which placed compuatations as early as possible. Perhaps this will make more sense if we take a look at an example. I adapted the following from Wikipedia.
main {
five: int = const 5;
br some_condition compute do_nothing;
compute:
y: int = add x five;
jmp done;
do_nothing:
jmp done;
done:
z: int = add x five;
ret;
}
If some_condition holds then x + 5 whill be computed twice, but if it is
false then the computation only happens once. This is a "partial redundancy,"
and traditional common subexpression elimination will not fix it. A good global
code motion analysis will fix it, emitting code that looks something like this.
main {
five: int = const 5;
br some_condition compute do_nothing;
compute:
tmp: int = add x five;
y: int = id tmp;
jmp done;
do_nothing:
tmp: int = add x five;
jmp done;
done:
z: int = tmp;
ret;
}
Now all paths through the program include only one computation of x+5. This is
optimal code, at least along that dimension, and a realistic result to expect from
partial redundancy elimination or lazy code motion. So what makes lazy code
motion different from eager alternatives?
Register pressure
When lowering IR code to assembly, compilers have to allocate storage for a finite but unbounded number of variables in an architecture with a finite and fixed number of registers. If there are more variables than registers, some of them are going to end up on the stack. "Spilling" to the stack is costly--memory is slower than registers.
Earlier passes in the compiler should try to minimize the number of spills introduced during register allocation. The precise number of spills introduced into a program depends on the register allocation algorithm in use, which makes designing optimizations against this metric something of a fool's errand. Lazy code motion looks to a more understandable proxy metric known as register pressure. Register pressure, for each program point, is the number of live variables at that point as determined by a standard liveness analysis.
Eager code motion moves variable definitions (computations) further away from their uses, which lengthens their live ranges. The resulting register pressure can easily claw back any performance gains due to code motion. Rather than put computations as early as possible, lazy code motion moves them down to the a later program point that still avoids redundant computation. In fact, one paper proves that lazy code motion places computations "as late as possible" ([1], Theorem 3), but this wording is misleading outside its original context. The algorithm actually uses a static analysis to identify possible safe moves and then selects the latest options. This is not always "as late as possible" because in general the static analysis will underapproximate the set of possible safe moves.
Implementation
I implemented lazy code motion in OCaml. Since the existing Bril infrastructure is written in Python and TypeScript, I had to implement Bril JSON parsing and design data structures for representing control flow graphs. The open source OCamlgraph library helped with this. It includes excellent generic graph data structures and a framework for implementing dataflow analyses over graphs.
There were some mismatches between the dataflow analyses presented by Drechsler
et al. [1] and the OCamlgraph dataflow framework. The biggest issue was that
the OCamlgraph framework made it hard to refer to results of other dataflow
passes in later ones. I worked around this by tagging every basic block in the
CFG with a map of "attributes" and writing OCaml functors like MakeDataflow
that require their input module to include an attr_name field. When you run
a dataflow analysis created with MakeDataflow, it saves the results of the
analysis at each basic block into the attributes map under the attr_name key.
The analyses were easy to write down once there was structure in place for defining them. For example, here is the definition of an available expressions analysis from the paper:
let avail_out (_, block_attrs) avail_in =
Bitv.bw_or
(Bitv.bw_and
(Cfg.Attrs.get block_attrs "transparent")
avail_in)
(Cfg.Attrs.get block_attrs "computes")
module AvailabilityIn =
MakeDataflow
(struct
let attr_name = "availability_in"
let direction = Graph.Fixpoint.Forward
let init _ =
EXPRS.build ~f:(fun _ -> false)
let analyze (src, _, _) src_avail_in =
avail_out src src_avail_in
end)
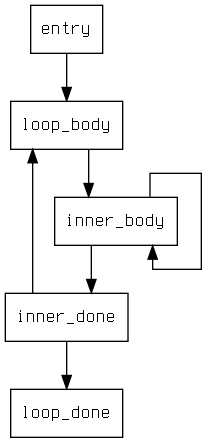
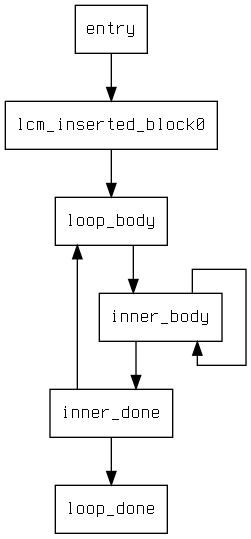
I implemented a CFG printer using the OCamlgraph Graphviz backend so that
I could debug the optimization's changes to CFGs directly, rather than staring
at pretty printed output. Here's the result of running the optimization on
tests/lcm/simple, a nested loop benchmark. There's a way to include the
instructions from each block inside the nodes, but for this example that makes
it hard to follow. There is a loop invariant computation in inner_body that
lazy code motion hoists to lcm_inserted_block0.
Limitations
I implemented the full lazy code motion optimization, but there were some issues. The optimization expects lexically equal expressions to always be stored into the same pseudoregister. There may be adaptations of the dataflow analyses in later work to weaken this assumption, but I introduced a conservative code rewriting pass that made sure expressions went into a uniquely named temporary. This increases register pressure and introduces extraneous move instructions to retrieve computed values from temporaries. A more clever rewriting pass might be able to ameliorate these costs.
On the other end of the optimization, the computation placement algorithm is inefficient. Lazy code motion places computations on edges of the CFG, which means stitching new basic blocks into edges. While they are neccessary in general, on many edges an inserted basic block could be safely merged with its predecessor or successor block. This could have performance benefits because it would reduce the number of jumps. Similarly the pretty-printer for CFGs does not omit jumps where fall-through would work--this seems like a minor detail but could have performance or code size implications. Both of these issues could be addressed with a simplification pass to be run after lazy code motion.
Evaluation
I instrumented the interpreter to count operations and computations.
A computation is any instruction that computes the value of an expression. An
operation is any instruction at all, including control flow and return
instructions. Many of the programs in the examples and test directories are
either a single basic block or include no computations, so I excluded them from
this evaluation because the optimization doesn't do anything to them.
| program | ops (before lcm) | computations (before lcm) | ops (after lcm) | computations (after lcm) |
|---|---|---|---|---|
| test/lcm/dont-hoist-thru-loop | 8 | 1 | 11 | 1 |
| test/lcm/two-blocks | 5 | 1 | 8 | 1 |
| test/lcm/hoist-thru-loop | 412 | 303 | 617 | 203 |
| test/lcm/simple | 1217 | 906 | 1925 | 605 |
| examples/lvn_test/nonlocal | 7 | 3 | 12 | 3 |
| examples/dom_test/loopcond | 117 | 46 | 165 | 46 |
| examples/df_test/cond | 9 | 1 | 12 | 1 |
| examples/df_test/fact | 62 | 25 | 89 | 25 |
Since lazy code motion is designed to avoid redundant computations of expressions, the number of computations never increases after optimization. It looks like the overhead of the conservative temporary allocation strategy and basic block insertion impacts the total number of computations negatively by adding moves and jumps respectively. Loopy benchmarks (simple, hoist-thru-loop) exhibit significant speedups due to computations being hoisted out of their loops.
Bibliography
- Drechsler, K.-H., Stadel, M. P. A variation of Knoop, Rüthing, and Steffen's Lazy Code Motion. SIGPLAN Notices 28, 5, (1993), 29-38.
- Knoop, J., Rüthing, O., Steffen, B. Lazy code motion. SIGPLAN Notices 27, 7, (1992), 224-234.