Bril Phase Selection and Ordering
Background
Modern compilers are often organized in terms of independent "passes". That is, a compiler will consist of tens or even hundreds of optimization passes that each do a clearly defined task. Along with these many passes, however, comes the problem of ordering them. For example, it isn't obvious whether one should run constant folding or copy propagation first. Although some of these may have well defined answers, it's likely that one can find an example in which the ordering performs poorly.
We set out to try and build a ML-based phase selection/ordering system. Due to some amount of problems/discoveries, we ended up only analyzing the effects of different orders and generating an optimal sequence of optimizations.
Design Overview
Optimizations
To set up the phase ordering task, we selected and implemented several optimization passes:
-
For Dead Code Elimination (DCE), we used the given implementation directly.
-
For data flow analysis based optimization passes, we implemented Copy Propagation and Constant Folding, as defined in the lecture. Each pass will gather data flow analysis information first then modify the instructions in place.
-
For control flow graph optimizations, we implemented Branch Removal, Unreachable Code Elimination, CFG cleaning and Tail Merging. We refer to this slide for more details.
-
Branch Removal
If we can decide the guard value to be true or false, then we can eliminate one of the two branches accordingly.
-
Unreachable Code Elimination(UCE)
The basic blocks unreachable from the entry block will be removed.
-
CFG cleaning
We can simplify CFG by several transformations that eliminate useless edges and combine some basic blocks. Specifically, we can 1) replace a br instruciton with two identical destination to a jmp instruciton; 2) merging empty blocks; 3) merging two blocks with only one edge in between under some cases.
-
Tail Merging
If the predecesssor or successors share a same section of code in the end or begining correspondingly, we can change the jump to reuse the same segment of code.
-
In general, the optimization we selected are tailored for the simple structure of Bril, which has a lot of contant calculation and branches that do not allow falling through. Passes like DCE and UCE will likely to remove more codes, but other passes might or might not generate new opportunities for DCE and UCE. Thus we need to order passes properly to obtain best performance, especially under the case where we can only apply limited number of passes.
Random Program Generator
In order to analyze programs in Bril, one obstacle was that we didn't have a large enough corpus of code to analyze. To do statistical analysis or any kind of optimization techniques, we need a substantial training set to evaluate our ordering methods.
To create this training set, we created a random Bril program generator. Our program generator evaluates each decision independently, and doesn't take any care to preserve program wide structure. We follow this flow chart at each step.
- First, we randomly chose whether we want to insert a binary operation, a constant, or an id.
- Next, given the instruction type, we decide whether it should be a boolean or an integer.
- Finally, we choose whether this instruction should write to a new identifier or an already existing identifier. If it's an already existing identifier we uniformly choose one from all the identifiers of the correct type.
One thing that we've ignored so far is control flow. Considering that several of our optimizations are control flow optimizations, we clearly need to handle them somehow. However, introducing arbitrary control flow is fairly tricky. For example, we may construct non-terminating programs, which make evaluating them/checking our optimizations for bugs tricky.
Thus, we settled on constructing a Directed Acyclic Graph. Every fixed interval, we insert a label. In addition to that label, we have a chance of adding a jump/branch to a succeeding label.
We note that there are a lot of hand set probabilities in this generation process that have the ability to heavily affect the types of programs generated. For example, introducing a lot of control flow makes it more difficult for other optimizations to be applied. Thus, we select a mix of random constants.
Phase Ordering Analysis
So, first of all, how much does the phase ordering even matter? To evaluate the effectiveness of our optimizations, we will use # of instructions as a proxy.
We will use three different test sets for this. One where we have a lot of control flow, one with no control flow, and one with intermediate control flow. These will be called CFLow, CFMid, and CFHigh.
Then, we apply 200 random permutations of the 7 optimizations mentioned above. We record the worst and the best performing permutation, and report that here.
| Dataset | Avg Low | Avg High | Avg Ratio |
|---|---|---|---|
| CFLow | 18.7 | 26.3 | .72 |
| CFMid | 34.0 | 39.0 | .87 |
| CFHigh | 52.7 | 54.7 | .96 |
As we can see, especially on the programs with low amounts of control flow, there can be a huge difference between the best and worst permutation.
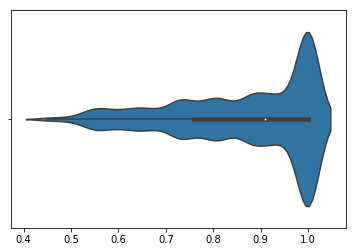
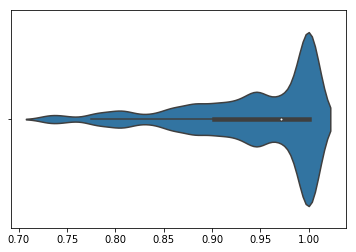
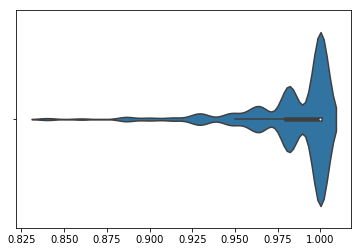
However, merely the min and max does not provide much information about how the distribution of possible permutations performs. To show that, we will normalize all permutation performances by the worst performing permutations and plot the distribution as a violin plot. We see that there is a tail of permutations that performs substantially better than the majority of permutations, many of which perform as bad as the worst permutation.
CFLow:
CFMid:
CFHigh:
Phase Ordering Heuristics
However, questions remain about the nature of the good performing permutations. Is there a single true permutation? Or does the ideal permutation vary among programs? To answer that, we generated random permutations and evaluated them across all 3 datasets. We report the percentage (# instrs of optimized program/# instrs of unoptimized program) of the best single permutation across a given dataset, the average percentage for optimizing the permutation per program, and the percentage for the best overall permutation across all three datasets.
| Dataset | Best Permutatation | Best Individual Permutation | Overall Permutation |
|---|---|---|---|
| CFLow | 35.81 | 35.32 | 36.15 |
| CFMid | 59.28 | 59.24 | 59.28 |
| CFHigh | 77.60 | 77.54 | 77.61 |
Somewhat disappointingly, we find that there are permutations that always perform very close to the optimal permutation for any program. On average, the optimal permutations reduced the code length to 57.68% of the original code length.
Doing so, we also find that there are many permutations with the best performance as the best permutation (selected by best average performance across all 3 datasets). We were curious if there was essentially some subset of the optimizations that mattered. We analyze all of the "optimal" permutations for common subsequences, and find that all of the optimal permutations had the following order of permutations:
- Copy Propagation
- Constant Folding
- Branch Removal
- Dead Code Elimination
We find that for our datasets, these are the only optimizations that matter. Removing the other 3 optimizations still provides the same performance across our dataset.
However, note that per program, there is still occasionally performance improvements to be found. Of our 150 random programs, there are 10 programs in which we can find a better order than the fixed dataset wide one. We're unable to isolate any particular pattern these programs/permutations have.
Future Work
Originally we were interested in using ML to choose optimization orders. However, because of how effective a fixed optimization order is, we decided that we were unlikely to get substantive improvements from a ML based ordering system. We suspect that this is due to the low amount of optimizations we have, as well as the lack of more "ambiguous" optimizations. Optimizations like constant folding or dead code elimination always improves performance of code (we think...). Thus, it's possible that there is a fixed optimization order that achieves almost optimal performance. However, the implementation cost of adding more optimization passes (including verifying their correctness) limited us to only 7 optimizations.
Future work would include more optimization passes. If adding more optimization passes gave more ambiguity in the optimization ordering, we could then explore program specific orderings.
Another aspect of optimization passes that we completely ignored is the fact that we can run each optimization pass more than once. For example, dead code elimination is often run many times due to its computational cheapness and the fact that dead code is often generated by other optimization passes. It could be worth exploring that as well.