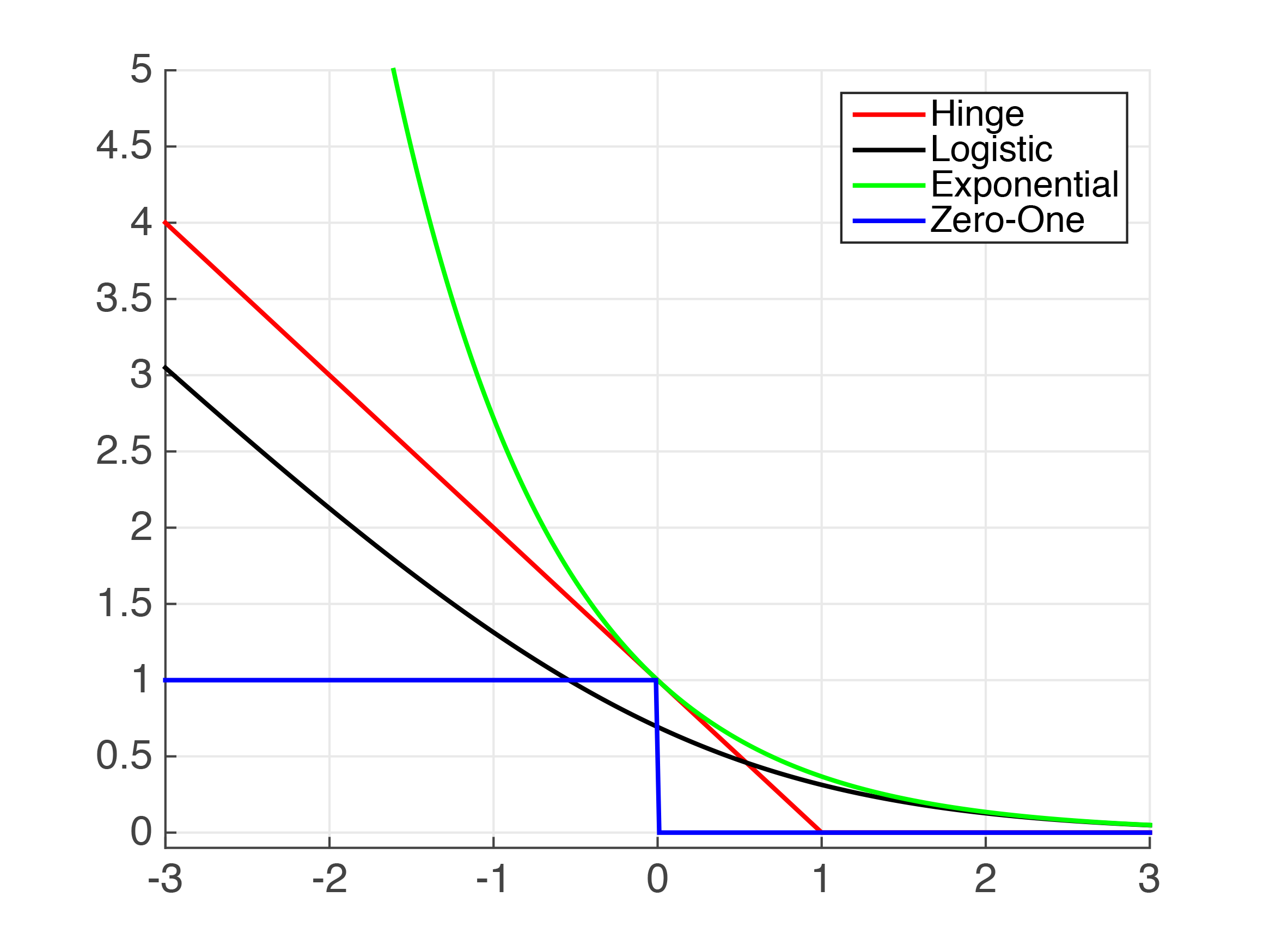
Figure 4.1: Plots of Common Classification Loss Functions - x-axis: \(\left.h(\mathbf{x}_{i})y_{i}\right.\), or "correctness" of prediction; y-axis: loss value
| Loss \(\ell(h_{\mathbf{w}}(\mathbf{x}_i,y_i))\) | Usage | Comments | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hinge-Loss\(\max\left[1-h_{\mathbf{w}}(\mathbf{x}_{i})y_{i},0\right]^{p}\) | When used for Standard SVM, the loss function denotes the size of the margin between linear separator and its closest points in either class. Only differentiable everywhere with \(\left.p=2\right.\). | ||||||||||||||||
| Log-Loss \(\left.\log(1+e^{-h_{\mathbf{w}}(\mathbf{x}_{i})y_{i}})\right.\) | Logistic Regression | One of the most popular loss functions in Machine Learning, since its outputs are well-calibrated probabilities. | |||||||||||||||
| Exponential Loss \(\left. e^{-h_{\mathbf{w}}(\mathbf{x}_{i})y_{i}}\right.\) | AdaBoost | This function is very aggressive. The loss of a mis-prediction increases exponentially with the value of \(-h_{\mathbf{w}}(\mathbf{x}_i)y_i\). This can lead to nice convergence results, for example in the case of Adaboost, but it can also cause problems with noisy data. | |||||||||||||||
| Zero-One Loss \(\left.\delta(\textrm{sign}(h_{\mathbf{w}}(\mathbf{x}_{i}))\neq y_{i})\right.\) | Actual Classification Loss | Non-continuous and thus impractical to optimize. |
Some questions about the loss functions:
Figure 4.1: Plots of Common Classification Loss Functions - x-axis: \(\left.h(\mathbf{x}_{i})y_{i}\right.\), or "correctness" of prediction; y-axis: loss value
| Loss \(\ell(h_{\mathbf{w}}(\mathbf{x}_i,y_i))\) | Comments | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
Squared Loss \(\left.(h(\mathbf{x}_{i})-y_{i})^{2}\right.\) |
|
||||||||||
|
Absolute Loss \(\left.|h(\mathbf{x}_{i})-y_{i}|\right.\) |
|
||||||||||
Huber Loss
|
|
||||||||||
|
Log-Cosh Loss \(\left.log(cosh(h(\mathbf{x}_{i})-y_{i}))\right.\), \(\left.cosh(x)=\frac{e^{x}+e^{-x}}{2}\right.\) |
|
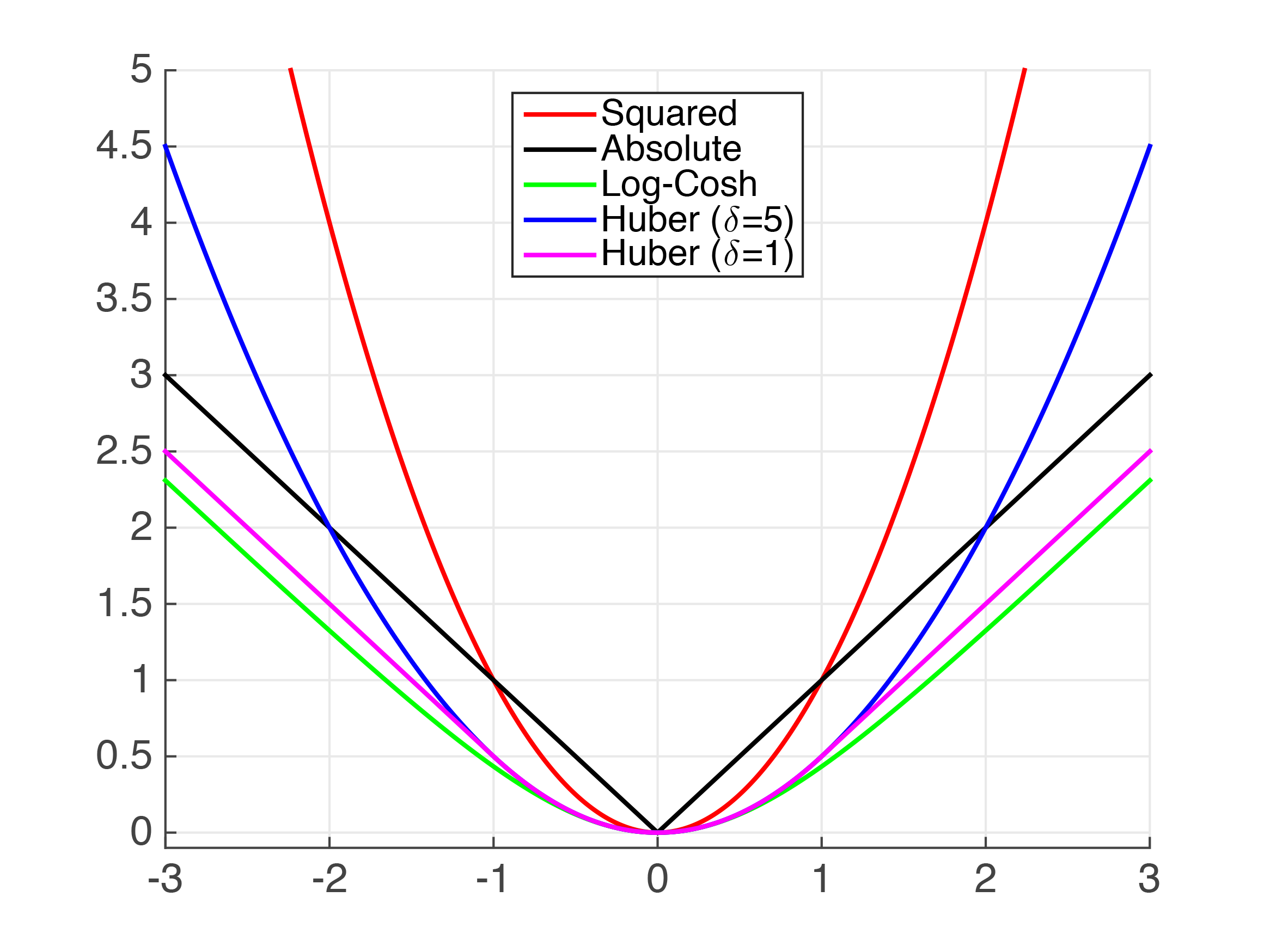
Figure 4.2: Plots of Common Regression Loss Functions - x-axis: \(\left.h(\mathbf{x}_{i})y_{i}\right.\), or "error" of prediction; y-axis: loss value
| Regularizer \(r(\mathbf{w})\) | Properties | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| \(l_{2}\)-Regularization \(\left.r(\mathbf{w}) = \mathbf{w}^{\top}\mathbf{w} = \|{\mathbf{w}}\|_{2}^{2}\right.\) |
|
||||||||||
| \(l_{1}\)-Regularization \(\left.r(\mathbf{w}) = |\mathbf{w}|_{1}\right.\) |
|
||||||||||
| \(l_p\)-Norm \(\left.\|{\mathbf{w}}\|_{p} = (\sum\limits_{i=1}^d |v_{i}|^{p})^{1/p}\right.\) |
|
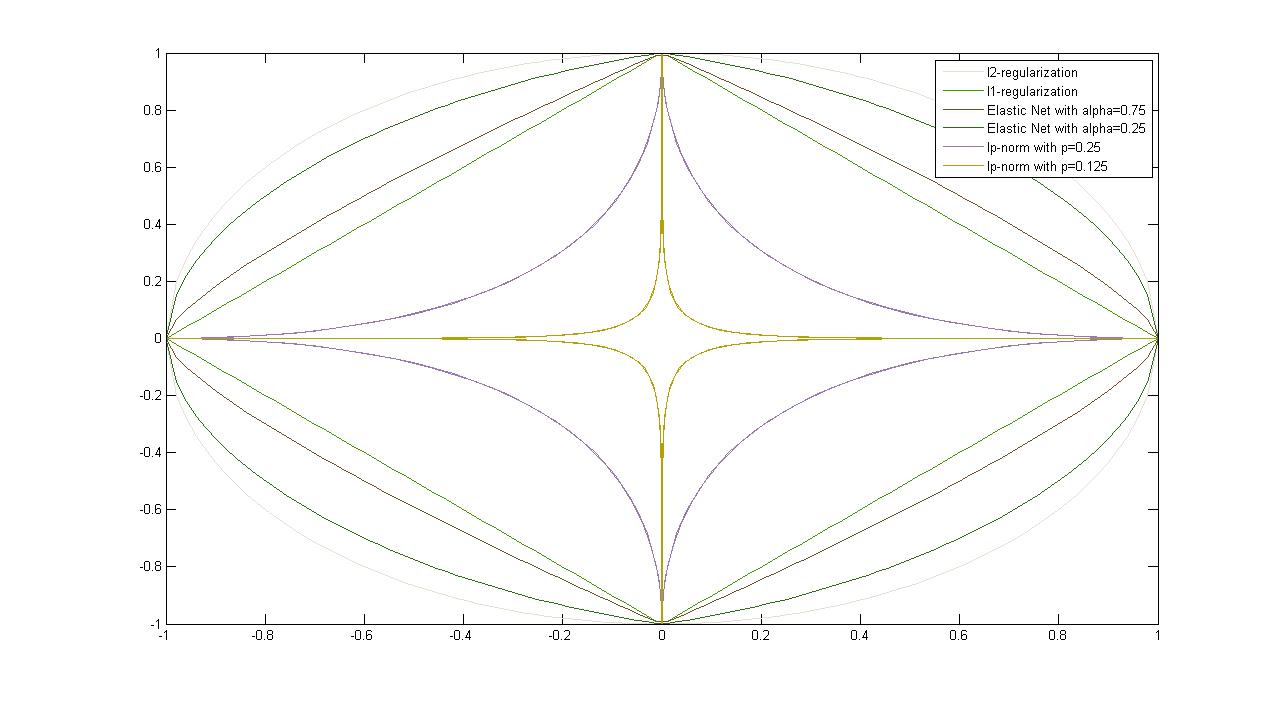
Figure 4.3: Plots of Common Regularizers
| Loss and Regularizer | Comments | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ordinary Least Squares \(\min_{\mathbf{w}} \frac{1}{n}\sum\limits_{i=1}^n (\mathbf{w}^{\top}x_{i}-y_{i})^{2}\) |
|
||||||||||
| Ridge Regression \(\min_{\mathbf{w},b} \frac{1}{n}\sum\limits_{i=1}^n (\mathbf{w}^{\top}x_{i}+b-y_{i})^{2}+\lambda\|\mathbf{w}\|_{2}^{2}\) |
|
||||||||||
| Lasso \(\min_{\mathbf{w},b} \frac{1}{n}\sum\limits_{i=1}^n (\mathbf{w}^{\top}\mathbf{x}_{i}+b-{y}_{i})^{2}+\lambda |\mathbf{w}|_{1}\) |
|
||||||||||
|
Elastic Net \(\min_{\mathbf{w},b} \frac{1}{n}\sum\limits_{i=1}^n (\mathbf{w}^{\top}\mathbf{x}_{i}+b-{y}_{i})^{2}\) \( +\left.\alpha |\mathbf{w} |_{1}+(1-\alpha)\|{\mathbf{w}}\|_{2}^{2}\right.\) \(\left.\alpha\in(0, 1)\right.\) |
|
||||||||||
| Logistic Regression \(\min_{\mathbf{w},b} \frac{1}{n}\sum\limits_{i=1}^n \log{(1+e^{-y_i(\mathbf{w}^{\top}\mathbf{x}_{i}+b)})}\) |
|
||||||||||
| Linear Support Vector Machine \(\min_{\mathbf{w},b} C\sum\limits_{i=1}^n \max[1-y_{i}(\mathbf{w}^\top{\mathbf{x}_i+b}), 0]\) \(+\|\mathbf{w}\|_2^2\) |
|
||||||||||