CS5625 PA5 Reflection Mapping

Due: Friday March 18, 2015 at 11:59pm

Work in groups of 2.

Overview

In this programming assignment, you will implement:

  1. a shading model for a perfect mirror material taking a cube map as the source of incoming light,
  2. a system for rendering the scene into a cube map so that it can be used with the shading model in the previous item,

Task 1: Reflective material from cube map

Edit:

so that they together implement a material that reflects an environment map, represented by a cube map, like a perfect mirror.

The ReflectionMaterial material class contains two important fields:

Let us first discuss how the reflective material works. Suppose, at the shaded point, we have a computed the direction the direction $\mathbf{r}_{\mathrm{cube}}$, which represents the direction that a perfect mirror should reflect the view direction from its surface. Then, the fragment color of the shaded point is simply given by:

gl_FragColor = textureCube(mat_cubeMap, $\mathbf{r}_{\mathrm{cube}}$);

How do we get $\mathbf{r}_{\mathrm{cube}}$? The fragment shader is given two varying variables geom_normal and geom_position, so we can compute a view direction and a normal vector from it. Since these uniforms are in camera space, the resulting vectors are also in camera space, which we shall denote by $\mathbf{v}_{\mathrm{cam}}$ and $\mathbf{n}_{\mathrm{cam}}$. From these vectors, we can compute the reflected direction $\mathbf{r}_{\mathrm{cam}}$, which is also in camera space. (As a note, you can use the GLSL built-in reflect function to compute $\mathrm{r}_{\mathrm{cube}}$, but BE VERY CAREFUL OF WHAT IT EXPECTS AS ARGUMENTS.) This is not exactly what we want because we want the vector in the cube map space.

To get the vector in cube map space, first realize that, if $\mathbf{r}_{\mathrm{world}}$ is the reflected direction in world space, then $$ \mathbf{r}_{\mathrm{cam}} = M_{\mathrm{view}} \mathbf{r}_{\mathrm{world}}. $$ In other words, $$ \mathbf{r}_{\mathrm{world}} = M_{\mathrm{view}}^{-1} \mathbf{r}_{\mathrm{cam}}. $$ Once we have the vectors in world space, we can use $M_{\mathrm{world}\rightarrow\mathrm{cube}}$ to transform them to the cube map space: \begin{align*} \mathbf{r}_{\mathrm{cube}} &= M_{\mathrm{world}\rightarrow\mathrm{cube}} \mathbf{r}_{\mathrm{world}} = M_{\mathrm{world}\rightarrow\mathrm{cube}} M_{\mathrm{view}}^{-1} \mathbf{r}_{\mathrm{cam}}. \end{align*}

Next, let us discuss the source of the cube map. The interface TextureCubeMapData represents an object that can fulfill the functionality. It is implemented by two classes for two different situations:

The process that derives an OpenGL cube map from these objects has already been implemented in the forward renderer, so you do not have to worry about it. Nevertheless, you are responsible for setting up the right transformations so that the cube map are looked up correctly.

A correct implementation of the cube map should produce the following appearance on the top sphere:

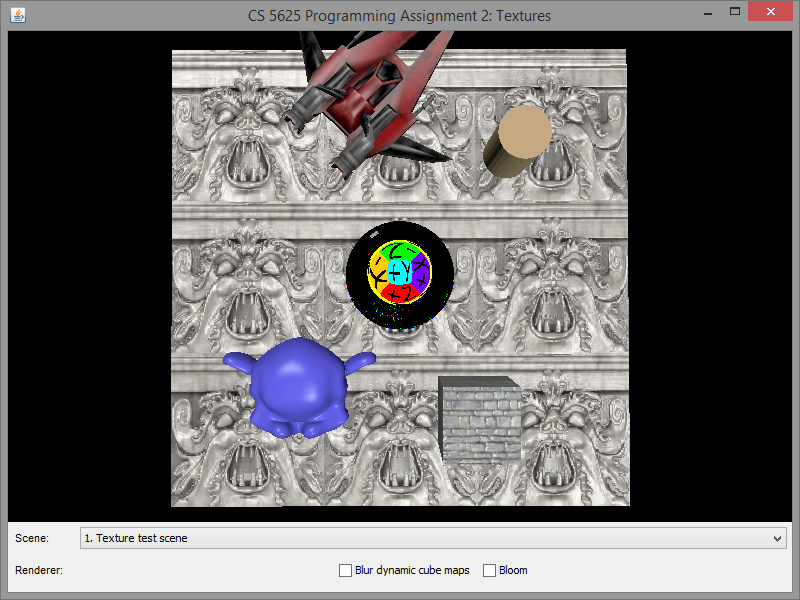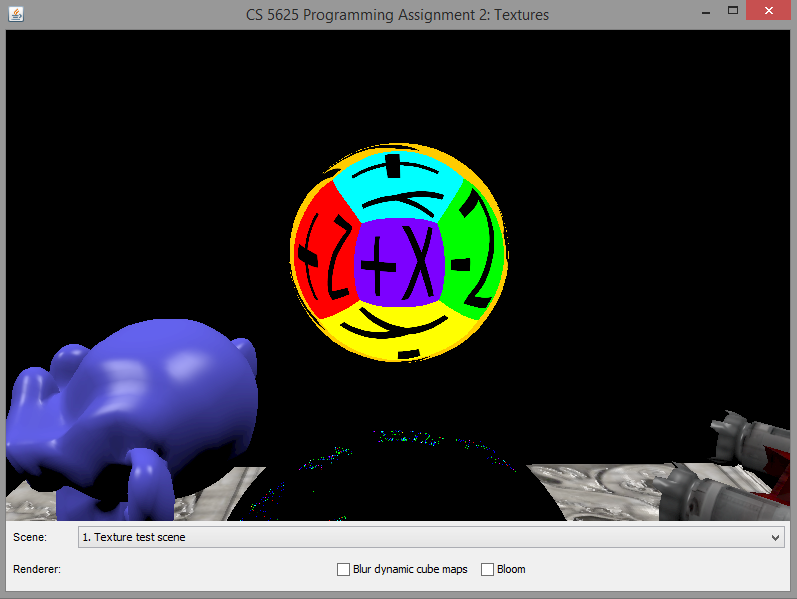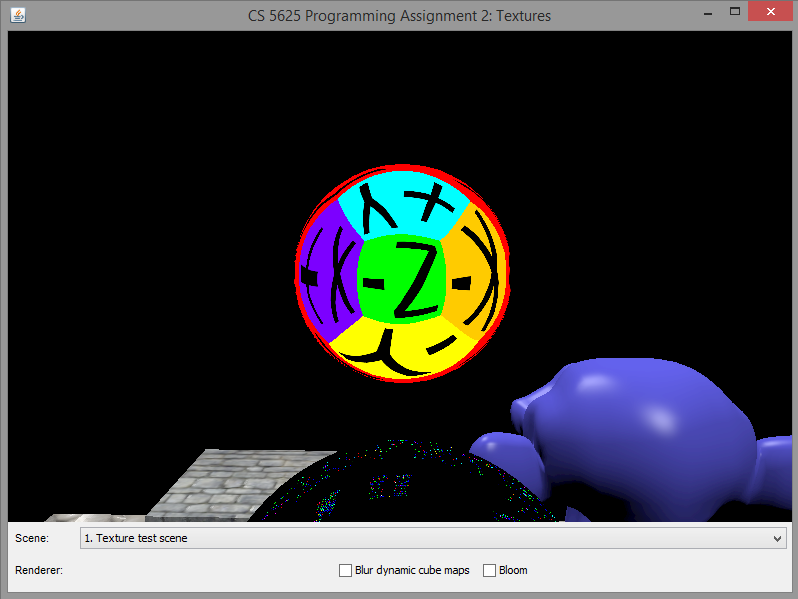Note that, since we have not implemented the dynamic cube map, the bottom sphere would display some random images depending on the contents of the GPU memory before the program ran. As such, the images displayed by your program might be different from what are shown in the example images above. This is not an issue, and you should proceed to the next task.

Task 2: Dynamic cube map

Edit:

so that it renders the scene and stores the results in cube maps that can be used as environment maps later.

How a cube map should be rendered is determined by the CubeMapProxy object, which represents an imaginary cube located in the scene. A CubeMapProxy has a name by which the RenderedTextureCubeMapData refers to it. It also has information on the resolution of the cube map and other rendering parameters.

The ForwardRenderer locates all the CubeMapProxy objects in the scene using the collectCubeMapProxies method. It stores the proxies in a HashMap called cubeMaps so that they can be indexed by name. For each proxy, it creates an auxiliary object of class CubeMapInfo that contains several objects useful for cube map rendering:

You will see that, in the code, the renderCubeMapProxies method iterates through all the proxies, and it allocates the cubeMapBuffers and textureRectBuffers for each of the proxy.

To render a cube map, you should iterate through its six sides. For each side, set up the camera so that:

  1. The camera is located at the center of the cube.
  2. It looks through the correct side of the cube.
  3. When setting up the perspective camera, set the near clip to the distance between the center and the side, and set the far clip to the farClip field of the CubeMapProxy object.
To do this, you will need to modify three fields of the ForwardRenderer: projectionMatrix, viewMatrix, and inverseViewMatrix. You might find that the makeProjectionMatrix and the makeLookAtMatrix methods in the VectorMathUtil class useful. Looking at the render method of the ForwardRenderer, you shall discover that you can render the whole scene to a texture rectangle by calling the renderSceneToTextureRectBufferAndSwap method. Also, the proxy resides in a scene tree node, so it has its own modeling transformation. You need to take into account this transformation when setting up the cameras.

Due to the filtering that we will be performing in the next section, we advise that you render to the textureRectBuffers first, then copy the resulting content to the appropriate side of cubeMapBuffers.

A correct implementation of the dynamic cube map rendering should produce the following images:

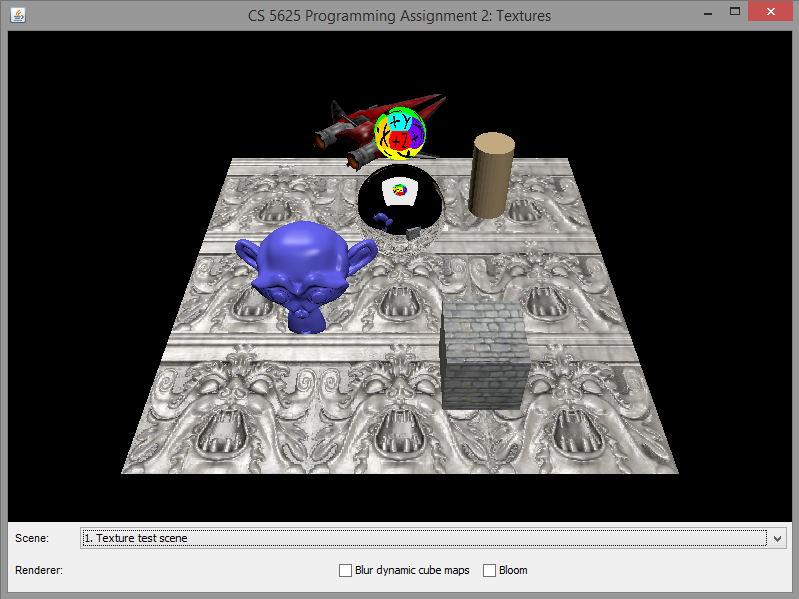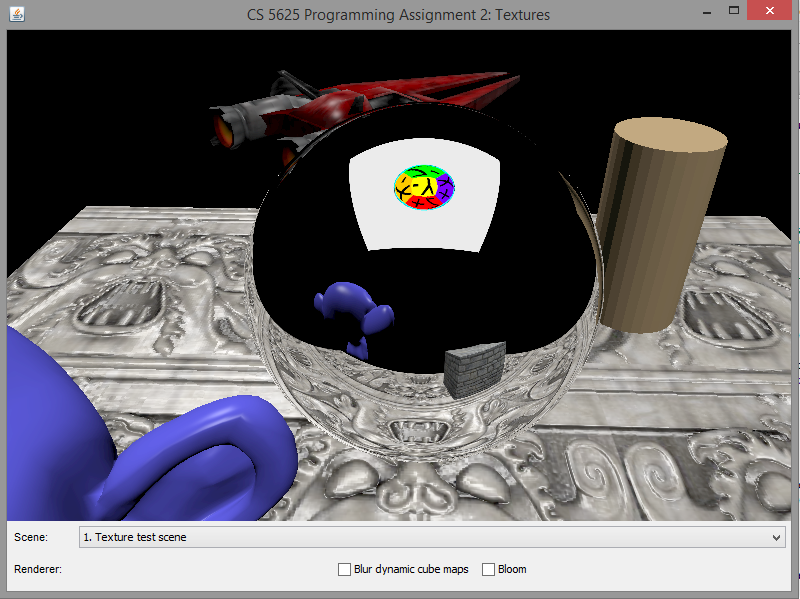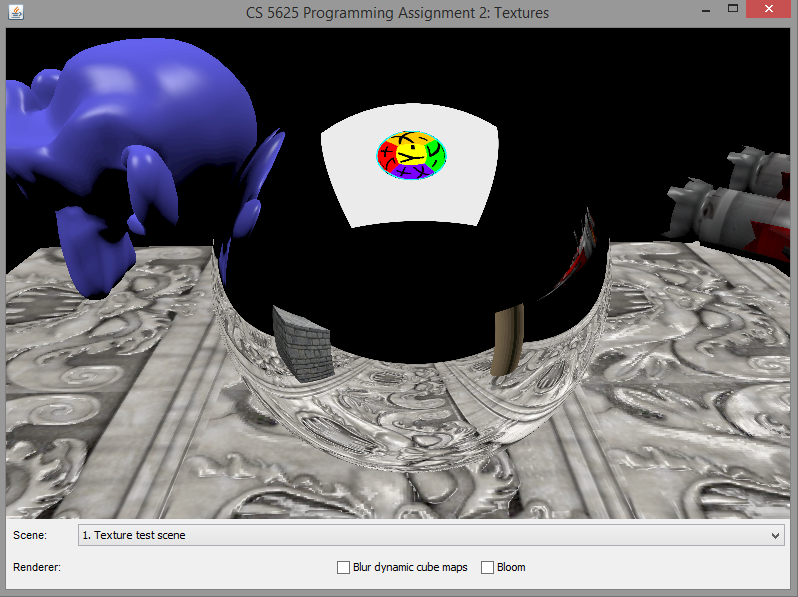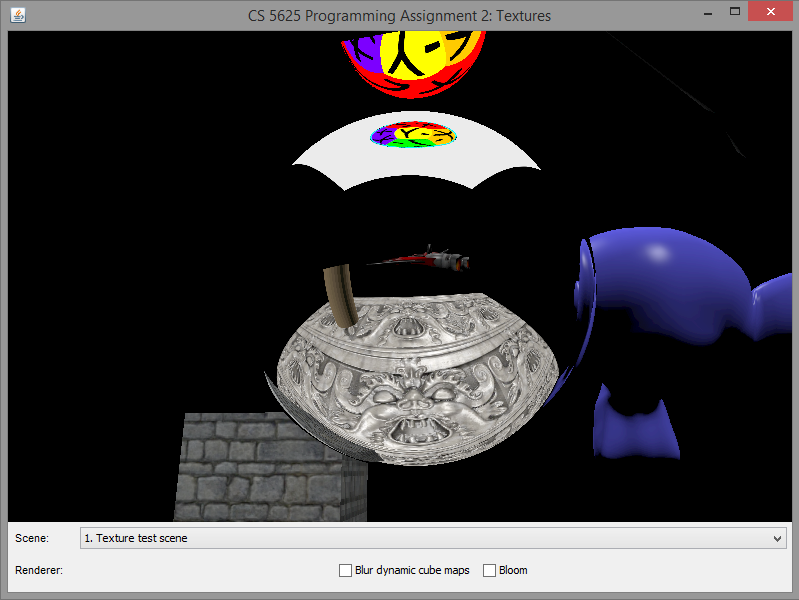Task 3: Cube map filtering

We have implemented a mechanism for dynamic cube map in the last task, which allows us to simulate a mirror-like object being embedded in the scene. One way to simulate roughness of the material's surface is to blur the cube map. In this way, the higher the blurring, the rougher the surface becomes.

Edit:

so that the renderer applies a Gaussian blur to the rendered cube map when blurring is enabled by the program.

In the last task, you should have rendered the scene to the textureRectBuffers before copying the resulting image to the appropriate cube map side. In this task, before copying the image to the cube map, you should run the Gaussian blur shader to the rendered image two times, one for the x-axis and another for the y-axis, if the dynamicCubeMapBlurringEnabled field is set to true.

The gaussian blur fragment shader should implement a 1D Gaussian blur. To get a 2D blur, you have to apply it two times. The shader contains the following uniforms that specify the Gaussian kernel:

You should set their values so that they agree with the specification in the CubeMapProxy object. That is, Lastly, axis should be set to 0 in one pass and 1 in another pass that you apply the shader.

A correct implementation should yield the following differences between the rendered images:

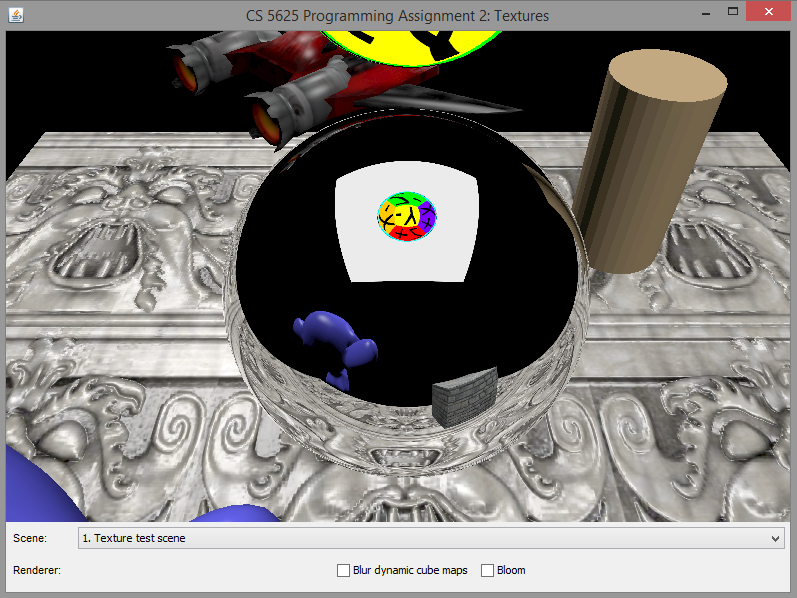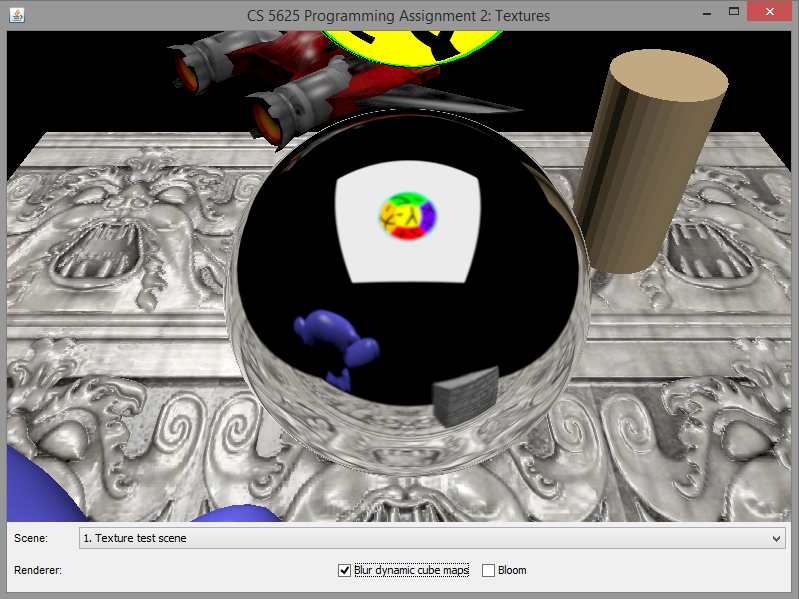No blurring With blurring