Theory of Protection Matricies

Lecturer: Professor Fred B. Schneider

Lecture notes by Lynette I. Millett

The state of a system with respect to access control can be represented by an access control (protection) matrix. Last lecture we defined a small programming language for defining commands and access control matrix in terms of subjects, objects, and rights. With commands we can specify how the protection matrix evolves during the execution of the system. In this discussion we assume that the sole purpose of a system is to change access privileges to objects, ignoring other computations that might be occurring.

There are three issues that we discuss today. The first is that of rights propagation. Can a given subject ever get access to a particular object? The second is enforcement: How can we ensure that any attempt to, for example, read an object is mediated by the protection matrix? Finally, we explore representations of access control matrices.

Rights Propagation

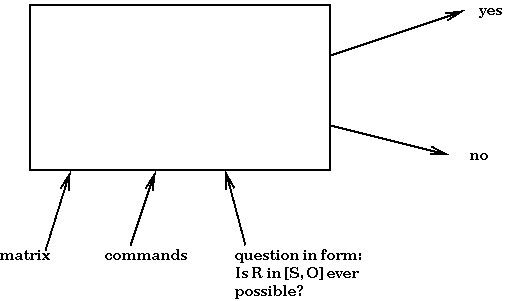
It would certainly be useful to have an analyzer that could answer the question: Is it possible for right r to be an element of [S, O] after some execution? Such an analyzer would provide a way to understand the ramifications of a given set of commands.

Recall, we have already demonstrated that we are using a very simple model of security and access control. However, even given this simplicity, it was proved in 1978 that the rights propagation question is undecidable. It is not possible to build the desired analyzer. Thus, complicating our model by perhaps making the programming language richer can only make the problem even more undecidable. A less complicated model might be decidable, but our current model is probably already too restrictive.

We now outline a proof of the undecidability result. In the proof, we show that a Turing Machine (TM) can be represented as a protection system. If we could build an analyzer as described above, then the analyzer could be used to determine whether a TM could halt. We know that the "Halting Problem" is undecidable, so have arrived at a contradiction. Thus, the analyzer cannot be built.

Briefly, a TM consists of an infinite tape and a control device with a read/write head and a finite-state control. The read/write head can move one square to the right or left and can read and write symbols onto the current tape square. We must show how to think of a TM as a protection problem. In other words, we encode a TM as a protection system where a particular right (r being an element of [S, O]) is equivalent to the TM halting. Once a TM is represented this way, then if a rights-propagation analyzer for a protection system exists, we would have a way to determine whether a TM halts.

The first step for the encoding is to create the protection matrix from the TM's tape. We encode the contents of the TM's tape on the diagonal of the protection matrix; element [S, S] will contain the Sth tape square. Recall also that subjects and objects aren't ordered, and thus any permutation of rows or columns is an equivalent protection system. We need some way to encode the fact that tape square S1 comes before tape square S2. This is down by making "own" a member of the element [Si, Si+1]. So, the matrix now looks something like:

We also need to encode the state of the TM. We say, for example, that rights Q and E are elements of [S5, S5] when the TM is in state Q, the read/write head is on square 5, and symbol E is in [S5, S5]. Changing the state of the TM is equivalent to commands that delete and add rights. Now, the question of whether a TM halts is equivalent to asking: Is QFinal an element of [S1, S1]? (NB: There are restrictions that make this problem decidable, for instance, restricting the number of commands, or only allowing one operation in each command.)