Lecture 2: k-nearest neighbors

The k-NN algorithm

Assumption: Similar Inputs have similar outputs
Classification rule: For a test input $x$, assign the most common label amongst its k most similar training inputs

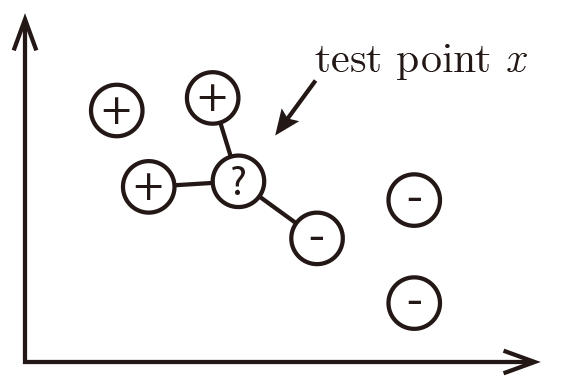
Neighbors' labels are $2\times$ ⊕ and $1\times$ ⊖ and the result is ⊕.


Formally:
  • Test point: $\mathbf{x}$
  • Define $S_\mathbf{x}\subseteq {D}$, s.t. $|S_\mathbf{x}|=k$ and $\forall(\mathbf{x}',y')\in D\backslash S_\mathbf{x}$, \[\text{dist}(\mathbf{x},\mathbf{x}')\ge\max_{(\mathbf{x}'',y'')\in S_\mathbf{x}} \text{dist}(\mathbf{x},\mathbf{x}''),\] and \[h(\mathbf{x})=\text{mode}(\{y'':(\mathbf{x}'',y'')\in S_\mathbf{x}\}),\] where $\text{mode}(\cdot)$ means to select the label of the highest occurrence.
    • (Hint: In case of a draw, a good solution is to return the result of $k$-NN with smaller $k$)

    What distance function should we use?

    Most common choices: Minkowski distance \[\text{dist}(\mathbf{x},\mathbf{z})=\left(\sum_{r=1}^d |x_r-z_r|^p\right)^{1/p}\]
  • $p = 1$: Manhattan Distance ($l_1$ norm)
  • $p = 2$: Euclidean Distance ($l_2$ norm)
  • $p \to 0$: (not well defined)
  • $p \to \infty$: Maximum Norm

    • Quiz2: How does $k$ affect the classifier. What happens if $k=n$? What if $k =1$?
  • $k = n$ => return the mode of the data set
  • $k = 1$ => very sensitive to distance
    • Cover and Hart 1967[1]: As $n \to \infty$, the $k$-NN error $\le2\times$ optimal
    Quick digression: What is the Bayes optimal classifier? Assume you knew $\mathrm{P}(y|\mathbf{x})$. What would you predict?
    Examples: $y\in\{0,1\}$ \[ \mathrm{P}(+1| x)=0.8\\ \mathrm{P}(-1| x)=0.2\\ \text{Best prediction: }y^* = h_\mathrm{opt} = argmax_y P(y|\mathbf{x})\] (You predict the most likely class.) What is your error? $1-\mathrm{P}(h_\mathrm{opt}(\mathbf{x})|y) = 1- \mathrm{P}(y^*|\mathbf{x})$ (In our example, that is 0.2.) You can never do better than the Bayes Optimal Classifier.

    Back to k-NN

    $n$ small

    $n$ large

    $n\to\infty$

    Let us focus on the case with $k=1$. Let $\mathbf{x}_\mathrm{NN}$ be the nearest neighbor of our test point $\mathbf{x}_\mathrm{t}$. As $n \to \infty$, $\text{dist}(\mathbf{x}_\mathrm{NN},\mathbf{x}) \to 0$, i.e. $\mathbf{x}_\mathrm{NN} \to \mathbf{x}_{t}$. (This means the nearest neighbor is identical to x.) You return the label of $\mathbf{x}_\mathrm{NN}$. What is the probability that this is not the label of $\mathbf{x}$? (This is the probability of drawing two different label of $\mathbf{x}$) \begin{multline*} \mathrm{P}(y^* | \mathbf{x}_{t})(1-\mathrm{P}(y^* | \mathbf{x}_{NN})) + \mathrm{P}(y^* | \mathbf{x}_{NN})(1-\mathrm{P}(y^* | \mathbf{x}_{t}))\\ \le (1-\mathrm{P}(y^* | \mathbf{x}_{NN})+(1-\mathrm{P}(y^* | \mathbf{x}_{t}) = 2(1-\mathrm{P}(y^* | \mathbf{x}_{t}) = 2\epsilon_\mathrm{BayesOpt}, \end{multline*} where the inequality follows from $\mathrm{P}(y^* | \mathbf{x}_{+})\le 1$ and $\mathrm{P}(y^* | \mathbf{x}_{NN})\le 1$.
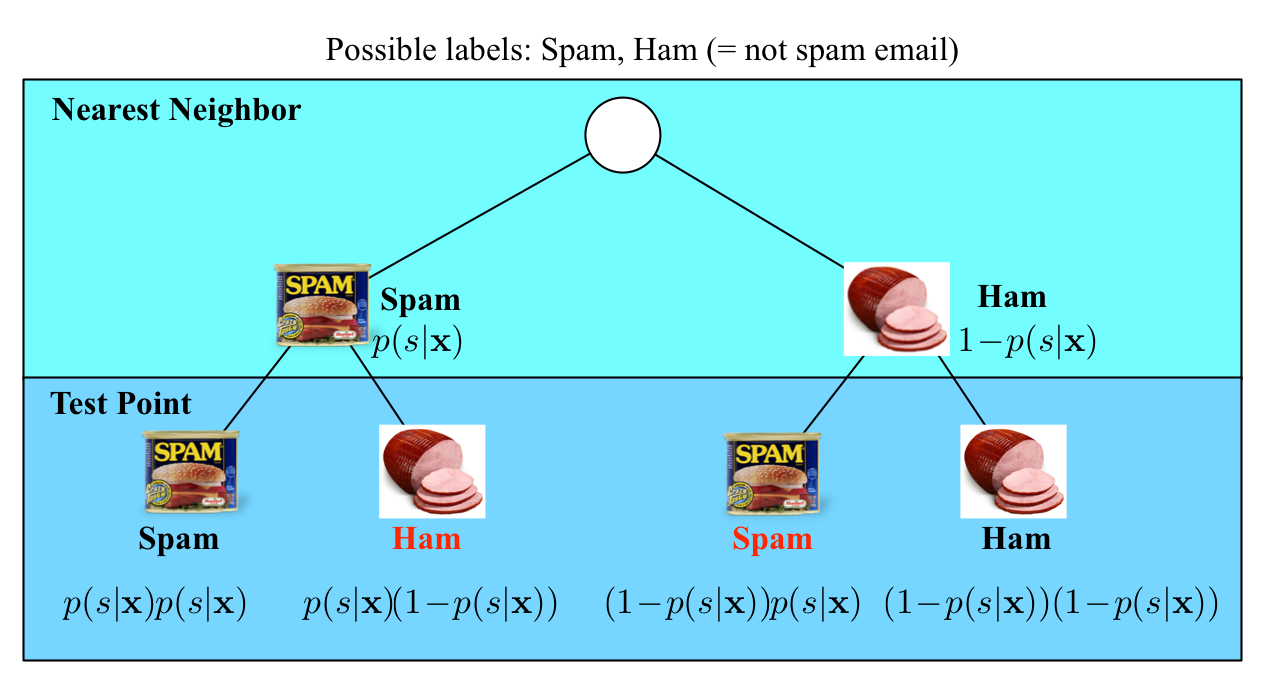    In the limit case, the test point and its nearest neighbor are identical. There are exactly two cases when a misclassification can occur: when the test point and its nearest neighbor have different labels. The probability of this happening is the probability of the two red events: $(1\!-\!p(s|\mathbf{x}))p(s|\mathbf{x})+p(s|\mathbf{x})(1\!-\!p(s|\mathbf{x}))=2p(s|\mathbf{x})(1-p(s|\mathbf{x}))$

    Good news: As $n \to\infty$, the $1$-NN classifier is only a factor 2 worse than the best possible classifier.
    Bad news: We are cursed!!

    Curse of Dimensionality

    Imagine $X=[0,1]^d$, and $k = 10$ and all training data is sampled \textit{uniformly} with $X$, i.e. $\forall i, x_i\in[0,1]^d$
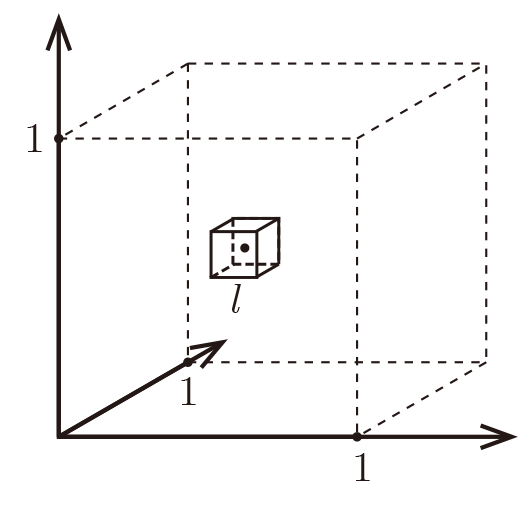
    Let $\ell$ be the edge length of the smallest hyper-cube that contains all $k$-nearest neighbor of a test point. Then $\ell^d\approx\frac{k}{n}$ and $\ell\approx\left(\frac{k}{n}\right)^{1/d}$. If $n= 1000$, how big is $\ell$?
    $d$$\ell$
    20.1
    100.63
    1000.955
    10000.9954
    Almost the entire space is needed to find the $10$-NN.

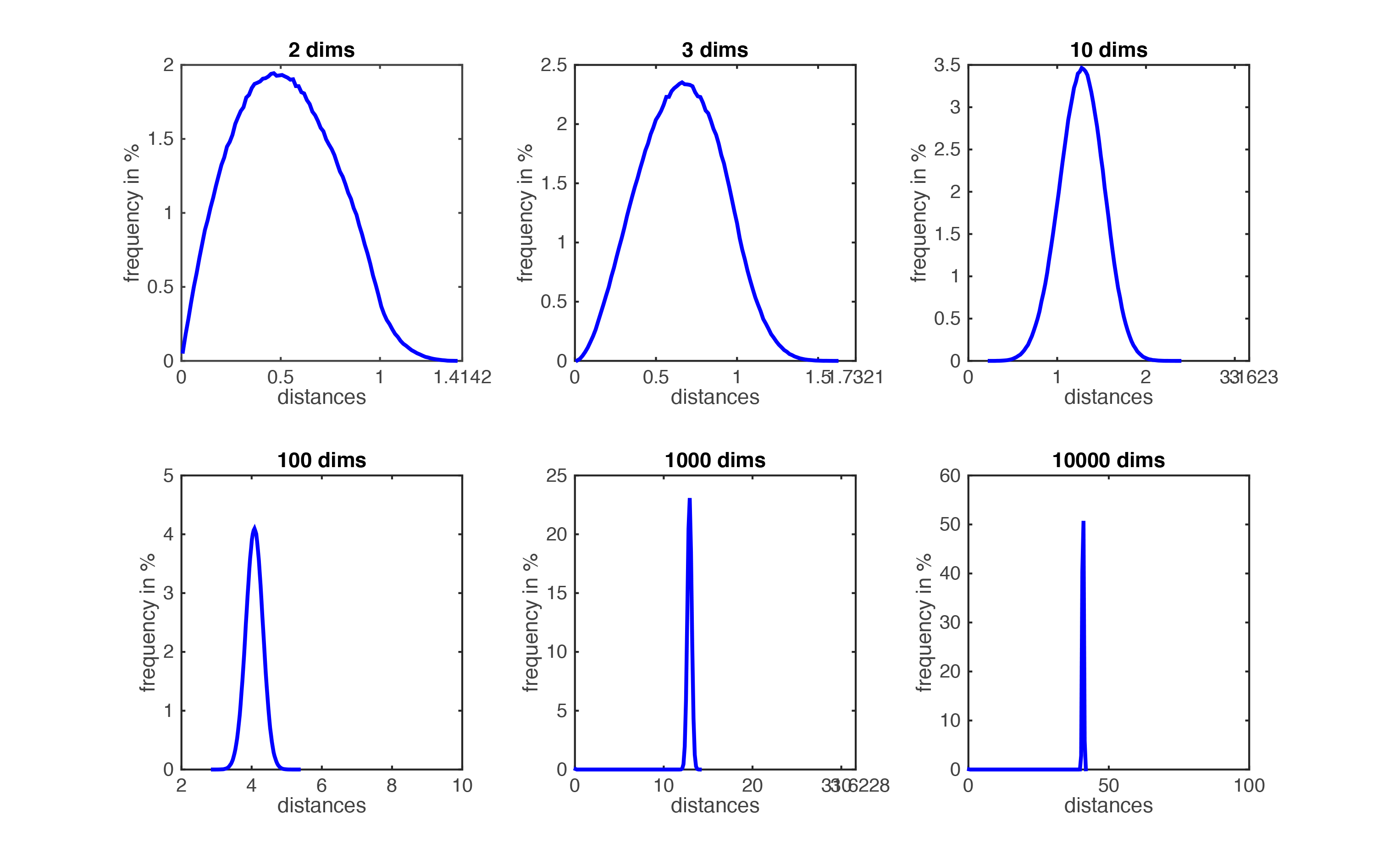
    Figure demonstrating ``the curse of dimensionality''. The histogram plots show the distributions of all pairwise distances between randomly distributed points within $d$-dimensional unit squares. As the number of dimensions $d$ grows, all distances concentrate within a very small range.

    Imagine we want $\ell$ to be small (i.e the nearest neighbor are \textit{truly} near by), then how many data point do we need? Fix $\ell=\frac{1}{10}=0.1$ $\Rightarrow$ $n=\frac{k}{\ell^d}=k\cdot 10^d$, which grows exponentially!
    Rescue to the curse: Data may lie in low dimensional subspace or on sub-manifolds. Example: natural images (digit, faces).

    k-NN summary

  • $k$-NN is a simple and effective classifier if distances reliably reflect a semantically meaningful notion of the dissimilarity. (It becomes truly competitive through metric learning)
  • As $n \to \infty$, $k$-NN becomes probably very accurate, but also very slow.
  • As $d \to \infty$, the curse of dimensionality becomes a concern.

    • Reference

    [1]Cover, Thomas, and, Hart, Peter. Nearest neighbor pattern classification[J]. Information Theory, IEEE Transactions on, 1967, 13(1): 21-27