hw6 assignment handout (v.3, Thu Dec 4 11:56) | framework code (v.3, Fri Dec 5 17:41)
support libraries: Win32 | MacOS X
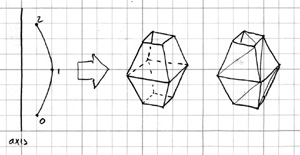
hw6-v3.pdf: fixed factual error in preparation question 3
and added illustration.
hw6-v2.pdf: added "preparation questions," several figures,
and additional explanation in many places; also updated to reflect changes
to framework.
hw6.pdf: initial release
spline-v3.zip: added modes to the MeshView window so that
you can see how you're doing even if something is not quite right. Changes
only affect MeshView.java.
spline-v2.zip: added the ability to delete junctions in the
spline; added sliders to control thresholds; added text readouts; changed
from enforcing C1 continuity to just G1. Changes only affect
SplineEditor.java and MeshView.java.
spline.zip: initial release
Cool demo: Take a look at these applets illustrating Bézier curves, by Jens Gravesen at TU Denmark. Particularly the one on de Casteljeau's algorithm is helpful for this assignment. [Thanks to Alvin Law.]
Q: The writeup says, "the spacing threshold is always 5
times the distance threshold." Does this mean I should multiply the threshold
by 5 when evaluating the spacing criterion?
A: No, it means that the threshold that the framework
supplies when illustrating the spacing criterion in the debug mode is 5 times
the number that it supplies when using the distance criterion (which is what
you adjust with the slider). As it turns out, the code to let the user split
a spline uses a fixed spacing of 3 pixels. (See lines 309 and 503 in
SplineEditor.java.)
Q: Why does the number in the readout from the left-hand
slider seem to be 100 times the number that shows up in
the tolerance parameter to BezierSpline.getPoints?
A: The GUI reports the threshold for the absolute distance
criterion in pixels to make the readout more understandable, but the numbers
passed to your code are measured in scene units. There happen to be exactly
100 pixels per scene unit (the window is 500 pixels wide, and you can see 5
big squares across it).
Q: I'm still not quite sure where to start with the surface
triangulation.
A: I'd suggest (using the latest version of MeshView) that
you first focus on getting the vertex positions right (looking just at the
points view), then focus on getting the triangles rigth (looking just at the
mesh view), then work on getting the normals right (looking at the surface
views). (Note that you'll have to put in some placeholder normals in order
for the triangle views not to throw exceptions -- just allocate the right size
array and set all the normals to (0,0,0).)
Here is an example. Suppose you set the flatness tolerance so coarse that your spline only has three points and your revolution only has four angles going around. Then your mesh would look like this:
If we unwrap the mesh into a flat grid of triangles, it's easier to see how they connect up:
In this example, supposing we number the vertices across, then up (so that
vertex (i,j) gets assigned index 4*i + j), then the triangles are:
(4, 0, 5), (1, 5, 0), (5, 1, 6), (2, 6, 1),
(6, 2, 7), (3, 7, 2), (7, 3, 4), (0, 4, 3),
(8, 4, 9), (5, 9, 4), (9, 5, 10), (6, 10, 5),
(10, 6, 11), (7, 11, 6), (11, 7, 8), (4, 8, 7).
In the IndexedTriangleMesh class, the
arrays positions and normals have length 12, and
triangles is an array of 16 arrays of length 3.
Q: There don't seem to be enough parameters to getPoints to
support the recursion. How do I figure out what level of subdivision I'm doing?
A: You probably want to define another version
of getPoints with extra arguments to keep track of at least the
recursion level, then call that from the existing getPoints.
Q: When I output the points for a segment, is it all four
control points?
A: No, just ouput the endpoints, because it is harder to come up with
tangents for the middle points. Your termination tests should be
comparing the whole spline segment to the line joining its endpoints.
Q: What should I do to get started?
A: The quickest way to get up and running is to (a)
implement divide and then (b) set up getPoints so
that it unconditionally subdivides 8 levels deep. This just requires a call
to divide and then two recursive calls (along with a test for
the maximum recursion depth). Fill in dummy values for ts to
get started, then figure out how to get the right ones (the segment-splitting
operation in the UI is the only thing that uses ts).
Q: At what stage should I begin to see the spline? I'm assuming after
implementing part of BezierSpline.getPoints?
A: You're already seeing the spline, in a sense—the
placeholder implementation of getPoints returns the control
points, so it just draws over the control polygon in black. Once you change
getPoints so that it returns something else, you'll see the
spline curve drawn in black and the control polygon overlaid in gray. Here
is a screenshot of the interface as it looks when you're done:
Q: Does the parameter criterion
that is passed into getPoints correspond to: 0 for absolute
distance, 1 for uniform spacing, and 2 for flat/relative distance? The
orders in which these are presented are different in the handout and in
the comments
A: Use the symbolic
constants BezierSegment.CRITERION_DISTANCE and friends.
Q: Do the elements of ts, points,
and tangents need to be in any particular order beyond the need
to have them be in the same order?
A: Yes, they need to be in order along the spline. The
spline will be drawn using a single polyline, so if the points are in some
other order you'll see the line zigzagging around.