CS412/413
Introduction to Compilers and Translators
Spring 1999

There were many misuses of regular expression syntax on this problem, including misuses of quotation marks, commas, the ^ symbol, and brackets. Please be sure you are comfortable with all of the regular expression metacharacters. These mistakes were already made in homework 1. The regular expression metacharacters are described in lecture 2.
 

1. Identifiers that must start with an alphabetic character and may continue with any number of alphabetic or numeric characters, or the character $, but may not contain two $'s in a row.


alpha ::= [A-Za-z]
alphanum ::= [A-Za-z0-9]+

identifier ::= alpha alphanum? ( $ alphanum ) * $? or
identifier ::= alpha $? ( alphanum $ ) * alphanum?

Expanding references, we get:

identifier ::= [A-Za-z] [A-Za-z0-9]* ( $ [A-Za-z0-9]+ ) * $? or
identifier ::= [A-Za-z] $? ( [A-Za-z0-9]+ $ ) * [A-Za-z0-9]*

Another possible solution was:

identifier ::= [A-Za-z] $? ( [A-Za-z0-9] $? ) *

The basic strategy in designing this regular expression was to allow a $ to be inserted in between any sequence of non-$ characters at any point in the string (except for the beginning).

Common mistakes: starting with a number, allowing $$, including commas inside of brackets, using question marks in strange places. Six testcases were used to break most of the broken grammars:
 

id	id$	id3$kj3$	id$kj3$
	id3	id$kj3$kj3	id3$kj3$kj3


 

2. Non-empty strings of lowercase alphabetic characters that are not the keyword if.


alpha ::= [a-z]
[a-eg-z] ::= [a-eg-z]
no_i ::= [a-hj-z]

string ::= alpha no_f | no_i alpha | alpha | alpha alpha alpha+ or
string ::= no_i alpha* | i | i no_f alpha* | i f alpha+

Expanding references, we get:

string ::= [a-z] [a-eg-z] | [a-hj-z] [a-z] | [a-z] | [a-z] [a-z] [a-z]+ or
string ::= [a-hj-z] [a-z]* | i | i [a-eg-z] [a-z]* | i f [a-z]+

Each of the possible solutions represented a slightly different strategy. In the first example, we simply note the fact that all one- and three-or-more-character strings are allowed, and then handle the two-character strings on a case-by-case basis (if the second letter is an `f', then the first character cannot be an `i', and if the first letter is an `i', then the second letter cannot be an `f'.

In the second example, we note the fact that all strings not beginning with an `i' are allowed, and then handle strings beginning with an `i' on a case-by-case basis (one-, two-, and three-or-more-character strings).

Common mistakes: allowing "if", not recognizing three-character strings, using [^if]+ (this means "strings containing any character except i or f"). Some test cases used to monkey with the grammars:
 

i	fi	iaf	iff
ifi	ia	fif


 

3. Non-empty strings containing the same number of a's and b's, and no other characters.


There is no such regular expression. All regular expressions may be represented as DFA's. A DFA must store information such as the difference between the number of a's and b's as a state. Each difference of 1 therefore requires a state. Since the difference between the numbers of a's and b's is unbounded, the number of states is unbounded. Since DFA's by definition have a finite number of states, it follows that there is no such DFA and therefore no such regular expression capable of representing such a string.

One point was deducted for not making explicitly clear the relationship between a regular expression and the states required in a DFA to represent that regular expression.
 

• The notation [ A ] denotes zero or one occurrences of the string of terminals or non-terminals A.
• The notation ( A ) denotes exactly one occurrence of A, and is used for grouping.
• The notation A* denotes zero or more occurrences of A.
• The notation A+ denotes one or more occurrences of A.
• The notation A  B denotes a sequence of alternating A's and B's that starts and terminates in A, e.g. A, ABA, ABABA, etc.

        function_call ::= id ( [ expr  , ] )

Each of these extra notations can be eliminated by rewriting the grammar. Show how to rewrite a grammar to eliminate uses of each of the following EBNF operators, without introducing ambiguity into the grammar.
 
 

1. The [] operator. Assume you have a production of the form A ::= a [ b ] c. Show an equivalent production or productions that will derive the same strings.


A ::= a A' c
A' ::= b | e
 

2. The * operator. Start with a production of the form A ::= a ( b ) * c


A ::= a A' c
A' ::= b A' | e
 

3. Similarly, show that the  operator can always be eliminated by rewriting the grammar.


Suppose we start with a production such as A ::= a ( b  c ) d

A ::= a b A' d
A' ::= c b A' | e
 

S ::= E $
E ::= while E do E
    | id := E
    | E + E
    | id
 

1. Draw enough of the LR(0) automaton for this grammar so that states corresponding to at least two of the shift-reduce conflicts are shown. Note that you do not need to draw the entire automaton; only enough of the states to show two different conflicts.


 
2. Write a program or programs in this language to illustrate each of the ambiguities you found in your answer to part (a).


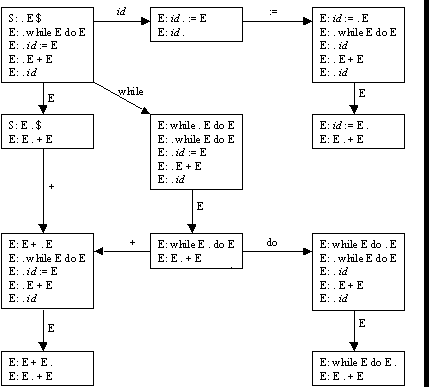
Some possible code fragments:

id1 := id2$
id1 + id2 + id3$
while x + y + z do x + y $
 

E ::= ( E E )
    | ( function id : T E )
    | ( if E E E )

An expression of the form ( E₁ E₂ ) means that expression E₁ is to be evaluated, returning a function value, which is applied to the result of evaluating E₂. A function expression defines a new function value with a single argument id whose type is T. The body of the function is the expression E. As in most programming languages, when a function expression is applied to an argument, the value of the expression is the value of the body of E with the argument value substituted for the occurrences of the argument variable (call-by-value semantics). An if expression evaluates its first argument and decides whether o to evalutae and return the second or third expression depending on whether the value was true or false, respectively. We also have certain pre-defined symbols: integer constants, the symbol +, which has the type int -> ( int -> int), and the constants true and false, with type bool.

For example, the expression ((+ 2) 3) has the value 5, since the expression (+ 2) returns a function that adds two to its argument. The expression (function x ((+ x) x)) returns twice the value of whatever argument it is given, since it adds the argument x to itself. Therefore, the value of the expression ((function x ((+ x) x)) 10) is 20.
 

1. What is the type of the expression (function x : int x)?


int -> int
 

2. What is the type of the expression

(function x : int (function y : int -> int (y x)))?

int -> ((int -> int) -> int)
 

3. Is the following expression well-typed; if not, why? if so, what is its type?

((if true (function a : int a) (function b : int 0)) 1)

int
 

4. Complete the static semantics for the typed lambda calculus. All three inference rules need to be completed in some way. You may rewrite the rules from scratch if you like, but the rules as given may be completed to produce a correct static semantics.

 

A |- E1 : T2 -> T3 A |- E2 : T2 A |- (E1 E2) : T3	A U { id : T } |- E : T1                     A |- (function id : T E) : T -> T1
A |- E1 : bool A |- E2 : T A |- E3 : T  A |- (if E1 E2 E3) : T