Homework 10 Solution
CS409 - Spring 1999
Due: Thursday, April 29
1. Show the execution of the Ford-Fulkerson algorithm on the following flow network.
See page 595 in the text for an example of how to show the execution of the
algorithm.
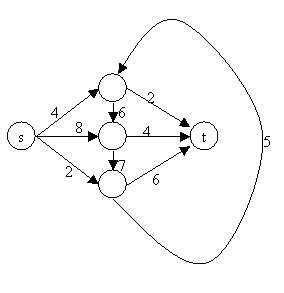
More than one solution is possible here. I'll use a, b, and c
for the top, middle and bottom vertices, respectively. For my first augmenting path,
I'll use s, b, c, t. This path allows 6 units of flow and results in the following
residual graph. It's hard to draw pictures here so I'll just list the edges in a
format that is (I hope) easily readable.
s4a a6b a2t
s2b b6s b1c c6b b4t
s2c c5a t6c
My next augmenting path is s, a, b, t which can carry 4 units of flow. Here's the
resulting residual graph.
a4s a2b b4a a2t
s2b b6s b1c c6b t4b
s2c c5a t6c
The next augmenting path is s, c, a, t which can carry 2 units of flow. Here's
the residual graph.
a4s a2b b4a t2a
s2b b6s b1c c6b t4b
c2s c3a a2c t6c
At this point there is no longer a way to get from s to t so the algorithm is done,
producing a total flow value of 12.
2. [from Ahuja, Magnati, Orlin 1993]
- Dating Problem. A dating service receives data from p men and p women. These
data dtermine what pairs of men and women are mutually compatible. Since the dating
service's commission is proportional to the number of dates it arranges, it would like to
determine the maximum number of compatible couples that can be formed. Explain how
to formulate this problem as a matching problem. (Note that each man or women is
assigned at most one date.)
Create a vrtex for each man and a vertex for each woman. Draw an edge between
each pair of vertices that correspond to a potential compatible couple. Finding the
maximum number of compatible couples corresponds to finding the maximum matching in this
bipartite graph.
- Seat Sharing Problem. Several families are planning a shared car trip on scenic
drives in the White Mountains, New Hampshire. To minimize the possibility of any
quarrels, they want to assign individuals to cars so that no two members of a family are
in the same car. Explain how to formulate this problem as a network flow problem.
Create a source s, a sink t, a vertex for each family and a vertex for each car.
Each unit of flow corresponds to a person. Connect the source to each of the
family vertices with an edge of capacity equal to the family size; this places the right
number of members in each family. Connect each car-vertex to the sink with an edge
of capacity equal to the car's number of passengers; this ensures that each car can carry
the right number of people. Connect each family vertex to every car vertex with an
edge of capacity 1; this ensures that no more than one member of each family goes into any
one car. It's easy to see the correspondence between a satisfying assignment of
people to cars and the max-flow in the graph.
- Ignore this problem (it doesn't reduce to MaxFlow; instead it
reduces to Bipartite Weighted Matching or to MinCostFlow, but we haven't talked about
these problems). Large-Scale Personnel Assignment. A recurring problem in the
US armed forces is efficient distribution and utilization of skilled personnel. Each
month thousands of individuals in the US military vacate jobs, and thousands of personnel
become available for assignment. Each job has particular characteristics and skill
requirements, while each person from the pool of available personnel has specific skills
and preferences. Suppose that we use this information to compute the utility (or
desirability) dij of each possible assignment of a person to a job. The
decision problem is to assign personnel to the vacancies in a way that maximizes the total
utility of all the assignments. Explain how to formulate this problem as a network
flow problem.

