Project 1: Solution

Below is the TA's implementation for project 1. The implementation is by no means the only correct one: several other approaches are equally valid. However, the given implementation is fairly efficient: in particular, the clustering algorithm presented below runs more efficiently than the recursive clustering procedure implemented by many students in the class. Here are the Matlab files:
alignCoords.m
Align amino acid coordinates according to sequence alignment
getDistance.m
Compute the minimum distance between two protein structures
clusterProteins.m
Perform clustering of proteins based on pairwise distances
project1.m
Matlab script to put it all together, and run the project
While there are several correct implementations, the right end results are unique. You can view the matrix of pairwise distances here, and the resulting clustering output here.

Grader's Comments

Below is the list of the most common errors made by students throughout project 1. Some errors prevented the code from working correctly, while others made it simply too inefficient.
  1. When computing the distance matrix, you don't use the fact that the distance between A and B is the same as the distance between B and A. You compute the distance between proteins i and j, and then again compute the distance between j and i. While this is a good way to test your distance computation routines, it is inefficient, since you are doing the same work twice. Therefore, this should be left out from the final version of your code.
  2. For every pair of proteins i and j, you call the pickAtom() function. This is very inefficient, since pickAtom() takes a long time to return (it must open a file, read from it, and perform complicated string processing). As the result, your program takes long to run, spending most of its time on pickAtom() calls. Furthermore, multiple calls to pickAtom() are redundant: it suffices to call the function only once for each protein, and store the returned coordinate matrix in a cell array. This would make your code run several times faster. See project1.m in the solutions for an example of how this is done.
  3. There is a mistake in the way you align amino acid coordinates based on sequence alignment. There were several types of errors here, but most common kind was not updating indices into the coordinate matrices correctly when gaps were encountered in either aligned sequence. See alignCoords.m for an implementation of coordinate alignment.
  4. In computing the rotation matrix U, you did not take into account the case where det(U) is -1.
  5. In computing the minimum distance, when handling the case that the determinant of the rotation matrix U is -1, you negate the smallest eigenvalue. However, in doing so, you neglect the case that one of the eigenvalues might be 0. Such an eigenvalue will be the smallest, but negating it will not accomplish anything. Rather, you must find the smallest positive eigenvalue, and negate it.
  6. There is a mistake in your clustering algorithm. Rather than use the recursive formula given on the website to compute the distance between two compound clusters, you directly retrieve all the leaf clusters contained in the nested compound clusters, and compute the average of all the pairwise distances between these leaf clusters. While this method produces the correct output in the case of this assignment, it does not follow the definition of cluster distance as specified in the project. Nor is it a valid alternative for defining cluster distances, since it fails to take into account the nested structure of each cluster. Consider, for instance, the following example:

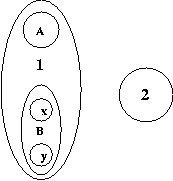
    Here, clusters labeled A, x, y, and 2 are leaves, and clusters labeled 1 and B are compound. Let D(1,2) denote the distance between 1 and 2. Then, according to the project definition, 

       D(1,2) = (D(A,2) + D(B,2))/2 = (D(A,2) + [D(x,2) + D(y,2)]/2) / 2 = D(A,2)/2 + D(x,2)/4 + D(y,2)/4
    whereas, according to your implementation, 
       D(1,2) = D(A,2)/3 + D(x,2)/3 + D(y,2)/3
    The above two expressions are clearly different, and latter is incorrect, since it does not in any way acknowledge the fact that A is a leaf cluster, and x and y are clustered together.