CS 321

Exact sequence comparison.

Sequence alignment is a tool to test for similarities between a sequence of an unknown target protein, and a single (or a family of) well-characterized protein(s). It is assumed that sequence similarity implies similarity in function.

Figure 1: A cartoon plot illustrating the use of a database of annotated proteins to identify a novel sequence

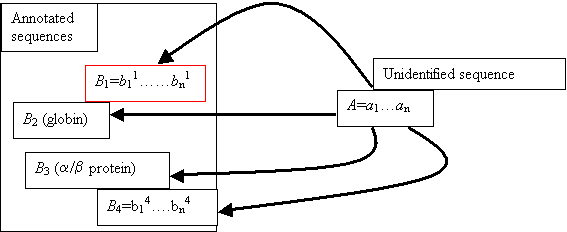
We denote the sequence of the unknown protein by . It is a short cut for an abbreviation of the explicit sequence , where is an amino acid placed at the position along the sequence. The sequences of the known proteins, that make the comparison database, are called where , and is the total number of proteins in the database. For sequences only, the database may include hundreds of thousands of entries [http://www.expasy.ch/srs5/]. Databases that include both sequences and structures are limited to about ten thousand entries [http://www.rcsb.org/pdb/]. For brevity we omit the index from and use to represent a member of the comparison set.

Table 1: A sample of protein sequences. Typical lengths of protein sequences vary from a few tens to a few hundreds. The single letter notation (one character for an amino acid) is used.

Serine Protease inhibitor

EDICSLPPEV GPCRAGFLKF AYYSELNKCK LFTYGGCQGN ENNFETLQAC XQA

Amicyanin alpha

MRALAFAAALAAFSATAALAAGALEAVQEAPAGSTEVKIAKMKFQTPEVR IKAGSAVTWTNTEALPHNVHFKSGPGVEKDVEGPMLRSNQTYSVKFNAPG TYDYICTPHPFMKGKVVVE

Major Histocompatability Complex (class I)

MAVMAPRTLV LLLSGALALT QTWAGSHSMR YFSTSVSRPG RGEPRFIAVG YVDDTQFVRF

DSDAASQRME PRAPWIEQEG PEYWDRNTRN VKAHSQTDRV DLGTLRGYYN QSEDGSHTIQ

RMYGCDVGSD GRFLRGYQQD AYDGKDYIAL NEDLRSWTAA DMAAEITKRK WEAAHFAEQL

RAYLEGTCVE WLRRHLENGK ETLQRTDAPK THMTHHAVSD HEAILRCWAL SFYPAEITLT

WQRDGEDQTQ DTELVETRPA GDGTFQKWAA VVVPSGQEQR YTCHVQHEGL PEPLTLRWEP

SSQPTIPIVG IIAGLVLFGA VIAGAVVAAV RWRRKSSDRK GGSYSQAASS DSAQGSDVSL

TACKV

b.2 An introduction definition ofto the alignment score

We need a more precise definition of similarA more precise definition of similar is needed. The simplest definition (one) is the fraction of amino acids in that are identical to . In proteins, high sequence identity (roughly above 35 percent) immediately implies close relationship. A more subtle definition of similarity (two) uses amino acids with similar physical or biochemical properties. For example, replacing a hydrophobic amino acid like leucine (L) by valine (V) is (usually) an acceptable mutation. The effect on the hydrophobic core of the protein is expected to be small. However, changing (L) to a charged residue like arginine (R) is likely to be damaging and significantly affect protein stability.

Hence, there is a gray area between an exact matching (two identical amino acids) and a complete mismatch. This gray area is better described by a scoring function with a wide spectrum. The scoring function gives the highest score to an identical pair and the lowest possible score for (to) substitutions that do not make chemical, physical or biological sense.

To make sequence comparison compact and easily extendable to a wide range of sequences, we simplify the process. We assume that the total score of comparing sequences and will be given by a sum of terms, each term comparing two elements, an element from and an element from . An element is either an amino acid or a “space” (gap). For example, consider the case in which is significantly longer than . In that (this) case it is obvious that some amino acids of will be aligned against “spaces” (gaps). The choice of the pairs of elements for the similarity test is called an alignment and is the focus of the present section.

Table 2. An example of an alignment of the two sequences and the selection of pairs of elements for comparison. The sequences of myoglobin and hemoglobin are placed on top of each other and pairs are compared horizontally.

PLACE TABLE 2 HERE

There are two different problems that we need to address: The selection of the alignment and the determination of the scoring function. Let us start with the score. Since we simplified the calculation of the total score, making it a sum of element comparisons, we need to consider only comparison of individual amino acids and comparisons of an amino acid against a gap. However, we do not need to consider separately scores of pairs of amino acids since .

The scores of pairs of amino acids, which measure the similarity of the -s and the -s, form the so-called substitution matrix . The matrix is symmetric, and of size (the number of amino acid types). Note that the term “substitution” may be misleading since it suggests a direction (substituting by implies that was there first). A symmetric matrix does not have a sense of time, and the order of substitutions does not change the score, or the degree of similarity.

Nevertheless, a non-symmetric variation of the sequence as a function of time is of considerable interest. A direction in sequence-similarity-scores is potentially informative, providing molecular fingerprints for evolutionary time scales. However, it is hard to estimate it without a specific model in mind. At present, for the purpose of finding protein relatives, we shall use the simplest way out and ignore the time arrow of evolution. A widely used (symmetric) substitution matrix is given below

The BLOSUM 50 matrix [x]

	A	R	N	D	C	Q	E	G	H	I	L	K	M	F	P	S	T	W	Y	V
:A	5	-2	-1	-2	-1	-1	-1	0	-2	-1	-2	-1	-1	-3	-1	1	0	-3	-2	0	:A
:R	-2	7	-1	-2	-4	1	0	-3	0	-4	-3	3	-2	-3	-3	-1	-1	-3	-1	-3	:R
:N	-1	-1	7	2	-2	0	0	0	1	-3	-4	0	-2	-4	-2	1	0	-4	-2	-3	:N
:D	-2	-2	2	8	-4	0	2	-1	-1	-4	-4	-1	-4	-5	-1	0	-1	-5	-3	-4	:D
:C	-1	-4	-2	-4	13	-3	-3	-3	-3	-2	-2	-3	-2	-2	-4	-1	-1	-5	-3	-1	:C
:Q	-1	1	0	0	-3	7	2	-2	1	-3	-2	2	0	-4	-1	0	-1	-1	-1	-3	:Q
:E	-1	0	0	2	-3	2	6	-3	0	-4	-3	1	-2	-3	-1	-1	-1	-3	-2	-3	:E
:G	0	-3	0	-1	-3	-2	-3	8	-2	-4	-4	-2	-3	-4	-2	0	-2	-3	-3	-4	:G
:H	-2	0	1	-1	-3	1	0	-2	10	-4	-3	0	-1	-1	-2	-1	-2	-3	2	-4	:H
:I	-1	-4	-3	-4	-2	-3	-4	-4	-4	5	2	-3	2	0	-3	-3	-1	-3	-1	4	:I
:L	-2	-3	-4	-4	-2	-2	-3	-4	-3	2	5	-3	3	1	-4	-3	-1	-2	-1	1	:L
:K	-1	3	0	-1	-3	2	1	-2	0	-3	-3	6	-2	-4	-1	0	-1	-3	-2	-3	:K
:M	-1	-2	-2	-4	-2	0	-2	-3	-1	2	3	-2	7	0	-3	-2	-1	-1	0	1	:M
:F	-3	-3	-4	-5	-2	-4	-3	-4	-1	0	1	-4	0	8	-4	-3	-2	1	4	-1	:F
:P	-1	-3	-2	-1	-4	-1	-1	-2	-2	-3	-4	-1	-3	-4	10	-1	-1	-4	-3	-3	:P
:S	1	-1	1	0	-1	0	-1	0	-1	-3	-3	0	-2	-3	-1	5	2	-4	-2	-2	:S
:T	0	-1	0	-1	-1	-1	-1	-2	-2	-1	-1	-1	-1	-2	-1	2	5	-3	-2	0	:T
:W	-3	-3	-4	-5	-5	-1	-3	-3	-3	-3	-2	-3	-1	1	-4	-4	-3	15	2	-3	:W
:Y	-2	-1	-2	-3	-3	-1	-2	-3	2	-1	-1	-2	0	4	-3	-2	-2	2	8	-1	:Y
:V	0	-3	-3	-4	-1	-3	-3	-4	-4	4	1	-3	1	-1	-3	-2	0	-3	-1	5	:V
*	* A	R	N	D	C	Q	E	G	H	I	L	K	M	F	P	S	T	W	Y	V	*

Note the high scores for a substitution of an amino acid to self (the diagonal elements of the matrix). Note also that certain amino acids have higher tendency for self-preservation (e.g. Cysteine) while a small and polar amino acid like threonine can be substituted to other amino acids more easily.

sequence alignment: definitions

Of course, theThe choice of pairs of amino acidselements (amino acids or gaps) from and is not completely free. The order of the amino acids in the sequence (the primary “structure” of the protein) counts, and our comparison should maintain that order. This is a significant restriction on the comparisons that we may make and limits our choices considerably. We are seeking the alignment of the two sequences that will give us the optimal (highest) score. Adding further to the complexity of the problem is the observation that not all proteins are of the same length; we need to account forpay attention to the variation in the lengths of the proteins and for the fact that some amino acids will not have corresponding amino acids to match. Two closely related proteins may be different at a specific site in which an amino acid was added to one protein but not to the second. To describe such cases we introduce a “gap” residue. A gap residue is denoted by “-“ and is used to indicate an empty space along the sequence. For example, the comparison of two proteins below (PDB codes 1rsy and 1a25_A, the “_A” denotes the first chain in the data entry) yields the following optimal arrangement of the two sequences with gaps:

TABLE: Optimal alignment of two sequences (top is 1rsy, Synaptotagmin I (First C2 Domain) , lower 1a25, Protein Kinase C (); Chain: A). The percentage of sequence identity is 33 percent.

EKLGKLQYSLDYDFQNNQLLVGIIQ-AAEL-PALDMGGTSDPYVKVFLLPD-K-KKKFE

ERRGRIYIQAHID-R--EVLIVVVRDAKNLVP-MDPNGLSDPYVKLKLIPDPKSESKQK

TKVHRKTLNPVFNEQFTFKVPYSELGGKTLVMAVYDFDRFSKHDIIGEFKVPMNTVD-F

TKTIKCSLNPEWNETFRFQLKESDKD-RRLSVEIWDWDLTSRNDFMGSLSFGISELQKA

GHVTEEWRDLQS

G-V-DGWFKLLS

A gap is placed in one sequence (say ) to match an amino acid in the second sequence (say ). It indicates a missing amino acid in the sequence when comparing it to the sequence. Note that it is not possible for us to decide if an amino acid was deleted from or added to , without a detailed evolutionary mechanism linking the two proteins to a common ancestor. At the level of alignment of a pair of sequences the two mechanisms are equivalent. It is therefore common to use the term indel to describe a gap (indel = an INsertion or a DELetion), a name that remains undecided about the mechanism of gap formation.

Our goal is to find the best match between two sequences including the possibilities of gaps. A score of a match is given (as argued above) by a sum of scores of matching elements. In order to score a given alignment and decide if it is good or bad we need a score for an indel.

What is the score of the gap, i.e. the alignment of an indel against another amino acid? It is philosophically useful to think ofn a gap as an ordinary amino acid and ask what is the score for substituting an amino acid type “” with an amino acid type “”. Such an approach is good in theory and there are some studies following this line of investigation. Unfortunately so far, determining gap scores (also called gap penalties) is still an open question. Formulation of statistical theories of gaps is difficult since the number of gaps in aligned sequences is not known to begin with. This difficulty in determining scores for gaps is in contrast with to the substitution matrices of amino acids that are pretty well established.

A common practice in alignment programs is to leave the gap energy as a parameter to be determined by the user, setting a default value of (for example) zero. This is not to say that the score of the gap is insignificant. The score of a gapIt clearly influences the alignment. If it is set too lowhighly negative, then it is difficult to match related proteins of considerable variation in lengths (remote homologous proteins). If it is set too high, two vastly different proteins may get fragmented to many small overlapping pieces and a large number of gaps. The fragmented alignment of two unrelated proteins (with high score for gaps scoring) may still maintain a good overall score. This is not what we expect, since We expect that proteins are related only if a substantial continuous fraction of the two sequences is similarfound to be similar.

High-scoring short-sequence segments can be analyzed statistically to determine their significance. In fact such an analysis is behind the popular BLAST algorithm [x]. To the first order BLAST does not consider gaps at all. A statistical test determines if short compatible segments of aligned sequences are significant. In some sense, BLAST solves the gap problem by avoiding it all together. The BLAST algorithm will be discussed in the section: Approximate alignments.

A typical practical solution estimate for of the indel/gap penalty is to give it a single negative value, say , regardless of the pairing amino. Hence, tThe gap penalty is set to be independent of the type of the amino acid it is aligned to (e.g. the pair score the same as the pair ). This choice is non intuitive since (tryptophan) is much larger than (glycine). The space left for the “-“ residue by the removal of or will be therefore different and the cost is likely to be dissimilar. The less detailed treatment of gaps, (compared to usual amino acids), can may lead to poor alignments. Therefore a few suggestions of extending the simple model of gap penalty were proposed.

One popular model is to differentiate between opening and extension of gaps. It is based on the argument that gaps should aggregate together. Claims were made that insertions and deletions are likely to appear at certain structural domains of proteins (mostly loops). The concentration of gaps at a few structural sites makes the indels appear together, and aggregate. To maximize the size of groups of gap (and minimize the number of gap clusters), two gap penalties are assigned:. One penalty is for initiating a gap group. A second (lower penalty) is for growing an existing gap cluster of gaps. For example, (we construct our alignment from left to right), extending an alignment from to is less favorable than the extension of the pair to . This is regardless of the fact that in both cases the same pair was added to an existing alignment.

This model improves the overall appearance of the alignments. However, the present author is not enthusiastic about it. It This model is highly asymmetric with respect to other “amino acids” (remember, we would like to consider a gap to be an amino acid), and it is not obvious that the asymmetry is indeed required. It is also making the identification of optimal alignment messier. Alternative modeling of gaps (so far less popular) will be discussed later and include structural dependent gap. For the moment we shall concentrate on the simplest model of gaps (one value does it all), and after solving that problem, the effect of the extensions will be examined.

We wish to place the gaps in such a way that the alignment or the comparison of the two sequences will be “optimal”, that is that the two sequences will be as similar to each other as possible. Early studies of sequence comparisons found optimal alignments manually. Gaps were inserted “by hand” into positions that made biochemical sense and increased the number of good-looking pairs [x]. For an implementation on the computer we consider an optimal alignment to be an arrangement of the two sequences with respect to each other in such a way that the total score of the alignment is as high as possible.

Let us examine in more details the problem of optimal alignments and possible arrangements of sequences. There are many ways of aligning a sequence against a sequence once gaps are introduced (even if the original order of the amino acids is maintained). Gaps can enter anywhere and in wide range of numbers in the alignment, creating many alternative arrangements. We denote the extended sequences of and (with gaps) as and . For example, might be . The introduction of the extended sequences raises another intriguing question, what is the maximum length of the sequences (or )?

Of course, the lengths may vary, but they still have upper bounds. Consider two sequences and of the same length -- . The maximum length of and should be . In the alignment of the extended-sequences that are also maximally long, every amino acid of or is aligned against a gap -- and . An increase of the length beyond the limit will necessarily include an alignment of an indel with respect to another indel, i.e. . Such an alignment does not make sense from a scientific point of view. We have no way to determine the number of “double gaps” or their locations. Moreover, also from a technical view point there is a problem if the pair generates a favorable plausible score. Consider the alignment

Let the total score be . Extending the above alignment by one more pair of indels, we have

The new score is where is the element of the substitution matrix replacing an indel by an indel. If the new score is better than , it is trivial to construct even a better alignment (and score) by adding yet another pair of indels with yet a better score of . The favorable extension with indels can proceed to infinite and is unbound. We therefore eliminate in our sequence-to-sequence alignments the possibility of . Note however, that if we wish to compare more than two sequences simultaneously (multiple sequence alignment), then the possibility of matching a gap against a gap exists. For example, two gaps may appear in the element comparison when matching three sequences.

Ok. It is settled then, the maximum length of is . How many possible alignments (with gaps) do we have? In a naïve approach, this number may be related to the number of scores we need to compute before deciding on the optimal alignment. Or how many we need to examine before deciding on an optimal alignment?

1.2 Counting alignments

To count the number of possible alignments, and as a starting point of the discussion on optimal alignments, we consider the dynamic matrix. The dynamic matrix is a table used for the alignment of two sequences. Below we provide one example for two sequences with the same length (). The rows are associated with the sequence and the columns with the . The numbers at different matrix entries will be explained below.

The hairy picture with the numerous arrows is actually telling. Paths in this table, which start at the upper left corner and end at the right lower corner, present all the possible alignments of the whole two sequences. From each entry in the dynamic matrix, there are three alternative moves: following Going down along the diagonal, going straight down, or moving to the right. A step in the matrix, which is a part of a legitimate alignment, never proceeds from to the left to right or up. For example, the thick line in the above matrix corresponds to the alignment:

A move along a diagonal aligns an amino acid against another amino acid. A vertical step in the matrix aligns a “” amino acid against an indel and a horizontal step puts a gap against an “” amino acid. Note that we use “” for the gap “residue” (or an indel).

The numbers at the different entries of the table denote the number of paths (alignments) that can reach this point. For example, there are 5 possible alignments of against (check the table element at the cross between and ). They are:

The last three alignments are essentially the sameinclude the same elements for comparison and are their scores are therefore degenerate. It is therefore not possible to decide on a “best” alignment from the group of three. There is more than one optimal alignment. At present, we consider all paths, including the degenerate pathsones. In the Appendix a clever counting protocol (by Dr. Jaroslaw Meller) is outlined that estimates the number of non-degenerate paths. Interestingly, the exact number of non-degenerate paths is . It has the same asymptotic behavior as the approximate lower-bound expression we sketched below for the number of all paths.

Another interesting property of this table is a summation rule and the possibility of constructing a recursion formula for the number of alignments. There are three ways (“sources”) to extend a shorter alignment to obtain one of the five longer alignments listed above. (a) Extend an earlier alignment by the pair , a diagonal move in the above table. Alternatively, (b) the pairs , or (c) (horizontal or perpendicular moves in the above table) can be used to extend a shorter alignment and to obtain a member of the above group.

Each of the three “sources” has its owna corresponding position in the matrix. The number at the entry to the matrix is the with a corresponding number of alignmentspaths aligning a segment of A against a segment of B. For example, before adding the pair we were at a table entry aligning against . We find that there is only one-way of aligning against a gap and “1” is indeed the corresponding entry.

Another example of extending the alignment is to add a gap against , which means that our earlier position in the table was the alignment of and . The last alignment can be done in three different ways and therefore the table entry is “3” ().

If we add the number of paths starting at the previous three “sources”, and leading to the number of alignments of with respect to we obtainsummed up to , exactly the number of alignments of our target.

To summarize the above empirical observations more precisely:

The number of possible alignments of -s against -s is defined as , this number can be determined using the recursive formula , and the initial conditions . Note that the definition of was done for computational convenience and it does not imply that “nothing” against “nothing” can be aligned in exactly one way.

While this formula can be used directly, it is useful to have a quick,n order-of-magnitude estimate of the number of alignments. This estimate is especially useful if we are planning a computation that will enumerate all of the alignments. If a calculation is not feasible with existing computer resources it is better knowing that it is not feasible in advance, and not after a few weeks of futile attempts to execute the desired computation.

A simple lower bound for can be obtained quickly. is a positive number, so we can write (we “forgot” for convenience the term in the original equality). So, the alternative recursion formula (with the same initial conditions as for ) always yields lower numbers than . For we have a close expression: . This formula is easy to verify by direct substitution of the closed expression to the recursion. Note that this I stheis the same as the (exact) results derived by Meller for non-degenerate paths (Appendix).

We now make use of the Stirling formula: [x], valid for large -s.

The logarithm of the number of alignments is estimated as

And the lower bound for the number of alignments is . For a short protein (; ) the number is substantial. and is beyond what we can do today in a systematic search. Even if the computation of a single alignment requires a nanosecond ( second), which is unrealistically fast, it still necessary to use to examine all possible alignments.

If this is not impressive enough, remember that this is a lower bound and the precise counting of all paths will yield a number significantly larger than this one. For example, for we have already a number significantly lower than the exact number in the table (1683). Hence, this estimate underlines the statement claim that it is impossible to examine all alignments one by one in order to find the alignment with the highest score.

Readers with a background in structural biology may recall the Levinthal paradox in protein folding. The paradox puts in contrasts the huge number of plausible protein conformations and the efficiency in which proteins fold in nature. We cannot be sure (until the next section) that there is a solution for the sequence alignment problem. However, nature solves the protein folding problem. So at least the existence of the solution for the protein folding problem is confirmed. This is (again) in contrast to sequence alignment for which an efficient solution exists.However, as As we see below a large space to search does not necessarily mean that optimization in that space is difficult. It is not obvious that the optimization must be performed at a cost proportional to the volume of that space. In fact it can be profoundly cheaper.

1.3 Dynamic programming and optimal alignments

After this long detour, it is about the time to return to the basic question: What is the optimal alignment of and ? The score matrix and the gap penalty are provided and we need is to fish out the alignment(s) with the highest overall score(s). This is a point in which algorithms developed by computer scientists can be extremely useful. The fact that the number of possible alignments is exponentially large in the sequence length does not mean that the search for the optimal alignment needs to be done in exponential time. Sequence alignments can be done with dynamic programming, an algorithm that requires only order of operations to find the alignment with the best score, a remarkable saving compared to operations- the number of all possible alignments.

The efficient search for the optimal alignments consists of two steps. In the first step a dynamic matrix is constructed (with different entries than what we have seen before) is constructed and in the second step an optimal path is found in the newly constructed table just constructed. The first step is similar to the counting of possible alignments and the recursive expression we wrote use to compute the total number of alignments. We denote the optimal score of the alignment of a sequence length against a sequence with length by , and consider the following question:

Assuming that a very kind fellow gave us the optimal scores for the following alignment: , , , can we construct the score ?

The answer is yes(!). Since the total score is given by a sum of the scores of the individual aligned pairs, we construct the score from the three alignments leading to it. We consider three possibilities to obtain an alignment of against amino acids.

Option a: Align against amino acids (this alignment has the known optimal score of ). Extend it by the alignment of with a score of which is the substitution score according to the types of the amino acids at and (e.g., the BLOSUM matrix). Hence the first suggestion for an optimal score is .

Option b: Align amino acids against amino acids. This alignment also has a known score, which is . Extend this alignment by with a corresponding score for a gap. The second possibility for an optimal alignment is therefore .

Option c: Align amino acids against amino acids with the known (optimal) score of . Extend the alignment, by adding with a corresponding score of . The third suggestion is therefore .

Note that we use the simple model of gaps in which only a single score is associated with an indel, regardless of the amino acid it is aligned against.

Our final task is to select the highest score from one of the three alternatives:

, , , which is the optimal score of .

More compactly, we write: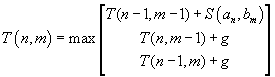

The above recursion can be used to fill with optimal scores the complete dynamic matrix. We start with the condition and use the initial values to grow the matrix. For example,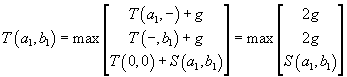

Where denotes alignment of nothing that (not surprisingly) scores zero. Another simple example is of . Hence, there is only one alignment against “all gaps” arrangement, providing us with immediate optimal scores for the first row and column of the dynamic matrix. It is also clear that similarly to the direct counting of the number of paths we can also construct all the optimal scores.

A simple pseudo code to create the dynamic matrix is given below

/* fill the first (zero) column and the first (zero) row */

T(0,0) = 0

Do I=1:n

T(I,0) = I*g

End do

Do I=1:m

T(0,I) = I*g

End do

/* Now fill the rest of the matrix picking the maximum value

from the three possibilities */

Do I = 1:n

Do J = 1:m

T(I,J) = max[ T(I-1,J)+g,

T(I,J-1)+g,

T(I-1,J-1)+S(a(i),b(j))]

End do

End do

Actually, if we are primarily interested in the score of the alignment of with respect to only a single element of the dynamic matrix, , is of interest. Of course, in order to get at it we need to compute first the whole matrix. However this score, which is recorded at the lower right side of the dynamic matrix, is only part of the story.

Besides the score, in many cases, it is important to know the alignment itself. The path in the dynamic matrix that corresponds to the optimal alignment can be found by a trace-back procedure. Starting from we ask “which of the three possible steps could have generated the final optimal score? That is, we examine the three possibilities

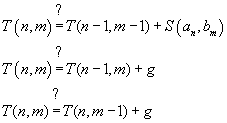
For at least one of the tests above the equality will hold. It is possible that more than one test is correct and in that case the optimal alignment is degenerate. Hence, there is more than one alignment that provides an optimal score. Usually we consider only one path. For example, if the first test is correct the alignment ends with the pair: and we repeat the three tests to find the next path segment, this time starting from . The process is repeated until it reaches the upper left corner and provides the desired optimal alignment. The maximum number of times that the process is repeated is (all the steps are horizontal or vertical) and the smallest number of steps is either or , the larger number of the two.

We are also ready for a rough estimate of the computational effort. As we discussed earlier a lower bound on the number of possible alignments is . Examining all possible alignments will require computational effort that is growing exponentially with . The computations that we just described, using dynamics programming, are much cheaper. Let us consider the two steps separately. In the first step we create the dynamic matrix . To generate a single element we need (about) four operations: Evaluating three expressions, and a decision which of the three is the largest. The calculation of a single element is therefore independent of or , and the cost associated with the computation of the matrix is proportional to (the number of matrix elements). To trace the path of alignment (once the matrix is known) takes a maximum of operations.