CS 321
Overlapping set of points
We consider two set of points: 
and 
that describes
two three-dimensional objects (e.g., 
of protein
chains). The (square of the) distance between the two coordinate sets is
defined by
(1)
where 
are the
Cartesian position of one point (
coordinates).
We did not write 
but 
to indicate that
there is a complication. Each of the protein chains remains unchanged upon
rigid body translations and rotations. For example, if I will increase each of
the 
by 5 the second
protein will still look exactly the same. More precisely, any transformation
that maintains the same distances between the points that make the object is a
rigid body transformation.
- There is an exception to this case. What is it?
It is easy to verify that the displacement of all the 
by 5 did not
alter any of the distances. Consider the original 
, it does not change by adding five to 
and 
. That is, 
. The conclusion is therefore that translations (three
translations along the x, y, and z axes) are legitimate rigid body
transformations. Similarly we can show that rotations do not change distances.
Consider a position vector 
. A rotation is performed by a applying a matrix 
on the vector 
. 
satisfies 
and 
. A distance between two points of the second object can be
written as:
If we apply the same rotation for every single vector representing point, the distance does not change:
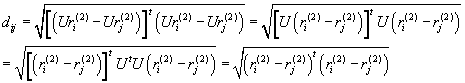
Translations and rotations do not affect the internal distances between internal points of a single object. However, if these operations apply to one object the distance between the two objects (equation (1)) depends on these operations. We need to make the definition of the distance unique. We therefore define the distance as the minimum value obtained by selecting optimal translations and the rotations.
For simplicity we consider separately the translations and the rotations. However, the separation does not affect the generality of our results.
Let us optimize the translation. We add to the points of the
first object a displacement vector 
. We have
We wish to determine 
so that 
is a minimum.
Differentiating 
with respect to 
we obtain
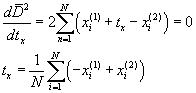
A similar argument follows for 
and 
.
Ok, that was easy. How about rotations? Rotations are a
little trickier; we will discuss them in steps. Let us first write the formula
for the distance in an adjusted form. We assume that the translations were
already taken care of (by fixing the geometric centers of the two proteins to
the (0,0,0)) coordinate) and apply the rotation for all points in the first
object. We also have to make sure that the matrix is unitary 
and for that
purpose we add Lagrange multipliers. We have (in an explicit form)
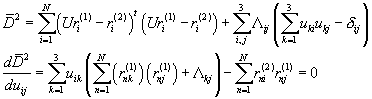
Consider the 3x3 matrices:
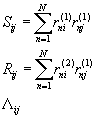
The minimum condition is written in a matrix notation as 
. Note that it is not so simple to solve the matrix e1quation
directly since we do not know 
and 
. In fact in many cases we can skip Alternatively multiplying the above equation by its
transpose, we have: 
. The matrix 
is symmetric but
is not.
Let 
be the
eigenvectors of 
. They are also the right eigenvectors of 
. Let 
bet the left
eigenvector of 
, 
is also the
product of applying 
on 
(
).
The eigenvalues of the symmetric matrix 
are 
.
Substituting in the expression for 
we have
Clearly the first summation over the squares of the vectors
from the first and second objects is independent of the rotations. Note also
that in writing the expression in the second line we used the unitary property
of the rotation matrix (otherwise 
). The rotation
matrix plays a role only in the last sum. Let 
and 
be the left and
right unit vectors that form an orthonormal basis for the matrix 
. That is 
or 
. We have now
for the last sum
Suggest now an algorithm to compute the minimal distance.
Suggest a procedure to determine the rotation matrix.
Are we done, or are there more problems to fix?