CS 221 -- Some properties of
rotations:
Let the rotation matrix be U. U is a 3x3 matrix that transforms a vector (rank 3) into another vector of rank 3 (say Ua = b ). U is special since it preserves the distance between any two vectors, i.e. ||a1 - a2|| = ||Ua1 - Ua2|| = ||b1 - b2|| with no inversion. Alternatively we may require that U tU = I and det(U) = 1.
Every 3D rotation can be
described as 2D rotations with three angles. Another option is to use a
rotation around a single axis (to be determined). Two angles determines the
direction of the axis and the last angle is a rotation around that axis
- Given a matrix U how to
determine the rotation axis?
A vector along the rotation
axis – eR will not be affected by applying U on it. Hence we have UeR =
eR. The rotation axis is
an eigenvector of U with
eigenvalue 1.
Here is a simple MATLAB
example:
Type in -
% find rotation axis
u = [0 1 0 ; -1 0 0 ; 0 0 1]
[v,d] = eig(u);
v
d
output
u =
0
1 0
-1
0 0
0
0 1
v =
0.7071 0.7071 0
0 + 0.7071i 0 - 0.7071i
0
0 0
1.0000
d =
0 + 1.0000i 0
0
0
0 - 1.0000i 0
0 0
1.0000
Our prime problem here is the
determination of U such that the
distance between two protein shapes will be minimal. Each of the Ca
-s in a protein has a three-dimensional vector (
rn - components x, y, and z) that determines its location in space. The distance (square) between two proteins
with the same number of amino acids is:
![]()
with the constraints U
tU = I and det(U)
= 1.
Here we shall not produce a
detailed proof of the final result (if interested in a proof check W. Kabsch,
Acta Crys. A32,922-923(1976) and A34,8270838(1978)) but will give the final
results and “qualitative rationale”.
We wish to find U that
minimizes D. To do that we
differentiate D with respect to
one of the U elements, say uij and set the result to zero.
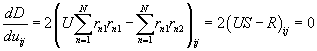
Is the solution U =
RS-1? NO! This solution does not satisfy (in
general) the conditions for a rotation matrix. So this is a place in which we
are not precise. It is necessary to build the constraints into the optimization
problem.
Note that R is an asymmetric matrix while S is a
symmetric matrix. Because R is
asymmetric, it has left and right eigenvectors. That is we have
![]()
where mi is the eigenvalue and ai and ai are the right and left eigenvectors respectively.
Note that for this matrix equation the sign of the eigenvalue cannot be
determined uniquely.
Consider the product R
tR: it is a symmetric matrix. Since U
tU = I, the product is equal S tS. Assuming
that the matrix is not degenerate, the eigenvector of S is the same as of S t (S is
symmetric); then the eigenvector of S is the same as the right eigenvector of
R.
Consider further (US
-
R)ai = (miUai
-
bimi) =
0. Hence
U rotates the vector ai to the vector bi. More explicitly (in aik , the i is
the vector component and the k is the Cartesian index) which defines for our
purposes the rotation matrix (up to the det(U ) condition)
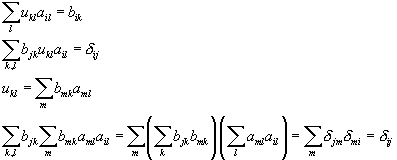
To compute D it is not
necessary to compute U
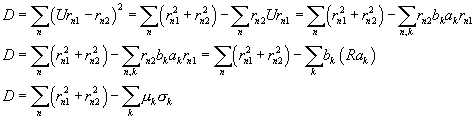
If the determinant of U is negative, sk (k is the index
of the smallest eigenvalue) is –1
Otherwise it is one.