Global optimization and smoothing of an energy function

Here we consider an example of potential smoothing. A “smoothing protocol” is defined by the following integral transform

where the parameter determines the extent of the smoothing. It covers a range from a value yielding a smooth surface to a value recovering the original surface.

Here is a one choice for the transformation on a one-dimensional potential (the algorithm is not limited to one dimensional cases)

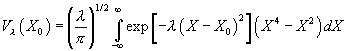
A useful change of variable is We have

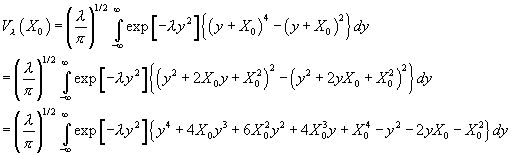
Note that powers that include only (no ) are irrelevant since after the integration they produce a constant that does not affect the dependence. Also odd powers in are integrated to zero. Therefore the only remaining terms are summarized below:

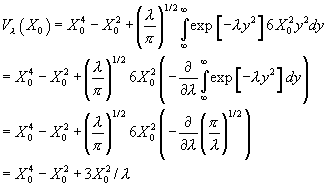
Note that is a critical value in the smoothing procedure. At values smaller than 3 there is only one minimum (but at the wrong position – exactly at the top of the barrier!), below the critical value the potential splits to the two minima. The distance between the two minima grows until at the limit of large value the original surface is recovered.