Monte-Carlo Sampling

 

Consider a system with an energy �that we wish to optimize (i.e. to find the coordinates of the global energy minimum -- ). One popular global optimizer is the Monte Carlo (Metropolis) procedure.

 

Let the current coordinate vector be . We sample at random a displacement �(�random� numbers and generation of pseudo-random numbers will be discussed separately). We then check if the (potentially) new coordinate �is better than the coordinate . The check is based on the energy difference, i.e. we compute

 

 

If �is smaller than zero then the step is accepted as our new coordinate set with probability 1. Hence a new coordinate set is assigned which is �

 

If �is greater than zero then the new coordinate is accepted with a probability which is exponentially small with the energy difference, , where �is the �temperature�. The higher is the temperature the more likely is the acceptance of a configuration with high energy. At the limit of infinite temperature all steps are accepted.

 

At the limit of zero temperature, only configurations that are going downhill in energy are accepted, in that case we have a rather poor local minimizer (compared to conjugate gradient).

Writing it all down more formally we define the conditional probability �that a move from �to �is accepted as the new configuration. This conditional probability is computed as follows (in the Metropolis algorithm)

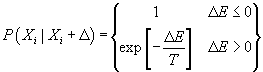
This condition is used to generate a sequence of coordinates of a significant length .� The set so defined is also a Markov chain. (A Markov chain is a set of sequential coordinates �where the creation of �in the sequence depends only on the coordinates �and not on previous coordinates e.g.

 

What can we say about the distribution of these points when N (the number of steps) is approaching infinity??

First, let as think conceptually on a large number of independent Markov chains. We start from different initial conditions and let the independent Markov chains develop independently. The collection of chains is denoted () where the index j is for Markov chain j and the index i is for the position along the chain. Below we refer to the index �i� as time.

Consider a specific �time� slice (specific index �i�). If we have many independent Markov chains we can histogram their current position �and discuss the frequency density to find the coordinate at a specific position at a specific time slice,.

An interesting special case is when the probability �does mot change during a single time step, i.e.� . No change in a single step implies that there is no way that this distribution will ever change. We denote this surprising probability by �(eq for equilibrium � i.e. no change).

An interesting result is that �is a trap! Once generated from another distribution there is no way out! It is a sort of a �black hole�, which with sufficiently large radius of attraction (the range of distributions that are attracted to ) will trap any initial distribution we may have. What is this probability?

Important comment: Suggesting that the distribution does not change does not mean that individual Markov chains do not change their coordinates at a specific time slice. They do. Only by averaging over a large number of alternative Markov chains we may reach the above equilibrium distribution.

At the assumed equilibrium probability we may have:

Hence, what we depleted from one coordinate �and moved to the other position �(left side) should be equal to the amount depleted from and moved in the reverse direction to . If this condition is met then the distribution is stationary (or at �equilibrium�).

Moving from side to side and using the Metropolis definition of the conditional probability we have

 

 

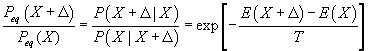
As the temperature becomes low we are sampling lower energy minima more significantly. If we start at high temperatures (in which all the coordinates are (roughly) equally probable and then reduce the temperature then we increase the probability of being at lower energy minima. Optimization with Monte Carlos is based on running Markov chain(s) at high temperatures and slowly reducing the temperature. The final result at the lowest temperature (if we can reach true equilibrium at each temperature) should be global energy minimum.

 

�