Conjugate gradient in linear algebra

The basic target function to solve is:

The gradient of the function

Starting from an initial point , we search (in the steepest descent spirit) for a minimum along the gradient direction at , that is

How to determine ?

It is determined by the requirement that at the new position, , the gradient of the function is normal to (hence that we minimized the function in the one dimensional search along )

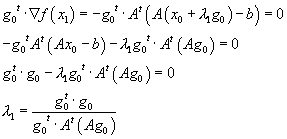
If we continue in exactly the same way (i.e. define ) then we are following the steepest descent algorithm. Instead we add now the new twist (condition) that along the new direction there will be no new build up of the -- we have where the direction and the scalar are not known. is chosen in such a way that there is no build-up of the gradient in the direction (for any ). This ensures that by the end of the day we are fully minimized in two directions and .

Note that the rate of change of the gradient in the problem at hand (quadratic problem) is a constant. This means that the condition we set will work anywhere along the new line of search. This condition is (however) only an approximation when functions more complex than a quadratic form are considered. Note also that if we continue along the new direction consists of then we do not develop gradient components along and .

Here is how we determine and

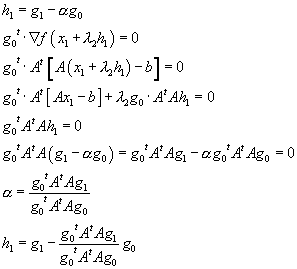
Once we determine the search direction we can compute . We require that along the new search direction , the gradient of the function will be minimized.

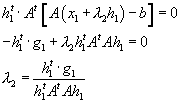
This process is repeated: e.g.

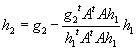
Another useful example of iterative procedure similar to this is

The determination of the largest eigenvalue:

For an arbitrary vector we have

where the s are the eigenvectors of the matrix

computing we have

enriching the largest eigenvalue. A process that can be repeated to desired accuracy.

How will you determine the lowest eigenvalue using CG?