COM S 321 LEC 01 12/17/2001 12:00 PM HO 110

The exam will include only four questions and will last 2.5 hours

1. Consider the following Newton equation: where the force is a constant. Does the integration of this equation of motion with the Euler algorithm conserve phase space volume?

2. Design an algorithm that uses uniform random numbers between zero and one and generates random numbers sampled from the probability density .

3. Design an algorithm that uses uniform random numbers between zero and one and generates random numbers sampled from the probability density , is a constant such that the probability density is integrated to one.

4. We wish to overlap protein structures of the same length against a single core protein structure. We assume that all the structures are already overlapped with respect to each other. Hence, we are only required to find a single rotation matrix to optimally overlap the set of shapes against the single core structure. (a) Write down the required constrained optimization formula using Lagrange multipliers. (b) By analogy to the problem we worked out in class suggests an algorithm that will address the above problem.

5. Design a Monte Carlo procedure that will optimize the alignment of two sequences and (including gaps) using a fixed constant penalty for the gap and a known substitution matrix , are the types of the amino acids.

6. is a positive definite matrix. Design a steepest descent algorithm to find its largest eigenvalue.

7. A Markov chain is computed using the following criterion:

A step is accepted with a probability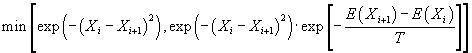

What is the equilibrium distribution?

8. It is possible to obtain mutations in cycles i.e. instead of we have , design a Dynamic Programming procedure for sequences that are related by cyclic transformations and with complexity of .