Regular expressions provide an expressive language for describing patterns. They are particularly useful because, like the simple string patterns we saw earlier, they can be efficiently searched for in a larger string. It turns out that for any regular expression, a deterministic finite automaton (DFA) can be constructed that recognizes any string that the regular expression describes in time linear in the length of the string! (For those who care about language: "automaton" is the singular, "automata" is the plural. It's the Greeks' fault.) A DFA, also known as a finite state machine, is a finite graph in which the vertices (nodes) are the states of the automaton. The edges of the graph are labeled with characters, and there is a distinguished start state and some number of accept states. In a deterministic finite automaton, there is at most one outgoing edge from any given node labeled with a particular character. The automaton starts in the start state and scans the text from left to right. For each input character, it follows the single outgoing edge from the current state that is labeled with that character. If the automaton is in the accept state, it has seen a string matching the pattern.
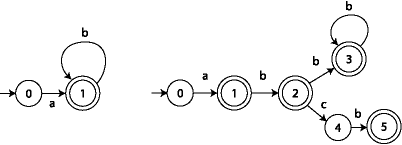
It is conventional to draw finite automata as a graph where the states are drawn as circles and the accept states are drawn as double circles. For example, an automaton that accepts the same strings as the regular expression ab* is shown on the left; the automaton on the right corresponds to the more complex regular expression a(b*|bcb); note that it has four accept states.

A DFA can be implemented very easily using a table. The table maps from the pair (current state, input character) to the next state of the automaton. For example, the automaton on the right can be written as this table:
a b c accept 0 1 - - F 1 - 2 - T 2 - 3 4 T 3 - 3 - T 4 - 5 - F 5 - - - T
Implementing pattern matching for regular expressions using a finite automaton is thus quite simple:
type state = int (* Note: 0 is the start state *) datatype dest = State of state (* Edge destination is another state *) | Error (* if no next state *) type DFA = {table: dest Array2.array, accept: bool Array.array} (* Check whether the DFA "pattern" accepts "text" *) fun search({table, accept}: DFA, text: string): bool = let (* Give the next state of the DFA, assuming that it is in * state "state" and the next character is text[pos]. *) fun next_state(pos: int, state: int): dest = if pos = String.size(text) then EOF else let val char = Char.ord(String.sub(text, pos)) in Array2.sub(table, state, char) end (* Walk the DFA down the string "text" from position "pos", * returning whether it accepts the rest of the string. *) fun search1(pos: int, state: int): bool = if pos = String.size(text) then Array.sub(accept,state) else case next_state(pos, state) of Error => false | State(s) => search1(pos+1, s) in search1(0,0) end
The run time of this loop is clearly O(n) in the length of the text
string, which makes it asymptotically similar in run time to the simple
string matching algorithms we saw earlier! Note that this code simply checks
whether the entire text matches the regular expression, but we can easily
build a regular expression that allows the given regular expression to
occur anywhere inside the string. Given a regular expression A, the
expression .*A.* describes any string
that contains A! This does beg the question
of how much time is needed to construct the finite automaton. In
CS381/481 you'll learn how to efficiently construct finite automata
from regular expressions. It turns out that the SML/NJ library includes a
functor RegexpFn that provides the functionality for you.
Here is another implementation of regular-expression pattern matching that is not based on finite automata.
The following datatype definition defines the abstract syntax for regular expressions, which is our internal representation of patterns.
datatype regexp =
None (* matches no string *)
| Empty (* matches the empty string *)
| Char of char (* Char(c) matches a string "c'" iff c = c' *)
| AnyChar (* AnyChar matches a string "c" for any c *)
| Or of regexp * regexp (* Or(r1,r2) matches s iff r1 matches s or r2
matches s *)
| Concat of regexp * regexp (* Concat(r1,r2) matches s iff we can break
s into two pieces s1 and s2 such that r1
matches s1 and r2 matches s2. *)
| Star of regexp (* Star(r) matches s iff
Or(Empty,Concat(r,Star(r))) matches s.
That is, if zero or more copies of r
concatenated together matches s. *)
The parser converts a string representing a pattern (e.g. "a*.b") to our internal representation (e.g.
(* raised when we encounter a syntax error *)
exception SyntaxError of string
(* tokens processed by the parser *)
datatype token =
AtSign | Literal of char | Pipe |
Percent | Asterisk | LParen | RParen | Period
(* raised when we don't recognize a token *)
exception LexicalError
(* convert list of characters into a list of tokens *)
fun tokenize (inp : char list) =
(case inp of
nil => nil
| (#"|" :: cs) => (Pipe :: tokenize cs)
| (#"%" :: cs) => (Percent :: tokenize cs)
| (#"." :: cs) => (Period :: tokenize cs)
| (#"*" :: cs) => (Asterisk :: tokenize cs)
| (#"(" :: cs) => (LParen :: tokenize cs)
| (#")" :: cs) => (RParen :: tokenize cs)
| (#"@" :: cs) => (AtSign :: tokenize cs)
| (#" " :: cs) => tokenize cs
| (c :: cs) => Literal c :: tokenize cs)
(* parsing functions that map lists of characters to regular expressions *)
fun parse_exp ts =
let val (r, ts') = parse_term ts
in
case ts' of
(Pipe::ts'') =>
let val (r', ts''') = parse_exp ts''
in
(Or (r, r'), ts''')
end
| _ => (r, ts')
end
and parse_term ts =
let val (r, ts') = parse_factor ts
in
case ts' of
((AtSign | Percent | Period | Literal _ | LParen)::ts) =>
let val (r', ts'') = parse_term ts'
in
(Concat (r, r'), ts'')
end
| _ => (r, ts')
end
and parse_factor ts =
let val (r, ts') = parse_atom ts
in
case ts' of
(Asterisk :: ts'') => (Star r, ts'')
| _ => (r, ts')
end
and parse_atom nil = raise SyntaxError ("Factor expected\n")
| parse_atom (AtSign :: ts) = (None, ts)
| parse_atom (Period :: ts) = (AnyChar, ts)
| parse_atom (Percent :: ts) = (Empty, ts)
| parse_atom ((Literal c) :: ts) = (Char c, ts)
| parse_atom (LParen :: ts) =
let val (r, ts') = parse_exp ts
in
case ts' of
(RParen :: ts'') => (r, ts'')
| _ => raise SyntaxError ("Right-parenthesis expected\n")
end
| parse_atom _ = raise SyntaxError "Not an atom"
fun parse s =
let val (r, ts) = parse_exp (tokenize (String.explode s))
in
case ts of
nil => r
| _ => raise SyntaxError "Unexpected input.\n"
end
handle LexicalError => raise SyntaxError "Illegal input.\n"
The main pattern matching engine is match_is. It tries to match a given regular expression against a given string, where we represent the string as a list of characters. The inputs to match_is are a regular expression r, a list of characters cs, and a continuation k. We want match_is to return true iff cs can be broken into two lists of characters cs1 and cs2 such that r matches cs1 and k(cs2) returns true. The continuation k is used to deal with concatenation so that we don't have to worry about guessing how to split up a string.
fun match_is None cs k = false
| match_is Empty cs k = k cs
| match_is (Char c) [] _ = false
| match_is (Char c) (c'::cs) k = (c=c') andalso (k cs)
| match_is AnyChar [] _ = false
| match_is AnyChar (_::cs) k = k cs
| match_is (Or(r1,r2)) cs k =
match_is r1 cs k orelse match_is r2 cs k
| match_is (Concat(r1,r2)) cs k =
match_is r1 cs (fn cs' => match_is r2 cs' k)
| match_is (r as Star r1) cs k =
k cs orelse match_is r1 cs (fn cs' => match_is r cs' k)
We can try to prove the code is correct by induction on the length of the input list of characters cs, but this will fail since not all recursive calls to match_is cause the list to get smaller (notably the Or and Star cases). We can also try to prove the code correct by induction on the structure of a regular expression, but this will also fail since the regular expression doesn't always get smaller in a recursive call (notably in the Star case). So we can try to prove the code is correct by using a metric where either (a) the size of the regular expression goes down, or else (b) the length of the input string goes down. Unfortunately, such a proof also fails in the case of Star. The reason is that for the pattern Star Empty, a non-empty list cs = c::rest, and k = null, we have:
(k c::rest) orelse match_is Empty (c::rest) (fn cs' => match_is r cs' k) = false orelse match_is Empty (c::rest) (fn cs' => match_is r cs' k) = match_is Empty (c::rest) (fn cs' => match_is r cs' k) = match_is r (c::rest) k
so we end up calling match_is recursively with the same regular expression r = Star Empty, the same list of characters cs = c::rest, and the same continuation k = null. Thus, our induction hypothesis will not apply and it becomes clear that the code really has a bug in it. In particular, if we call match_is (Star Empty) [#"a"] k, then the code will loop forever!
Here is a way around this problem. We define a pair of mutually recursive functions match_nz and match_z. The function match_nz is like match_is, except it will only succeed if at least one character of cs is matched, ensuring that the continuation always gets a smaller string. The function match_z will only match the empty string, or else call match_nz.
fun match_nz None cs k = false
| match_nz Empty cs k = false
| match_nz _ [] k = false
| match_nz (Char c) (c'::cs) k = c=c' andalso k cs
| match_nz AnyChar (_::cs) k = k cs
| match_nz (Or(r1,r2)) cs k =
match_nz r1 cs k orelse match_nz r2 cs k
| match_nz (Concat(r1,r2)) cs k =
match_nz r1 cs (fn cs' => match_z r2 cs' k) orelse
(match_z r1 [] null andalso match_nz r2 cs k)
| match_nz (r as Star r1) cs k =
match_nz r1 cs (fn cs' => match_z r cs' k)
(* either cs = [] and r matches [] or match_nz r cs k *)
and match_z None [] k = false
| match_z Empty [] k = k []
| match_z (Char c) [] k = false
| match_z AnyChar [] k = false
| match_z (Or(r1,r2)) [] k =
(match_z r1 [] k) orelse (match_z r2 [] k)
| match_z (Concat(r1,r2)) [] k =
match_z r1 [] (fn cs' => match_z r2 [] k)
| match_z (r as Star r1) [] k = k []
| match_z (r as Star r1) cs k = match_nz r cs k orelse k cs
(* in every other case we must match a nonnull prefix of cs *)
| match_z r cs k = match_nz r cs k
We start off the whole process by calling match_z with an initial continuation that returns true iff the list has been entirely consumed.
fun match regexp string = match_z regexp (String.explode string) null fun matches (regexp: string) (string: string) : bool = match (parse regexp) string