We now look at two issues in code verification that we've ignored till now: the issues of nontermination and of data abstraction.
Our approach to proving the correctness of programs has been to show that each function obeys its spec assuming that any function calls that happen inside the function obey their specs. However, this doesn't work as nicely as we might expect in the presence of recursion. For example, consider the following two implementations of a list length function:
fun length(lst) =
case lst of
[] => 0
| _::t => 1 + length(t)
|
fun length(lst) =
length(lst)
|
Clearly, the implementation on the right is not going to work; it's going
to go into an infinite loop. Yet according to our recipe for verification,
this function is correct–it just calls the function length,
which we're supposed to assume obeys its spec. So in what sense is this
implementation correct? It's what is called partial correctness.
A program is partially correct if whenever it terminates (finishes evaluating), it produces results in accordance with the specification. However, there is no guarantee that it terminates. To put it another way, a partially correct program either fails to terminate or it produces the correct results. If we can show that a partially correct program also terminates, then the program is totally correct: it will always satisfy the spec.
It is possible to extend our vc function to generate preconditions for total correctness, but for most SML code, this is overkill, because it is typically easy to reason about termination in functional programming languages.
The key to proving that a recursive function terminates is to show that the argument to the recursive function gets strictly smaller in some sense whenever there is a recursive call. And further, that the argument cannot keep getting smaller indefinitely. For example, if the argument is always a nonnegative integer, and the recursive call is always to a smaller nonnegative integer, then the recursion must bottom out at some point (at or before zero). This is why we know that the implementation of factorial terminates:
(* Requires: n≥0 * Returns: fact(n) = n! *) fun fact(n) = if n = 0 then 1 else n*fact(n-1)
We can see that the recursive call is to a smaller n, and only if n≥1,
so the value of n passed is always at least zero. You are likely to recognize
this kind of argument as an argument by induction. We can see that fact
terminates in the case where n=0, and assuming it terminates for n-1, it also
terminates for n. Therefore it terminates for all n≥0.
In general the function argument we base this inductive reasoning on is
something other than an integer. Commonly we call recursive functions on
recursive datatypes, such as lists. In the case of the (good)
length function defined earlier, the recursive call is to
t, which is a smaller list than lst. And lists
cannot keep getting smaller indefinitely. So length terminates,
by induction on the length of the list.
Lists are just one example of a datatype. In general, suppose we have
datatype t = X1 of t1 | ... | Xn of
tn. A function will always terminate if it that matches an argument
of type t, and calls itself recursively only on values extracted
from the pattern-match, of types t1...tn (or pieces of
those values). The reason is that the original argument is built up by using
datatype constructors. If we write out the value of the original argument using
these datatype constructors, there is some maximum depth of nested parentheses
in the value. This parenthesis depth must be smaller in the values produced by
pattern matching, because the outer datatype constructor (one of the
Xi) is removed by pattern matching. Since the parenthesis depth must
be at least zero, the recursion must terminate.
This points out a nice property of functional programming languages. In a language like Java or C, we can construct similar data structures using references (pointers). But there is nothing in those languages ensuring that when pointers are followed, the value obtained is smaller in some sense. So reasoning about termination is a bit harder in languages without algebraic datatypes.
We've seen how to prove that a function satisfies its specification. In general, we have a function f with a precondition pre(f) and a postcondition post(f). If the function is defined as fun f(x) = e, then we need to show that if the precondition is true, then the postcondition must be true once e is finished evaluating. We also saw that we could define a function vc() that could be used to convert e and post(f) into a precondition. Then we could just prove the formula pre(f)⇒vc(e, r, post(f)) to show that f is implemented correctly.
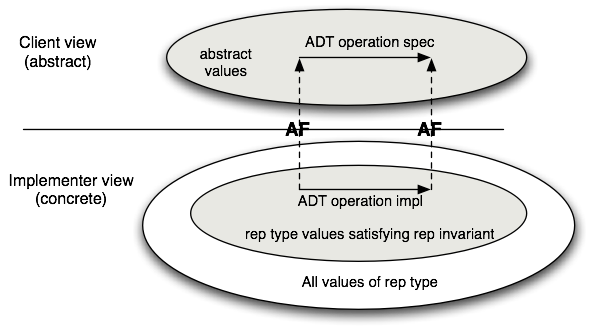
What about checking the correctness of an operation f that is part of a data abstraction t? There is a problem: the specification of f is in terms of the abstract type t, but the actual code is in terms of the concrete type for t. Also, the argument for correctness of f in general depends on the representation invariant for t, which doesn't show up in the spec. Our goal is to take the abstraction precondition and postcondition, the abstraction function AF, and the rep invariant RI, and derive a concrete precondition and postcondition PRE and POST that allow us to show the code is correct by proving PRE⇒vc(e, r, POST).
As a simple example, suppose we didn't have a boolean type in our language and we needed to implement it. Here is a potential signature:
signature BOOL = sig (* A boolean is either true (⊤) or false (⊥) *) type bool val true: bool val false: bool (* not(x) = ¬x *) val not: bool -> bool (* or(x,y) = x ∨ y *) val or: bool * bool -> bool (* and(x,y) = x ∧ y *) val and: bool * bool -> bool (* if_(b,x,y) = x if b is true, y otherwise val if_: bool * 'a * 'a -> 'a end
Here's a slightly curious implementation using
ints:
structure IntBool :> BOOL = struct
type bool = int
(* RI(x) is -10 ≤ x ≤ 10
AF(x) is true (T) if x ≥ 0, false (⊥) if x < 0.
*)
val false = 0
val true = 3
fun not (x: bool) = 1 - x
fun and (x:bool,y:bool) = if x > y then y else x
fun or (x:bool,y:bool) = if x < y then x else y
fun if (c:bool, e1:'a, e2:'a) =
if c ≥ 0 then e1 else e2
end
Does this really work? Close, not quite. If we try to prove that this code is correct, we will find some bugs.
Recall that a data abstraction operation is correct if its implementation
satisfies a commutation diagram:

Consider what we need to show to see whether and is implemented
correctly. When the function is called, we get to assume that the rep invariant
holds on the arguments: RI(x)∧RI(y), and also that the precondition of the
function (in this, just ⊤) holds. Using this assumption, we need to show
that the function obeys its spec. Calling the result of the function r, we need
AF(r) = AF(x)∧AF(y). And we need to show that the rep invariant holds on the
result: RI(r). So we are showing the correction of the function code with
respect to a precondition PRE that is RI(x)∧RI(y), and a
postcondition POST that is AF(r)=(AF(x)∧AF(y)) ∧ RI(r). Using the
concrete precondition PRE and postcondition POST, the implementation
is correct if PRE⇒vc(e, POST).
We can derive concrete preconditions and postconditions mechanically from the specification of the function. In general, for a function f, we construct them by mapping specification variables through the abstraction function, and adding the rep invariant to both sides:
| PRE | = | pre(f){AF(arg(f))/arg(f)} ∧ RI(arg) |
| POST | = | post{f}{AF(arg(f))/arg(f), AF(result(f))/result(f)} ∧ RI(result(f)) |
Let's try this out on the Bool structure, and look at just
the operations and and not. We'll reason a bit
informally about the code, but the reasoning steps we take exactly correspond
to what we'd see if we constructed a formal proof of the formula PRE⇒vc(e, POST).
A typical way to construct a good informal argument is to think about
the possible evaluations. The body of and is an if,
which can either go to the then clause or to the else
clause. Let's consider each possibility.
| AF(x), AF(y)= | ⊥, ⊥ | Since y<0, AF(r) = ⊥ |
| AF(x), AF(y)= | ⊥, T | Since x>y, x<0, y≥0, this can't happen. Vacuously satisfied. |
| AF(x), AF(y)= | T, ⊥ | Since y<0, AF(r) = ⊥ |
| AF(x), AF(y)= | T, T | Since y≥0, AF(r) = T |
Let's try also verifying not. PRE is -10≤x≤10, and
POST is -10≤r≤10 ∧ AF(r) = ¬AF(x). The code computes r as 1-x. So
the code is correct if the following formula is true:
-10≤x≤10 ⇒ -10≤1-x≤10 ∧ (1-x ≥ 0 ⇔ x < 0). Unfortunately neither
of the conjuncts on the right-hand side is implied by the left-hand side.
If x = -10, then 1-x = 11, and the left conjunct (-10≤1-x≤10) fails.
If x is 1 or 0, then the right conjunct (1-x ≥ 0 ⇔ x < 0) fails.
We can fix the implementation by changing the abstraction function and
rep invariant as follows:
(* RI(x) is -9 ≤ x ≤ 10
AF(x) is true (T) if x > 0, false (⊥) if x ≤ 0.
*)
The implementation of if also needs to be fixed
to match the new abstraction function:
fun if (c:bool, e1:'a, e2:'a) =
if c > 0 then e1 else e2
This example shows that by carefully (yet informally) reasoning about code using the abstraction function and rep invariant, we can catch subtle bugs. The key is to use the AF and RI to convert the function specification into a concrete specification that we can then use to argue that the implementation works.
We could have done the same example more formally using natural deduction, and the same key reasoning steps would have shown up. Doing a formal proof is usually not worth it, but it's useful to understand how the informal arguments we should be doing when writing code map down to a more precise formal system. Good programmers do reasoning equivalent to that above when they write code, sometimes without realizing it!