For this problem set, you are to turn in an overview document covering problems 3 and 4. The overview document should be composed as described in Overview Requirements. You should read this document carefully. In particular, starting with this problem set, it's your job to convince us that your code works, by describing your implementation and by presenting a testing strategy, test cases, and results. We have provided an example overview document written as if for Problem Set 2.
You may work on this problem set with a partner. We strongly recommend discussing, critiquing, and agreeing on specifications for Parts 3 and 4 before doing any implementation. A nice approach is to have one partner write rough drafts of specs for Part 3, the other partner write rough drafts of specs for Part 4, then to discuss how both specs can be improved. You can also bring specs to office hours to get feedback. When critiquing a spec, think about the spec both from the standpoint of the client who is going to use the spec, and the implementer who must implement it. It is also a good idea to discuss and agree on the abstraction function and rep invariant for your data structures.
Look for changes to the problem set highlighted in red.
Feb 23: We have provided an example overview document written for PS2 (even though we didn't ask you to write an overview document for that problem set.
Feb 17: We have provided a function GreatCircle.distance that
computes great-circle distance, for use in Part 4. So you don't need to do any
geometry to compute distances. You should use this instead of the
Spherical module initially provided.
Consider four functions:
fun twice f x = f (f x)
fun thrice f x = f (f (f x))
fun inc i = i + 1
fun applyManyTimes f n m q =
case (n,m) of
(0,0) => q
| (_,0) => twice f (applyManyTimes f (n-1) m q)
| _ => thrice f (applyManyTimes f n (m-1) q)
Describe the behavior of applyManyTimes inc n m q
as a mathematical function of n, m, and q. Using the substitution model,
show the evaulation of applyManyTimes inc 3 1 2.
Consider the following function specifications for functions
a–g of type
int list->int*int
. Draw a
Hasse diagram showing
which function specifications refine each other. This diagram should include
a node for each function name. If function spec A refines spec B, the name B
should appear higher in the diagram. Further, there should be a line in the diagram
connecting A and B, unless there is some third spec C where A refines C and C
refines B.
(* a(x) is a pair (y,z) where y is the smallest element in x and z is
the largest.
Requires: x is non-empty. *)
(* b(x) = (y,z), where y is the smallest element of x, and z is the largest.
Requires: x is nonempty and in ascending sorted order. *)
(* c(x) is a pair (y,z) where y and z are elements in x.
Requires: x contains at least two nonequal elements. *)
(* d(x) = (y,z), where x=[y,z].
Requires: x is a two-element list. *)
(* e(x) = (y,z), where y is the first element of x, and z is the last.
Requires: x contains at least two elements. *)
(* f(x) is a pair (y,z) where y is the smallest element in x, z is
the largest, and y≠z.
Requires: x contains at least two nonequal elements. *)
(* g(x) is a pair (y,z) where y is an element in x and y < z.
Requires: x contains at least three nonequal elements and is in
ascending sorted order. *)
Hint: E refines C, so E should be below C in the diagram and connected to it (perhaps indirectly). On the other hand, G and C have no refinement relationship, meaning that G does not refine C, and C does not refine G.
Several algorithms, including some compression and string matching
algorithms, make use of dictionaries whose keys are strings. Here, a string
is a sequence
of elements of a given type, and that type is
called an alphabet. In this problem, keys
have the SML type string, which is a string over the
alphabet char.
A trie, or prefix tree, is an efficient data structure for implementing this kind of dictionary (“trie” is pronounced “try”). A trie is a tree in which there is one node for every common string prefix, and every node potentially represents a mapping from a string to a value. Each edge is labeled with an element of the alphabet, so each node can have up to N children, where N is the size of the alphabet. A node n corresponds to a string s exactly when the sequence of elements traversed on the path from the root to n is the string s. To represent a mapping from string s to value v, written s→v, a trie stores v in the node corresponding to s. When a trie maps s to v, we say that v is bound to s. Two advantages of this data structure are that it represents common string prefixes in a space-efficient manner, and that insertions and retrievals are achieved using time-efficient searches starting from the root.
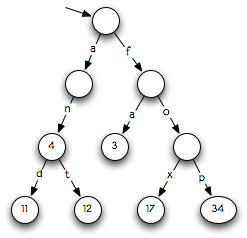
Suppose we want to build a dictionary from strings to integers. In this case, edges are labeled with characters, and integers are stored in some of the nodes. Here is an example:
This trie describes the dictionary
{"an"→4, "and"→11, "ant"→12, "fa"→3,
"fox"→17, "fop"→34}.
The integers shown are stored in the adjacent nodes. Note that nodes might not
have values. For example, the node that corresponds to string
"a" doesn't have a value. Hence, "a" is not in the
dictionary.
Your task is to complete the following:
TRIE. The existing
specifications may be incomplete, incorrect, or nonexistent.
type 'a trie = (* your implementation here *)
repOK. If the input trie
satisfies the representation invariant, then repOK
simply returns the input trie. Otherwise, repOK
raises Fail.empty
value, representing an empty trie. Then implement the functions
put and get.
The put function adds a
mapping to a trie. If the key already exists in the trie, its
binding is updated. The function get returns the
binding of a string in the trie. If the string does not exist in the
trie, then a NotFound exception must be raised.
val empty: 'a trie val put: 'a trie * string * 'a -> 'a trie val get: 'a trie * string -> 'a
Note: The course staff will use these functions to generate the inputs for testing your other functions. Therefore, be careful to implement them correctly.
size returns the
number of mappings in a trie. Computing the size of the trie must be
an O(1) operation. Function
tabulate(n,f) creates a new
trie with n mappings, where mapping k is
f(k), for k between 0 and
n-1, inclusive. Function fold f v t
performs folding over
trie t, starting with initial accumulator value
v, applying function
f at each step. A fold
must visit key–value mappings in lexicographic (dictionary)
order on the keys.
val size: 'a trie -> int val tabulate: int * (int -> string * 'a) -> 'a trie val fold: (string * 'a * 'b -> 'b) -> 'b -> 'a trie -> 'b
sort: string list
-> string list that sorts a list of strings using a trie.
The returned list must be sorted in ascending lexicographic order. The
algorithm must have O(n) complexity,
where n is the sum of the lengths of all strings.
A quadtree is a data structure that supports searching for objects located in a two-dimensional space. To avoid spending storage space on empty regions, quadtrees adaptively divide 2D space. Quadtrees are heavily used in graphics and simulation applications for such tasks as quickly finding all objects near a given location, and for detecting collisions between two objects.
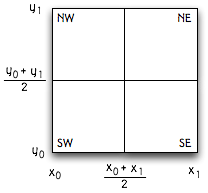
There are many variations on quadtrees, specialized for different applications. For this problem set, we'll implement a variation in which a quadtree represents a rectangular region of space parameterized by x and y coordinates: all the space between x coordinates x0 and x1, and between y coordinates y0 and y1. A leaf node contains some (possibly empty) set of objects. A non-leaf node has four children, each covering one quarter of the original space, as shown in this picture:
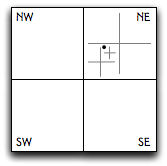
To find an object near coordinates (x,y), a quadtree is traversed starting from the top node and walking down through the appropriate sequence of child nodes that contain the point (x,y) until a leaf node is reached. The object or set of objects at the leaf can then be tested against. This figure depicts the quadtree nodes visited as the object at the black dot is searched for:
Design and implement a quadtree data structure. Choose the operations carefully; you should keep the next part in mind while doing this, but also try to provide an abstraction that will be useful to other clients. Be sure to write clear specifications of all operations and to document the abstraction function and representation invariant.
Hint: We are being deliberately vague about some details of the data structure: for example, how many objects are stored at leaf nodes. Some versions of quadtrees even store objects at non-leaf nodes. Think carefully about (and justify) the data structure you design.
We have provided a text file containing the latitude and longitude of over 170,000 populated cities and towns in the United States. Write a program that uses your quadtree data structure to answer queries of the form, “What cities are within N miles of a given latitude and longitude?” Your program should provide a top-level function that implements this functionality, with the following signature:
nearbyCities : real * real * real -> string listFor example, calling
nearbyCities(20.0, 42.4406, -76.4966)
should return a list of the names of the cities within 20 miles
of Ithaca, NY.
Measure and report how long it takes your program to
answer a million such queries targeted at one of the cities on the list,
randomly chosen for each query, and using a constant distance of 20 miles.
(Hint: store the city data in a vector so a random city
coordinate can be obtained in constant time.)
We will give a small bonus and bragging rights to the best (i.e, fastest
and correct) implementation.
Computing distances is complicated by the fact that they are actually located on the curved surface of the earth. For the purposes of this assignment, we will assume that the earth is a sphere with a radius 3963 miles, and that cities are located at sea level. We have provided the following useful function for computing distances between two points on the earth:
You still will have to think about how to use a quadtree to find points lying within a circle. (Hint: can you bound the great-circle distance to all points within a quadtree cell?)